共轭梯度算法在振动信号处理中的应用

李琪琪，庄 建，王智超，张国庆

(北京航天试验技术研究所，北京 100074)

0 引言

在液体火箭发动机试验过程中，当出现异常频率振动时，由于能量集中，很容易使发动机破坏，如出现在涡轮泵转动频率附近的“次同步”振动，可在十分之几秒内使涡轮泵轴承毁坏[1]。可见，发动机试验振动参数的测量及数据的有效分析对于保证发动机不受损坏，预防试验破坏性具有一定的意义[2]。

目前液体火箭发动机试验振动信号的处理、分析主要在频域进行[3]，分析多用傅里叶变换的谱估计方法[1]，这种方法有着分辨率低和旁瓣泄漏严重的固有缺点，严重时会将振动信号中包含的主要频率特征掩盖，而产生较大的失真。而现代谱估计方法可以有效地解决这个问题，现代谱的精确估计值可以当作是解一组线性方程，AR(auto—regressive)、MA和ARMA是功率谱中的主要参数模型。AR参数模型谱估计是现代谱估计中最常用的时间序列的建模方法，目前已广泛应用于很多领域，如雷达、声纳、机械等。

在每种模型的建立中，其核心问题是其参数的求解问题。在本文中用共轭梯度算法以及线性预测的知识来求解参数，实现功率谱估计[4]。共轭梯度法是一种具有低计算复杂度和高计算效率的参数计算方法[5]。

对基于共轭梯度和AR模型的谱估计算法进行了实验数据仿真分析，并用试验数据进行了验证。与传统的经典谱估计算法相比，本文的算法具有更好的分辨率。

1 基于共轭梯度和AR模型的谱估计算法

1.1 AR模型概述

对于一个AR模型，其中输入是白噪声u(n)，输出是x(n)，可表述为[6-9]

(1)

(2)

一个p阶的AR模型共有p+1个参数，即σ2和a1,a2,…，ap。AR模型参数的估计是通过求解自相关矩阵方程得到的[10]，本论文中将共轭梯度算法和线性预测的算法应用到AR模型谱估计中，得到参数后将其代入式(2)即可得到x(n)的功率谱。

1.2 共轭梯度算法

共轭梯度算法的迭代公式如下[11-12]。

(3)

w(n)=w(n-1)+α(n)p(n)

(4)

(5)

(6)

p(n+1)=g(n)+β(n)p(n)

(7)

式中：x(n)为信号输入量；R(n)为输入信号x(n)的自相关矩阵。式(3)～式(7)中，初始条件为w(0)=0,g(0)=b(0),b(0)=1,p(1)=g(0)，λf=0.999 9，η=0.999，M=70，M=p，N=1 024。在求解过程中设初值如下R(0)为一个N×N的0阵；g(0),b(0),p(1)为M×N的全1阵，最后通过迭代求出w(n)，即式(2)中的p个参数a1,a2,…,ap。

1.3 线性预测算法

一个p阶的AR模型和一个p阶的线性预测器是等效的。线性预测器误差能量的均值记为l，p阶预测器对输入x(n)预测的最小均方误差lmin为[13-14]

(8)

对同一平稳随机信号x(n)，因为其自相关函数是相同的，所以有

(9)

这样便用线性预测的算法求出了AR模型激励白噪声方差σ2，再由共轭梯度算法式(3)～式(7)求出p个参数ak，将这p+1个参数代入式(2)中即实现了信号x(n)的功率谱估计。

2 MATLAB算法仿真

2.1 仿真方案与条件

利用MATLAB仿真标准正弦信号，并加入白噪声干扰信号。分别用经典谱估计算法中的直接法和基于共轭梯度和AR模型的谱估计算法对仿真的标准信号进行功率谱估计仿真分析。这样，在知道被测信号的频率特性的前提下，分别用不同的功率谱估计算法对信号进行频率特性分析，通过仿真结果可以验证两种谱估计方法的性能[15-18]。

仿真条件1：设信号采样率为25 kHz，信号为主频为2 kHz和4 kHz的标准正弦信号叠加，并加入白噪声。在信噪比(SNR)为10 dB的条件下对两种算法进行仿真分析比较，算法仿真如图1和图2所示。可以看出，在信噪比SNR=10 dB的情况下，基于共轭梯度和AR模型的谱估计算法估计出的功率谱曲线要比经典法估计出的曲线平滑得多，后者谱线更清晰，分辨率优于前者，能更好地显示信号频率特性。

图1 SNR=10 dB，标准信号经典功率谱估计算法Fig.1 SNR=10 dB,classical power spectral estimation algorithm for standard signals

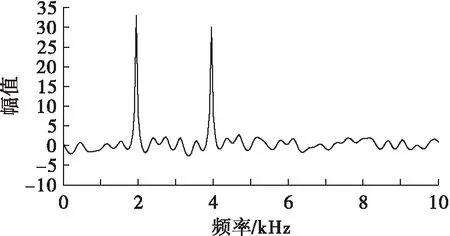
图2 SNR=10 dB，标准信号基于共轭梯度和AR模型的谱估计算法Fig.2 SNR=10 dB,spectral estimation algorithm based on conjugate gradient and AR model for standard signals

仿真条件2：设信号采样率为25 kHz，信号为主频为2 kHz和4 kHz的标准正弦信号叠加，并加入白噪声。在信噪比为—10 dB的条件下对两种谱估计算法进行仿真分析比较，算法仿真如图3和图4所示。可以看出，在信噪比SNR=—10 dB的情况下，基于共轭梯度和AR模型的谱估计算法可以清楚地分辨出信号的主频特性，谱线也要比经典法平滑得多。经典功率谱估计方法已经不能有效地分辨出信号的主频特性。可见，在低信噪比的情况下，本文的算法仍然保持了较好性能，明显优于经典谱估计方法。

图3 SNR=—10 dB，标准信号经典功率谱估算法Fig.3 SNR=—10 dB,classical power spectral estimation algorithm for standard signal

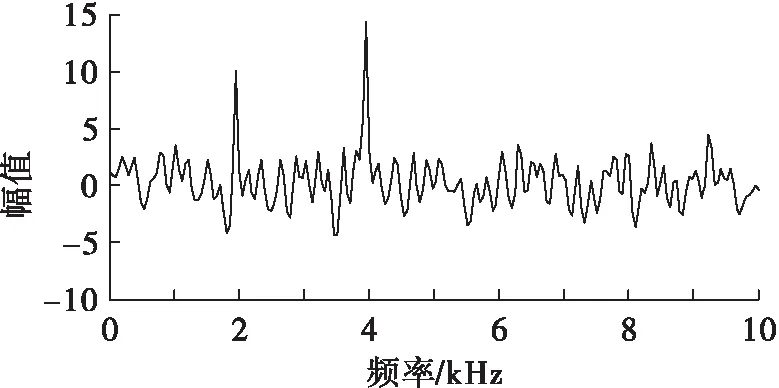
图4 SNR=10 dB，标准信号基于共轭梯度和AR模型的谱估计算法Fig.4 SNR=—10 dB,spectral estimation algorithm based on conjugate gradient and AR model for standard signal

2.2 试验数据验证

对液氧甲烷发动机第XX次试验中氢泵轴向振动信号进行频率特性分析，分析结果如图5和图6所示。从仿真结果可以看出，图6的基于共轭梯度算法和AR模型谱估计方法估计的功率谱曲线要比图5经典法估计出的功率谱分辨率好，能较好地反映振动信号的频率特征，谱线也平滑很多。

图5 试验信号经典功率谱估算法Fig.5 Classical power spectral estimation algorithm for test signals

图6 试验信号基于共轭梯度和AR模型的谱估计算法Fig.6 Spectral estimation algorithm based on conjugate gradient and AR model for test signals

3 结论

液体火箭发动机的结构特性是通过振动信号测量处理和分析得到的，本文将共轭梯度算法和AR模型的谱估计算法应用于液体火箭发动机试验的振动信号处理中[19]，对算法进行了仿真分析并与传统的经典功率谱估计算法进行了性能比较。仿真结果表明：AR模型的分辨率和随机信号x(n)的信噪比有着密切的关系，随着信噪比的降低，算法性能会下降，但要明显优于传统的谱估计算法。在信噪比为-10 dB的仿真环境下，经典谱估计方法已经不能有效分辨信号的频率特征，而基于共轭梯度和AR模型谱估计算法仍能较好地分辨出已知信号的特征频率，算法性能好。经典功率谱估计的分辨率反比于有效信号的长度，但现代谱估计的分辨率可以不受此限制[20]。在实际试验信号处理中，基于共轭梯度和AR模型谱估计算法的谱线依然具有较好的分辨率和平滑性。