玻璃纤维增强环氧树脂低温收缩应变的计算模型及应用
2021-03-01孙静
孙 静
(辽宁对外经贸学院,辽宁 大连 116052)
玻璃纤维增强塑料是以环氧树脂、不饱和聚酯、酚醛树脂为基体材料的复合材料[1],因其性能独特,在铁路、航空、家居、装饰建筑、环卫工程、建材卫浴等行业应用广泛[2-4]。玻璃纤维增强塑料分为碳纤维增强复合塑料、玻璃纤维增强复合塑料、硼纤维增强复合塑料等。纤维直径一般不大于10 μm,且耐化学药品腐蚀性较差,易发生断裂,但其具有韧性材料的特征,同时也具备黏弹性和弹塑性特征。玻璃纤维增强塑料相对密度为1.5~2.0,是碳钢密度的1/4~1/5,但其拉伸强度与碳钢接近甚至更高[5]。
塑料易被软化和分解,在外界环境中容易燃烧或发生老化等,限制了其应用[6-7]。因此,需要提高塑料的耐热性和热稳定性[8]。塑料的负荷变形温度较低,而力学性能会随温度的变化而发生显著变化,其与玻璃纤维的热膨胀系数差别较大,改变环境温度将直接影响基体材料与纤维的结合过程,进一步影响其力学性能[9]。Bagrets等[10]研究了影响短玻璃纤维增强聚酰胺(PA)66性能的因素,发现当温度和应变率保持不变时,增加纤维含量,复合材料的拉伸强度和弹性模量均显著增强。Takao等[11]研究了玻璃纤维质量分数为35%的玻璃纤维增强PA 66在室温条件下的疲劳寿命和循环加载频率,确定了其疲劳寿命。Zhou Yuanxin等[12]研究了应变率对短玻璃纤维质量分数为33%的短玻璃纤维增强PA 66的弹性模量与拉伸强度的影响,发现随着应变率的增加,复合材料的拉伸强度和弹性模量增加;复合材料的收缩率是决定其性能的关键参数。一般情况下,低温条件下玻璃纤维增强环氧树脂(GFEP)的收缩率数量级为10-3。GFEP具有热导率低、电绝缘性优良、密度小等优点,广泛应用于社会各领域。GFEP是一种各向异性材料,降低温度,不同方向的收缩率将会表现出差异,进而造成材料的扭曲变形,降低整体强度。GFEP收缩率的影响因素较多,很难通过计算得到。本工作设计了GFEP在低温条件下的收缩应变计算模型,并研究其算法的应用。
1 实验部分
1.1 主要原料
GFEP,淮南金德实业有限公司纤维钢筋分公司。
1.2 主要仪器与设备
Instron5989型万能拉力试验机,美国英斯特朗公司。
1.3 拉伸实验步骤
在万能拉力试验机上进行拉伸实验。低温拉伸的方向为0°和90°,采样频率为10 Hz,加载速度为1 mm/min,对试件进行拉伸,直到试件拉伸破坏。完成实验后,通过位移引伸计采集荷载和应变结果,进一步分析处理,得出相关因子的变化趋势。拉伸实验试件示意见图1。
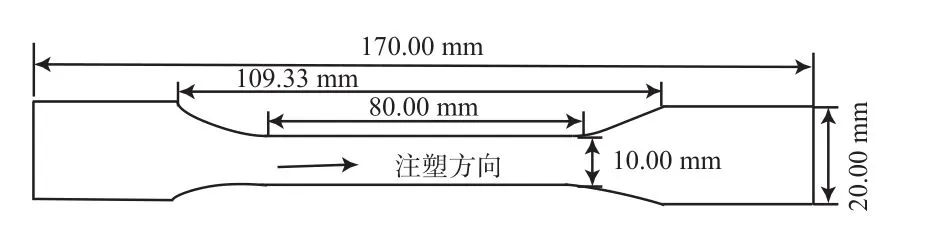
图1 拉伸实验试件示意Fig.1 Diagram of specimens for tensile test
1.4 性能测试
采用万能拉力试验机测试拉伸强度、拉伸应力及收缩率。收缩率按式(1)计算。

式中:ε为收缩率,%;L0表示初始温度(T0)时试样长度,mm;ΔT=T0-T1,T1为最终温度,T0取293 K;ΔL表示从T0到T1时的长度变化,mm;α表示平均线膨胀系数。
2 结果与讨论
2.1 测量系统验证实验
应变测量实验系统包括测量装置、分子泵机组、直流电源、应变测量模块、控温仪、计算机。实验中,通过分子泵机组维持测量装置内部真空状态,内部温度在二级G-M制冷机开启后逐渐降低,待降温稳定后(约为14 K)进行应变测量,利用直流电源加热,完成稳态温度点收缩率的测量,连续采集升温过程收缩率及温度作为实验结果。GFEP属于一种常见的工业材料,美国国家标准技术研究所收录了其收缩率的标准值,从图2可以看出:GFEP收缩率实验值与标准值具有较高的吻合度,说明应变测量实验系统测量较为准确。
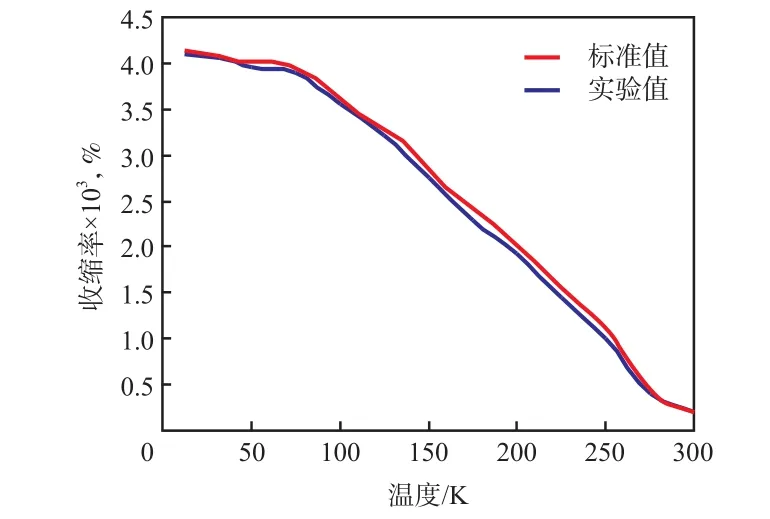
图2 GFEP收缩率随温度的变化曲线Fig.2 Shrinkage of GFEP as a function of temperature
2.2 GFEP的纵向和横向收缩率
在GFEP中,环氧树脂与玻璃纤维质量比为3∶7,纤维排布为单向铺陈。从图3看出:随着温度的上升,横纵向收缩率均变化不大;温度高于50 K时,随着温度上升,横纵向收缩率均快速下降。这是由于温度较低时,GFEP的内部链段和链节发生冻结,产生较小的原子振幅,因此,具备一定的硬脆性且不易发生变形。与纵向收缩率相比,GFEP横向收缩率更大,这是由于玻璃纤维的性能直接影响GFEP纵向热膨胀性,而树脂基体的性能则直接影响其横向热膨胀性。相同的温度区间中,GFEP横向收缩率是纵向收缩率的1.11倍。
从图4看出:温度为20 ℃时,GFEP具有较弱的非线性特征。原因是拉伸强度在0°时最高,随着角度从0°增加到90°,纤维增强作用减弱,造成拉伸强度减小;随着角度从0°增加到90°,拉伸方向纤维无明显增强作用,但由于泊松效应,沿着纤维方向会造成横向收缩,从而使纤维增强效果逐渐减弱。因此,拉伸强度逐渐减小。从图4还可以看出:在低温环境下,GFEP表现出较弱的线性特征,随角度的变化,力学性能变化规律基本一致。
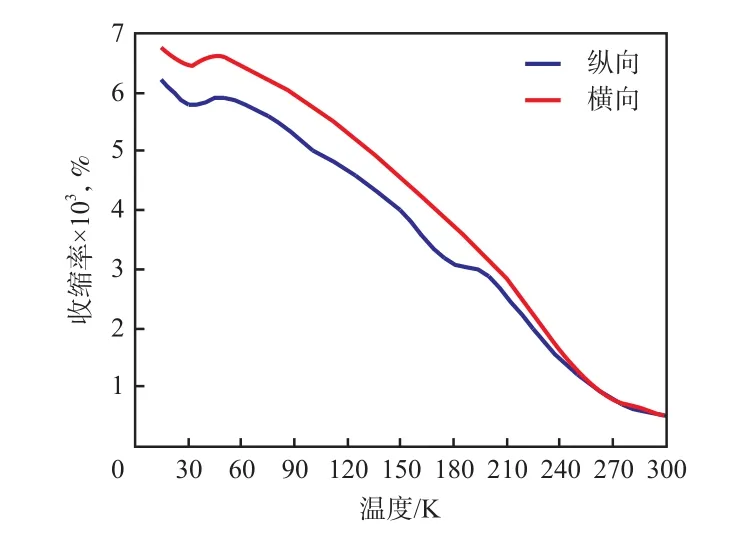
图3 GFEP纵向和横向收缩率随温度变化的曲线Fig.3 Longitudinal and transverse shrinkage of GFEP as a function of temperature
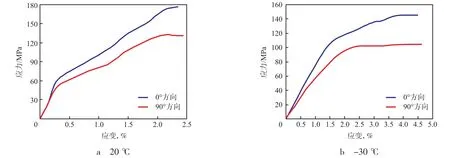
图4 20 ℃和-30 ℃时,GFEP的拉伸应力-应变曲线Fig.4 Tensile stress-strain curves of GFEP at 20 ℃ and -30 ℃
2.3 GFEP的低温和常温拉伸实验数据
从表1看出:低温和常温条件下,GFEP在0°时的弹性模量和拉伸强度均较90°时高,随温度升高,纤维对材料的增强作用减弱,拉伸强度和弹性模量随之减小。在低温条件下,GFEP的泊松效应较弱,随着温度升高,泊松效应增强,在温度较高时最明显。原因是随着温度的升高,GFEP的断裂应变增大,基体材料将变软;基体材料在温度降低时变脆,造成复合材料的整体断裂应变减小。
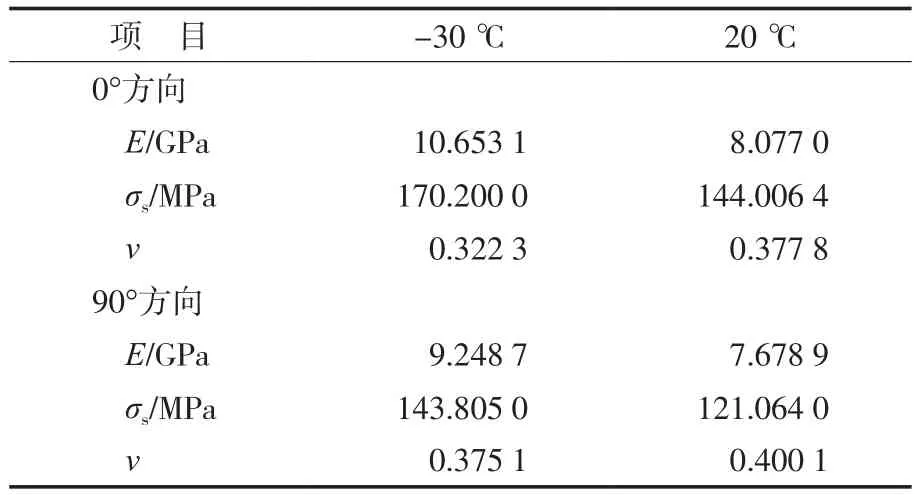
表1 GFEP的低温和常温拉伸实验数据Tab.1 Tensile test data of GFEP at low temperature and normal temperature
3 本构方程的建立
材料本构方程是对材料损伤和力学性能进行研究的基础,用来表征材料实际的拉伸应力-应变行为。假设复合材料拉伸应力-应变曲线的非线性行为[13]可用式(2)描述。

式中:ε为拉伸应变;ω为损伤因子。
假设复合材料的损伤因子可用式(3)描述[13]。
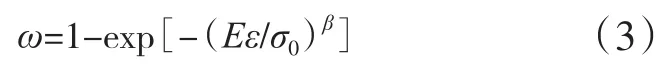
式中:σ0表示方程的尺度参数;β表示方程的形状参数。下同。
将式(3)代入式(2),得到式(4)所示的应力-应变关系,即本构方程。
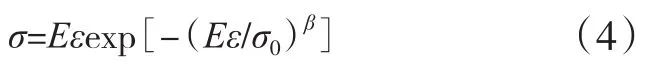
结合实验数据(见表1)可获得GFEP的本构方程参数,从表2可以看出:低温和常温条件下,GFEP的β差异较小;随着温度升高,σ0减小,原因是GFEP拉伸强度的极值用σ0表征,因此,σ0的大小和拉伸强度有关,随着温度的升高,拉伸强度减小,σ0也随之减小。

表2 GFEP本构方程参数Tab.2 Constitutive equation parameters of GFEP
材料剪切模型在承载过程中将会改变其弹性模量,采用90°方向拉伸实验测试,材料面内剪切弹性模量按式(5)计算。

式中:G12表示剪切弹性模量,GPa;εx表示GFEP在x轴上的应变分量,MPa;εy表示GFEP在y轴上的应变分量,MPa;σx表示GFEP在x轴上的尺度参数。
通过引入GFEP在90°方向试件的泊松比,式(5)可表示为式(6)。

通过二次函数拟合来处理GFEP在90°方向试件的拉伸应力-应变曲线,得到式(7)。
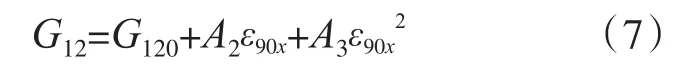
式中:A2,A3分别表示GFEP主方向面2、面3所受的压力,A2=56 175 MPa;A3=371 167 MPa;G120表示初始剪切模量,MPa。在受压时,为确保剪切弹性模量仍减小,当ε90x<0时,令A2=-56 175 MPa。通过材料参考坐标系和主应变的应变转换关系,ε90x可用式(8)表示。
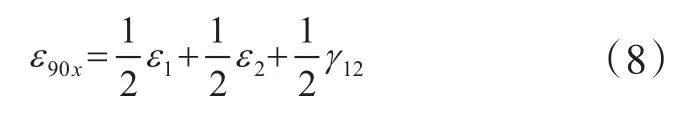
式中:ε1,ε2,γ12分别表示GFEP主方向面1、面2、面12三个面内的应变分量。因此,剪切弹性模量最终用式(9)表达。
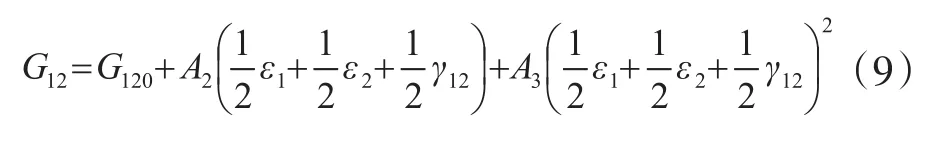
在0°和90°方向,通过建立GFEP的拉伸本构方程及弹性模量变化规律,可对GFEP在面内的应力-应变进行描述。
4 基于拉伸本构方程计算的有限元分析
本工作通过ABAQUS软件建立了实验试件模型(见图5),左端固定,施加位移的边界条件,右端施加4 mm位移。将GFEP本构方程编写到Umat程序中,可获得试件实验测试点应力-应变曲线和应力云图。
图5 实验试件模型Fig.5 Model of experimental sample
从图6可以看出:实验测试结果与ABAQUS模拟结果吻合较好。这表明通过Umat程序可预测0°方向和90°方向材料的应力-应变曲线的非线性行为。从图6还可以看出:90°方向拉伸时,两条曲线基本吻合,通过模拟获得的曲线和实验曲线无差异,整体具有基本相同的变化趋势,在拉伸应力上,两者几乎无差别,验证了材料本构方程的正确性。
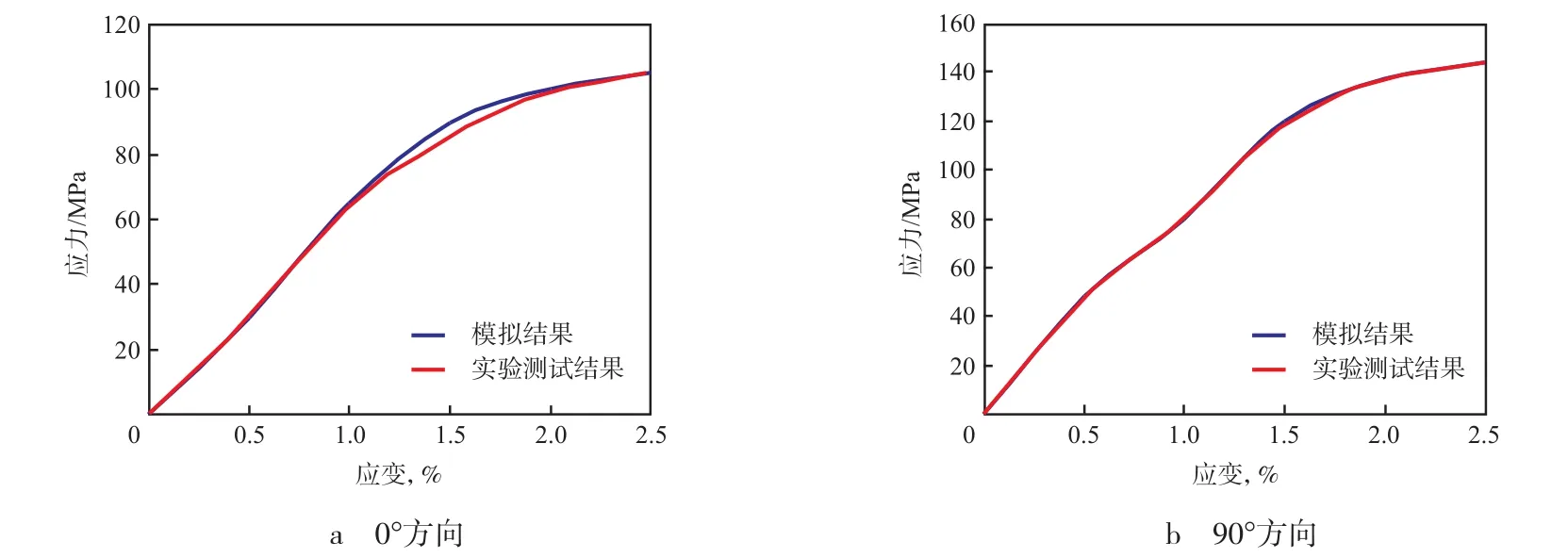
图6 测试点实验和有限元计算得到的0°方向和90°方向的应力-应变曲线Fig.6 Stress-strain curves of test point experiment and finite element calculation of 0° and 90°
5 结论
a)GFEP的力学响应在低温环境下的线性特征较弱,在常温环境下表现为较弱的非线性。
b)温度低于50 K时,随着温度升高,GFEP的横纵向收缩率均变化不大;温度高于50 K时,随着温度升高,GFEP的横纵向收缩率均快速下降。
c)-30 ℃时GFEP的拉伸强度和弹性模量较常温时大,非线性趋势随着温度降低越来越弱,断裂应变随着温度升高而增大。
d)通过Umat程序可预测0°方向和90°方向材料的拉伸应力-应变曲线的非线性行为。
e)测试点实验数据与有限元计算得到的90°方向上的应力-应变曲线比较吻合,在拉伸应力上,两者几乎无差别,验证了材料本构方程的正确性。
