基于对数误差的IOWGA算子的三角模糊数变权组合预测模型

谢小军，马 虹，邱云兰

（1.广州工商学院，广东 广州 510850；2.广东金融学院，广东 广州 510521）

0 引言

Bates和Grange在1969年首次公开发表了组合预测方法的理论[1]，预测实践表明组合模型能够提高预测精度，具有更好的泛化能力.因此组合预测模型逐渐成为预测领域研究的热点问题之一，并已经取得大量的研究成果.前期对组合预测方法的研究对象大多数是实数，但因事物预测模糊性和不确定性，很多时候是以区间数的形式表示，近几年对于区间数组合预测方法的研究较多[2-7].随着社会经济的不断发展，系统的复杂性和不确定性导致事物更具有模糊特征，三角模糊数成为了刻画事物的一种常见的不确定信息的表达形式，它弥补了实数和区间数的不足.因此构建基于三角模糊数的组合预测模型符合事物的实际发展趋势，研究三角模糊数组合预测模型既具有理论意义也具有现实意义.在已有的组合预测模型研究成果中，以三角模糊数作为研究对象的组合预测方法还不是很成熟，大多数是以对称三角模糊数进行建模预测.例如文献[8]将区间数转换为对称三角模糊数，以三角模糊数相似度作为最优准则度量指标，提出了一种基于三角模糊相似度的组合模型.文献[9]引入广义诱导有序加权平均算子，构建了基于对称三角模糊数及GIOWA算子的组合预测模型.文献[10]也是基于对称三角模糊数，将对称三角模糊数的利用面积中心和重心指标进行替代，运用IOWA算子建立了相应的三角模糊数面积序列和重心序列的相关系数的多目标组合预测模型，并引入重要性参数将其转化为单目标规划模型.因此，文献[11]基于三角模糊数面积型中心，面积型散度，质心三个指标的基础上，提出了一种以有效度为最优准则的三角模糊数组合预测模型.

本文旨在建立一种适用于普遍三角模糊数时间序列组合预测模型.首先从三角模糊数序列的整体性以及预测时各界点可能发生跳跃等考虑，基于文献[11]的研究基础，将三角模糊数序列三个界点序列转换成面积型中心、面积型散度、质心三个指标序列，转换后的序列同时受原三角模糊数的三个界点制约，然后引入诱导有序加权几何平均算子（IOWGA）算子，并以面积型中心、面积型散度、质心三个指标的对数误差为最优准则，通过引入偏好系数，建立了一种基于对数误差的IOWGA算子的三角模糊数变权组合预测模型，最后通过实例分析验证了该模型的有效性.

1 理论基础

定义 1.1[11-12]设三角模糊数 a＝（al，am，au），其中 al≤bm≤cu，满足 al－am＝au－am时，称为对称三角模糊数，满足al＝am＝au时，即为普通实数序列，令：

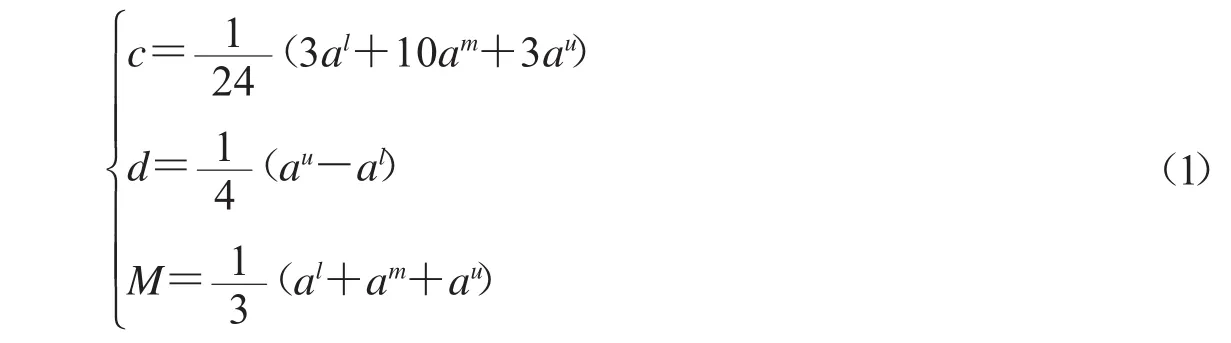
原三角模糊数a＝（al，am，au）转换成了面积型中心 c、面积型散度d、质心 M，记为（c；d；M），转换后的序列同时受到三角模糊数的三个界点的约束，即由（c；d；M）也可以推导出原三角模糊序列的三个界点，还原公式：

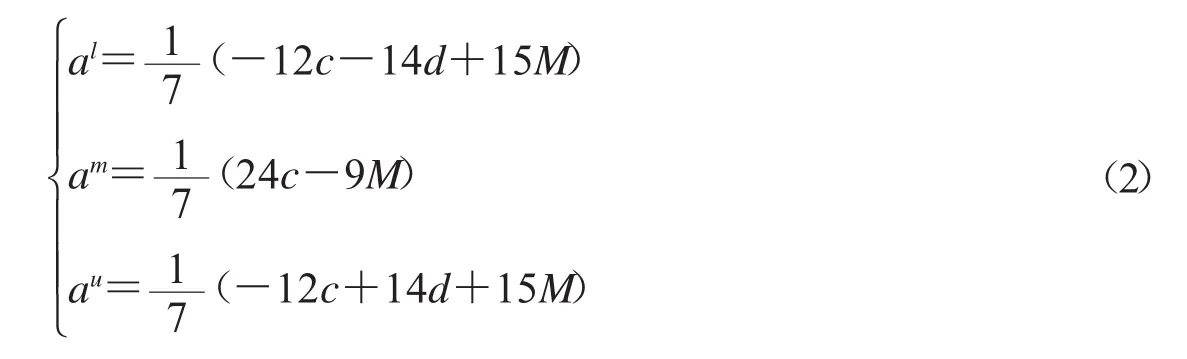
任意两个三角模糊数 a＝（al，am，au）和 b＝（bl，bm，bu），则有：

（1）a＝b⇔ al＝bl，am＝bm，au＝bu；

（2）a±b＝（al±bl，am±bm，au±bu）；

（3）ka＝（kal，kam，kau）.

定义 1.2[13]设 IOWGAW：Rn→R 为 n 元函数，W＝（w1，w2，…，wn）T为加权向量，满足若：

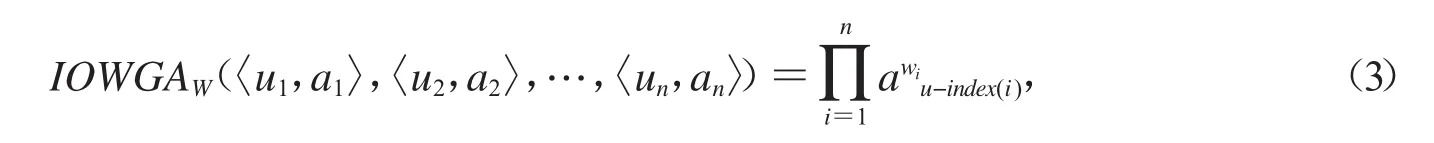
则称IOWGAW是u1，u2，…，un所构成的n维诱导有序加权几何平均算子，简记为IOWGA算子.

2 基于区间相似度的IOWGA算子的三角模糊数组合预测模型的建立

定义2.1设cit、dit、Mit分别为面积型中心、面积型散度、质心指标第i种方法的预测结果，令：

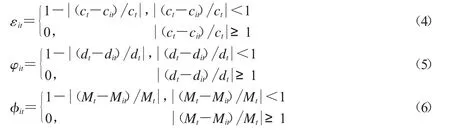
则称εit、φit、φit第i种方法在t时刻的面积型中心、面积型散度、质心指标预测精度.

利用定义3的εit、φit、φit作为定义2的诱导值，构建t时刻IOWGA算子产生的面积型中心、面积型散度、质心的预测值：

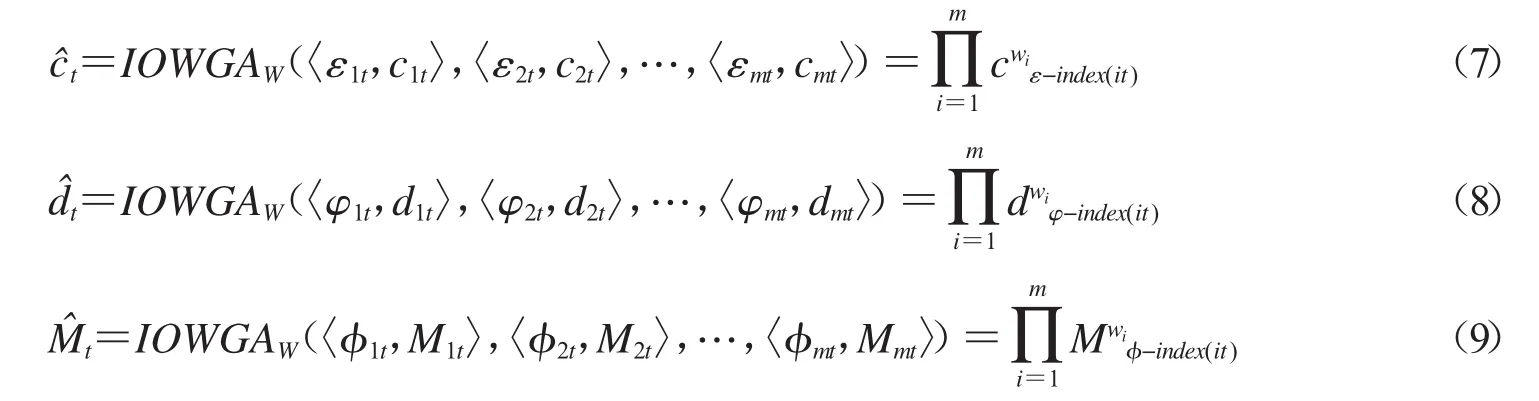
定义2.2令：

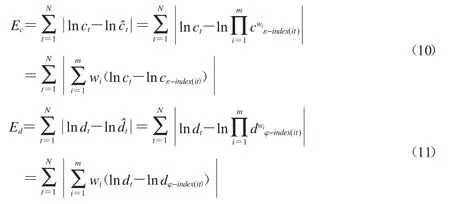
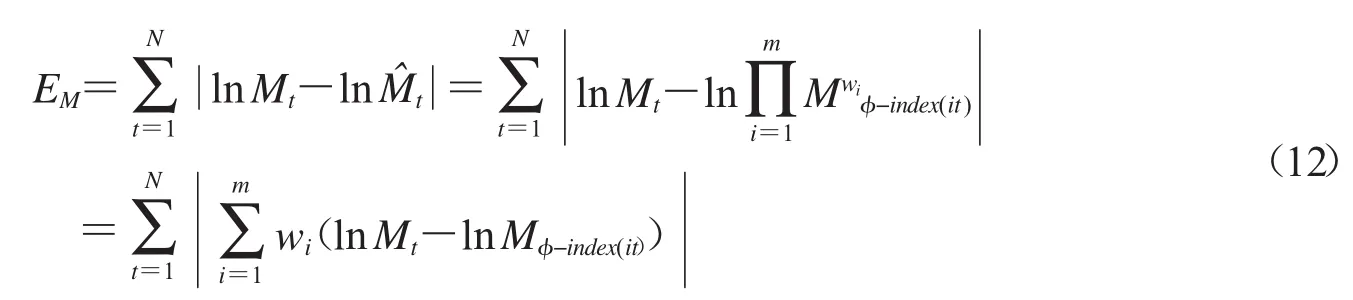
则称Ec、Ed、EM分别为基于面积型中心、面积型散度、质心指标的预测对数误差.显然Ec、Ed、EM越小，表示预测效果越好.

定义 2.3 引入偏好系数 α，β，γ，其中 α≥0，β≥0，γ≥0，且满足 α＋β＋γ＝1，令：

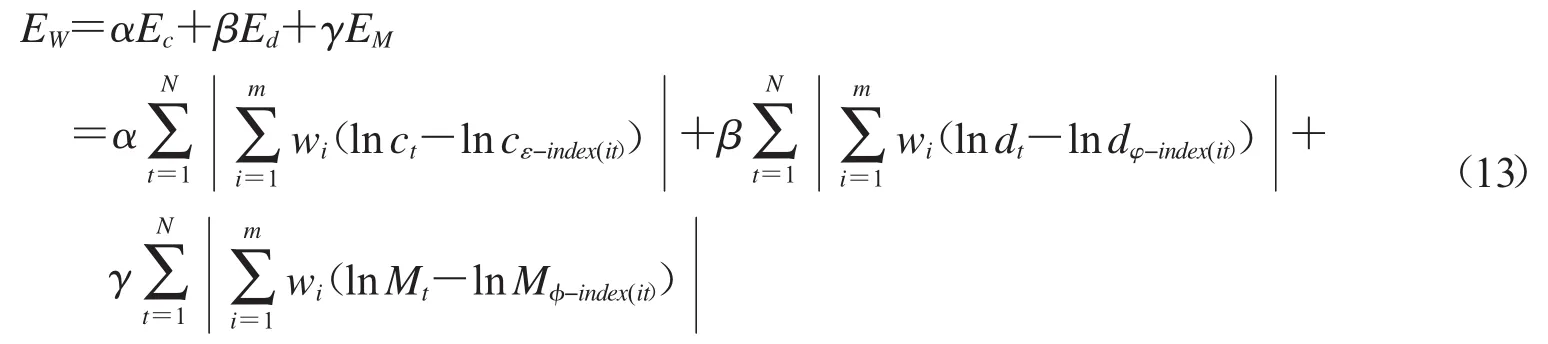
则称EW为对数误差，其中α，β，γ的取值由决策者确定，反映了面积型中心、面积型散度、质心指标对决策者的重要性考量.因此，可建立基于对数误差的IOWGA算子的三角模糊数组合预测模型为：

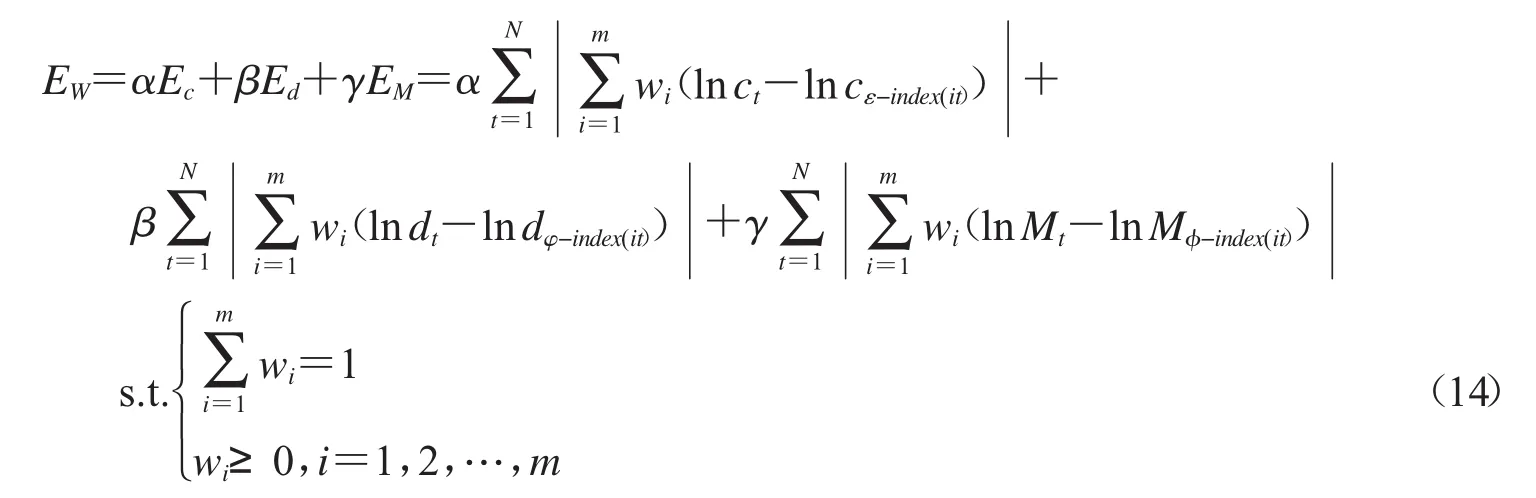
3 实例分析

为了验证基于对数误差的IOWGA算子的三角模糊数变权组合预测模型的有效性，以文献[2]的原始数据和单项预测方法的结果为研究基础进行实例分析，原始数据和各单项预测方法预测结果见表1.

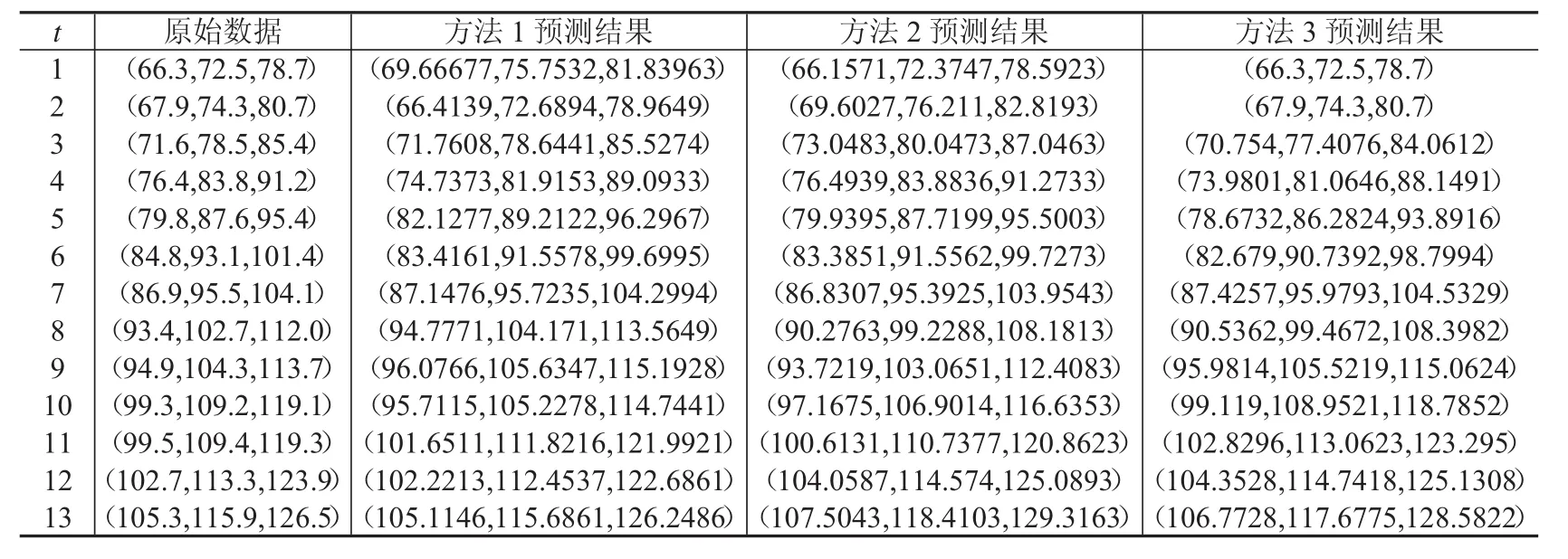
表1 实际三角模糊数序列与三种单项预测方法拟合预测结果

由表1数据代入式（1）可将三角模糊数序列转化为面积型中心、面积型散度、质心指标序列.利用式（4），（5），（6）可得到面积型中心、面积型散度、质心指标序列各单项预测方法的预测精度，见表2.将各指标各时刻精度值从大到小排列就能知道每个预测精度对应的预测三角模糊数（cε-index(it），dφ-index(it），Mφ-index(it）），利用式（7），（8），（9）计算，利用定义4，计算Ec、Ed、EM代入模型（14），确定偏好系数α，β，γ，文章选取了三组偏好系数值，分别是 α＝0.5，β＝0.3，γ＝0.2 和 α＝0.1，β＝0.2，γ＝0.7 以及 α＝0.2，β＝0.7，γ＝0.1，利用Lingo11计算求得对应的最优权系数，见表3.通过表3对应的最优权重系数，可以进一步计算得到组合模型下面积型中心、面积型散度、质心指标的预测值，然后利用式（2）还原为原始三角模糊数对应的预测值，结果见表4.

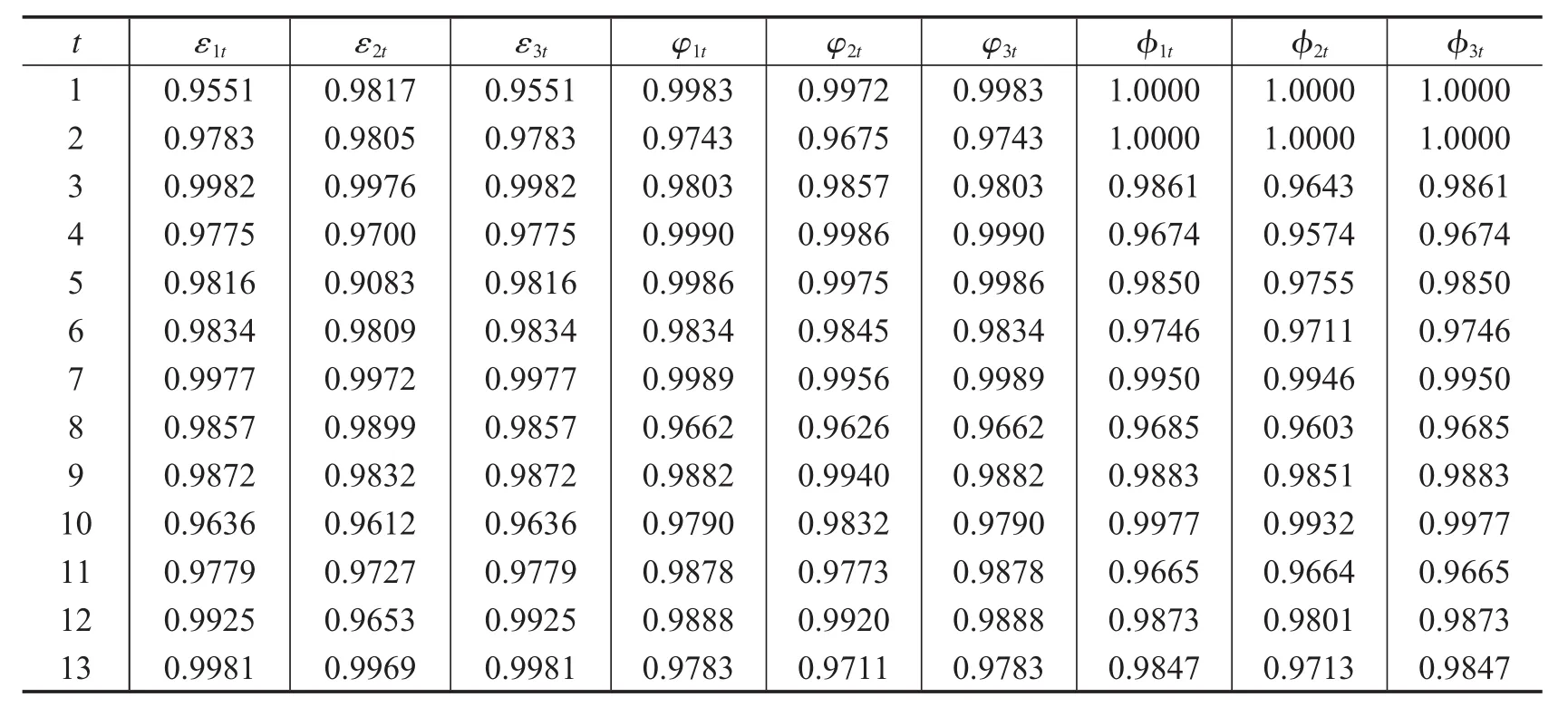
表2 单项预测方法各时点面积指标、中界点，重心指标序列的预测精度

表3 偏好系数不同取值对应下组合模型的最优权系数

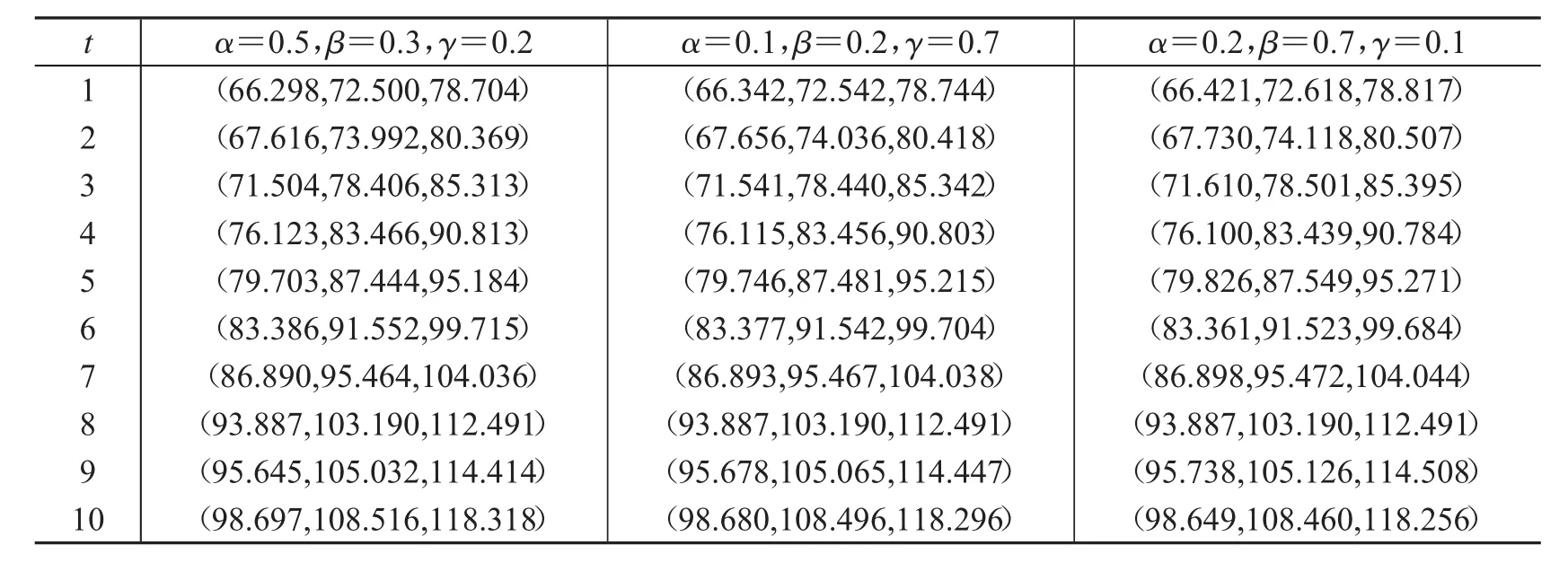
表4 偏好系数不同取值对应下本文组合模型三角模糊数预测值

本文除了与3种单项方法对比外，还选取了文献[11]的方法进行对比.利用基于三角模糊数下界点的预测均方误差（MSEL）、基于中界点的预测均方误差（MSEM）和基于上界点点预测均方误差（MSEU）、均方误差和（MSEI）来作为衡量其预测效果的指标，具体结果见表5.

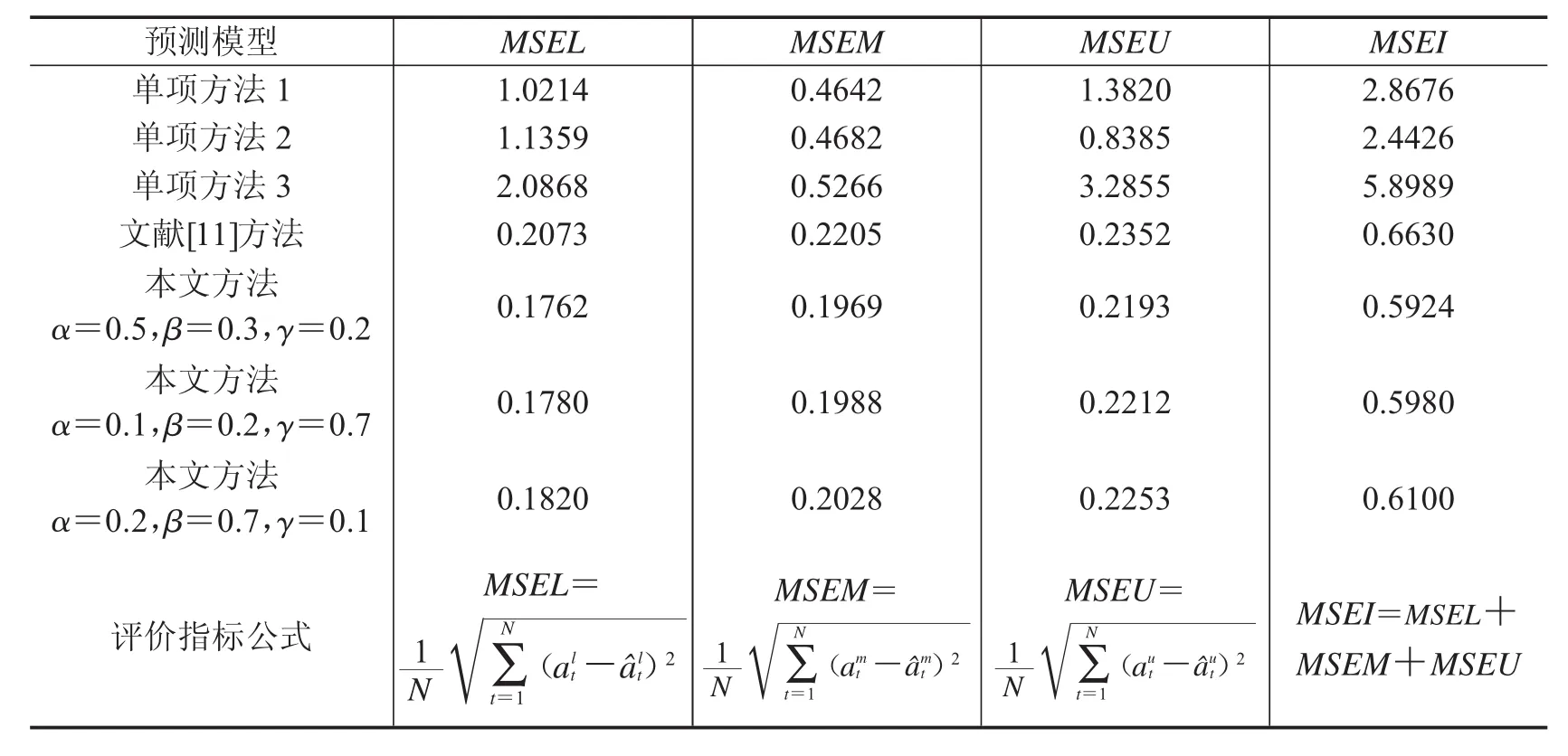
表5 本文组合模型与各单项预测方法预测效果评价指标

由表5可知：

（1）本文所提出的基于对数误差的IOWGA算子的三角模糊数变权组合预测模型的四个误差指标MSEL、MSEM、MSEU、MSEI都远小于所有单项预测方法的误差，因此本文提出的组合模型能够显著提高三角模糊数的预测精度；

（2）与文献[11]组合模型对比，本文提出的基于对数误差的IOWGA算子的三角模糊数变权组合预测模型四个误差指标MSEL、MSEM、MSEU、MSEI也都均小于文献[11]的方法的误差，且本文提出的组合模型可适用普遍三角模糊数序列的建模，可应用性更广，故本文提出的模型是有效的.

4 结语

针对三角模糊数序列的组合预测研究相对还不够成熟，通过对三角模糊数序列组合预测方法以及理论研究，建立了一种适用于普遍三角模糊数时间序列的三角模糊数变权组合预测模型.通过实例分析进一步验证了本文提出的模型的有效性，能够显著提高三角模糊数的预测精度，而且可适用性更加广泛，并且克服了组合模型定权的缺点.但是本文没有针对偏好系数的取值进一步分析所有的可能情况，故本文选取对应的模型可能不是最优的.因此，后期进一步工作讨论偏好系数取值不同可能对预测精度产生的影响.