新高考评价体系导向的高中数学创设问题情境

叶春林

日前教育部發布了《中国高考评价体系》，对评价模式提出新的要求，以达成高考不仅要对必备知识的考查，还要对核心价值、学科素养及关键能力的考查.而情境正是实现这种“价值引领、素养导向、能力为重、知识为基”的综合考查的载体.高考评价体系中所谓的“情境”即“问题情境”，指的是真实的问题背景，是以问题或任务为中心构成的活动场域.《普通高中数学课程标准（2017年版）》在教学建议中指出：“在教学活动中，应结合教学任务及蕴含的数学学科核心素养设计合适的情境和问题，引导学生用数学的眼光观察现象、发现问题，使用恰当的数学语言描述问题，用数学的思想、方法解决问题.”“根据数学学科的特点，高考数学试题情境可分为课程学习情境、探究创新情境、生活实践情境3类.”笔者以为，高中数学创设问题情境就是在数学教学过程中，教师根据教学需要，有针对性地提出真实、具体、生动的问题，以引起学生积极参与观察、描述、试验、归纳、抽象、概括等活动过程，激活学生思维，从而激发学生主动理解知识.把知识还原到情境中，让学生经历发现数学知识的全过程，增强学生理解力，培养创造力.“这样，学生主动获取知识的能力得到培养，学生的创新精神和创造力培养在数学课堂中得到了体现，所获得知识具有自我生成新知识的活力，学生对数学学习的兴趣也在无形中得到培养.”

本文以“直线与平面垂直的判定”第一节课的教学为例，谈谈笔者对新高考评价体系背景下的高中数学创设问题情境的实践和思考.

1数学课程学习情境

“数学课程学习情境包括数学概念习得、数学运算学习、数学推理学习等问题情境，关注已有知识的基础和准备程度.”本节课通过创设数学概念习得和数学推理学习问题情境开展直线与平面垂直的定义的教学.

问题1 空间中的一条直线和一个平面有哪些位置关系？

问题2 请举例说明，在我们生活中直线与平面相交的位置关系中最特殊的是什么？

问题3 你能回忆一下直线与直线垂直是怎样定义的吗？

意图 通过对已学知识的回忆，结合对日常生活事例的观察、感知、抽象，让学生直观感知直线与平面垂直的初步形象，激起学生学习的积极性.

问题4 请同学们思考下列问题（如图1）：

（1）在阳光下，你认为旗杆MN与它在地面上的影子ND所成的角是多少度？（2）当太阳移动时，影子ND也会随着移动，此时旗杆和它在地面上的影子所成的角度会改变吗？（3）旗杆MN与地面上不过点Ⅳ的任意一条直线EF是否垂直？为什么？

进一步提出，你能试着说出直线和平面垂直的定义吗？

设计意图 通过问题思考，让学生发现旗杆MN所在直线始终与地面上任意一条直线都垂直，与地面上的直线和旗杆所在直线是否相交无关.引导学生通过观察、分析进而让学生归纳出直线与平面垂直这一概念.

通过设计数学概念习得问题情境，引导学生开展观察、归纳、概括等数学思维活动，抽象出直线与平面垂直的概念.让学生经历概念的形成过程，注意关注学生已有经验，注重知识间的联系，把空间异面直线垂直的问题转化为平面直线相交垂直的问题进行研究.引导学生思考方向，渗透化归与转化数学思想方法.

问题5 （1）如果一条直线与平面内的无数条直线垂直，那么这条直线一定垂直这个平面吗？

（2）如果直线与平面垂直，那么这条直线一定会垂直于这个平面内的所有直线吗？

设计意图 设计数学推理学习问题情境，让学生对问题进行辨析讨论，深化直线与平面垂直的概念，理解线线垂直可以用定义来判定.

2数学探究创新情境

“数学探究创新情境包括推演数学命题、数学探究、数据分析、数学实验等问题情境，关注与未来学习的关联和数学学科内容的更深入的探究.”创设合适的数学探究创新情境可以更好地提高学生理性思维能力和数学探究能力，从而培养学生数学核心素养.

问题6 利用直线与平面垂直的定义直接判定直线与平面垂直需要具备什么条件？你认为要找这些条件方便吗？

设计意图 设计数学探究问题情境，通过学生思考、交流发现如果需要考察平面内的任意一条直线与已知直线是否垂直，这是很困难的.从中激发学生去寻找比定义判定更简捷、可行的判定方法.

问题7 这里能否用有限条直线来代替所有直线呢？一条可以吗？两条呢？

设计意图 让学生进一步探究问题，感受数学学习过程中可以尝试用有限来代替无限，但要通过数学实验或推理来验证这种尝试是否可行，从而逐步得到真理的过程，激起学生主动参与学习.

数学活动（折纸试验）：请同学们拿出课前准备好的三角形纸片，大家一起来做一个试验：过△ABC的一个顶点A翻折纸片，得到一条折痕AD，将翻折后的纸片竖放在桌面上（使BD，DC与桌面都接触）

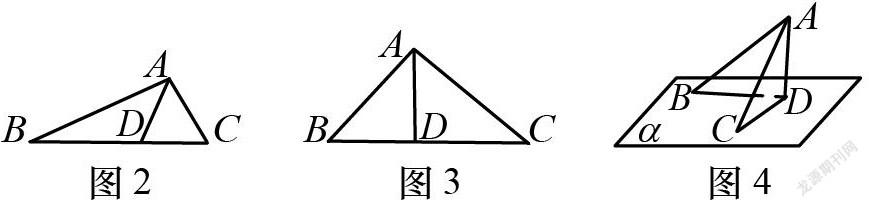
问题8 （如图2）（1）折痕AD与桌面一定垂直吗？（2）怎样翻折纸片才能确保折痕AD与桌面所在的平面一定垂直？（3）折纸试验结果反映的数学本质是什么？

（组织学生动手操作、探究、确认）

设计意图 设计数学实验探究问题情境，通过折纸让学生亲自动手、独立思考、自主探究等活动，发现当且仅当折痕AD刚好是BC边上的高时（如图3），且满足B，D，C三点不在同一直线上，此时AD才与桌面垂直（如图4）.让学生通过体验“直观感知、操作确认”的过程，让学生感知折纸结果反映的数学本质是线面垂直的判定方法.在试验过程中尽量让学生自己解释折纸方法的理由，让学生有辨析的机会，这样有利于培养推理能力.

问题9 在刚才的折纸片实验中，如果我们把折痕AD抽象成直线a，把BD，DC抽象成直线b，c，把桌面抽象成平面a，请同学们思考在什么条件下可以使直线a与平面a垂直？

设计意图 设计推演数学命题的问题情境，让学生通过操作确认，认识到两条相交直线一定要在平面内，从而体会到“平面内两条相交直线”是直线与平面垂直判定定理的关键条件.

问题10 如果改变图5中的两条相交直线m，n的位置，但仍使a⊥m，a⊥n（如图6），你认为直线a还能垂直于平面a吗？

设计意图设计数学推理学习问题情境，让学生知道判定一条直线和一个平面垂直，只要这个平面内有两条相交直线与已知直线垂直即可，与它们是否有公共点没有关系.

问题11

（1）判定一条直线与一个平面是否垂直既可用定义也可用判定定理，你觉得用判定定理的优越性体现在哪里？（2）你觉得定义与判定定理共同点是什么？

设计意图 设计数学探究问题情境，引导学生对比定义和判定定理，让学生体会到在研究数学问题时往往可以把无限问题转化为有限问题，通过发现定义与判定定理的共同点，感悟到可以把空间问题转化为平面问题、把线面垂直问题转化为线线垂直问题的数学思想.

问题12 如图7，已知a∥b，a⊥a，求证：b⊥a.

设计意图 设计推演数学命题的问题情境，通过学生思考、交流等活动过程，引导学生用判定定理或定义证明新命题，进而巩固知识的运用.让学生了解这个命题也可以判定直线和平面垂直，命题体现了空间中平行与垂直之间的联系.

3生活实践问题情境

“生活实践情境是需要学生将问题情境与学科知识、方法建立联系，应用学科工具解决问题;生活实践情境关注与其他学科和社会实践的关联，是考查学生数学应用素养、理性思维素养和数学文化素养的重要载体.”生活实践情境在培养学生学科素养和关键能力上起着重要作用，但在我们以往教学中重视不够.新高考理念倒逼数学教师以生活情境強化学生数学学科核心素养的指导发展.

问题13 探究：如图8，在直四棱柱A'B'C'D'-ABCD（侧棱与底面垂直的棱柱称为直棱柱）中，底面四边形ABCD满足什么条件时，A'C⊥B'D'？

设计意图 设计生活实践问题情境，学生已经学习了线面垂直的判定定理，让学生通过探究、实践定理的作用，进而让学生体会转化思想在生活实践问题中的作用.

问题14 学校要安装一根12米高的旗杆，要保证旗杆所在的直线垂直于地面所在的平面，请设计安装方法，并说明设计理由.

设计意图 设计生活实践问题情境，体现用所学知识解释实际生活中的问题，增强学生应用数学意识.

4 结束语

新发布的《普通高中数学课程标准（2017年版）》和《中国高考评价体系》，对高中数学教学提出新的要求，对课堂教学的引导更具体、更合理.在新的背景下高中课堂教学中创设问题情境会被更广泛应用，它对数学教学活动必将产生促进作用.在高中数学课堂中设置恰当的问题情境可以刺激学生的学习，转变被动学习的行为，使学生主动地接受数学知识，让数学观念得到自主建立;可以更好地培养学生科学态度和责任，落实育人目标;可以让学生经历分析问题、解决问题的过程，积累学习经验，提升分析问题、解决问题的能力.

我们知道，问题是数学的心脏，通过学生与情境、问题的有效互动，可以让数学学科核心素养更好地得到形成提升巩固.数学知识转化为数学学科核心素养的重要途径就是问题情境.因此，创设丰富的课程学习、探究创新、生活实践等问题情境，让学生从中探求知识的认知路径，是数学知识通向数学学科核心素养的必然要求.