一类3阶非线性时滞微分方程振动解的存在性
2021-02-28赵玉萍
重庆理工大学学报(自然科学) 2021年1期
赵玉萍,傅 华
(1.青海民族大学 数学与统计学院,西宁 810007;2.福建警察学院,福州 350007)
微分方程在生物药学、经济学、计算数学、物理学等领域应用非常广泛。微分方程的研究越来越受到人们的关注。近年来,关于微分方程振动性的研究成果很丰富[1-5],对于1阶、2阶微分方程振动解的存在性研究也不少[6-9],但对于3阶非线性时滞微分方程振动解的存在性、渐进性研究较少[10]。BACULIK OVAA B等[1]只研究了3阶非线性微分方程解振动的充分条件,并没有考虑解的存在性问题。
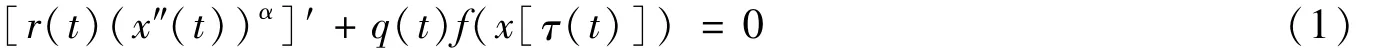
利用分析法和Schauder Tychonoff不动点定理研究一类3阶非线性时滞微分方程
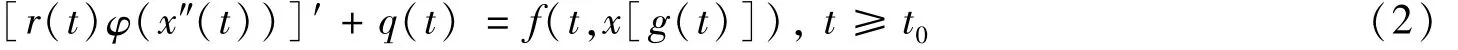
振动解的存在性。同时,研究了式(2)的特殊形式
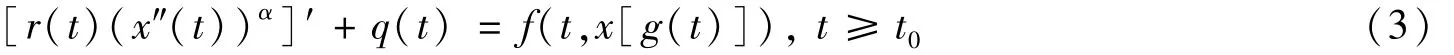
振动解的存在性。这里r(t)∈C1([t0,+∞),R+),q(t),g(t)∈C([t0,+∞),R),f(t)∈C([t0,+∞),是奇正整数之商,α≥1。
1 主要结果
定理 设存在常数η>0,当r(t)>η时,
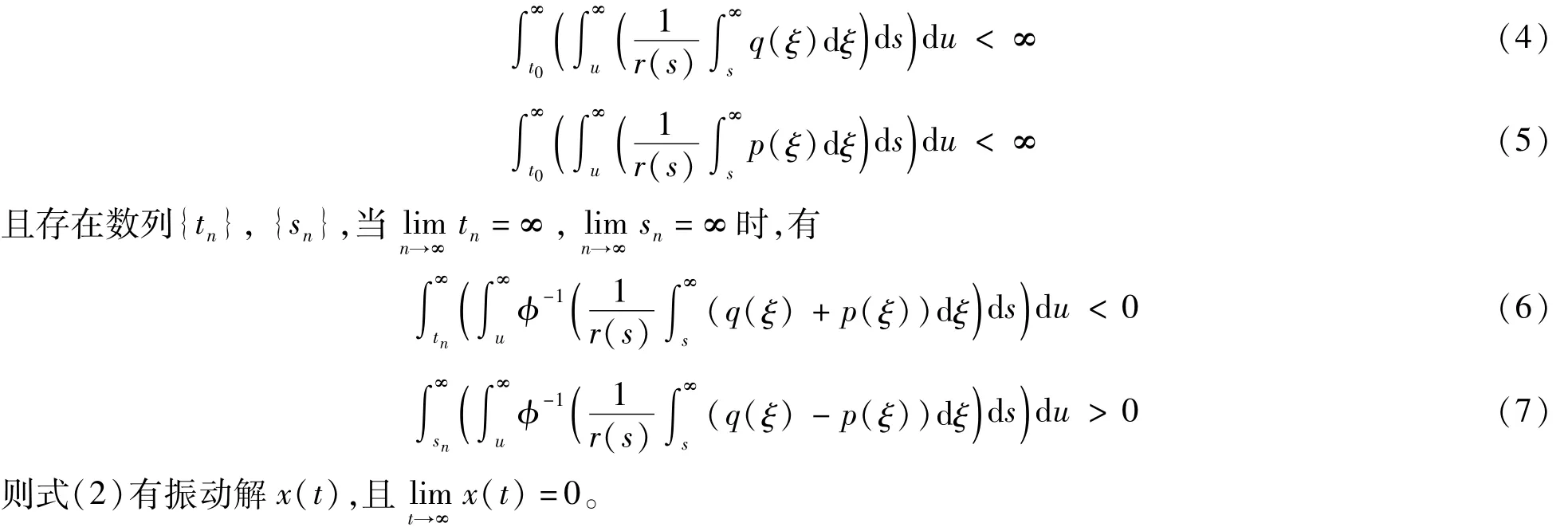
证明 利用Schauder Tychonoff不动点定理进行证明。由式(4)和(5),对任意r>0,-Tr>t0,当t>Tr时
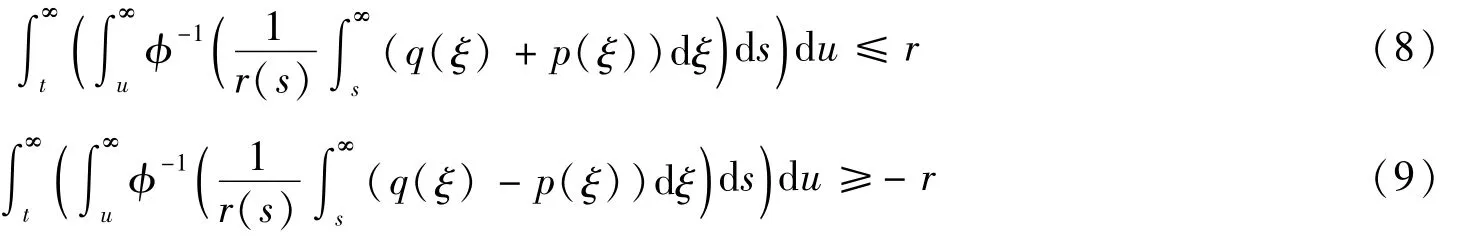
设C[T0,∞]是区间[T0,∞]的紧子空间上具有拓扑一致收敛的所有连续函数组成的局部凸空间。这里,T0=inft≥t0g(t)。
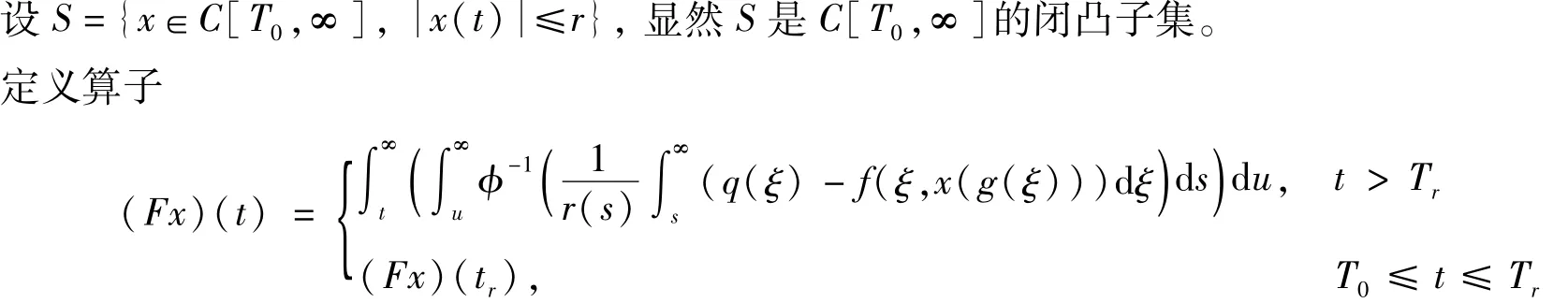
显然对 x∈S,(Fx)(t)在[T0,∞]连续。由式(8)和(9)
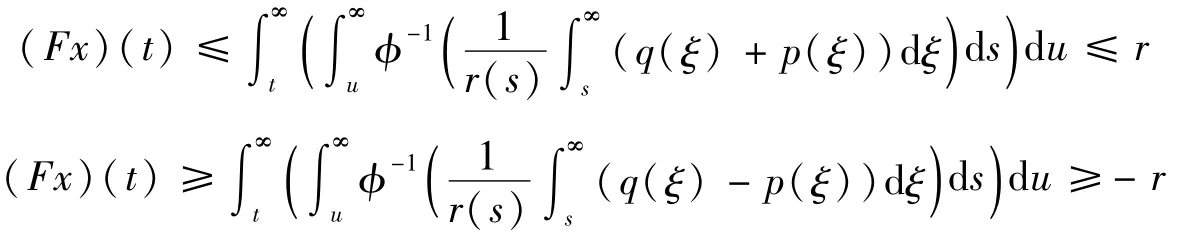

所以F在S上连续。当t2,t1≥T0时,
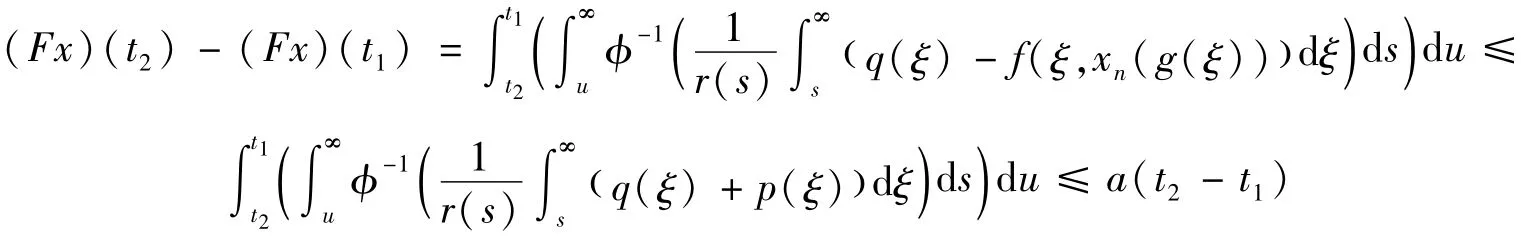
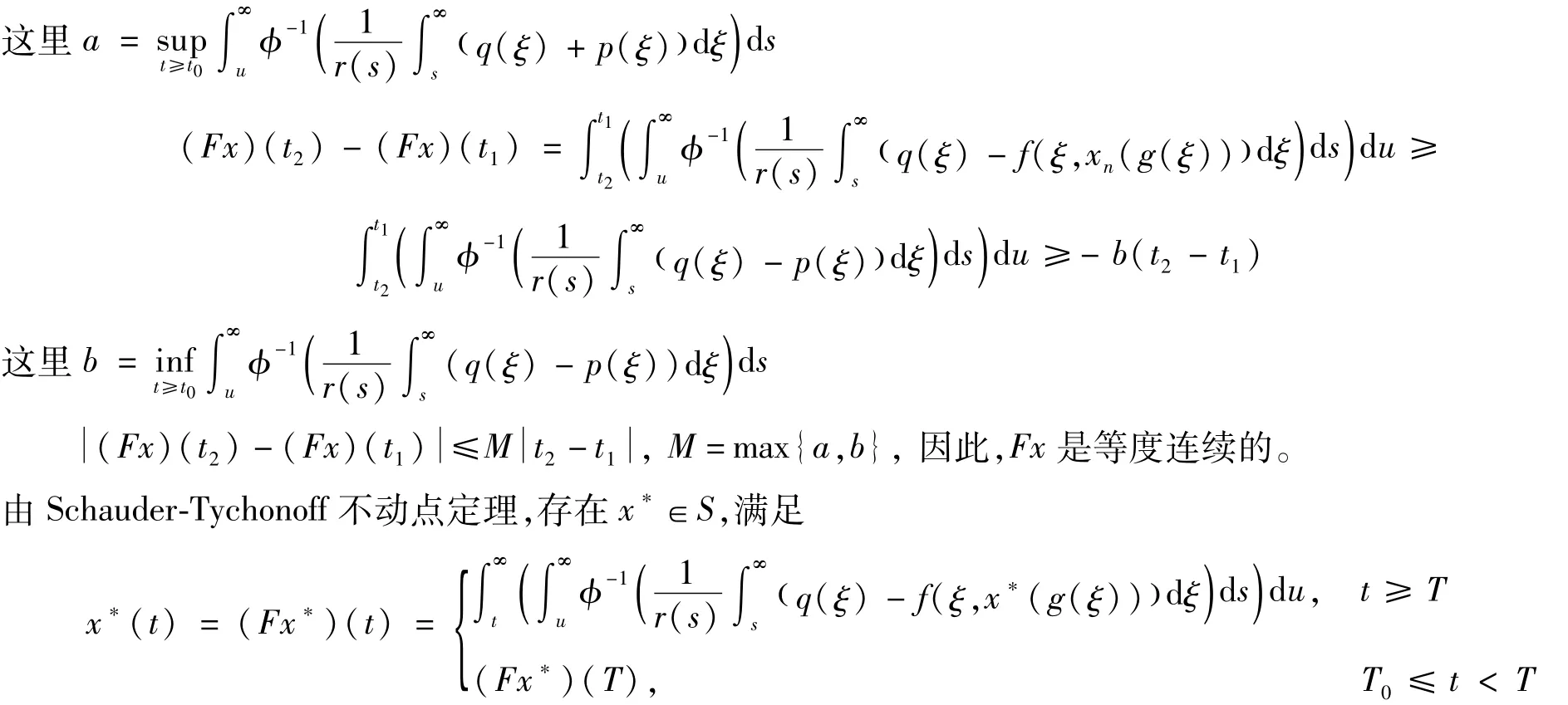
另外,由式(6)和(7)
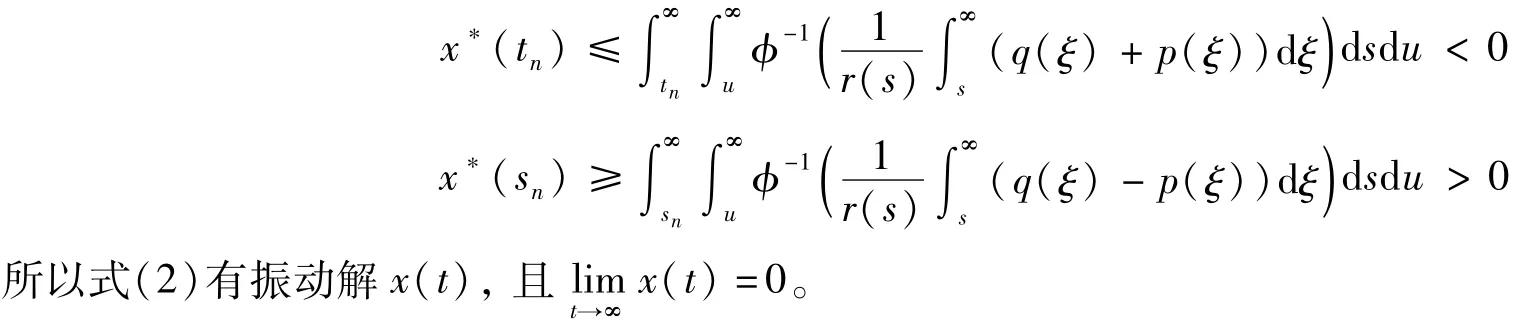
下面讨论式(3)解的存在性:

证明 (u)=uα,由式(4)和式(5),对任意r>0,-Tr>t0,当t>Tr时
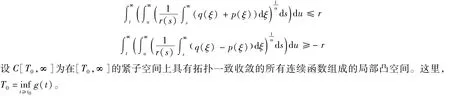
定义算子
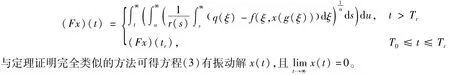
例1 考虑3阶微分
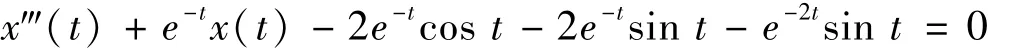
这里,

例2 考虑3阶微分