具有导数项的分数阶微分方程解的存在唯一性

温世林，韩 伟，桑彦斌

（中北大学 理学院，太原 030051）

1 相关进展

分数阶微分方程已经广泛应用于物理、化学、生物、工程等各个领域［1－3］，对分数阶微分方程的研究具有重要的理论和应用价值。特别是具有多种边界条件的分数阶微分方程，近年来引起人们的极大兴趣，对其研究主要集中在非线性分数微分方程边值问题正解的存在性、多重性和唯一性。LI等［4］研究了如下非线性分数阶微分方程边值问题正解的存在性，其中Dα0＋，Dv0＋为标准的Riemann Liouville分数阶导数：

Wang等［5］利用格林函数的性质和锥理论，讨论了如下高阶非线性奇异分数阶微分方程的唯一存在准则：

Jleli等［6］利用混合单调算子方法对以下任意阶非线性分数阶微分方程正解的存在唯一性进行了研究，其中n＞3（n∈N），f、g为连续函数。

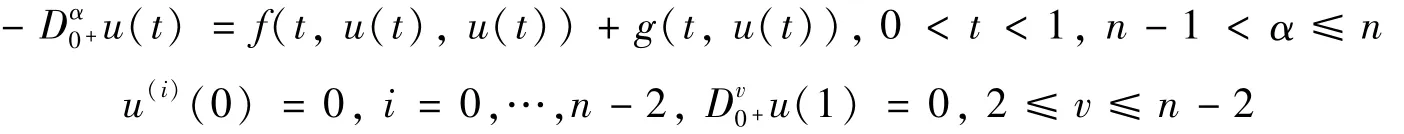
本文中将研究如下具有导数项的分数阶微分方程正解的存在唯一性：

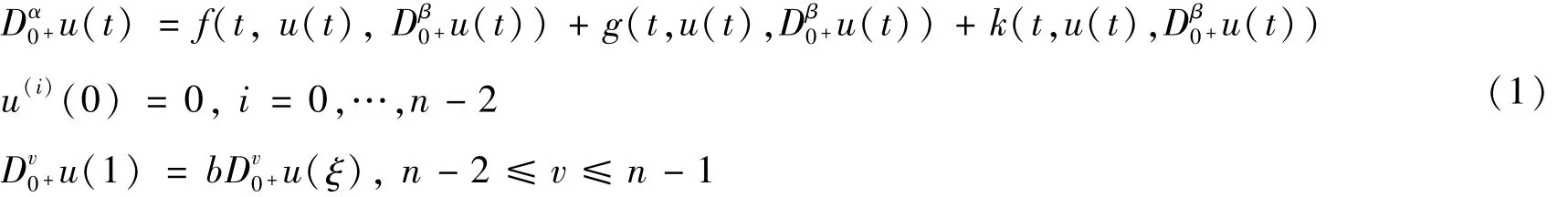
其中：Dα0＋，Dβ0＋，Dv0＋为标准的Riemann Liouville分数阶导数，0＜t＜1，n－1＜α≤n（n∈N，n≥2），n－2＜β≤v≤n－1，0≤b≤1，ξ∈（0，1），α－v－1≥0，0≤bξα－v－1＜1。应用文献［7］中算子方程，其中A，B，C∶P×P→P是混合单调算子：

2 预备知识和相关引理

本节简单介绍了一些定义、符号和已知结果［8－10］。

定义1 A∶P×P→P是1个混合单调算子，如果A（x，y）在x上递增，在y上递减，则x（x∈P）为A的不动点［11］。

定义2 A∶D（A） E→E，若对 x，y∈D（A），x≤y，t∈（0，1），有A（tx＋（1－t）y）≤tAx＋（1－t）Ay，称A为凸算子。若A为凸算子，则－A为凹算子［12］。

集合E＝｛x｜x∈C［0，1］，D0β＋x∈C［0，1］｝为实Banach空间，定义它的范数为： x（t） ＝max｛t∈m［a0，x1］｜x（t）｜，t∈m［a0，x1］D0β＋｜x（t）｜｝。E被赋予一个半序关系：若u（t）≤v（t），D0β＋u（t）≤D0β＋v（t），那么u v。设P E，定义：P＝｛x∈E∶x（t）≥0，D0β＋x（t）≥0， t∈［0，1］｝，显然P是1个正规锥且Ph∈E。

引理1 P是E中的1个正规锥，假设A，B，C∶P×P→P是3个混合单调算子，并且满足如下条件：

3）对y∈P中任一点，C（·，y）∶P→P为凹算子；对x∈P中任一点，C（x，·）∶P→P为凸算子；

4）-h∈P，h＞θ使A（h，h）∈Ph，B（h，h）∈Ph，C（h，h）∈Ph；

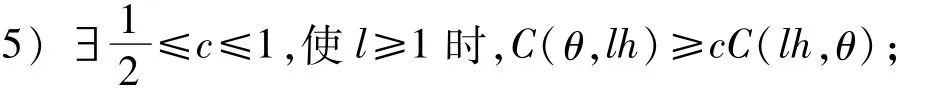
6）存在常数 δ0＞0，对于 x，y∈Ph，B（x，y）＋C（x，y）≤δ0A（x，y）；

那么算子方程（2）在P中有唯一正解x ，满足μh≤x ≤λh，λ、μ为2个正实数。对任意的初始值x0，y0∈Ph，依次构造如下序列：在E中，n→∞时，xn→x ，yn→x 。

3 主要结果

许多问题都可转化为算子方程（2）［13－18］。本节将研究方程（1）正解的存在唯一性。

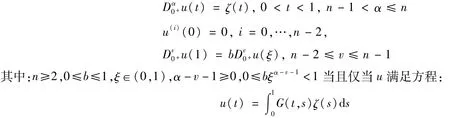
其中

引理2 G（t，s）满足如下性质：

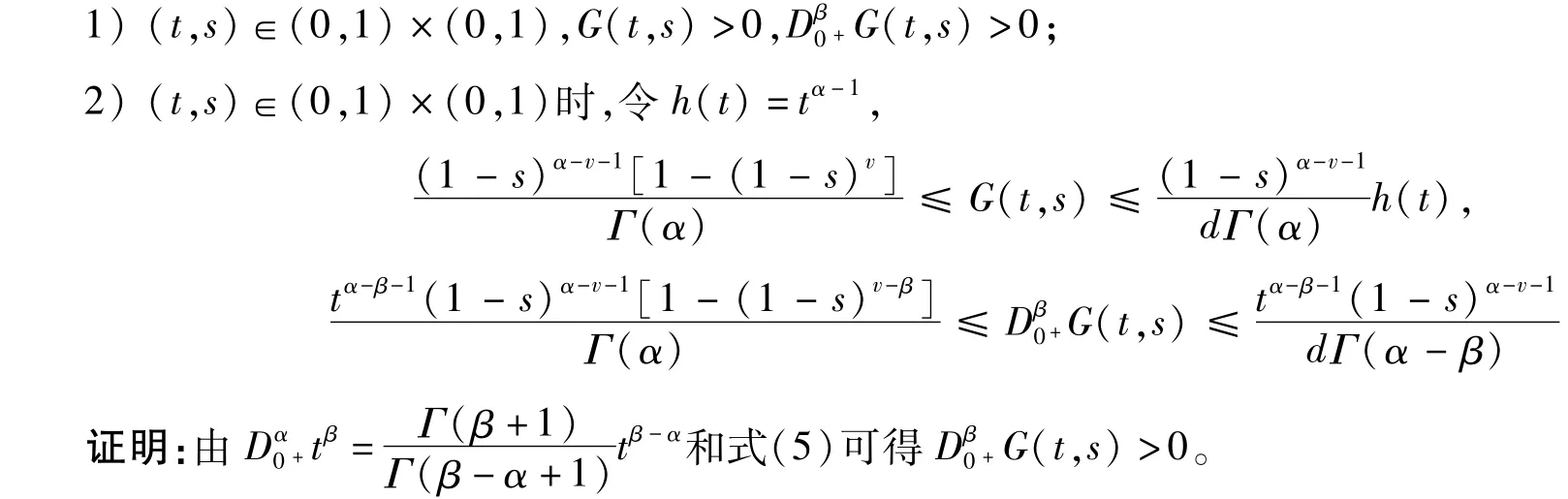
式（2）后半部分不等式的右边由0≤b≤1和0＜d＝1－bξα－v－1≤1易得。下面证明左边：

当0≤s≤min｛t，ξ｝＜1时，

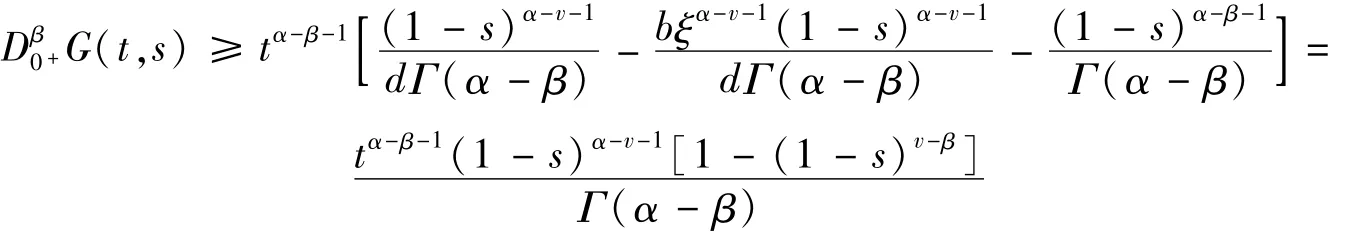
当0＜ξ≤s≤t≤1时，由0＜d＝1－bξα－v－1≤1，

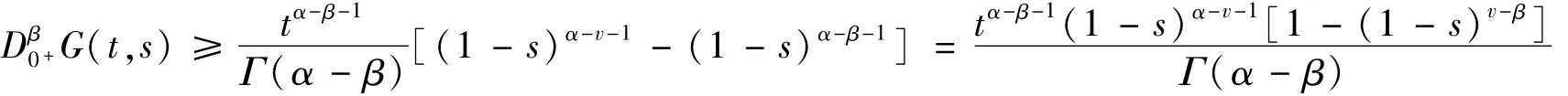
当0＜t≤s≤ξ≤1时，

当0≤max｛t，ξ｝≤s≤1时，

定理1 假设如下条件成立：

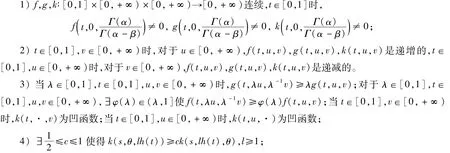
5）存在常数 δ0＞0，对 t∈［0，1］，u，v∈［0，＋∞），g（t，u，v）＋k（t，u，v）≤δ0f（t，u，v）；那么方程（1）在P中存在唯一正解u ，满足 μtα－1≤u ≤λtα－1，t∈［0，1］，λ、μ为2个正实数。

证明：从文献［5］可知方程（1）解的积分公式如下，其中G（t，s）在式（5）已给出。

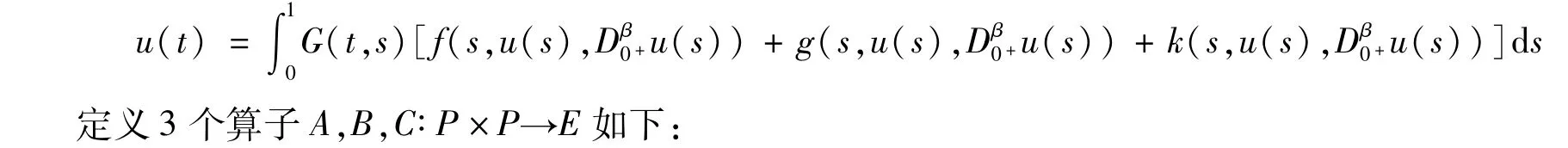
其中X＝A，B，C，p＝f，g，k。

容易证明当且仅当u＝A（u，u）＋B（u，u）＋C（u，u）时，u是方程（1）的解。

从假设条件1）和引理2可以得出，A（u，v）≥0，Dβ0＋A（u，v）≥0，即A∶P×P→E。同理可得B，C∶P×P→E。下面证明A，B，C是混合单调算子：

对于固定的t∈［0，1］和v∈［0，＋∞）， a∈（0，1），u1，u2∈P，

同理可得：

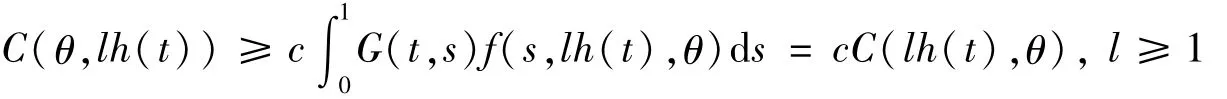
同理可得Dβ0＋C（θ，lh（t））≥cDβ0＋C（lh（t），θ），即满足引理1的条件5）。从定理1的条件5）可知，u，v∈P

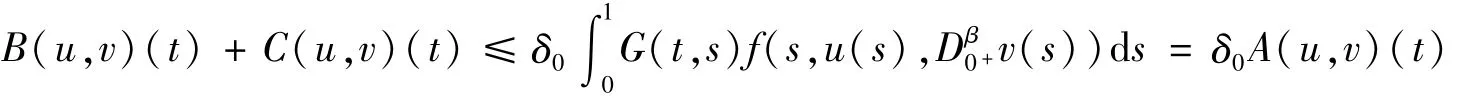
同理，D0β＋（B（u，v）（t）＋C（u，v）（t））≤δ0D0β＋A（u，v）（t），所以算子A满足引理1的条件6）。因此定理1的条件满足引理1。证毕。