期望损失（ES）的几种逼近法比较

魏正元，李 乔，王 雪，郑小洋

（重庆理工大学 理学院，重庆 400054）

在险值（value at risk，VaR）和期望损失（expected shortfall，ES）是2种常用且重要的风险度量值，且2个量都是不可直接观测的，VaR直观、简单，ES属一致性风险度量，故而关于这2个量的研究一直备受学者和市场从业者的关注，相关的著作和文献较多［1－3］。然而ES的积分运算不一定有闭式表达式，因而很有必要研究其近似计算和数值解法。

在未知总体分布情况下，SIMONATO JG［4］应用Johnson分布的前四阶矩计算VaR和ES，GRAZIA Z M等［5］使用Gram Charlier展开对数据进行建模，得出风险度量的封闭形式，Amédée Manesme CO等［6］探讨了校正的Cornish Fisher在风险度量中的应用，Arevalillo JM［7］研究了Saddlepoint反演。本研究将Edgeworth和Saddlepoint引入ES的计算，并与bootstrap的结果进行比较，结果表明Edgeworth和Saddle point在VaR的计算中相差无几，但在计算ES时，Edgeworth展开比Saddlepoint展开简单且具有更高的精确度。

设某个金融头寸在持有期L内的损失变量X的概率分布函数为FX（x）（本文用资产收益率γt刻画风险，空头用X＝γt，多头用X＝－γt），且E［｜X｜］＜∞，给定尾部概率p（0＜p＜1），ES的定义为［6］

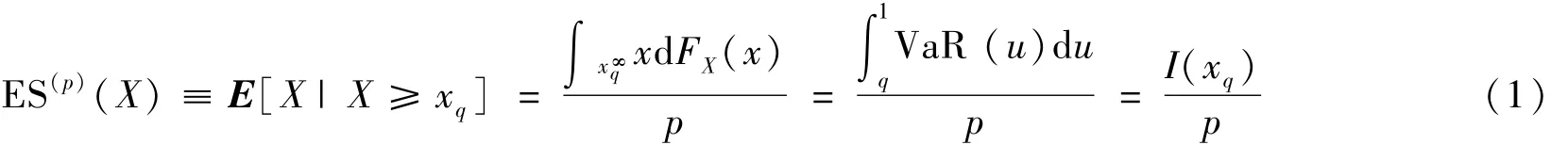
这里xq＝F－1X （p）是X的q＝1－p右侧分位数，从风险度量角度是VaR值xq＝VaRp（X）。ES为损失超过VaR值的期望，也就是条件在险值（CVaR）。

1 主要结果

定理1 若损失随机变量X满足Cramer’s①如果sup t→∞ ｜E F（eitX）｜＜1，则X满足Cramer’s条件条件，则式（1）中I（xq）的估计值为

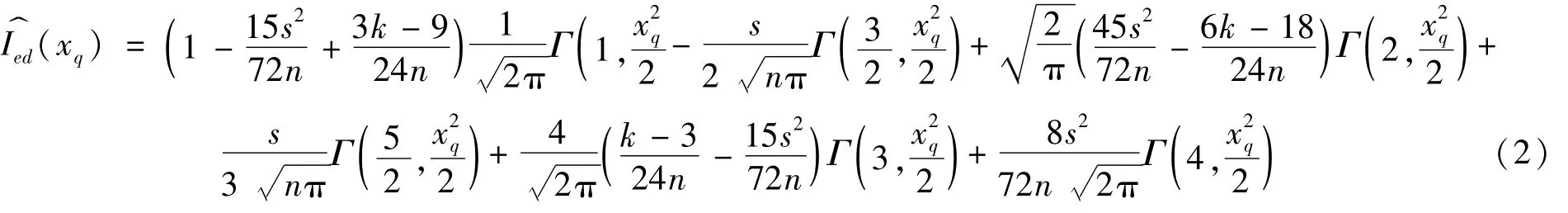
证明 如果连续型随机变量X前4阶矩存在，其q分位数的Cornish Fisher展开和概率密度函数的Edgeworth展开有如下形式［8］

式中

出I（xq）的值，通过Edgeworth展开得到一个不完全gamma函数的解析表达式，使尾部积分的计算得以实现。

定理2 设X1，X2，…，Xn是来自总体F（x）的iid样本，则式（1）中I（xq）的估计值为

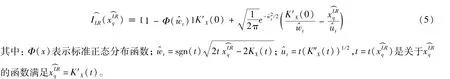
证明 若iid样本X1，X2，…，Xn～f（x），记MX（t）＝E［etX］和KX（t）＝log MX（t）为X的矩母函数和累积量生成函数，Tn＝（X1，X2，…，Xn，F）为某标准化的渐近正态统计泛函，记Fn是Tn的分布函数，Mn（t）为Tn的矩母函数，

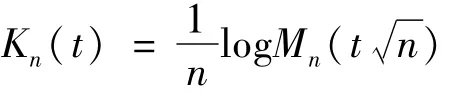
为Tn的累积量生成函数（Cumulant generating function）。令

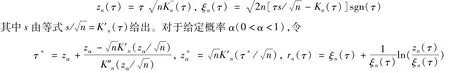
由文献［7］中的结论可得Saddlepoint展开计算的分位数为

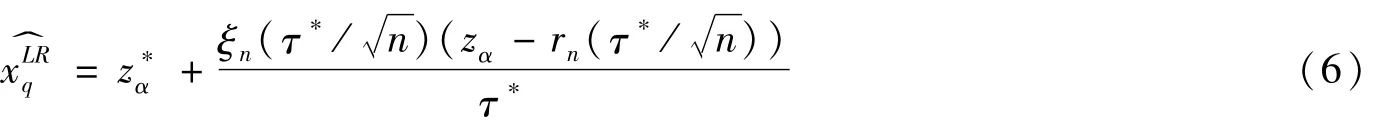
第二步近似I（xq），将Saddlepoint展开计算的分位数与Broda［9］给出的近似方法相结合可得

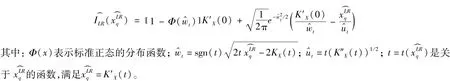
2 模拟计算

Bootstrap属非参数统计方法，它将观测样本看作有限总体，通过对观测样本进行重复抽样得到Boot strap样本，进而对总体分布的未知参数进行推断。若x1，…，xn为损失随机样本观测值，x（1），…，x（n）为其次序统计量，令l＝nq，qi＝li／n，l1和l2表示nq的最近邻的2个正整数，那么分位数xq的估计为

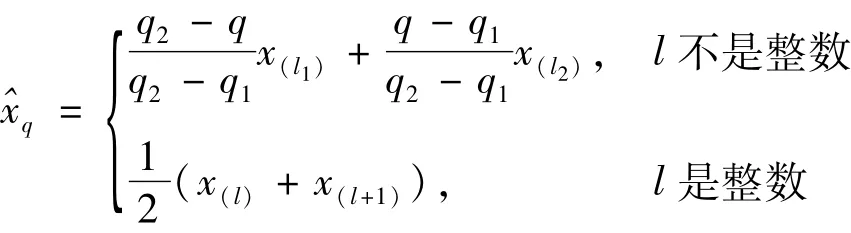
从观测样本x1，…，xn抽取Bootstrap样本，重复抽样次数为B，那么基于Bootstrap计算的VaR为

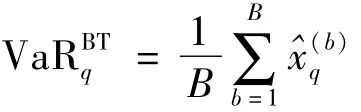
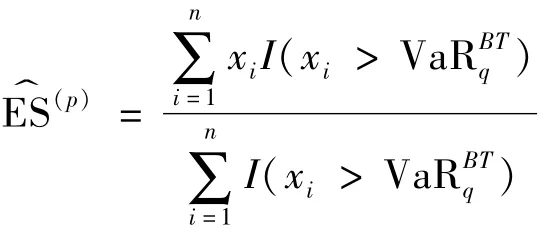
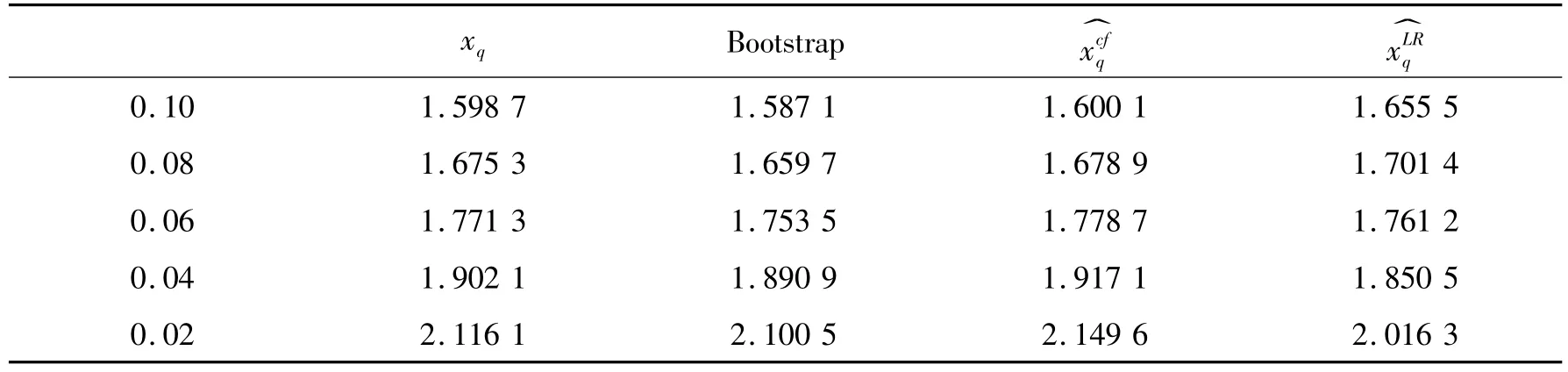
表1 分位数理论值和3种方法在不同尾部概率下的估计值

从表1中分位数估计可以看出：Bootstrap和Cornish Fisher估计更接近真实值，Saddlepoint估计虽然在精确度上次之，但相对误差未超过5%。从图1可以看出I（xq）的计算结果，Edgeworth展开拟合值和Bootstrap拟合值与真实值更为接近，一定程度上说明Edgeworth展开在计算ES值时比Saddlepoint展开更为精确。

3 实证分析

本文中采集阿里巴巴2019年6月1日到8月1日的股票收盘价格Pt共41个，从多头的角度，以日对数收益率Rt＝log（Pt）－log（Pt－1）来进行实证分析。运用Saddlepoint展开时，以双指数分布拟合收益率数据。收益率数据通过核密度估计、Saddlepoint展开和Edgeworth展开拟合的4个密度函数分别如图1、2所示。

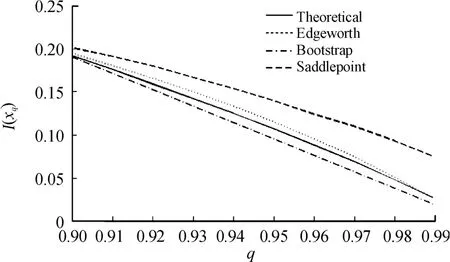
图1 样本量为20的gamma（5．5）分布的I（xq）真实值，Saddlepoint估计值，Edgeworth估计值以及Bootstrap拟合值

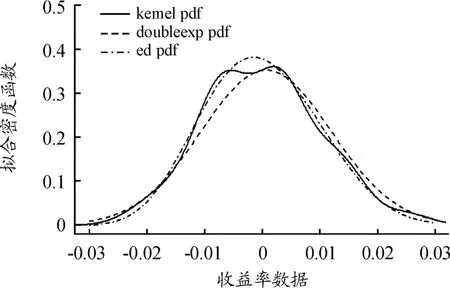
图2 收益率数据的拟合核密度函数图及其双指数分布和Edgeworth展开拟合的密度函数

从图2中看出：Edgeworth展开拟合的密度函数比Saddlepoint展开拟合的密度函数更接近参照值。进一步比较表2中VaR值的近似值，反转Lugannani Rice和Cornish Fisher估计在精确程度上相当，且相对误差都不超过15%。观察表3比较I（xq）的计算结果，Edgeworth展开更为精确，误差比不超过15%，优于Saddlepoint展开。

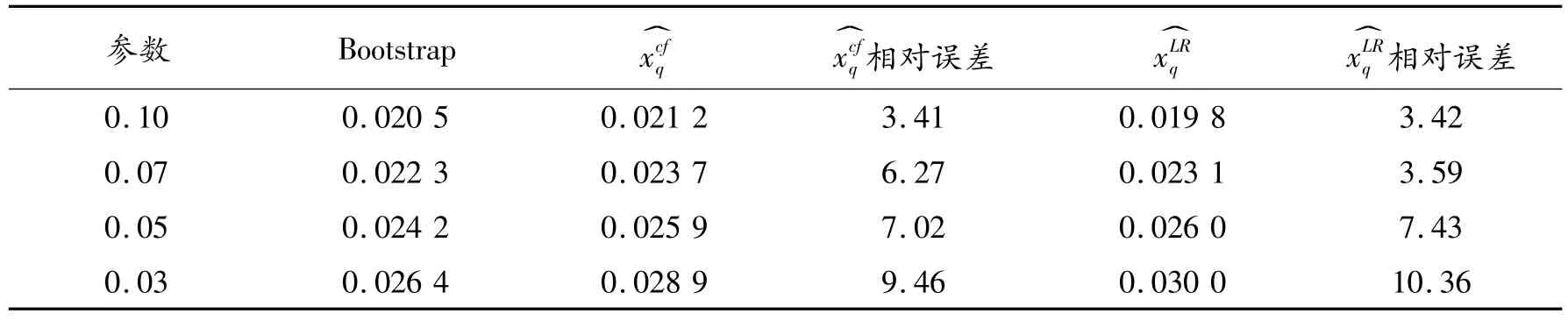
表2 3种方法在不同尾部概率下的分位数估计

表3 3种方法在不同的概率下计算的I（xq）值

4 结论

比较分析了在小样本情况下Edgeworth展开和Saddlepoint展开在计算ES值时的优劣。随机模拟和实证分析结果可以看出：Edgeworth展开计算更为简单、结果更为精确。Cornish Fisher展开和反转Lugan nani Rice公式都给出了VaR值的相对误差小于15%的有效估计值，相比之下反转Lugannani Rice没有一个具体的表达式，计算繁琐。需要指出的是，Saddlepoint展开是基于累积量生成函数得出的，如果分布的矩母函数不存在，则无法使用Saddlepoint展开。