具有Logistic输入和密度制约的一类阶段结构传染病模型
2021-02-28刘亭亭乔志琴
刘亭亭,乔志琴
(中北大学 理学院,太原 030051)
1 研究背景
研究传染病的发病机理、传染规律和防治策略是医学研究的重要内容[1]。然而在现实世界中,诸如麻疹、水痘、猩红热等传染病多见于幼年时期,白喉、淋病、性病等传染病则多见于成年阶段。因此,研究阶段结构的传染病具有重大现实意义。对于阶段结构的传染病,许多专家和学者已经进行了大量的研究[2-16]。文献[2-3]研究了单种群结构的模型,文献[4-8]主要研究了几类阶段结构的幼年患病传染病模型。文献[9-16]主要研究了几类阶段结构的成年患病传染病模型。
随着研究的深入,研究人员发现温度、食物、空间等都会引起种群数量的变化,由此提出了环境容纳量的概念,并引入了Logistic输入这一概念。幼年个体向成年个体的发展过程中,需要获取一系列的资源来保持自身的增长。当个体所需资源非常相似时,竞争就会相当激烈,出现种内竞争。由于分析的复杂性,很多模型在研究过程中都没有考虑密度制约[16]。
本文在前人研究的基础上,考虑并分析了一类具有Logistic输入和幼年受密度制约的阶段结构传染病模型。假设种群中个体生长分为幼年和成年两个阶段,疾病仅在成年种群中传播,幼年个体以Logistic形式输入,并受密度制约,而成年个体不受密度制约。x=x(t)、y=y(t)和z=z(t)分别表示t时刻幼年、成年易感者和成年染病者的数量,N(t)=x+y+z表示t时刻种群的个体总数量。假设所有参数均为正,其中参数r表示内禀增长率;K表示环境容纳量;d1、d2表示幼年个体、成年易感个体自然死亡率;d3表示成年染病者的移除率,包含自然死亡、因病死亡等;m表示单个幼年个体的平均成熟率;η表示幼年个体的密度制约系数;β表示疾病的传染率系数并建立以下传染病模型:

本文中侧重对初值(x(0),y(0),z(0))限定在集合D={(x,y,z)∈R3+|x>0,0<y≤K,z>0}上系统 (1)的解(x(t),y(t),z(t))的分析,其中t≥0。系统 (1)对应流程如图1所示。
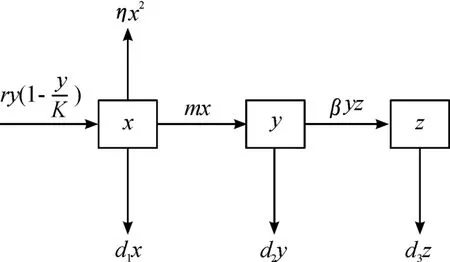
图1 疾病传播流程示意图
引理1 初始条件在D上系统 (1)的t≥0部分的解均为正的。

由以上结论可知,系统 (1)的初值落在D中,其解轨线均为正解。证毕。
引理2 系统(1)的一切正解最终有界。
证明:将系统 (1)的3个等式相加,并令d=min{d1,d2,d3},可以得到
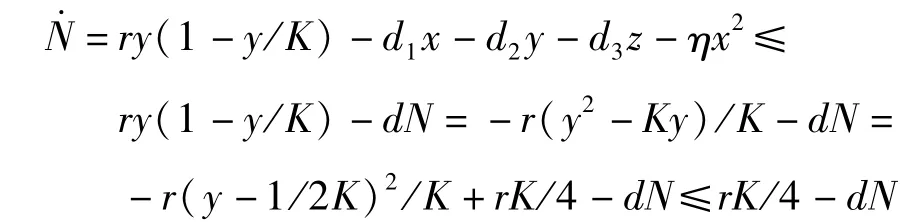
根据比较定理[17]可以得到 limt→+∞sup N≤rK/4d。所以对 ε>0,-T>0,当t>T时,x(t)<rK/4d+ε,y(t)<rK/4d+ε,z(t)<rK/4d+ε。因此,系统(1)一切正解最终有界。证毕。
2 平衡点的存在性分析
为了后续研究的方便,引入以下参数:

其中R0和Re0分别表示阶段结构种群的基本再生数和传染病的基本再生数,显然有Re0<R0。
定理1

证明:系统(1)的平衡点满足以下方程组:
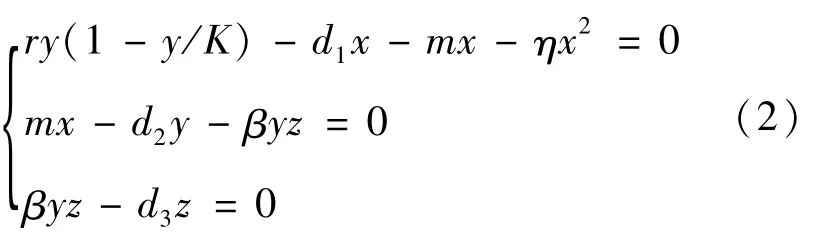
由第3式可得,z=0或y=d3/β。
当z=0时,代入方程组(2)的第2式知
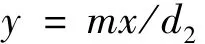
并由式(2)的第1式可得
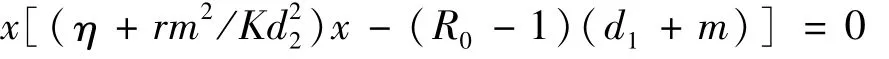
则可解得x=0或

且y0=mx0/d2。
当z≠0,y=d3/β时,由式 (2)第2式得
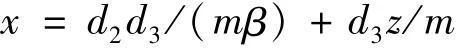
代入式(2)的第1个方程得到
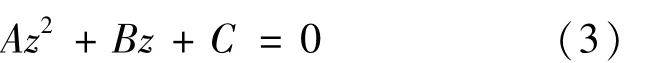
由于A,B>0,则仅当C<0即Re0>1时,式(3)有一正解,从而当且仅当Re0>1时,系统 (1)存在唯一的地方病平衡点E(x,y,z)。证毕。
3 平衡点的稳定性分析
定理2 当R0<1时,系统 (1)的平衡点E(0,0,0)局部渐近稳定;当R0>1时,系统 (1)的平衡点E(0,0,0)不稳定。
证明:系统(1)在E(0,0,0)处的雅克比矩阵为
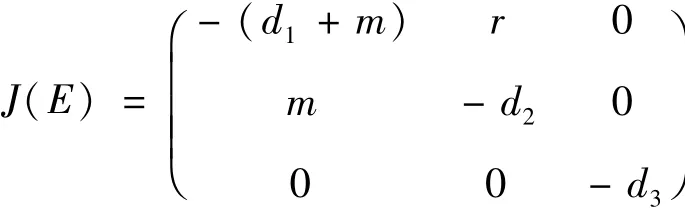
其对应的特征方程有1个实特征根λ1=-d3<0,另外2个特征根λ2,λ3满足方程:

所以,当R0>1时,方程 (4)具有1个正实根;当R0<1时,方程(4)的2个根均有负实部。证毕。
定理3 当R0≤1时,系统(1)的平衡点E(0,0,0)全局渐近稳定。
证明:构造Lyapunov函数
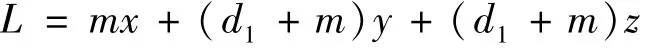
对L求全导数:
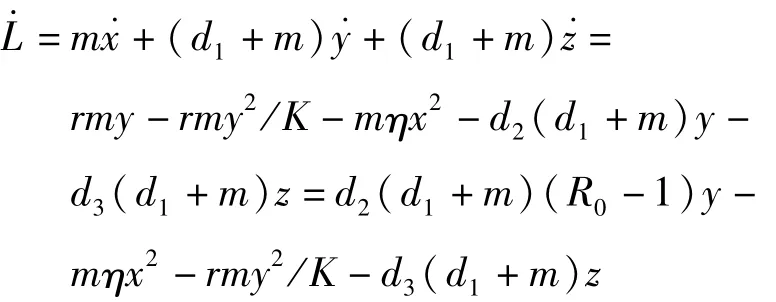
当R0≤1时,L·≤0;当且仅当x=y=z=0时,L·=0,系统 (1)在集合{(x,y,z)∈D∶L·=0}上的最大不变集是单点集{E}。根据LaSalle不变性原理[18]可知,E(0,0,0)全局渐近稳定。证毕。
定理4 当Re0<1<R0时,系统 (1)的平衡点E0(x0,y0,0)局部渐近稳定,而当Re0>1时则不稳定。
证明:系统 (1)在E0(x0,y0,0)处的雅克比矩阵为:
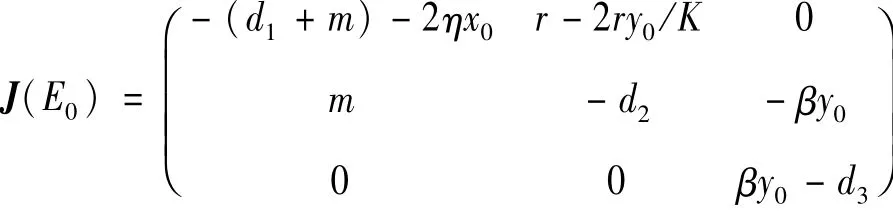
易知此矩阵对应的特征方程有1个实根:

当Re0<1<R0时,系统 (1)的平衡点E0(x0,y0,0)局部渐近稳定。证毕。
为了证明平衡点E0和平衡点E 的全局稳定性,首先给出以下命题。
命题1 令

可得F1(x,y)≤0,F2(x,y)≤0,其中(x,y)∈D。
证明:下面仅证明F1(x,y)≤0。F2(x,y)≤0类似。

1)在P01(x01,K)处的Hessian矩阵[19]为

3)在P0(x0,y0)处的Hessian矩阵为
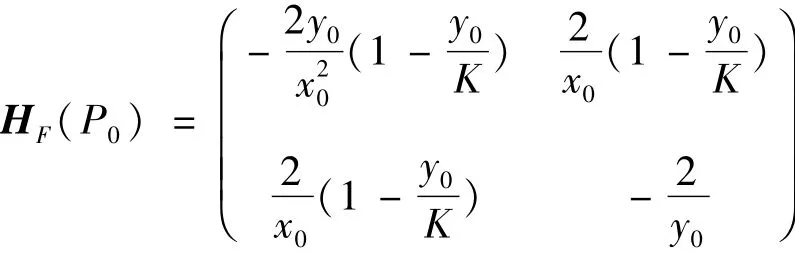
由系统(1)的第1个方程可知y0<K。因此

因此P01(x01,K)、P02(x02,K)均不是F1(x,y)的极值点。P0(x0,y0)为F1(x,y)惟一的极大值点,并在P0(x0,y0)处取得最大值,F1(x0,y0)=0,所以F1(x,y)≤0。证毕。
定理5 当Re0≤1<R0时,系统 (1)的平衡点E0(x0,y0,0)全局渐近稳定。
证明:构造Lyapunov函数,设
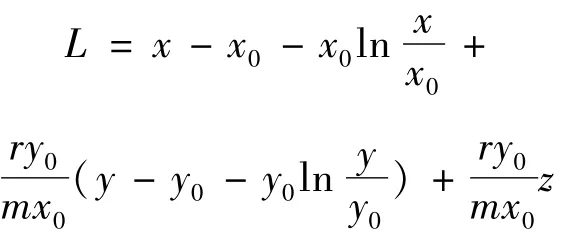
对L求全导数可化简为
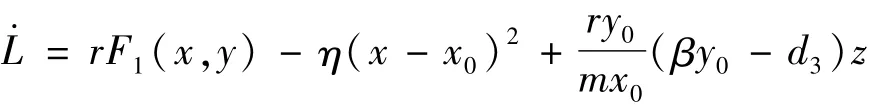
由命题1可得F1(x,y)≤0。当Re0≤1时,有βy0≤d3成立,则·L≤0;并且易知系统 (1)中{(x,y,z)∈D:·L=0}={E0};由LaSalle不变性原理知,当Re0<1<R0时,E0(x0,y0,0)是全局渐近稳定的。证毕。
定理6 当Re0>1时,系统 (1)的平衡点E(x,y,z)局部渐近稳定。
证明:系统(1)在E(x,y,z)处的雅克比矩阵为

矩阵的特征方程为

其中:
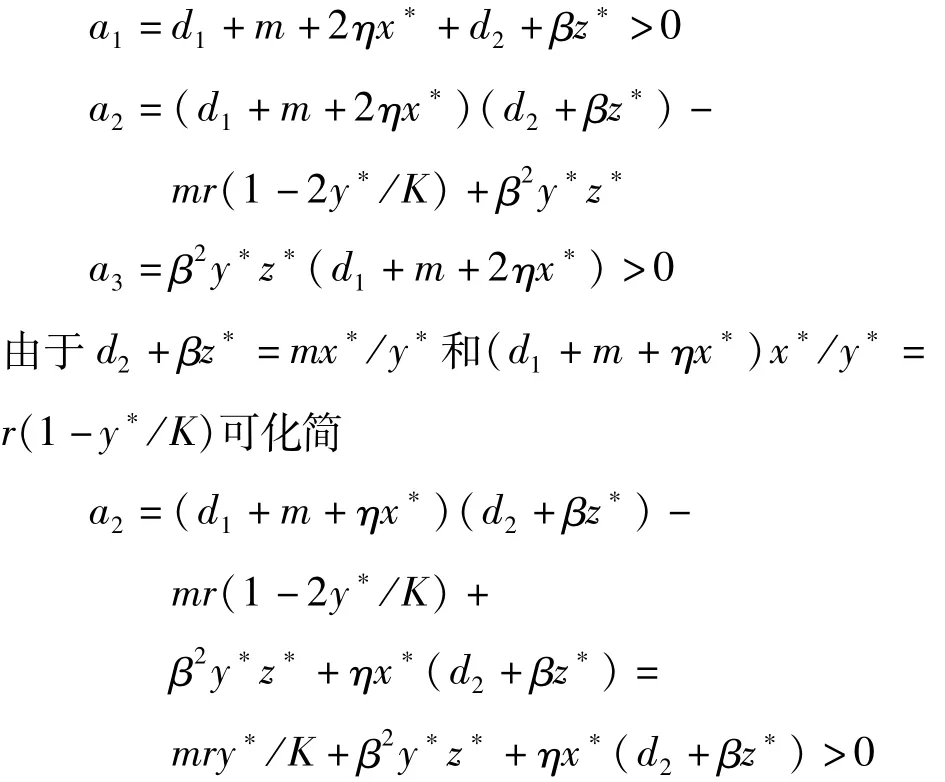
且有
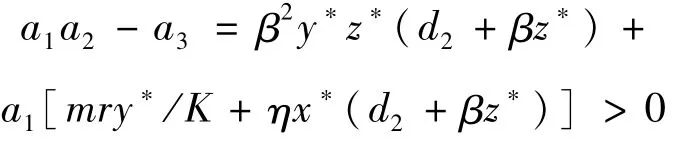
由Hurwitz判据[17]可知,J(E)对应的所有特征值均具有负实部。因此,系统 (1)的平衡点E(x,y,z)局部渐近稳定。证毕。
定理7 Re0>1时,系统 (1)的平衡点E(x,y,z)全局渐近稳定。
证明:构造Lyapunov函数,设

对L求全导数:

由命题1有F2(x,y)≤0,因此L·≤0;当且仅当x=x,y=y,z=z时,·L =0;系统 (1)在集合{(x,y,z)∈D:·L=0}上的最大不变集是单点集{E}。根据LaSalle不变性原理可知,当R >1
e0时,E(x,y,z)是全局渐近稳定的。证毕。
4 数值模拟
模拟系统(1)的无病平衡点和地方病平衡点,给出时间序列图和系统轨线图。
模拟1 取r=0.9,K=2,d1=0.25,d2=0.2,d3=0.5,m=0.1,η=0.01,β=0.2,则R0=1.286>1>Re0=0.468。选取初值x(0)=0.2,y(0)=0.1,z(0)=0.1,模拟平衡点E0(x0,y0,0)附近的渐近性态,如图2所示。任取5组初始值模拟Re0<1<R0时系统的轨线图,如图3所示。
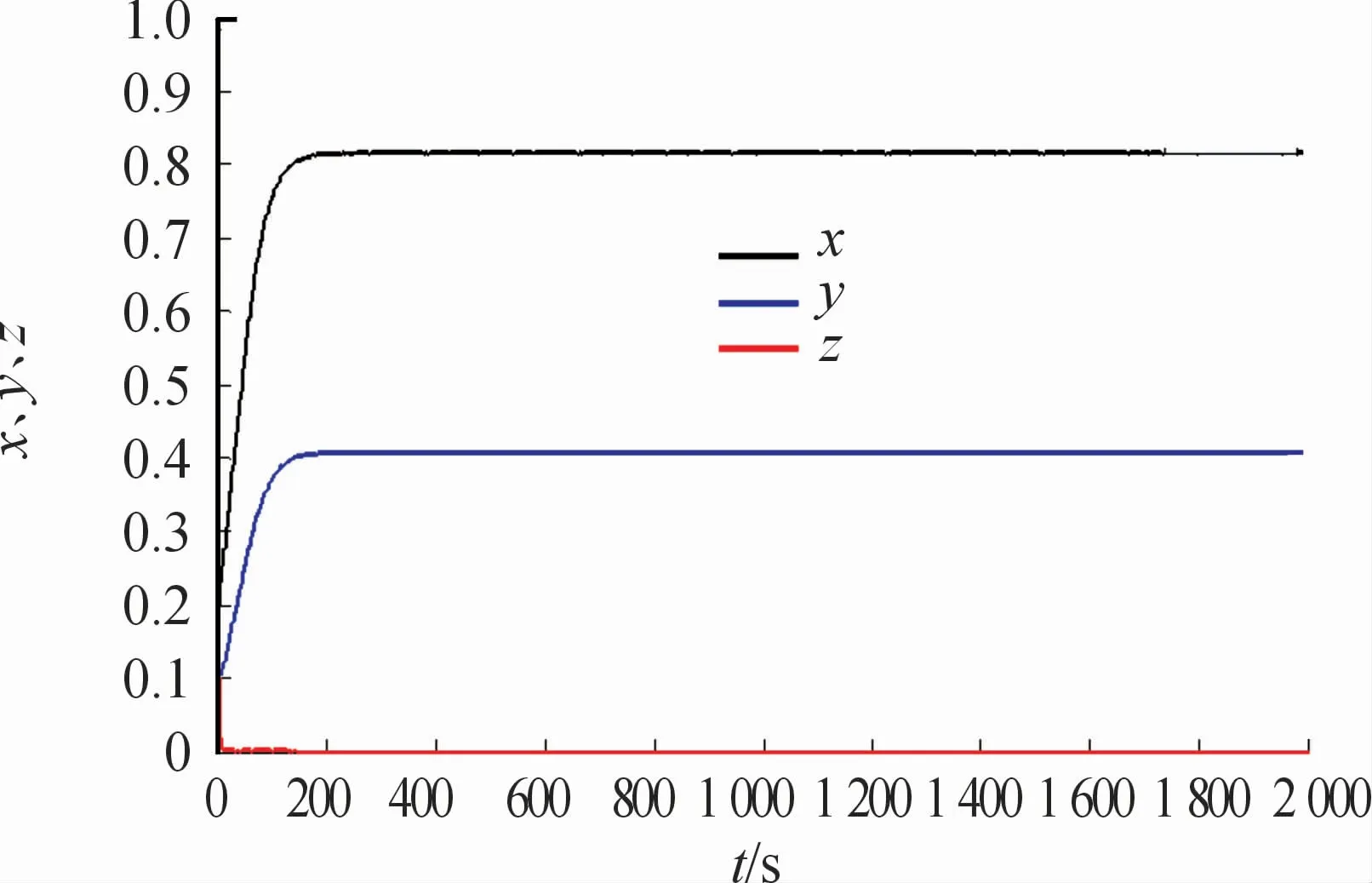
图2 无病平衡点E0随时间变化序列图
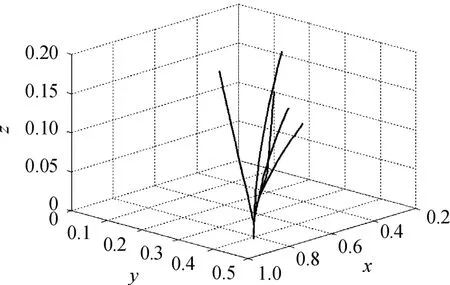
图3 Re0<1<R0时系统轨线图
通过数值模拟发现:当Re0≤1<R0时,曲线随时间变化最终趋于稳定,所以E0(x0,y0,0)是全局渐近稳定。
模拟2 取r=0.4,K=2,d1=0.05,d2=0.3,d3=0.01,m=0.3,η=0.3,β=0.2则R0=1.143>Re0=1.067>1。选取初值x(0)=0.3,y(0)=0.5,z(0)=0.1,模拟地方病平衡点E(x,y,z)的渐近性态,如图4所示。任取5组初始值模拟Re0>1时系统的轨线图,如图5所示。
通过数值模拟发现;当Re0>1时,曲线随时间变化最终趋于稳定,所以E(x,y,z)是全局渐近稳定。
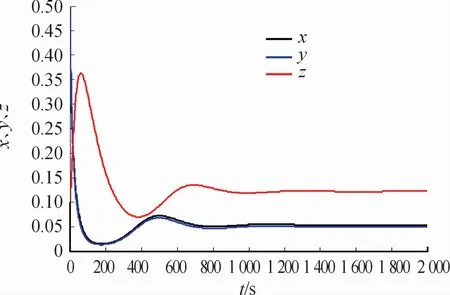
图4 地方病平衡点E 随时间变化序列图
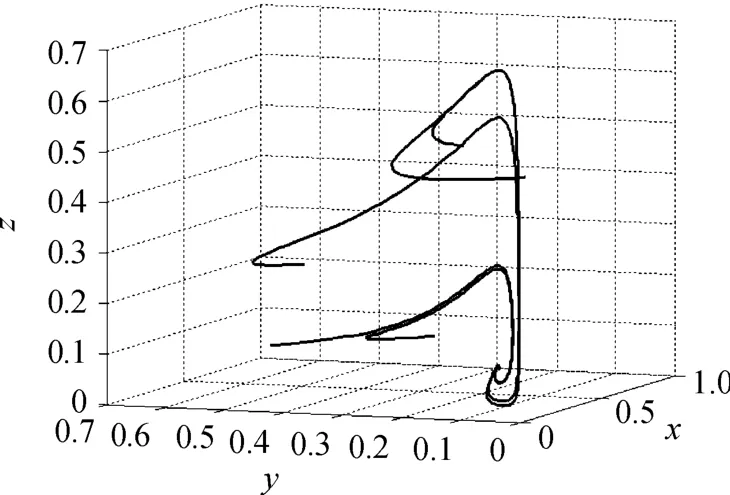
图5 Re0>1时系统轨线图
5 结论
在考虑Logistic输入和密度制约的情形下,分析了平衡点的存在性和稳定性,并利用Matlab进行数值模拟。此外,同时考虑幼年和成年均受密度制约的情形或在此基础上更加符合现实情况的疾病发生率等可作为下一步研究工作。
