颜色密度直方图检索方法
2021-02-28王小玲毛宏燕
王小玲,毛宏燕
1(上海立信会计金融学院 信息管理学院,上海 201620) 2(华东师范大学 上海高可信计算重点实验室,上海 200062)
1 引 言
由于数字媒体的爆炸式增长和图像的广泛应用,图像检索技术获得了长足的发展.基于内容的图像检索(CBIR)技术利用颜色、纹理以及形状或者组合特征,与目标图像进行比较.颜色特征一直是图像检索系统中最重要的描述符之一.颜色直方图(Color Histogram CH)方法自提出以来,以其旋转,缩放鲁棒性优点一直被广泛采用[1].然而,由于它只考虑颜色的总量,不能区分具有相同颜色数量但不同颜色分布的图像.
为了将图像的颜色信息和空间结构信息进行结合,许多研究试图从不同角度挖掘颜色的空间特征,提出了各种改进算法.大致可分为两类:1)从图像内颜色分布特点出发建立直方图.如较早的颜色相干矢量(CVV)[2]改进方法,它从颜色在图像中的自然分布着手,根据像素连通量的大小,把直方图分成两部分:相干的和非相干的,摆脱了全局颜色的约束.文献[3,4]通过k-均值聚类获取聚类图,然后统计基于空间位置分布的颜色直方图.文献[5]借助纹理、文献[6,7]依靠边缘提取颜色直方图,达到了间接反映颜色的空间特征的目的.2)基于分块的颜色直方图.这类改进算法在建立直方图之前,先对图像以不同方式分割,将图像的全局区域颜色特征划分成几个局部区域的颜色特征,从而反映空间位置信息.如文献[8-11]将图像分割为若干块,分别计算不同权重区域的颜色特征,利用每个块的颜色直方图搜索图像.这些改进人为划分区域,破坏了直方图算法原有的优点,而且区域的权重分配一直是一个难题,固定权值[11]或者通过反复实验得到的权值[12]缺乏灵活性,会影响检索结果的准确性.文献[13,14]提出利用颜色分布熵计算色彩的空间分布分散程度,以此作为分块加权系数.
本文提出了一种新的颜色密度的直方图(Color Density Histogram CDH).通过计算主要色彩的颜色密度,反映图像中占主导地位的颜色的色彩空间分布特点.实验结果证明,本文提出的CDH方法增强了传统直方图区分颜色空间分布差异的能力,提高了检索性能,达到了满意的效果.
第2节介绍了CDH的基本算法.第3节给出了图像相似性度量算法.实验在第4节中讨论.
2 算法描述
颜色直方图定义如下:给定颜色空间C,图像I的归一化颜色直方图H是:
HC(I)={N(I,Ci)|i∈[1,…,n]}
(1)
N(Ii,Ci)是落入Ci的颜色数量之和,i是颜色空间C的色彩等级.显见,颜色直方图只依赖于颜色总量而完全丢失颜色空间分布信息.如图1(a)、图1(b),由于像素总量相同,传统颜色直方图无法区分这两种情形.

图1 传统直方图失效情形
事实上,人们经常会使用“集中”与“分散”这样的词语区分图1(a)和图1(b)两种情形.如果能在直方图中,反映这种空间分布特点,就可以提高直方图检索性能.本文提出颜色密度直方图方法解决这一问题.给出颜色密度的定义:
ρc(I)={N(I,Ci)/Ai|i∈[1,…,n]}
(2)
其中,Ai是色彩等级为i的颜色在图像中所形成的区域的外接矩形的面积.那么,N(I,Ci)/Ai就是该区域的颜色i的密度,它能够反映颜色i的空间分布特点.ρc越趋于1,图像中色彩i的离散程度越小,也就是颜色分布越集中.反之,离散程度越大、越分散.这些像素形成的区域的外接矩形在图2中标出,其四个顶点的坐标分别是top_left,top_right,bottom_left 与 bottom_right,在图2(a)中标出.

图2 外接矩形示意图
显见图2(a)与图2(b)颜色密度的差异较大,可以作为区分二者的主要特征.有两种常见的多边形的外接矩形计算方法[15].一种是最小绑定矩形(Minimum Bounding Rectangle,简称MBR),即以多边形顶点中的最大、最小坐标确定的矩形.另外一种是最小面积外接矩形(Minimum Area Bounding Rectangle,简称MABR).本文的色彩密度计算精度要求不高,因此采用MBR方法,有利于提高计算速度.
根据获取的外接矩形的顶点坐标top_left,top_right,bottom_left与bottom_right,计算颜色i所形成的区域的外接矩形面积:
Ai=(top_right-top_left)*(bottom_right-bottom_left)
(3)
至此,我们获得了颜色空间C下图像I的特征描述:fC(I)={N(I,Ci),ρ(I,Ci)|i∈[1,…,n]}.
下面给出算法的主要步骤:
1)对颜色空间的每个像素值i,Seti=1,对其他像素值,Seti=0,完成二值化.
2)计算i=1像素数目N.
3)计算i=1所形成的区域的外接矩形面积Area.
4)计算颜色i的密度:N/Area.
3 相似性度量
在色彩空间C,基于获得的特征向量{N(I,Ci),ρ(I,Ci)|i∈[1,…,n]},采用欧氏距离构造相似性度量公式(4)如下:
(4)
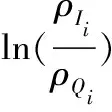
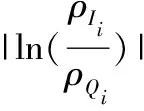
从公式(4)易知,对查询图像Q的某个颜色i而言,即使其数量较少,但只要数据库图像I的颜色分量i与其颜色密度趋势一致,就在相似性度量中与那些数量较多的颜色具有相近的重要性.然而事实上,我们知道,人眼在比较图像相似度时,更多是关注那些主要颜色,对于数量较少的颜色并不敏感.颜色直方图对形如图1(a)的检索效果是最好的.为了保留这种优势,本文提取图像中数量较多的若干颜色代表一幅图像的主要色彩.做到既考虑主要色彩,又考虑颜色分布特点,从而减少那些数量较少的颜色对检索性能的干扰.
4 实验与分析
4.1 算法评价
查准率(Precision)和查全率(Recall)是普遍采用的两个检索性能评价准则,分别代表检索的速度和成功率.记{Relevant}是与查询图像相关的图像,{Retrieved}是系统检索出的图像.则既相关又被检索出的图像记为:{Relevant}∩{Retrieved}.
查准率(Precision)是检索到的图像中与查询相关的图像所占百分比,其定义如式(5)所示:
(5)
查准率反映系统拒绝无关图像的能力.
查全率(Recall)是与查询图像相关且被实际检索出的图像的百分比,其定义如式(6)所示:
(6)
查全率反映系统检索相关图像的能力.查准率和查全率越高,说明算法的检索性能越好.
4.2 HSV颜色空间及其量化
由于RGB彩色图像的颜色特征维数过高,本文采用与人眼视觉特征更加一致的HSV(Hue Saturation Value)颜色空间,并采用文献[16]的方法,将其量化为72种颜色,既可以满足肉眼分辨色彩的要求,又可以降低直方图的计算量,提高检索效率.
从RGB颜色空间到HSV颜色空间的转换具体公式如式(7)-式(9)所示:
(7)
(8)
v=max
(9)
其中,max=max(R,G,B),min=min(R,G,B)r,g,b∈[0,1],h∈[0,360],s∈[0,1],v∈[0,1].
量化公式:
G=9H+3S+V
(10)
根据式(10),G∈[0,71],即HSV色彩空间被量化为一个72bin的空间.
4.3 实验数据库
本文采用Corel-1000数据库,该数据库主要有原始部落、海滩、公共汽车、花朵、恐龙、建筑等共计10个类别的彩色图像,每类100幅.
4.4 实验结果与分析
为了验证算法的有效性,本文对1000幅图像,在HSV空间,与传统直方图和文献[8]算法进行比较试验.传统直方图度量采用欧氏距离,颜色密度直方图采用公式(4)计算.按照第3节的分析结果,实验取前10,20,30,40,50,60,72个主要色彩,其前40幅图像的查全率性能比较如图3所示.显见,在本文采用的数据库上,取前20个数量最大的颜色检索性能最好,本文因此采用这种方案.
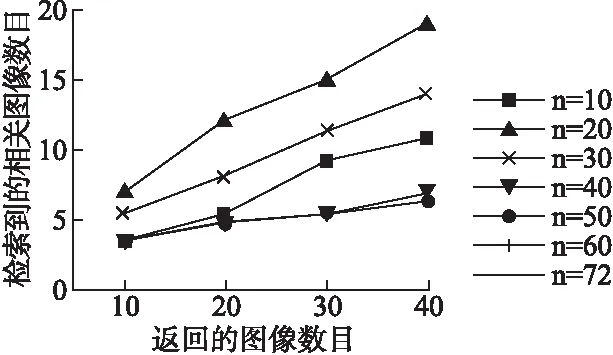
图3 不同主颜色数目查全率比较
从图4可见,与传统直方图和文献[8]算法相比,本文提出的颜色密度直方图检索效果显著提高:颜色直方图检索出10幅相关图像,文献[8]检索出13幅相关图像,CDH检索到18幅相关图像,且相关图像排序靠前.如果进一步严格区分,CDH且检索到了14幅含有纪念碑形状的图片,而文献[8]与CH分别均检索到4幅和5幅(图4内使用黑色矩形框框出).这表明,本文提出的算法抓住了颜色的空间分布特点,较好地排除了数据库中海滩图像类别内的100幅图像对检索结果的干扰,表达了纪念碑这部分对象的空间分布特点,提高了检索性能.

图4 HSV空间CH(a)与文献[8](b),CDH(c)检索实例
图5给出了HSV颜色空间下,CDH与CH、文献[8]的检索性能比较.图像库中相似图像总数为100.CDH在这3种算法中,检索性能最优,其平均查准率较CH提高21%,平均查全率提高25%.
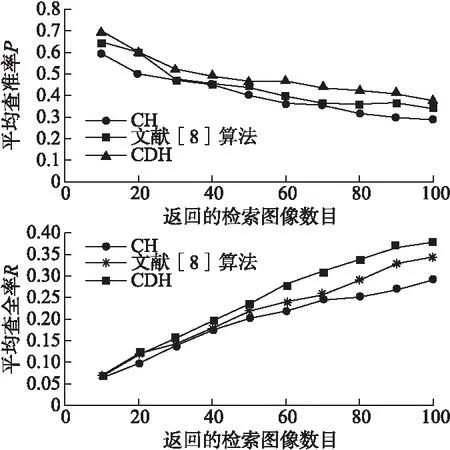
图5 HSV空间检索性能比较
传统直方图检索方法依赖像素数量这一单一指标度量相似度,本文引入其所形成的外接矩形面积这一指标,增加了算法区分度.理论上存在颜色密度值相近而实际分布存在差异的情况.我们知道,同类对象其形状外观具有一定的稳定性,因此这些色彩所形成的面积也具有稳定性.不同类图像出现面积相似的概率随之降低.在本文所选择的数据库内,以花朵类中的红色花朵(17幅)与公共汽车类的红色公交车(33幅)作比较,二者共同的特点是红色占主要部分,图6给出了其72bin颜色密度直方图比较,显见这两类图像自身存在一定的差异.
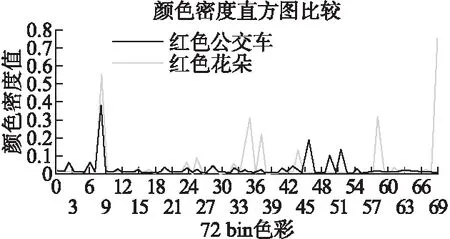
图6 不同类别图像的CDH比较
另外,本文采用的是前20个较大颜色分量,而不是所有色彩,也削弱了可能出现的颜色密度相似的分量在相似性比较中的地位.
上述两个因素,增加了本算法的可行性.
5 结 论
颜色直方图因具有图像旋转、缩放不变性优点,在图像检索中被广泛采用.但由于无法识别空间分布差异,导致性能下降.本文从颜色在图像内的自然分布状态出发,寻找能够反映空间分布的信息,使用颜色密度反映这种差异,提出颜色密度直方图,可以较好地改善上述不足.实验结果表明.该算法在保留传统颜色直方图优点的同时,可以显著提高检索性能.
