改进灰狼群优化算法的环境污染物预测研究

马占飞，江凤月，李克见，巩传胜

1(内蒙古科技大学 包头师范学院，内蒙古 包头 014030) 2(内蒙古科技大学 信息工程学院，内蒙古 包头 014010)

1 引 言

草原作为北方重要的国土资源，在人类的生产活动和自然环境的改善中发挥着不可替代的作用.近年来，随着人口的急剧增长和经济的快速发展，草原地区的大气环境受到严重的污染，造成大面积的草原退化和沙漠化现象.因此，准确预测草原污染物的浓度，对科学治理大气污染，维持草原生态系统的平衡具有重要的意义.在污染物预测研究中，群体智能优化神经网络的算法颇受研究学者青睐.灰狼群算法[1]，是新型的群体智能优化算法之一，国内外的学者们在此基础上进行了不同的探索.例如，文献[2]通过遗传算法优化的RBF神经网络的算法，建立RBF-GA的预测模型证明预测精度有所提高;文献[3]建立了基于径向基函数(RBF)神经网络的预测模型，并用粒子群算法(PSO)对神经网络的参数进行优化;文献[4]通过与GWO优化的SVM算法、遗传算法优化的SVM、粒子群算法优化的SVM预测算法相比，发现改进的GWO优化SVM的算法预测精度更准确;文献[5]建立基于灰狼群智能优化神经网络的预测模型，证明了此预测模型具有较好的泛化能力;文献[6]证明了在非线性问题的计算中，RBF神经网络有良好的的逼近能力;文献[7]通过与粒子群优化算法、人工蜂群优化算法相比较，证明所提出的灰狼群算法是一种很高效的优化算法;文献[8]利用群体智能优化算法调整RBF神经网络的学习参数，提高了算法的收敛速度;文献[9]利用灰狼群算法，优化RBF神经网络的学习参数，进而提高了RBF神经网络对非线性问题的处理能力;文献[10]利用改进的灰狼群算法，证明此算法在径向基网络逼近上有全局优化的优势;文献[11]提出了对数函数描述收敛因子的改进GWO算法，避免灰狼群算法在求解复杂问题易陷入局部最优的问题;文献[12]通过非线性收敛和位置更新策略对基本灰狼群优化算法进行改进，得到了最优结构参数证明了该模型模型结构简单，预测精度较高.

通过以上文献可知，灰狼群算法优化RBF网络对于非线性预测研究，有良好的预测性能.但传统的GWO算法寻优能力不足，容易陷入局部最优，而大多数的研究只利用灰狼群算法优化权值，而忽略了聚类中心参数的学习优化，从而导致预测算法精度不高，泛化能力弱的问题.本文通过最近邻聚类算法调整聚类中心，再结合改进后的GWO算法优化权值参数，避免了以上问题，并用草原地区的实例验证了该预测算法的有效性和合理性.

2 传统RBF神经网络

径向基神经网络(Radial Basis Function Neural Networks，RBFNN)是一种使用径向基函数作为激活函数的人工神经网络[13].如图1所示.

图1 RBF神经网络结构

(1)

(2)

其中，‖Xp-Cl‖表示Xp与Cl之间的欧氏距离，Cl为第l个隐含层节点的聚类中心，r为宽度常数，nr表示隐含层节点的数目;Wjl是第l个隐含节点到第j个输出节点的连接权值，输出矩阵表示为：

Yp=W*hp=

3 优化RBF网络的学习参数

3.1 最近邻聚类调整中心参数

目前，调整RBF神经网络的中心参数的算法有很多，其中典型的算法为最近邻聚类算法(Nearest Neighbor Clustering Algorithm，NNCA).文献[14]证明了在调节RBF神经网络的参数学习中，隐含层的节点个数不需要事先确定，它能在训练当中自适应调节.最近邻聚类算法不仅能减少对聚类中心初值的依赖，而且能动态调整隐含层节点的数目，这样缩短了网络训练的时间.最近邻聚类算法描述如下：

算法1.NNCA调整聚类中心的算法描述

输入：样本数据集(Xp，Yp)，宽度常数r

输出：最近邻聚类中心Cl，权值向量W，隐含层节点数目nr

1.定义g为存放各类输出的矢量之和，b为统计各个聚类的样本个数，W为聚类中心Cl到输出层的权值向量

2.首先选择第一个样本(X1，Y1)作为初始聚类中心，nr=1，C1=X1，g=Y1，b=1，W=g/b

3.forp=2 toNdo：

4.forl=1 tonrdo：

5.计算样本Xp到l个聚类中心的欧式距离d=‖Xp-Cl‖

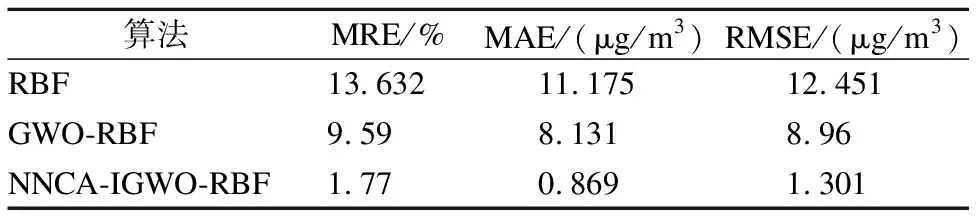
6.ifd

7.更新最小的欧氏距离mind=d

8.end if

9.end for

10.ifmind<=r

11.没有产生新的聚类中心，nr的数目不变，g=g+Yp，b=b+1，W=g/b

12.else

13.nr=nr+1，产生新的聚类中心Cnr，g=Yp，b=1，W=g/b

14.end if

15.end for

16.结束处理

3.2 改进灰狼群优化算法

3.2.1 灰狼群算法

灰狼群算法(Grey Wolf Optimization，GWO)是一种模拟灰狼群体捕食行为的新型智能优化算法.GWO算法具有结构简单、需要调节的参数少、简单易用等特点，其中能够在局部寻优与全局搜索之间实现平衡，因此在对一些非线性求解问题的精度和泛化能力方面都有良好的性能[15].为此，本文将利用灰狼群算法对RBF网络的权值参数进行优化.

在GWO算法中，将狼群分为从高到低的4个等级，将根据适应度值的大小排序，适应度值最优的灰狼为α，次优灰狼为β，第3优灰狼为δ，剩余灰狼为ω.在狼群捕获猎物的过程中，首先将选择适应度值最优的3匹灰狼α、β、δ进行猎物的追捕，而剩余灰狼ω将跟随前3匹灰狼α、β、δ进行围攻，最后猎物的位置为优化问题的解.

灰狼群的捕食行为可以分为包围、猎捕、攻击猎物这3个过程.

1)包围

在狼群的捕食过程中，狼群对猎物首先采用包围的行为.与灰狼群算法的寻优过程相对应，先计算灰狼个体Xi(t)与猎物Xp(t)之间的距离D，而第i只灰狼Xi(t)包围猎物Xp(t)的行为为Xi(t+1)，其对应的数学模型有：

D=|C·Xp(t)-Xi(t)|

(3)

Xi(t+1)=Xp(t)-A·D

(4)

A=2ar1-a

(5)

C=2r2

(6)

(7)

其中：式(4)为灰狼的位置更新公式;Xp(t)为猎物第t代时的位置向量;Xi(t)为灰狼个体第t代时的当前位置;A、C为系数向量;t为当前的迭代次数，ɑ为收敛因子，ɑ随着t的增加从2线性递减到0;r1和r2为[0，1]之间的随机向量;tmax为最大迭代次数.

2)猎捕

当灰狼判断出猎物的位置时，需要灰狼向猎物移动，其中灰狼β、δ在灰狼α带领下引导狼群ω对猎物采取包围行动，由于灰狼α、β、δ的位置是最靠近猎物的，所以将利用这3匹狼的位置判断猎物的位置，逐渐向猎物移动，进行猎捕.对应的数学模型有：

Dα=|C1·Xα(t)-Xi(t)|

(8)

Dβ=|C2·Xβ(t)-Xi(t)|

(9)

Dδ=|C3·Xδ(t)-Xi(t)|

(10)

其中，Dα，Dβ和Dδ分别表示α、β和δ与其他个体间的距离;Xα(t)，Xβ(t)和Xδ(t)分别代表α、β和δ的当前位置;C1，C2，C3是随机向量;Xi(t)是当前灰狼群体的位置.

X1=Xα(t+1)=Xα(t)-A1·Dα

(11)

X2=Xβ(t+1)=Xβ(t)-A2·Dβ

(12)

X3=Xδ(t+1)=Xδ(t)-A3·Dδ

(13)

(14)

其中：前3个式子分别定义了狼群中ω个体朝向α、β、δ前进的步长和方向，Xi(t+1)是ω的更新位置即最终群体历史最优解.

3)攻击

最后一个过程为攻击阶段，狼群需要完成抓获猎物这一目标，即灰狼群算法获得最优解.通过前两步可知，ɑ有着调节算法的全局搜索与局部开发的作用.在迭代过程中，当ɑ的值从2线性下降到0时，其对应A的值也在区间[-ɑ，ɑ]内变化.当│A│≤1时，狼群才能攻击猎物(陷入局部最优)，这样GWO算法才有良好的局部开发能力.当│A│>1时，包围区域扩大，灰狼群能分散开搜索猎物更可能的位置，这就形成了全局搜索.

3.2.2 非线性调整收敛因子

大多数的群智能优化算法中普遍存在着共同的问题：局部开发性能与全局搜索性能的调节问题.由上一节公式(7)可知，ɑ在迭代的过程中，由2线性递减到0，但是结合实际优化情况看，GWO算法的搜索过程很复杂，收敛因子ɑ线性递减的策略不能体现实际优化的过程，所以收敛因子ɑ应该采用非线性变化策略.

文献[16]中提出用正弦三角函数来改进收敛因子，即：

(15)

文献[17]中提出了用正切三角函数来改进ɑ的策略公式，即：

(16)

然而，该公式的收敛因子ɑ能达到非线性变化，但是围猎的区间和非线性变化不是很理想，A的变化也会受到影响，同时会影响全局的搜索能力.针对上述不足情况，受PSO算法的启发，和sin函数在[π/2，π]区间上非线性的递减的影响，本文将提出一种基于sin的收敛因子ɑ迭代公式，即：

(17)

其中，ɑinitial和ɑfinal表示收敛因子ɑ的初始值和最终值，本文取ɑinitial=2;ɑfinal=0;t为当前的迭代次数，tmax为最大迭代次数，ε为非线性调节参数，(ε>0).而且上述改进公式相对于公式(15)的区间减小了一半，公式(15)的改进虽然使ɑ在规定的区间[π/2，π]内非线性的变化，但在[0，π/2]区间上sin函数是非线性增加的，所以在进化过程中按照上述公式(17)进行优化，更符合收敛因子ɑ的实际变化.

3.2.3 适应度加权调整位置更新

由上一节的公式(11)-公式(14)可知，群体中的其他灰狼个体ω是根据当前最优的3头狼进行更新其位置，可以看出标准的GWO的位置更新只有好的开发能力而忽略了搜索能力，所以需要改进位置更新公式来协调群体和个体对GWO的搜索能力，以及保证狼群能快速有效的跳出局部最优，从而提高了GWO的寻优能力.

文献[18]可知，提出了加权距离灰狼群优化算法，利用最佳位置的加权总和来改进位置更新公式，即：

(18)

(19)

(20)

(21)

(22)

(23)

ω1=A1·C1，ω2=A2·C2，ω3=A3·C3

(24)

(25)

文献[19]可知，为了进一步加快算法的收敛速度，提出了一种适应度加权的位置更新公式，权重不再是固定的1/3，而是通过当前最优的3匹狼的适应度来更新权重.即：

(26)

(27)

其中，fα，fβ，fδ分别为α、β、δ当前的适应度.

通过以上文献，可以看出适应度加权的位置更新更适合GWO算法优化过程的进行，适应度在优化过程中有着很重要的作用，利用当前最优的3匹狼的适应度来更新权重，3者的适应度不同也能表现出不同的贡献度，不再是标准的GWO的固定权重.最后不管怎么迭代，灰狼群体不再受历史狼群的影响，更符合狼群的多样性的原则.所以本文利用文献[19]的适应度加权和受PSO算法的粒子位置的影响，提出一个适合本研究的适应度加权位置更新公式如下：

(28)

(29)

(30)

f=fα+fβ+fδ

(31)

在猎捕过程，是由当前3个狼的位置信息，更新其他狼个体ω的位置Xi(t+1)，而在整个GWO算法优化过程中，是根据适应度函数的值来比较确定前3个α、β、δ狼的位置信息，所以可以用当前3个狼的适应度值加权作为3个α、β、δ狼的位置系数，来更好的反应灰狼群的多样化，从而使GWO算法的开发能力和搜索能力更好的协调.其中，μ为很小的数，在本文将取值0.01，来防止样本输出的误差为0，minRi为目标函数，MSEi为第i个个体对应的目标误差函数，MSEi的值越小代表预测精度越高，而fi为第i个个体的适应度函数.在这里引入目标误差函数，用所有样本的均方误差(1+Ri)的倒数来代表个体的适应概率即fi.由于本改进算法中适应度的大小代表灰狼个体的位置优越度，适应度大的灰狼个体的位置代表最优解.

3.3 NNCA-IGWO优化RBF网络的预测算法

综上所述，本文提出新的优化RBF网络的预测算法，记为NNCA-IGWO-RBF预测算法.

算法2.NNCA-IGWO-RBF预测算法的描述

输入：高斯函数的宽度r，种群规模SN，最大迭代次数tmax，收敛因子的初始值ɑinitial和终止值afinal，非调节参数ε，当前迭代次数t，μ

输出：聚类中心Cl、新的权值和新的RBF模型结构

1.通过算法1构建RBF神经网络的聚类中心Cl，初始权值W

2.将待优化的权值参数W=[W11，W12，…，W1nr，W21，W22，…，Wmnr]映射为人工狼群的位置向量{Xi，i=1，2，…，SN}

3.计算群体中每个个体的适应度值{f(Xi)，i=1，2，…，SN}，通过比较产生当前最优个体α、次优个体β以及第3优个体δ，确定其对应的位置Xα、Xβ和Xδ

4.while(t

5.fori=1 toSNdo：

6.forj=1 tom*nrdo：

7.根据式(17)计算收敛因子ɑ的值

8.根据式(5)和式(6)计算A和C(系数)的值

9.根据式(30)更新个体ω的位置

10.end for

11.end for

12.计算群体中的个体的适应度值{f(Xi)，i=1，2，…，SN}，更新α、β和δ对应的位置Xα、Xβ和Xδ

13.t=t+1

14.end while

15.将Xα映射为权值矩阵W

16.构建新的RBF神经网络结构模型

17.结束处理

4 实验结果与分析

4.1 实验数据的选取和处理

草原环境的污染主要受周边环境污染物的影响，本文将利用NNCA-IGWO-RBF预测算法，对赛汗塔拉城中草原的首要污染物(PM10)进行建模预测.因此，选择最近的包头市环境监测站，能监测到草原环境的周边污染物数据[20].本文的实验数据将选取该站点从2018年1月1日-2020年5月31日期间的数据，在此之前需要对离散的原始数据进行24h均值处理.污染物数据来源于空气质量历史数据网(1)https：//quotsoft.net/air/;气象数据来源于天气网(2)https：//weather.com.cn/.从均值处理后的数据可以看出，初步预选的特征因子：污染物因素(PM2.5、PM10、SO2、O3、CO、NO2)，气象因素(风速、温度、湿度)，如表1所示.

表1 预选特征因子的描述

表1为初步预选因子的汇总，包括：前1天24h均值处理的PM10、PM2.5、SO2、O3、CO、NO2浓度值，前2天24h均值处理的PM10、PM2.5、SO2、O3、CO、NO2浓度值，当天24h均值处理的PM2.5、SO2、O3、CO、NO2的浓度值，当天的风速，当天的湿度，当天的温度.

为了解决实验数据x的数量级统一，在算法训练之前进行归一化处理，将数据归一化到区间[0.2，0.8]作为样本数据，同时使神经网络在训练当中，避免了出现神经元饱和的现象.归一化公式如下：

(32)

式(32)中x′为归一化后的数据，xmax、xmin为各项原始数据序列中不同时间内的最大值、最小值.

4.2 特征因子的降维处理

针对影响目标因子(PM10_24h)的预选特征因子，通过Pearson相关分析法进行相关系数的分析，确定更有代表性的输入因子.Pearson用来分析筛选特征因子和目标因子的相关性强弱，其绝对值的范围在[0，1]之间.其中相关系数的绝对值越大，相关度越强，相关系数越接近于1或-1，相关度越强;相关系数越接近于0，相关度越弱.假设2个变量元素{x，y}，变量x与变量y的相关系数公式为：

(33)

表2 PM10_24h与20个预选特征因子的相关系数矩阵

由表2可以知，将选择显著相关、高度相关、中度相关的特征因子R1、R4、R7、R10、R13、R18、R19、R20作为RBF神经网络的输入因子，而剔除低度相关、微弱相关的特征因子.

4.3 算法性能的评价指标

本文将通过平均相对误差(Mean Relative Error，MRE)、平均绝对误差(Mean Absolute Error，MAE)和均方根误差(Root Mean Squared Error，RMSE)3种指标，来确保更好地分析算法的预测性能.将利用获取的771组训练集数据进行预测模型的训练，对110组测试集数据进行验证预测模型的精确度，其计算公式分别如下：

(34)

(35)

(36)

4.4 结果分析

将以8个具有代表性的特征因子为预测模型的输入因子，而当天的PM10_24h浓度值为输出因子，即在构建草原环境污染物的预测模型中，输入节点数为8个，输出节点数为1个，即NNCA-IGWO-RBF预测模型结构为8-nr-1，网络结构图如图1所示.在此预测模型中，首先对归一化后的样本数据进行分组，共采集881组实验数据，其中771组为训练集数据，通过NNCA-IGWO-RBF预测算法进行模型的参数(Cl，W，r)的训练;而110组测试集数据进行验证模型的性能，从而得到更稳定的预测模型.在NNCA-IGWO-RBF网络训练中，宽度常数r需要事先确定，通过大量的实验对比，确定r的取值为0.3;其中最大迭代次数tmax=150，种群数量SN=80，初始值ɑinitial=2和终止值afinal=0，ε=2，t=0，μ=0.01.通过测试集验证该模型，预测的结果与真实值的拟合情况，如图2所示.

图2 PM10_24h真实值和预测值的比较

从图2可知，NNCA-IGWO-RBF算法的预测值与真实值的大部分样本拟合度较高，个别的样本拟合度较小，其中平均相对误差为1.77%，平均绝对误差为0.869μg/m3，最大的绝对误差为6.133μg/m3，最小绝对误差为0.003μg/m3，均方根误差为1.301μg/m3.

为了进一步地验证NNCA-IGWO-RBF算法的预测性能，将其与传统RBF、GWO-RBF的预测算法进行对比，结果如表3所示.

表3为以上3种不同算法在平均相对误差MRE、平均绝对误差MAE、均方根误差RMSE的预测性能对比情况.传统的RBF算法对PM10_24h浓度预测值和实际值拟合度不高，它们在RBF网络的学习参数调节上，易出现学习参数多而难以调节，使RBF网络陷入局部最优;与GWO-RBF算法、NNCA-IGWO-RBF算法相比，其预测的误差较大.而对于GWO-RBF预测算法，其结果的预测误差相对较小，但预测性能并没有得到明显的改善，是因为GWO-RBF预测算法只利用GWO优化RBF的权值参数，忽略了RBF网络的聚类参数也容易学习不足，从而导致了其预测精度低，泛化能力弱.NNCA-IGWO-RBF算法的MRE为1.77%、MAE为0.869μg/m3、RMSE为1.301μg/m3，这3个值和其他两种预测算法相比，其预测误差最小，预测效果明显提高，是因为利用最近邻聚类算法(NNCA)优化RBF网络的聚类参数，然后再利用IGWO算法优化其权值参数，从而达到共同调节RBF网络学习参数的优化问题.其中，3种不同算法的预测结果和真实值的拟合情况，如图3所示.

表3 不同算法的预测性能对比

图3 3种不同算法的PM10_24h浓度预测对比

从图3对比分析可知，NNCA-IGWO-RBF预测算法在PM10_24h浓度预测上要优于其他两种预测算法.因此，本文提出的预测算法对PM10_24h浓度期望值拟合度更高，且预测误差最小，说明NNCA-IGWO-RBF算法的整体预测结果更精确，且具有很好的泛化能力，在此说明对于草原环境污染物的预测有一定的实用性和有效性.

5 结束语

本文提出一种组合最近邻聚类算法(NNCA)和改进灰狼群(IGWO)优化RBF神经网络的预测算法.该算法通过最近邻聚类算法调整RBF神经网络的聚类中心参数，然后利用改进的GWO算法调整RBF神经网络的权值参数，从而共同优化RBF网络的学习参数.最后将优化后的算法应用于城中草原环境污染物PM10的预测中.结果表明，与其他2种算法相比，该算法的预测误差最小，预测精度较高且泛化能力强，具有一定的实用性和有效性.但是在预测过程中，其他气象因素(天气状况、压强等)也对PM10有所影响，后续有待进一步研究.