一种嵌入式计算平台的Sigmoid函数优化方法

林钰棽，魏云龙，陈琪琪，张 威，邱志敏

1(福州大学 物理与信息工程学院，福州 350100) 2(华南理工大学 电子与信息学院，广州 510640) 3(中国科学院大学 中国科学院长春光学精密机械与物理研究所，长春 130033) 4(北京航空航天大学 电子信息工程学院，北京 100191)

1 引 言

人工智能及边缘计算的大规模应用，使人工神经网络(Artificial Neural Network，ANN)在端侧的应用日益广泛.端侧计算常用的处理器为嵌入式处理器，神经网络在资源受限的嵌入式处理器上的计算效率不高.Sigmoid函数是人工神经网络常用的激活函数，其计算过程需要进行指数和除法运算，其较高的计算时间复杂度和空间复杂度影响嵌入式平台的神经网络计算效率，提高Sigmoid函数计算效率是当前嵌入式计算平台提高神经网络运行效率需要解决的关键问题之一.

Sigmoid 函数主体为e指数运算，常用标准C的math库exp函数实现，分析其源码可知其实现原理为泰勒级数展开法1.为了提高精度，泰勒级数展开法往往需要高阶展开，这样增加了Sigmoid函数的运算复杂度和计算资源的消耗.为了降低Sigmoid函数运算复杂度，目前已提出了如查表法、CORDIC 算法、多项式拟合等方法.

查表法将不同x值所对应的Sigmoid函数值存储在已知存储块中，计算时根据输入变量在已存变量存储块中查找该变量对应的计算值，进而得到计算结果.随着精度的提高所需的存储资源显著增加，资源消耗高[1].CORDIC算法即坐标轴旋转数字计算方法，其本质是通过一系列与运算有关的角度基底θk来逼近任何一个旋转角度.该计算只需简单的移位和加减，不涉及乘除，但其本质是迭代收敛算法，计算时间长，且实时性差[2].多项式拟合法即将Sigmoid函数分段，每段采用合适的折线段来逼近Sigmoid函数[3-7].该方法对拟合函数有较高的要求，使用低阶多项式会使精度降低，而高阶多项式则会增加运算复杂度[8].

为了降低Sigmoid函数在ARM Cortex-M平台上的运算复杂度，本文提出一种新的Sigmoid激活函数优化方法—分段极限近似法.首先根据Sigmoid函数在中间变化快、两端变化缓慢的特点，将其分为常数区和非线性拟合区；其次依据第2个重要极限公式将Sigmoid函数中的指数计算转换为log2n次乘法计算，简化e指数计算进而降低Sigmoid函数的运算复杂度.实验表明，这种优化方法相比标准C的math库exp函数实现Sigmoid函数的方法在运算速度上可以提升23.67倍；准确率上，在平均绝对误差小于0.001的情况下该方法产生的拟合误差不会造成神经网络判别准确率的下降.

2 原理与方法

2.1 Sigmoid函数的区域划分

Sigmoid函数是一种广泛应用于神经网络的激活函数[9]，其计算公式如式(1)所示，其值域为(0，1).

(1)

Sigmoid函数及其一阶导函数、二阶导函数如图1所示.Sigmoid函数的一阶导数反映其变化率，变化率小表明值变化速度缓慢，变化率较小的区间可用常数来拟合.将Sigmoid函数分为两个区间：常数区和非线性拟合区.这两个区间的分界点取决于常数区与“1”之间的最大允许误差Δ，如式(2)所示.本文设置最大允许误差为0.003，代入式(2)计算，可得常数区与非线性拟合区的分界点x为6.由于Sigmoid函数的对称性，负半轴的分界点x为-6，常数区定为(-∞，-6)和(6，+∞)，非线性拟合区为[-6，6].(-∞，-6)用常数“0”拟合，(6，+∞)用常数“1”拟合，[-6，6]用非线性函数拟合.

图1 Sigmoid函数及其一阶、二阶导数

(2)

Sigmoid函数的一阶导数和二阶导数的计算公式如式(3)、式(4)所示.

(3)

(4)

Sigmoid函数的二阶导数在(-∞，0)内恒大于零，在(0，+∞)内恒小于零.因此Sigmoid函数的变化率函数在(-∞，0)单调递增，在(0，+∞)单调递减.

由Sigmoid函数的一阶导数即式(3)计算可得：常数区与非线性拟合区的分界点变化率为0.0025.根据Sigmoid函数变化率在区间(0，+∞)单调递减的特性可知，常数区(6，+∞)内Sigmoid函数的变化率均小于0.0025，根据对称性可知在(-∞，-6)区间函数的变化率均小于0.0025，即在区间(-∞，-6)和(6，+∞)内使用常数拟合不会产生较大误差.

2.2 非线性拟合

Sigmoid函数主体为e指数运算，e指数运算为超越函数，影响了Sigmoid函数在非线性区间的计算效率.在计算机中，标准C math库的e指数的实现方法是泰勒级数展开法，这种方法复杂度高.本文在设定误差内提出一种运算量小，资源消耗低的非线性函数，以实现指数函数的近似计算.

第2个重要极限公式如式(5)所示：

(5)

命名n为极限参数，由式(5)可以推出：

(6)

(7)

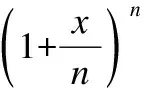
图2 极限近似法满二叉树计算

t=log2n+1

(8)

可得t-1=log2n，因而，利用公式(6)，e指数计算可以转换成log2n次乘法计算，降低其在处理器中的计算时间复杂度.

利用式(7)对Sigmoid函数进行非线性拟合，本文命名这种拟合方法为极限近似法.

极限参数n的选取条件取决于选定区间内e指数计算所允许的均方误差.对于给定区间[x1，x2]，设均方误差为ξ，则：

由泰勒级数展开公式：

(9)

(10)

区间[x1，x2]均方误差为：

(11)

求解得：

(12)

(13)

本文得出e的拟合方程式(6)的极限参数n的求解公式(13)，其给定区间为[x1，x2]，设定的e指数均方误差为ξ.

前述均方误差计算区间为[-6，6]，即x1=-6，x2=6时，求解极限参数n为式(14).

(14)

2.3 e指数拟合精度与速度分析

e指数泰勒级数展开公式如式(15)所示.

(15)

由上式可知，当展开次数为n(n≥2)时，计算e指数需要用到n次加法和2(n-1)次乘法，运算复杂度高.

比较本文的极限近似法与泰勒级数展开法在相同乘法次数下对e指数的拟合精度，计算其均方误差，见式(16).

(16)

γ(x)=f(x)-ex

(17)

[x1，x2]为计算均方误差的区间，由公式(2)计算可得非线性拟合区为[-6，6]，因此仅在此区间计算均方误差，即x1=-6，x2=6.f(x)为拟合函数.

表1为在相同乘法次数下，极限近似法和泰勒级数展开法对e指数拟合的均方误差.图3为极限近似法和泰勒级数展开法对e指数拟合的均方误差取对数(e为底)形式下的曲线图.可知，在相同乘法次数下泰勒级数展开法的均方误差远大于极限近似法的均方误差.两种方法的均方误差均随着乘法次数的增加而减小，因此精度与速度是相互对立的关系.因而，在相同计算时间情况下极限近似法相较泰勒级数展开法可以取得更高的精度.

表1 相同乘法次数下两种方法e指数的均方误差(x∈[-6，6])

图3 e指数均方误差曲线图

2.4 Sigmoid拟合性能分析

本文利用MATLAB工具分析Sigmoid函数的拟合性能，在非线性拟合区间内计算Sigmoid函数的平均绝对误差.非线性拟合区间以 0.001为间隔取数，Sigmoid函数的平均绝对误差计算结果如表2所示.

表2 Sigmoid函数平均绝对误差(x∈[-6，6])

由表2可知，随着极限参数n的增大，Sigmoid函数的平均绝对误差越小，拟合精度越高，相应计算时间越长.Sigmoid函数平均绝对误差的对数形式(e为底)与e指数均方误差的对数形式的关系如图4所示.

图4 Sigmoid平均绝对误差与e指数均方误差关系图

由图4可知：二者具有近似线性的关系，线性回归拟合公式如式(18)所示.

y=0.5078x-9.1696

(18)

y为Sigmoid函数平均绝对误差的对数形式，x为e指数均方误差的对数形式.假定Sigmoid平均绝对误差为λ，由式(14)及式(18)可得极限参数n与λ的关系式：

(19)

3 实验与结果

为了验证Sigmoid函数分段极限近似法对嵌入式计算平台神经网络计算效率的影响，本文以ARM Cortex-M实验平台为验证系统进行了实验.

3.1 实验条件

BP神经网络通过前向传播、误差反向传播和权重更新这3个过程进行训练[10].训练过程运算量大，因此神经网络的训练部分在处理能力强的PC端进行，训练结束后的权重参数存于文件，在ARM Cortex-M平台上导入权重参数进行测试.

实验主要分为PC端数据集训练以及ARM Cortex-M平台数据集测试这两个部分.PC端实验环境为Anaconda3，编程语言采用Python3.7.实验网络为全连接层神经网络，其结构如图5所示.神经网络框架编程采用TensorFlow深度神经网络开源软件库.ARM Cortex-M平台上选用STM32F407ZGT6芯片进行实验，其工作频率为168MHz.利用广州市星翼电子科技有限公司生产的探索者STM32F407开发板，ARM开发环境采用MDK5软件，版本号为5.25，并使用C语言进行编程.图6为实验验证框图.

图5 神经网络示意图

图6 实验验证框图

3.2 验证数据库

验证数据库采用UCI数据库，该数据库由加州大学欧文分校(University of CaliforniaIrvine)提出，用于机器学习标准测试，是目前学术界广泛使用的机器学习数据库[11].

本文从UCI数据库中选择了5个用于分类任务的数据集进行训练和测试.表3为从UCI数据库中选择数据集的基本信息.

表3 实验数据集描述

神经网络模型训练的测试集与训练集之比为3∶7，实验中ARM Cortex-M平台上运行神经网络的数据集为测试集数据.

3.3 实验方法

首先从UCI数据库中选取用于分类任务的数据集完成PC端BP神经网络的设计、训练、验证，训练后的权重参数保存至文件.然后，在ARM Cortex-M平台上复原神经网络并导入已训练得到的权重参数运行神经网络，利用不同Sigmoid实现方法比较神经网络运行速度.最后，对ARM Cortex-M实验系统和PC实验系统神经网络的测试准确率进行比较.表4为各数据集神经网络模型的结构和Sigmoid函数的使用情况.

表4 神经网络结构及Sigmoid函数的使用情况

本文提出的分段极限近似法实质为一种分段拟合法，文献[8]也提及了一种利用多项式进行Sigmoid函数分段拟合优化的方法.本文对比分段极限近似法及文献[8]分段拟合法对标准C的math库exp函数实现Sigmoid函数的方法运算速度提升情况，验证计算平台为ARM Cortex-M平台.

文献[8]采用的分段拟合法将Sigmoid函数的绝对误差控制在0.001以内，因此本文极限近似法设定的平均绝对误差也为0.001，代入公式(19)计算得：n=274.85，取2的整数次幂得：n=512.

3.4 运算时间实验分析

为了验证分段极限近似法对Sigmoid函数在ARM Cortex-M平台上对神经网络运算速度的影响，在ARM Cortex-M平台上复原PC端的神经网络，利用UCI数据库中的数据集进行测试.表5为本文ARM Cortex-M平台上的输出层平均绝对误差，输出层平均绝对误差指嵌入式平台上使用本文的极限近似法实现Sigmoid函数的神经网络最后一层输出的结果与计算机端利用math函数库实现Sigmoid函数的神经网络最后一层输出的结果之差的平均值.表6为不同数据集使用不同Sigmoid函数实现方法的神经网络运算时间比较.时间的测量通过开启ARM的定时器测定.

表5 数据集输出层平均绝对误差

表6 神经网络运算时间比较

实验数据表明，在表5所示的各数据集输出层平均绝对误差的范围内，分段极限近似法及文献[8]分段拟合法对标准C的math库exp函数实现Sigmoid函数的方法在速度上可分别平均提升24.67倍和4.94倍.在相同误差数量级下分段极限近似法对速度提升效果更加显著.

3.5 准确率实验分析

由于拟合误差的存在，每一层神经元的值都会发生变化(增加或减少)，从而影响下一层神经元的值；在输出层，当两个神经元的值很接近时，整个网络中积累的误差会导致网络识别的结果发生变化[12].为了验证分段极限近似法对准确率的影响，本文在ARM Cortex-M平台上复原与PC端一致的神经网络，并导入已训练后的权重参数，然后利用PC端的测试集数据对ARM Cortex-M平台上的神经网络进行测试，分段极限近似法的Sigmoid函数平均绝对误差设置为0.001.表7为PC和ARM Cortex-M平台的神经网络判别准确率的比较.

表7 神经网络准确率比较

实验结果表明，ARM Cortex-M平台上神经网络判别准确率与PC端的准确率一致，说明在平均绝对误差小于0.001的情况下分段极限近似法对Sigmoid函数产生的拟合误差不会造成神经网络判别准确率的下降.

综合神经网络运算速度和识别准确率的实验数据，可以得出在ARM Cortex-M平台上，通过降低Sigmoid激活函数运算复杂度，分段极限近似法在确保判别准确率的前提下提升了神经网络的运算速度，同时具备了低计算时间复杂度和高精度的优点.

4 结 论

本文提出一种新的Sigmoid函数优化方法——分段极限近似法，在资源受限的嵌入式平台上能够不影响判别准确率的前提下有效降低神经网络计算时间复杂度.该方法通过选择合适的极限参数值，同时满足ARM Cortex-M平台上的精度和速度的需求.实验表明Sigmoid函数的实现，该方法相较标准C的math库exp函数可以提升23.67倍的速度，且在平均绝对误差小于0.001的情况下对Sigmoid函数产生的拟合误差不会造成神经网络判别准确率的下降.该方法为嵌入式平台上神经网络的低复杂度、高精度运行提供一种优化方法.