一种通过强化学习的四旋翼姿态控制算法
2021-02-28贾振宇刘子龙
贾振宇,刘子龙
(上海理工大学 光电信息与计算机工程学院,上海 200093)
1 引 言
四旋翼在二十世纪初进入人们视野,且有数篇文章提取具体的建模方法和控制方法.作为一个典型的多输入多输出的非线性系统,具有强耦合,欠驱动等等一系列控制难点[1,2].针对四旋翼无人机控制系统的特点,研究人员提出了众多控制算法来优化无人机的姿态控制.尽管四旋翼这些年中取得了重大进展,但仍然面临诸多难点.首先,鉴于飞机的实时控制需要实时地采集和计算数据,所以就需要高度的时间敏感性.其次,飞机在飞行过程中应该能够适应各种复杂和恶劣的环境下保持姿态的稳定.考虑到这些因素,飞行控制仍然是一个机器热门的研究问题.
目前的主流控制算法还是以PID为主[3,4],然而其抗干扰依托于积分项,当积分误差实时变化时,其抗干扰能力会很差,更重要的是PID的增益需要根据环境变化反复实现进行选择,难以满足其动态性能.因此,诸多研究者为了更好的克服这些问题,提出了许多高级控制策略来保证姿态的稳定:通过模型预测控制[5],鲁棒控制[6]和滑模控制[7]等,但这些方法却都又存在一个共同的问题,控制策略与当前模型的确定性关系很大.如果模型不够准确即忽视外部干扰,那么这些控制方案就无法实现理想的控制效果.但如果模型为了准确性而过于复杂,这会使控制率也变得异常复杂.
在过去数十年,人工智能技术的飞速发展也切实影响到了传统控制领域.以机器学习构建控制系统成为了一个热门话题[8],因为就算是不确定的非线性模型,神经网络也能有着相当出色的表现[9].但是一般通过监督学习方法实现行为克隆往往效果会很差,原因是网络收集数据和正确数据的不匹配的原因造成的[10].为了克服监督学习方法的不足,强化学习提了出来.在2005年,首次通过强化学习来实现四旋翼的模型控制[11],采用局部加权的线性回归将四旋翼建模构成一个马尔可夫链,学习的控制策略与积分滑模控制有着接近的性能.近些年,大量深度学习算法施加在强化学习构成新的深度强化学习,这些算法都有着更加卓越的性能.诸如确定性策略梯度DPG[12],深度确定性策略梯度DDPG[13],信任域策略优化TRPO[14]和近端策略优化PPO[15]都在连续状态行动空间中展示出卓越的控制性能[16].最近通过自然梯度下降方法优化确定性策略,神经网络将给定状态映射到飞机可执行动作向量集,从而成功学习了控制策略实现飞机姿态的控制的同时,在相对恶劣的条件下都有着出色的性能[17].但是,实际环境与模拟环境之间存在许多差异.从模拟环境中学到的飞机模型直接应用于实际环境会引起很多问题.例如准确性和稳定性下降,此外飞行任务的变化和环境的变化会造成飞行策略的不稳定.
故本文在上述的基础上提出通过模型改进强化学习算法(MB-PPO).以近端策略优化算法为基础并结合模型提出改进,修改了原先近端策略优化算法的价值判断和策略优化算法.经过验证,可以发现改进后的算法在四旋翼姿态稳定中更具泛用性且更快收敛.
2 背 景
本文使用的强化学习方法是采取确定性策略和自然梯度下降[18]的一种结合.确定性策略普遍相较于随即策略存在一些缺点.确定性策略不像随机性策略,并不能很好的探索所有状态空间,而且从一般角度出发,随机策略一般也能比确定性策略在解决问题上面有着更好的表现.虽然没有确切的证明,但猜测是随机性策略比起确定性策略不那么容易陷入局部最小点.
本文依旧采用确定性策略是因为相较于随机性策略还是有如下几点主要优势:首先比起随机性策略有着更低的方差,这样可以使学习更较稳定.其次就是可以将策略梯度更加简洁,便于计算,对于随机性策略这种非连续动作空间算法来说,列举所有的动作空间过于困难.
一个确定性环境马尔可夫决策过程可以通过一些可能的输出A和状态S.因为真实四旋翼的动力学模型是可以通过微分方程表示f:S×A→S,对应的奖励函数为r:S×A→.于是马尔可夫链如式(1)所示:
(s1:T+1,a1:T,r1:T)
(1)
本文的目标就是寻找到一个最优的确定性策略πθ,其中θ表示策略的参数,在随机性策略中的目标要最大化策略生成可能轨迹下轨迹奖励的期望:
(2)
其中dπθ(s)表示访问频率函数,Vπθ(s)表示某个状态之后产生所有可能的轨迹奖励的期望,也被称为价值函数:
dπθ(s)=P(s0=s)+γP(s1=s)+…
此处采用的是确定型策略,于是自然将得出如下两个结论:
st+1=fπ(st)=f(st,at)|at=π(st)
(3)
其中Qπθ被称为动作价值函数.这个函数的输出可以理解成特定策略下特定状态做出特定动作的价值函数.
本文对策略πθ改进成确定性策略的深度神经网络结构.确定性策略梯度下降可以写成:
本文采取的基准是Vπθ(s),即价值函数,则策略梯度下降可以进一步写成:
(4)
其中Aπθ(s,πθ(s))=Qπθ(s,πθ(s))-Vπθ(s)也被称为优势函数.这个函数的输出可以理解成特定策略下特定状态做出特定动作本身的奖励.
一般在策略梯度算法中有人次策略梯度能够提升的算法极限,构成(5)式中上半段无条件优化问题,但因为两个策略之间比值差距过大过小将会造成期望本身要么趋向于无穷要么趋向于0,不利于计算,于是为了解决这个问题,自然梯度下降提出每次更新两个分布之间的差距要趋向于1,于是引入KL散度,构成约束优化问题:
maxmizeθLπθ(πθ′)
s.t.DKL(πθ‖πθ′)≤
(5)
其中Lπθ(πθ′)表示参数变化后的策略奖励差距:
随之可以将公式(5)中的约束项转换成规划中的惩罚项,并通过对其中规划主体线性近似和对惩罚项进行二次近似,进一步写成如下形式:
(6)
其中g是η(πθ)的一阶近似,F是KL散度作为惩罚项的二阶近似,且为费舍尔信息阵:
F=πθ[∇θlogπθ(s)∇θlogπθ(s)T]
最后求解得出的自然策略梯度如下
(7)
自然梯度下降的问题在于费舍尔矩阵难以计算,对此有两个经典改进:TRPO和PPO.TRPO提出F这个费舍尔矩阵求逆可以通过共轭梯度法简化了运算.
但就算如此整个计算式也相当复杂,故引入新的自然梯度做法,即PPO.PPO并没有解决费舍尔矩阵,而是另辟蹊径,直接提出单次梯度更新不要让分布差距过大,如果差距过大,直接裁剪掉,设置单次更新距离极限.于是策略差距演化成如下形式,这很大程度简化了运算和编程的复杂度.
3 具体方法
3.1 网络结构
训练网络正如上方所述,通过无模型强化学习和基于模型进行结合构成新的网络结构构成的新算法MB-PPO.
如图1所示,MB-PPO的输入分成两个部分,一部分是通过完全基于模型的反步法得出的运动,另一部分是一般神经网络.
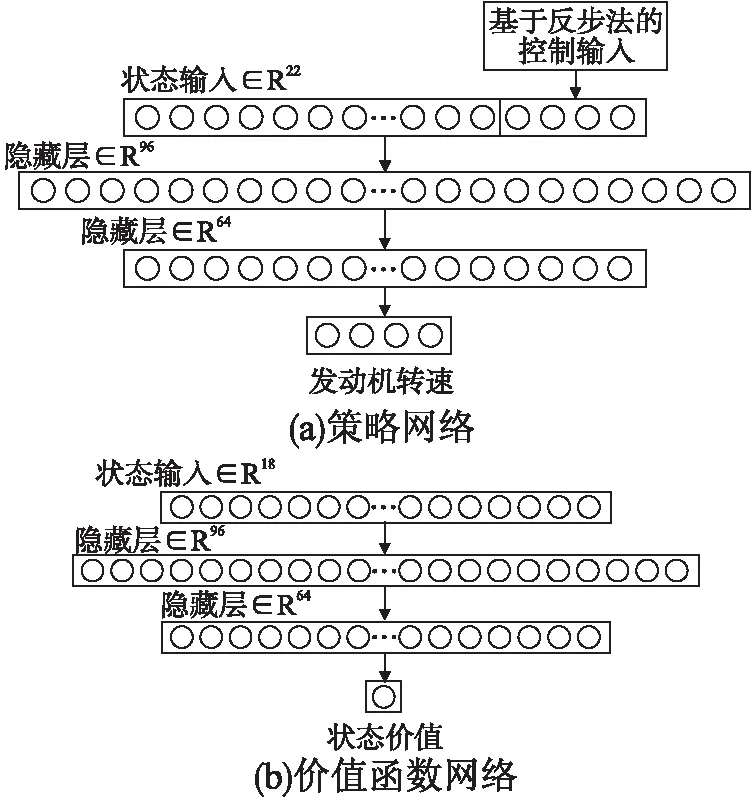
图1 网络结构图
两边网络都是以四旋翼的状态作为初始输入.使用的状态输入为表示旋转姿态的旋转矩阵的9个元素,再额外加上位置,线速度和角速度.价值网络和策略网络的区别在于策略网络额外通过反步法[19]计算得出的动作额外添加在状态输入,即决策网络从两边同时获取输入:无模型的18维输入和另外4维的动作输入,价值网络只有当前状态的18维作为输入.
PPO能只通过相对粗糙的神经网络得出哪怕在恶劣的条件下都能良好控制的控制效果,但这是通过大量试错下产生的.而反步法在给出确定的模型时虽然也能有良好的控制效果,但是这需要极其准确的模型而得出极其复杂的控制律,所以将两者结合.在给反步法一个合理的模型并给出控制并将这份控制作为额外知识输入到强化学习网络进一步减少强化学习试错的过程提升学习效率.
具体网络结构是价值网络输入18和策略网络输入22维的状态向量和对应的1维价值输出和4维的动作输出,采用具体的网络结构是2层分别为96个节点和64个节点.
3.2 基于仿真模型探索方法
确定性策略下如果环境是唯一确定的,那么其价值函数是准确的,如(3)式所示.但采样数据随着传感器精度变化而变换,导致采样不稳定,造成奖励存在干扰.
所以强化学习需求大量真实数据来拟合,需要收集大量数据才能对真实状态价值做出准确的判断,但是这对机器人来说进行大量的数据采样是极其困难的.其次更糟糕的在于仿真环境中机器人环境是唯一确定的,造成了其价值唯一确定且与真实世界不符,难以在真实世界复现.
故此处为了在仿真中能采样到合适的数据,使用的方法和一种称为vane[17]的方法类似.
通过对仿真中构成的唯一确定的初始轨迹中的状态,人工对其叠加协方差Σ的高斯噪声构成的状态偏移,在这偏移的轨迹下构成新的分支轨迹.具体形式结构请参考图2,图2是对一个状态下扩展出两个新的状态构成额外的2条分支轨迹.这种方法可以有效解决确定性策略在仿真环境中无法很好探索状态空间的问题.
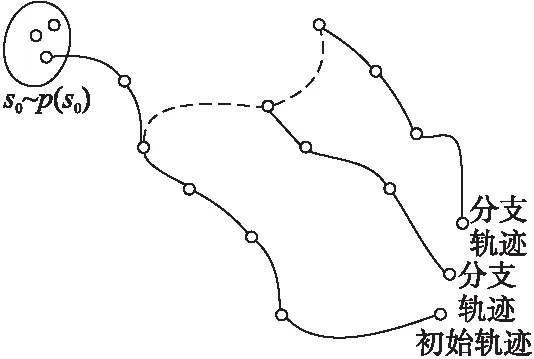
图2 探索策略
3.3 价值函数标签
所有价值函数训练用的价值函数都通过蒙特卡洛方法将轨迹的奖励叠加.其中当仿真轨迹生成和真实四旋翼采样一致的状态时,其价值函数的计算略有不同:
(8)
前半部分是借于仿真模型方法生成的N条轨迹的状态平均价值,N的具体数量由仿真产生相同状态的数目决定;后半段是采样的真实状态价值,通过上述轨迹的均值产出的状态价值.
所有训练集和对应标签都通过上述方法所述获取,每获取一条真实轨迹和大量仿真轨迹后使用监督学习方法优化价值函数.因为数据本身误差存在可能比较大,本文没有选择平方损失函数,而是Huber损失函数.当误差小于0.001时,视系统该轮价值函数优化完成:
(9)
4 训练过程
本文通过Crazyflie(1)https://www.bitcraze.io/生成真实的轨迹,gazebo作为仿真模型生成额外的轨迹.之所以通过gazebo进行建模,是因为物理引擎强大且便于实现,另两者都可以直接通过ROS实现控制,大幅度降低了代码难度.
4.1 仿真模型建立
此处建立的是一个没有外部干扰的简单模型,通过牛顿欧拉方程构成:
JTT=Ma+h
(10)
其中J表示转子中心的雅可比矩阵,T是推力,M是惯性矩阵,a是广义加速度,h是重力和科氏力等.具体设置的参数可参考表1.
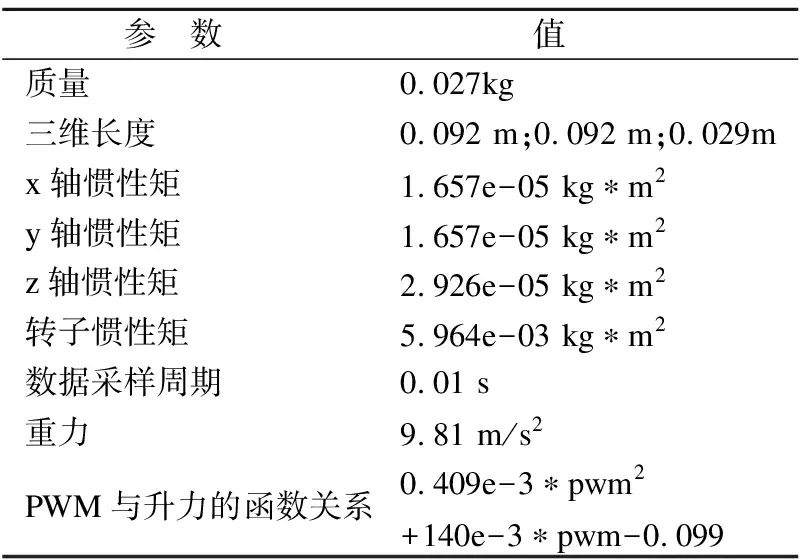
表1 仿真参数
4.2 反步法控制模型建立
此处是将集体角速度假设等于空间角速度构成的非线性动力学模型,具体形式如下:
(11)
此处是通过牛顿欧拉动力学展开的四旋翼控制模型.通过构造状态向量,分成两个子系统形成内外环控制,随后通过反步法[19]得出如下具体的四旋翼控制输入:
此外神经网络训练形式是完全的单对单模型,故此处还需要进一步转换成发动机转速.
4.3 网络训练
在训练过程中,算法的奖励函数,定义如下:
rt=cp‖pt‖+cv‖vt‖+cω‖ωt‖
(12)
其中前3项表示成本系数,后3项分别是t时刻四旋翼速度,角速度与原点的距离的二范数.
综上所述,将四旋翼训练目标设定成走到原点上.训练的输入是当前姿态作为强化学习网络的输入到网络中,并策略网络产生控制,价值网络产生对应状态价值.具体算法流程可参照算法1,在上述飞行器和构造的模型中进行学习.具体网络参数可参考表2.
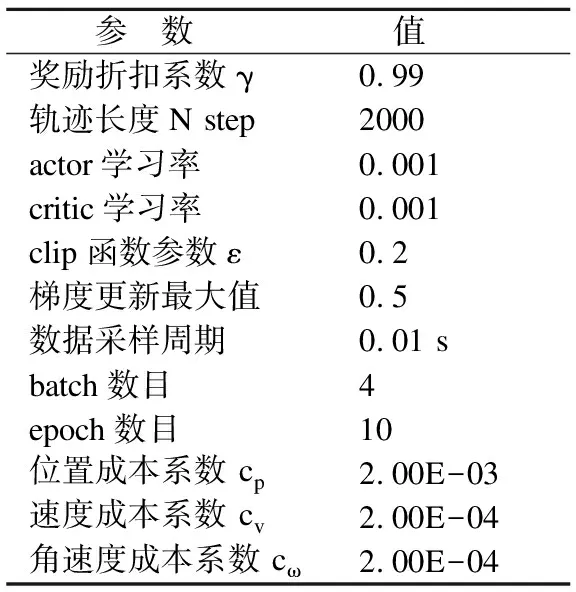
表2 算法参数
算法1:MB-PPO
1.构建仿真模型
2.初始化价值网络和策略网络
3.设置网络相关参数
4.While(一直到收敛为止)
{
5. 获取初始状态Si
6. 将Si输入仿真模型采取仿真轨迹
7. 将Si作为初始状态获取飞机轨迹
8. 通过式(11)获取所有状态的奖励ct
9. 通过式(8)获取所有状态的价值标签vi
10. 通过梯度下降更新价值网络参数φ
11. 进一步更新策略网络参数θ
}
4.4 训练结果
从图3可以看出MB-PPO仅200次迭代左右四旋翼可以趋于稳定,比起传统强化学习迭代更新速度提升更大.图4是飞机算法开始迭代时抓拍的图像.
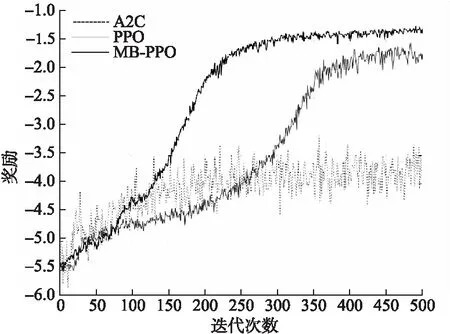
图3 不同结构网络学习曲线

图4 四旋翼训练图像
虽然飞行器趋于稳定,但通过学习曲线发现实际算法始终存在一定的稳态误差,这一部分继续尝试训练也并没有有效收敛.然而稳态误差相对较小,因此有提出直接通过常数偏移[17]或者通过引入状态积分补偿[20]来解决.
5 实验和实验结果
5.1 实验设置
此处为了进一步验证MB-PPO的优势,将上述算法在上述标准情况下迭代训练1000次后,修改任务目标,即系统的奖励或者惩罚函数形式变化如式(13)所示:
rt=cp‖pt-pdes‖+cv‖vt‖+cω‖ωt‖+co‖ot‖
(13)
co表示成本系数,ot额外表示机头的朝向,此处所处位置必须与地面系齐平,并且稳定位置于pdes不在原点.
5.2 实验结论
图5可以明显看出当要求变化后,传统PPO算法为了摆脱算法训练回到原点的影响,在接近1000次迭代过程后才与MB-PPO初始迭代时齐平.
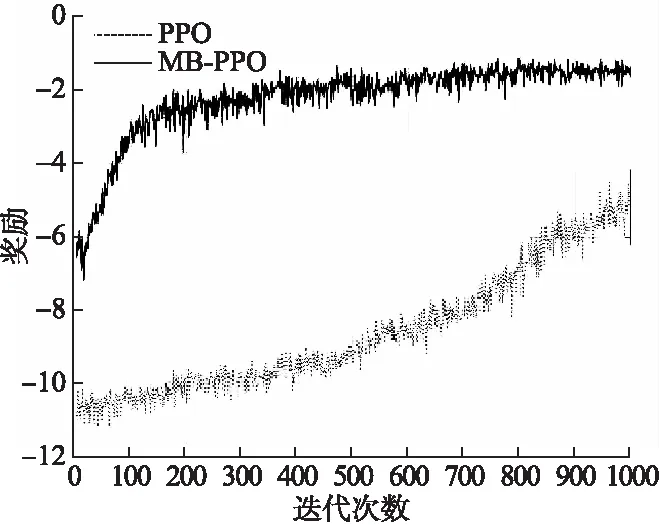
图5 任务目标变化的学习曲线
图6(a)更加明显地给出了PPO算法在任务要求发生变化时的姿态角度变化,可以明显看出传统PPO算法在10s左右横滚角和俯仰角趋向于0,使四旋翼姿态接近稳定,但是由于目标的改变,算法为了继续收敛只能继续不断探索状态空间,然而算法已经迭代到了一个相对较高的价值位置,很难跳出先收敛到训练目标点这一步.
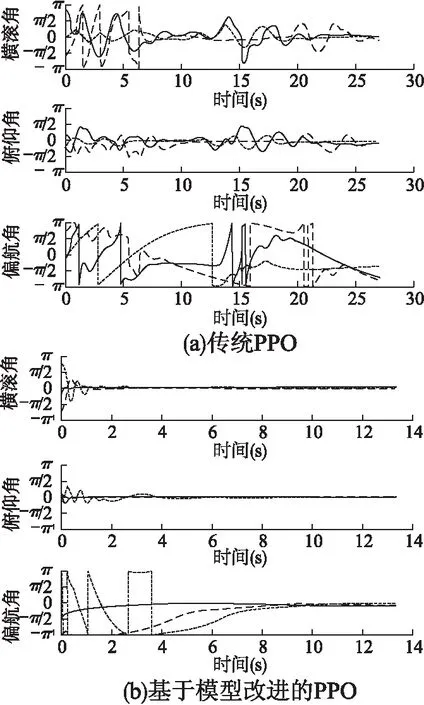
图6 目标变化后的角度收敛曲线
6 总 结
本文针对四旋翼无人机的非线性,强耦合,欠驱动等控制难点提供了一个新的基于模型的强化学习网络.在训练中通过对控制模型的依赖.训练好的策略模型显示着出色的性能,同时计算复杂度很低.相比普通的强化学习能够更快收敛,且在不同任务切换后,依旧快速收敛.实验也证明了这个算法具有较快的响应速度,良好的泛用性.
