可变节流高度气浮支承结构设计及静态性能分析*

胡江山 秦 丽 于普良 李 双

(1.武汉科技大学冶金装备及控制教育部重点实验室 湖北武汉 430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室 湖北武汉 430081;3.武汉科技大学精密制造研究院 湖北武汉 430081)

气浮支承具有无摩擦、无需润滑和工作精度高等优点，已经成为超精密机床运动系统的主要支承方式。但气体的可压缩性导致气浮支承的刚度、承载力等静态性能较差，探究提高气浮支承性能的方法已经成为超精密制造领域重点研究方向[1-6]。

针对这一问题，许多学者提出通过改变气浮支承节流方式和表面微织构或施加主动控制等方式来提高气浮支承静态特性，并且已经得到了一些研究成果。文献[7-10]探究了不同表面节流结构、小孔进气方式等结构参数对气浮支承静态性能的影响，发现节流方式和进气方式的优化对气浮支承静态性能的提高效果有限。文献[11-15]提出对气浮支承进行主动控制来提高支承系统的静、动态性能。目前主动控制技术已经成为提升气浮支承静态性能的重点发展方向。研究表明：真空预加载主动控制技术在提高气浮支承动刚度的同时会降低系统承载能力的问题，限制了其运用；电磁主动控制技术工作精度高，但也存在驱动单元的体积过大和电磁干扰过大的缺点；压电主动控制技术控制精度高且控制方法简单，已经成为主动控制方法的主流。谢建、朱定玉[16-17]通过压电主动控制气浮支承气膜形状提高了气浮支承静态性能,但该系统的控制方法极为复杂且控制精度较低。PIPELEERS、MIZUMOTO等[18-19]通过压电主动控制节流面积提高了气浮支承静态性能，但仍需要解决由密封圈导致的摩擦问题。

综上，目前鲜有关于节流高度变化对气浮支承性能影响规律的研究报道。本文作者设计了一种可变节流高度气浮支承，分析了节流口直径、均压腔深度、供气压力和节流高度对气浮支承静态性能的影响规律。

1 可变节流高度气浮支承结构模型及控制方程

1.1 可变节流高度气浮支承结构模型

可变节流高度的气浮支承结构示意图如图1所示。气浮支承本体主要由上端盖10a、柔性机构8和下支承10b构成，气浮支承的节流高度变化示意图如图2所示。改变施加在柔性机构上作用力F可以改变气浮支承的节流高度，节流口高度的变化直接影响气浮支承的气体流量，进而达到调节气浮支承静态特性的目的。气浮支承的结构参数如表1所示。

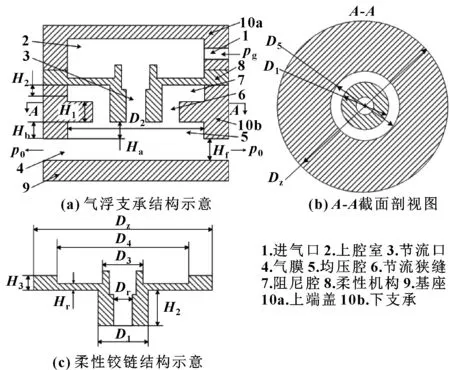
图1 可变节流高度气浮支承结构示意

图2 气浮支承的节流高度变化示意

表1 气浮支承结构参数

1.2 气体润滑控制方程

连续性方程：根据质量守恒定律，气浮支承空间损失的质量等于流出的质量，定义流出质量为负，得到气浮支承连续性方程[20]为

(1)

式中：ρ是气体密度；t是时间；u、v、w分别为速度矢量V在x、y、z3个方向的分量。

运动方程：根据动量守恒定律，流体运动方程[20]为

(2)

式中：p为气浮支承气域压力。

纳维-斯托克斯方程：假设气体的流动为层流，忽略其他方向速率变化对切应力的影响，得到气浮支承流域的纳维-斯托克斯方程[20]为

(3)

式中：λ=μ/ρ，μ为动力黏性系数；Fx、Fy、Fz为单位质量流体的体积力F在坐标轴方向的相应分量。

在气浮支承达到稳态后，气浮支承的气膜假设是稳定不变的，对气浮支承气域的压力进行面积分可以得到气浮支承静承载力为

Fn=∬(p-p0)dxdy

(4)

式中：p0为大气压力。

气浮支承静刚度为

(5)

式中：Hf为气浮支承气膜厚度。

1.3 可变节流高度气浮支承CFD模型

气浮支承流域CFD模型的仿真计算设定为：假设气浮支承的流体为不可压缩黏性气体，选用层流计算模型。气体流域分为4个区域：节流口流域、均压腔流域、阻尼腔流域和气膜流域。由于气浮支承的气域具有对称性，在保证仿真模拟准确性的前提下，只建立了气体流域模型的 1/4进行仿真计算。图3所示为可变节流高度气浮支承的气体流域模型。气体流域的两边界为对称边界(symmetry)；节流口的上表面为压力进口(pressure-inlet)，供气压力为pg；气体流域的外边界为气体溢散处，设置压力出口(pressure-outlet)，大气压力p0=0.1 MPa；所有壁面(wall)均为无滑移壁面。使用六面体网格对气体流域进行网格划分，并在节流口流域和均压腔流域进行局部网格加密，气浮支承气域的CFD模型如图4所示。

图3 可变节流高度气浮支承气体流域示意

图4 可变节流高度气浮支承CFD模型

2 仿真分析方法适用性验证

采用文献[21]中气浮支承模型，并利用层流计算模型分析该气浮支承的静态性能，将仿真分析结果与文中采用湍流模型得出的数据和试验数据进行对比分析，以此来验证用于气浮支承静态性能分析的层流计算模型的适用性。文献[21]中的气浮支承结构示意图如图5(a)所示，其中：气浮支承半径ra=25 mm，节流口直径D0=0.85 mm，气膜厚度Hf=60 μm。仿真分析模型为湍流模型，进气口压力pg=0.6 MPa，出口压力p0=0.1 MPa。

图5(b)示出了分别采用层流计算模型、湍流计算模型和试验得到的气浮支承径向压力数值，可以发现通过层流计算模型、湍流计算模型和试验得出的气浮支承静态特性具有一致性，验证了层流计算模型对气浮支承进行静态特性计算的适用性和正确性。

图5 气浮支承结构示意和径向压力对比

3 仿真结果及分析

在气膜厚度Hf=10 μm，均压腔高度Hb=20 μm，进气压力pg=0.6 MPa，其他几何参数不变的条件下，仿真分别得到的气浮支承的节流高度Ha分别为-2、0、20、30 μm时主动气浮支承的压力分布如图6所示。沿气浮支承的径向，与Y轴的夹角β为45°，深度为5 μm处取一条压力分布径向直线，不同节流高度气浮支承径向压力分布曲线如图7所示。通过图6和图7可以发现：节流高度为20 μm和30 μm的气浮支承的压力分布相近，且明显高于节流高度为-2 μm 和0时的气浮支承。综上，气浮支承节流高度的增大能显著地提高气浮支承气域的压力分布和承载能力，且当节流高度达到20 μm左右时，气浮支承承载能力达到峰值。通过调节气浮支承的节流高度能够显著地改变气浮支承承载能力等静态特性。

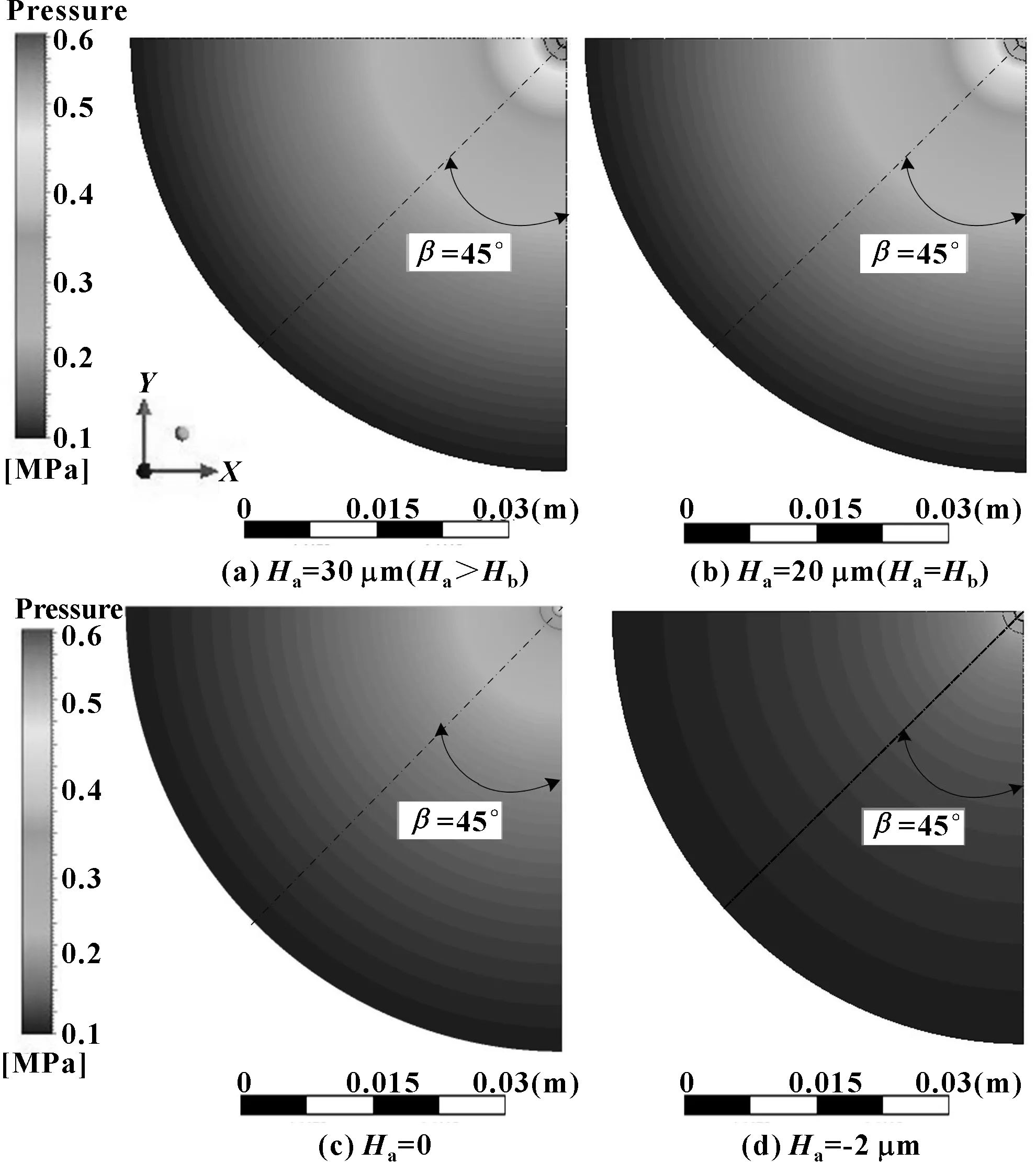
图6 不同节流高度气浮支承压力云图

图7 不同节流高度气浮支承径向压力分布曲线

3.1 节流口直径对气浮支承静态性能的影响

当Dr分别为100、150、200、250、300 μm，pg=0.6 MPa，Ha=Hb=20 μm，其他结构参数不变时，探究气浮支承节流口直径对气浮支承静态性能的影响，结果如图8所示。

图8(a)所示为气浮支承承载力随节流口直径的变化关系曲线，可见节流口直径的增大能显著地提高气浮支承的承载能力。图8(b)所示为气浮支承刚度随节流口直径的变化关系曲线，可见气浮支承的刚度随气浮支承节流口直径的增大而减小。图8(c)所示为气浮支承体积流量随节流高度的变化关系曲线，可见气浮支承的体积流量随节流高度的增大而增大。

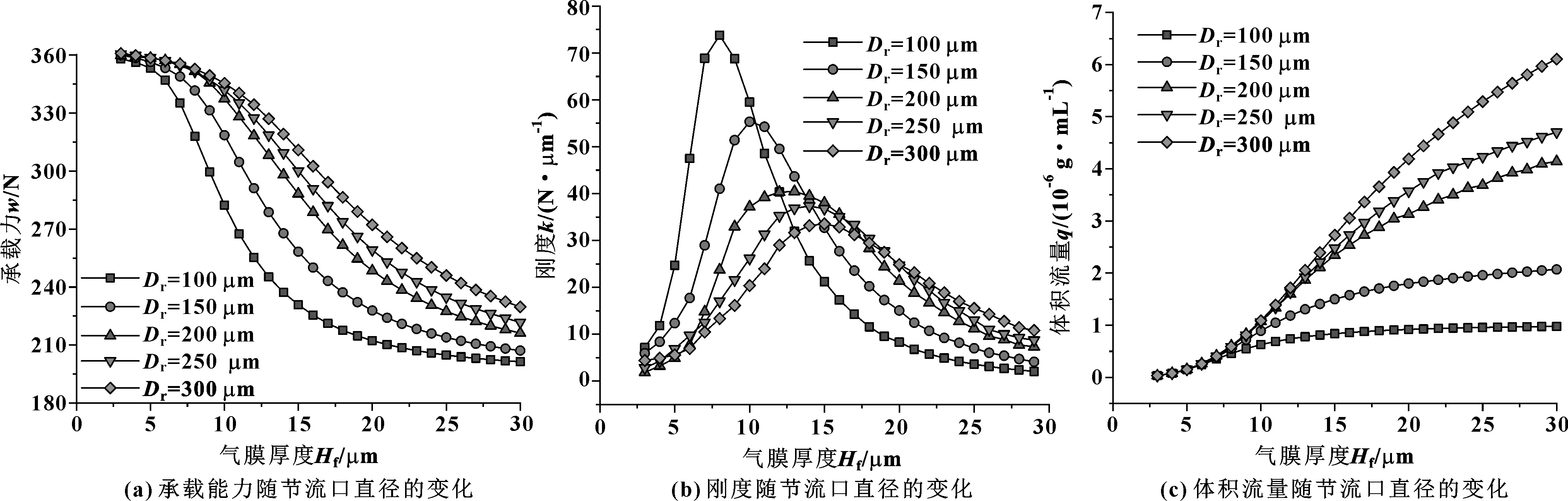
图8 节流口直径对气浮支承静态性能的影响

综上所述，随着进气口直径的增大，气浮支承的承载力逐渐增大，刚度逐渐减小，气体体积流量增大。当进气口直径达到200 μm后，承载力增大的幅度降低；当进气口直径继续增大到300 μm时，对比进气口直径为200 μm可以发现，气浮支承承载能力的提升已较小，而刚度降低，气体流量显著增大。所以气浮支承的进气口直径取200 μm左右时，气浮支承的静态性能较好。

3.2 均压腔深度对气浮支承静态性能的影响

当Ha=Hb=20 μm，pg=0.6 MPa，Dr=200 μm，其他结构参数不变，Hb分别取10、15、20、25、30 μm时，探究均压腔的深度对气浮支承系统静态性能的影响，结果如图9所示。

图9(a)所示为均压腔深度变化对气浮支承承载力的影响规律。随着均压腔深度的增大，气浮支承承载能力逐渐提高，但提升幅度较小。图9(b) 所示为均压腔深度变化对气浮支承刚度的影响规律，可见均压腔深度的变化对气浮支承刚度峰值的影响较弱。图9(c)所示为均压腔深度变化气对浮支承体积流量的影响规律，可见气浮支承的体积流量随气膜的厚度增大而增大。

图9 均压腔高度对气浮支承静态性能的影响规律

综上所述，随着气浮支承均压腔深度的增加，气浮支承的承载能力和刚度的峰值提升较小，而体积流量显著增大。研究表明，气浮支承均压腔深度取20 μm左右时，气浮支承的静态性能较好。

3.3 供气压力对气浮支承静态性能的影响

当Ha=Hb=20 μm，Dr=200 μm，其他结构参数不变，pg分别取0.2、0.3、0.4、0.5、0.6 MPa时，探究供气压力对气浮支承系统静态性能的影响，结果如图10所示。

图10(a)所示为进气口供气压力与气浮支承承载力的关系曲线，可见供气压力的增大会导致气浮支承承载能力的显著提高。图10(b)所示为进气口供气压力与气浮支承刚度的关系曲线，可见供气压力的增大会导致气浮支承刚度显著增强。图10(c)所示为气浮支承供气压力对气浮支承体积流量的影响，可见气浮支承的体积流量随供气压力的增大而增大。

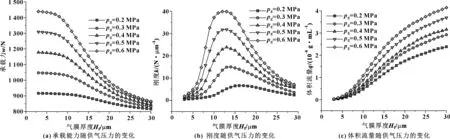
图10 进气压力对气浮支承静态性能的影响规律

综上所述，随着气浮支承供气压力的增大气浮支承的承载能力、刚度和气体流量都明显增大。为提高气浮支承的静态性能，供气压力取0.6 MPa时气浮支承的性能最佳。

3.4 节流口高度对气浮支承静态性能的影响

当pg=0.6 MPa，Hb=20 μm，Dr=200 μm，其他结构参数不变，Ha分别取-2、0、10、20、30 μm时，探究节流高度对气浮支承静态性能的影响，结果如图11所示。

图11 节流高度对气浮支承静态性能的影响

图11(a)所示为气浮支承节流高度与气浮支承承载力的关系曲线，可见节流高度的增大能显著地提高到气浮支承的承载能力，但当节流高度达到20 μm后，节流高度增大气浮支承承载能力不再提高。图11(b)所示为气浮支承刚度与气浮支承节流高度的关系曲线，可见节流高度的增大能提高气浮支承的刚度，但当节流高度达到20 μm左右时，刚度达到峰值；且当节流口高度小于0时，气浮支承具有负刚度。图11(c)所示为气浮支承节流高度与气浮支承体积流量的关系曲线，可见气浮支承的体积流量随节流高度的增大而增大。

综上所述，气浮支承的承载能力和刚度均在节流高度为20 μm左右时达到峰值，所以节流口高度取20 μm左右时，气浮支承的性能最佳。当节流口高度低于气膜厚度时，气浮支承具有负刚度。

4 结论

(1)随着进气口直径的增大，气浮支承的承载力逐渐增大，刚度逐渐减小；当进气口直径达到200 μm后，承载力增大的幅度降低。因此，进气口直径取200 μm左右时，气浮支承的静态性能较好。

(2) 随着气浮支承均压腔深度的增加，气浮支承的承载能力和刚度的峰值提升较小，而体积流量显著增大。研究表明，气浮支承均压腔深度取20 μm左右时，气浮支承静态性能较好。

(3)随着气浮支承供气压力的增大气浮支承的承载能力、刚度和气体流量都明显增大。供气压力取0.6 MPa左右时，气浮支承的静态性能较好。

(4)节流口高度的增大能提高气浮支承的承载能力和刚度。承载能力和刚度均在节流高度为20 μm左右时达到峰值，所以节流口高度取20 μm左右时，气浮支承的静态性能较好。