四维锥形束的CT重建：基于鲁棒主成分分析的运动补偿算法

莫 英，刘 佳，李 仟，马建华，张 华

南方医科大学生物医学工程学院//广东省医学图像处理重点实验室，广东 广州510515

肺癌是当今最常见的恶性肿瘤之一，其发病率和死亡率均不断上升，放射治疗是主要治疗手段之一。目前，临床上多采用3D锥形束CT（3D-CBCT）引导的三维调强、三维适形放射治疗［1-3］。在胸部CBCT容积成像中，呼吸运动会导致重建出的CBCT图像中出现严重的伪影及运动模糊［4-5］，严重影响目标定位。4D-CBCT［6］的出现使得机载目标定位和运动范围得到控制。然而，现有的CBCT成像系统单个阶段投影数量非常低［7-8］，常规解析算法重建［9-10］的图像充斥着大量的噪声和伪影，无法精确定位及三维运动轨迹跟踪，从而影响临床治疗，无法实现精确放疗，可能留下肿瘤复发的隐患和其他毒副作用，所以重建出符合临床诊断需要，高质量的CBCT图像具有重要研究价值。

近年来，学者们相继提出了各种4D-CBCT优质重建算法来降低CBCT图像中的噪声和伪影。其中基于相位相关（RC）重建算法［11-12］利用正则化技术对抗数据稀疏性，尤其压缩感知（CS）理论的算法［13-15］对采样不足的投影数据重建表现出良好的性能，但全采样先验图的运动伪影会被带到待重建图像中，引起运动模糊；基于运动补偿(MC)重建算法［16-17］利用各相位的投影数据相位间运动变形场对运动进行补偿，但由投影数据或者图像本身估计所得的运动矢量场［18-20］（MVFs）直接应用于重建图像,忽略了所得到的运动变形场的一部分是来自于伪影变化，导致运动估计的不准确。除此之外，还提出了很多基于神经网络的新方法［21-23］来提高重建CBCT图像质量。但目前所提出的各种4D-CBCT优质重建算法仍无法直接应用于临床，为降低FDK图像中条形伪影对准确估计运动变形场的影响，为进一步优化MVFs，本文提出了基于鲁棒主成分分析的运动补偿重建方法。我们利用RPCA［24］将FDK图像分解为包含运动信息的低秩部分以及包含伪影和噪声的稀疏部分，然后通过使用基于霍恩&舒克光流法［25］的配准算法估计出低秩图像相位间的运动变形场。该方法不再由投影数据或者图像本身所估计的MVFs直接应于重建图像，而是以图像分解的理论框架为基础，构建基于RPCA分解的图像配准算法，在消除FDK图像中的条形伪影的同时准确估计MVFs。

1 材料和方法

1.1 FDK锥形束图像重建算法

Fe1dkamp等［26］提出一种基于圆轨道扫描的FDK锥形束图像重建算法，该算法是专门为锥形束圆形焦点轨道而设计。FDK算法简单易实现，是CBCT成像系统中普遍使用的重建算法。平板探测器锥形束成像坐标系如图1所示，FDK 算法表达式可表示为式（1）：

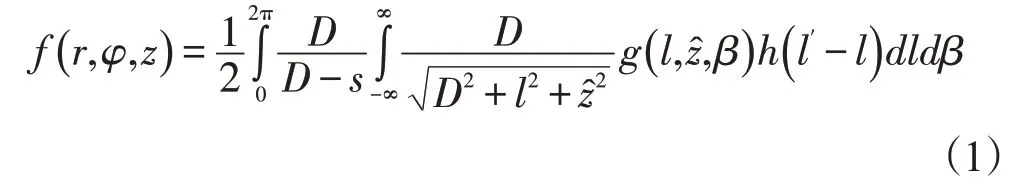
1.2 基于运动补偿的CBCT重建算法

Li等［27］提出了一种将患者特定的运动模型纳入到图像重建中以获得相位分辨CBCT图像的运动补偿重建算法。该算法的运动估计是基于FDK算法重建图像进行的，在本文中简称为MC-FDK算法。MC-FDK算法中假设物体在扫描期间，在每个角度θi获得的投影数据gθi可以描述为其在第一个角度的投影数据g0被时间变换Tθi作用的结果，构建的运动模型如下：

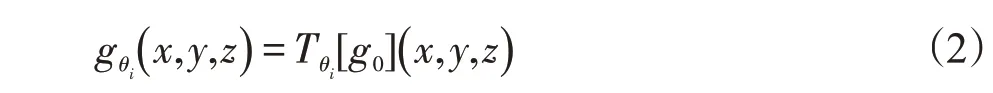
其中i=0,1,...,N-1 N=π/θ，将运动模型纳入到锥形束CT重建时，将FDK表示为加权滤波反投影，构建运动补偿重建模型如下：

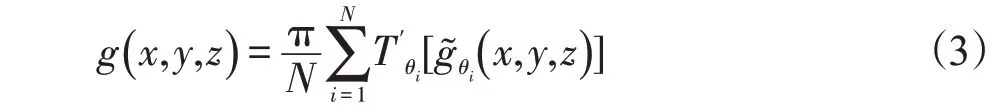
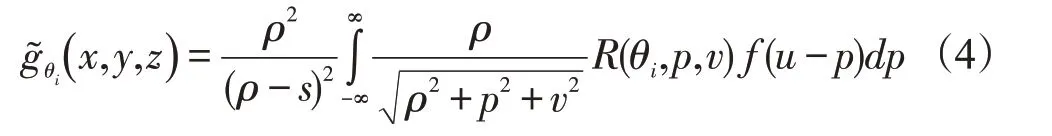
MC-FDK算法对投影数据进行运动补偿重建，可以较好的改善运动模糊。但常规算法的运动估计是基于FDK图像进行的，在4D-CBCT图像重建中，单个呼吸相位下投影数据的数量非常少，使用FDK算法重建的图像中含有大量的噪声和伪影，这就使得运动矢量场的一部分是来自伪影变化，运动估计误差会导致重建图像出现运动模糊和伪结构。为了降低FDK图像中条纹伪影对准确估计运动变形场的影响，本文提出运用鲁棒主成分分析分离出FDK图像中的运动和条纹伪影，对低秩图像进行运动估计。

1.3 基于鲁棒主成分分析的运动补偿CBCT重建算法

Candès等［28-29］提出了鲁棒主成分分析（RPCA）算法，RPCA是实现图像背景与前景分离［30-31］的重要技术之一。RPCA采用低秩模型，将数据矩阵分解为低秩矩阵和稀疏矩阵，即D=L+S，Candès等人已经证明利用RPCA，在满足一些条件时就可以精确地恢复出L 和S。在实际应用中，假设给定一很大的数据矩阵D，它可以分解成D=L+S，当D 中存在大量噪声时，这一分解问题可以表述为一个凸优化问题：

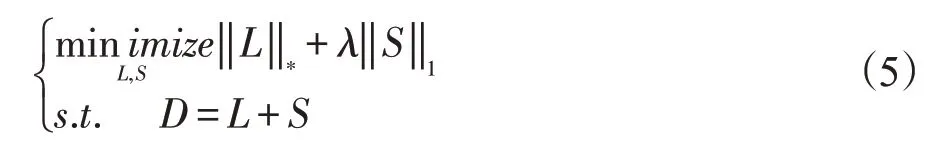
式（5）中‖ ‖L*和‖ ‖S1分别表示核范数（矩阵L 的奇异值之和）和L1-范数（矩阵S 中非零元素的绝对值之和）。其中λ表示平衡因子。如图2所示，在本文中，我们通过鲁棒主成分分析将CBCT图像D 分解为低秩分量L 和稀疏分量S。通过不断调节λ的值，使得低秩部分包含更多的运动信息，也即是在保持运动信息的条件下最大可能的分离出图像中的伪影和噪声。

在运动补偿重建算法中，准确估计运动变形场是关键。本文采用基于霍恩&舒克的光流法［25］对呼吸运动进行估计。光流法的计算是基于图像像素进行的，在精确性和鲁棒性方面有很大的优势。基于亮度恒定的假设：uk(x+v(x))-ur(x)=0，估计图像fk与fr之间光流场v=(u,s,w)T，将待配准的图像按照光流场进行变换：

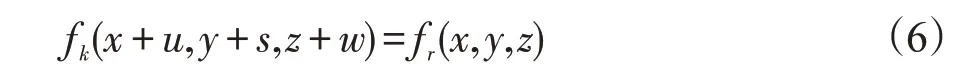
转化为算子形式Mr,kfk=fr，其中r=1,2,…,N ，k=1,2,...,N，N为相位个数。本文中经过RPCA分解得到的低秩图像，同样按照光流场进行变换：

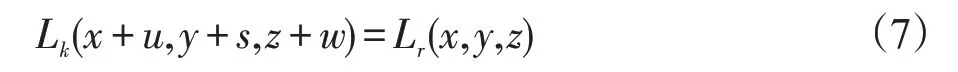
如图3所示，估计运动变形场的过程可以描述为：第一步对投影数据使用FDK算法重建得到CBCT图像D；第二步对CBCT图像进行RPCA分解，以初始值λinit作为平衡参数，调节λ 的值以获取合适低秩分量L；第三步采用基于霍恩&舒克的光流法对低秩图像进行运动估计，得到的运动变形场（MVFs）；重复循环此过程，并调节参数λ的值，让更多的信息出现在低秩分量中。

结合式（7）对低秩图像进行不同相位图像间运动变形场估计。将式（7）转化为算子形式Tr,kLk=Lr，引入不同呼吸相位图像间的相关特性，构建出如下重建模型：

其中fMC(k)表示对应于呼吸相位k的重建图像，gr表示对应于呼吸相位r的投影数据，TRPCA(r,k)为RPCA分离后的运动补偿算子，X-1为FDK重建算子。

1.4 实验数据获取

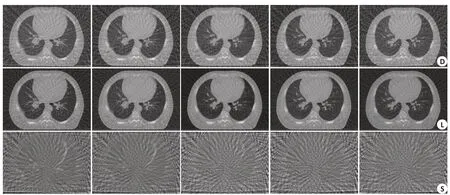
图2 RPCA对不同相位的CBCT图像进行分解Fig.2 Decomposition of 4D-CBCT at different phases with RPCA.From top to bottom:original series(D);low rank component(L);sparse component(S).

分别用仿真数据及临床数据进行算法测试。肺部仿真数据：采用飞利浦16层螺旋CT扫描仪获得的4D CT图像进行数据仿真，仿真成像扫描几何根据瓦里安EDGE加速器选择，X线源到探测器的距离是1500 mm，到旋转中心的距离是1000 mm，投影数据大小为512×384。在本实验中，根据投影数据相位信息，我们将投影数据划分为10个相位。

病人数据：数据采集是利用E1ekta Synergy系统的CBCT扫描系统以半扇模式获得肺癌肿瘤患者的CB投影数据，投影数据大小为924×384，相应像素大小为0.776 mm×0.776 mm。在矩阵256×256×130上各向同性重建目标分辨率为1.5 mm×1.5 mm×1.5 mm。根据投影数据相位信息，我们将投影数据划分为8个相位。

1.5 结果分析

分别使用3种不同的算法重建数据集，第1种是FDK算法，分别重构各相位的投影数据；第2种是MC_FDK算法；第3种是本文提出的基于RPCA分解的运动补偿算法。将我们的重建结果与两种算法进行了比较，除了视觉检查，定量指标也是必要的，为了探讨算法在结构信息保留方面的性能，我们使用结构相似度（SSIM）指数来评价重构后的图像与标准图像之间的相似程度。为了评估算法的性能我们也计算了峰值信噪比（PSNR）。

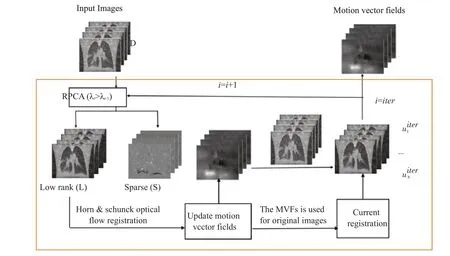
图3 估计运动变形场的流程图Fig.3 Diagram illustrating the estimation of the MVFs.

2 结果

2.1 仿真数据

图4给出了某一呼吸相位的冠状、矢状和横断面的仿真数据重建结果比较。图4A是4D-CT图像，作为对比图像。图4B为FDK 算法重建的图像，我们可以看到重建图像中存在大量的条形伪影和噪声。图4C是MC-FDK算法的重建结果，采用运动补偿算法直接对FDK图像进行的运动估计和运动补偿，相比于图4A噪声得到有效的抑制，图像质量得到进一步提高，但条形伪影没有得到有效抑制。最后一行为本文提出算法的重建结果，可以明显的看出，图像噪声和条纹伪影得到有效抑制，与图4B相比较，条形伪影明显减少，CBCT图像质量得到很大提升，同时没有伪结构引入。

进一步验证本文提出的算法，探讨算法在结构信息保留方面的性能，我们计算了不同呼吸相位下重构图像与真值图像（4D-CT图像）之间的结构相似性。如图5所示，本文算法PSNR与SSIM较MC-FDK算法分别提高了25.4%与7.6%；与FDK 算法相比分别提高了37.9%与17.6%。

2.2 病人数据

图6给出了病人数据5个呼吸相位下的横断面重建结果。利用FDK方法对所有投影数据重建出的8个相位下平均图像，图6A可以看出大部分条纹伪影被消除，但部分解剖结构信息模糊，对于病人数据是没有真实图像的，我们将平均作为视觉参考图像。图6B是FDK 算法重建的结果，可以看出图像中充斥着大量的条形伪影和噪声，很多解剖结构信息被噪声和伪影掩盖。图6C是MC-FDK算法的重建结果，对投影数据进行运动补偿重建，相较于FDK算法重建结果，图像质量有所提升。图6D为本文提出算法的重建结果，可以看出图像噪声和伪影图明显比6B、C减少，CBCT图像质量得到很大提升。图7是相应呼吸相位下的矢状面图像。

3 讨论

常规运动补偿重建算法［18-19,27］由投影数据或者图像本身估计所得的运动矢量（MVFs）直接应用于重建图像，忽略了投影数据或者图像本身存在大量的噪声和伪影［9-10］，这就可能导致所估计的运动变形场的一部分是来自于伪影变化，运动估计的不准确可能导致重建图像中出现伪结构，。本文中，为了降低FDK图像中条形伪影对准确估计运动变形场的影响，我们提出了基于鲁棒主成分分析的运动补偿四维锥形束重建算法。本文算法在传统MC-FDK算法基础上针对运动变形场的估计进行改进，首先利用RPCA［24］将FDK图像分解成低秩分量和稀疏分量，分离出FDK图像中的噪声和伪影得到包含运动信息的低秩分量，然后结合基于霍恩&舒克光流法［25］计算低秩图像不同相位间的运动变形场，实现重构。

图4 某一呼吸相位仿真数据重建结果Fig.4 Reconstruction results of simulated physical phantom data of a selected phase.A:4D-CT.B:FDK reconstruction.C:MC-FDK reconstruction.D:Reconstructions using the proposed algorithm.

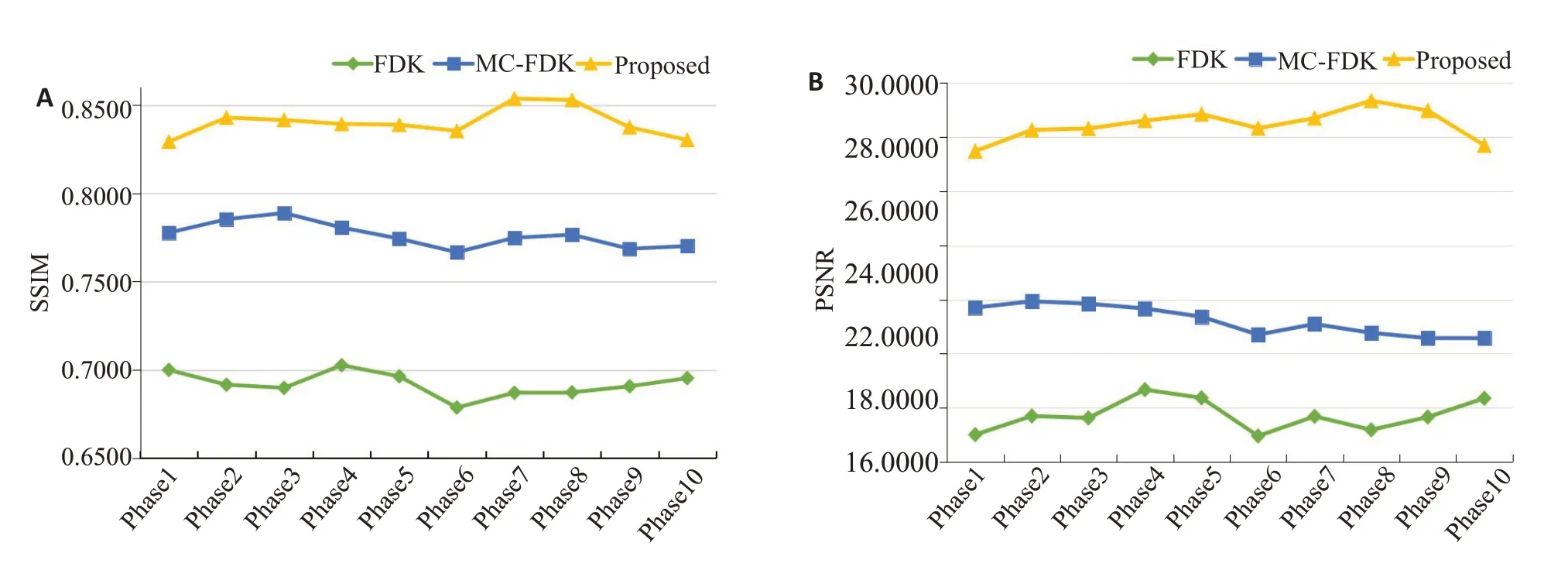
图5 对不同算法重构结果进行定量比较Fig.5 Quantitative comparisons of 4D-CBCT images using the algorithms.A: SSIMs over the image at different phases. B:PSNRs tests at different phases.

运动估计是重建过程中影响算法性能比较关键的一步，运动估计不足会造成重建图像的运动模糊的存在,运动估计过度则会造成重建图像出现伪影伪像。其中RPCA分解是运动估计过程中的关键，RPCA分解效果由参数λ直接决定，λ值不同，稀疏分量中运动信息和噪声伪影占比就不同。λ选取过小，会造成噪声和伪影得到较好分离，但同时运动信息主要出现在稀疏部分，低秩部分运动较小；λ选取过大，会造成噪声和伪影的分析效果差，实验过程中我们发现当λ=0.5±0.1时，获取的分离效果最佳，在保留运动信息的同时可以较好的分离出噪声和伪影，这与Hamy等［24］的实验结果是一致的。同时，在运动信息估计迭代过程中，我们采取λ设置由小变大的原则，将初始值λinit设置为0.4，每次循环加0.1，循环3次结束。图2结果显示RPCA可成功分离出FDK图像中的噪声和条形伪影。图6结果显示，通过所有投影数据采用FDK［26］重建出的平均图像可以消除大部分伪影，但由于投影数据的不一致性导致严重的运动伪影，组织边界模糊；MC-FDK算法［27］可以较好的消除运动模糊，但直接在FDK图像上进行运动估计/补偿，FDK图像中的伪影导致运动估计不准确，图像质量不够好。

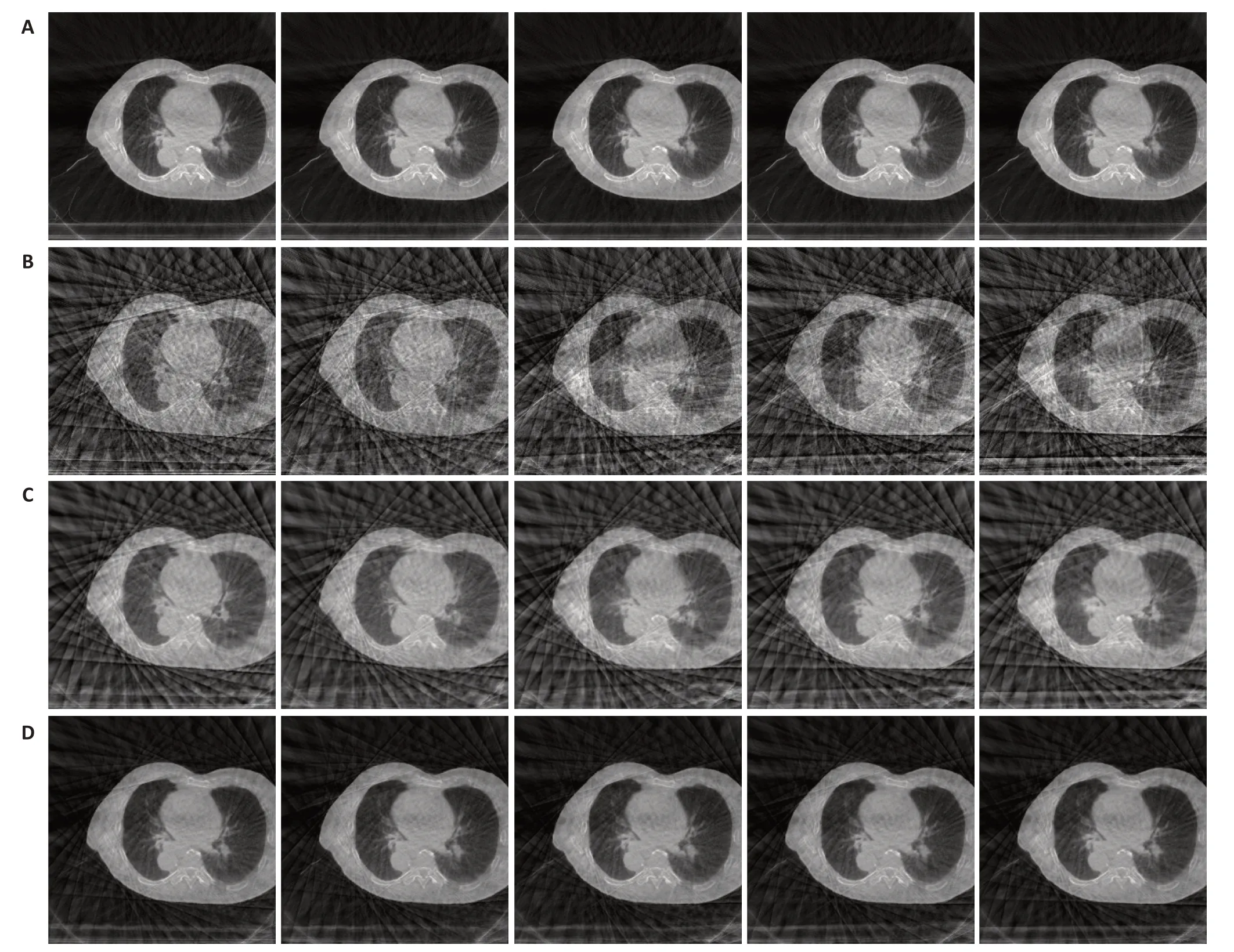
图6 对应于5个呼吸相位的本文算法重建结果的横断面图像Fig.6 Reconstructed transverse images of patient data at 5 phases.A:all phase FDK mean image.B:FDK reconstruction.C:MC-FDK reconstruction.D:Reconstructions using the proposed algorithm.

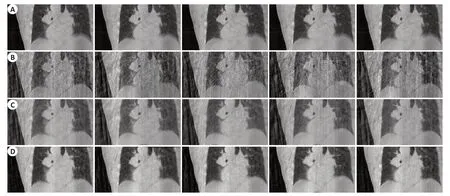
图7 对应于5个呼吸相位的本文算法重建结果的矢状面图像Fig.7 Reconstructed sagittal images of patient data at five phases. A: all phase FDK mean image. B: FDK reconstruction. C: MC-FDK reconstruction.D:Reconstructions using the proposed algorithm.

相对于传统的MC-FDK算法，本文算法以图像分解的理论框架为基础，构建基于RPCA分解的图像配准算法实现对4DCBCT相位间变形场的有效估计。相对于传统迭代重建或者基于运动补偿的迭代重建算法，本文算法是在实现RPCA分解后进行配准，不需要迭代重建过程，计算效率较迭代重建算法［32］有较大优势，整体来说计算量较小，重建时间更短。仿真实验结果和病人数据实验结果对比展示了基于鲁棒主成分分析的运动补偿算法的优越性，从实验结果来看，改进后的方法较MC-FDK算法可更有效的抑制图像中的噪声和伪影，细节对比度和CBCT图像质量均有所提高。

综上所述，本文算法以图像分解的理论框架为基础，构建基于RPCA分解的图像配准算法可以实现对4D-CBCT相位间变形场的有效估计，有效抑制图像中的噪声和伪影，提高CBCT图像细节对比度，所得的重建图像质量优于MC-FDK算法，在肺癌肿瘤CBCT图像重建中的应用为胸部4D-CBCT优质重建提供了一个新方法，同时在4D-CBCT优质重建研究方向上迈进了一步。