基于改进 CNN 的光热电场太阳直接法向辐射预测研究

杨德州， 李锦键， 吕金历， 杨维满， 王兴贵

（1.国网甘肃省电力公司经济技术研究院， 甘肃 兰州 730000； 2.兰州理工大学 电气工程与信息工程学院，甘肃 兰州 730050）

0 引言

太阳能作为新能源发电的主要能源。 合理地使用太阳能， 可以基本满足人类生产和生活的需要[1]，[2]。 由于太阳能是一种具有不确定性的能源，因此， 太阳能发电系统产生的电能在并网时会给电力系统带来较大的冲击。 聚光太阳能发电（Concentrating Solar Power，CSP）也被称为光热发电， 是一种利用太阳辐射中直接法向辐射（Direct Normal Irradiance，DNI）的能量使液态水转化为蒸汽， 并用蒸汽的压力推动汽轮发电机组工作的发电方式。 由于光热发电系统配有能量缓冲作用的储热系统， 可以减轻光热发电系统产生的电能在并网时对电力系统的冲击，因此，光热发电具有广阔的应用前景。 为了使CSP 电站产生的电能在并网时可以充分发挥其优势，且易受电力系统调度，本文须要准确预测决定CSP 电站出力的主要因素—直接法向辐射DNI。

目前， 预测DNI 的手段主要有随机学习法、数值天气预报法、 全天空成像外推法和卫星成像外推法等。 数值天气预报法为通过拟合历史天气预报数据与DNI 之间的关系，并利用人工神经网络等统计方法预测两者之间关系的方法[3]，[4]。作为人工神经网络中的典型模型，BP 神经网络和小波神经网络已应用到DNI 的预测中[5]，[6]。 但在学习时， 传统人工神经网络无法获取数据深层次的特征，因此，会降低预测的准确性[7]。 由Hinton 提出的深度学习模型凭借着强大的特征提取能力，被应用到DNI 预测、风电功率预测和齿轮箱状态监测等研究中[8]～[11]。 由于卷积神经网络（Convolutional Neural Networks，CNN） 能较好地处理具有网格结构的数据，因此，文献[11]，[12]分别利用混沌融合算法和门控循环单元对卷积神经网络结构和学习参数进行优化，并应用到DNI 和超短期风电功率预测中。

为了在实际运行中更好地利用CSP 电站，本文建立了一种基于改进CNN 的光热电场DNI 的预测模型。 首先，本文根据DNI 数据的特点选用CNN 对DNI 进行预测；然后，本文针对CNN 在实际应用中存在的预测精度较低和训练时间较长的问题，在CNN 的训练阶段引入带有稀疏约束的损失函数，使网络结构稀疏化，同时在预训练阶段采用自适应学习率的方法优化网络参数， 并提出一种改进CNN；最后，本文基于改进CNN 建立了光热电场DNI 的预测模型。

1 光热电站运行原理及DNI 特点

1.1 光热电站运行原理

本文对CSP 电站各子系统间的能量流进行简化，CSP 电站基本能量流示意图如图1 所示[13]。

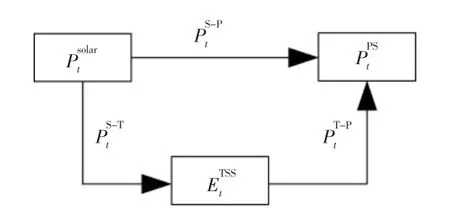
图1 CSP 电站基本能量流示意图Fig.1 The basic energy flow diagram of CSP station

CSP 发电系统的运行原理：SFS 收集太阳能，并将能量通过传热流体 （Heat-transfer Fluid，HTF） 传递至其余各子系统。 当DNI 充足时，由SFS 收集到的能量一部分用于PS 进行发电，另一部分存储到TSS 中；当DNI 不足时，TSS 通过放热的方式释放能量，TSS 放出的能量与SFS 收集到的能量共同向PS 提供满足发电要求的能量；当DNI 的值为0， 即无光照时，PS 所需能量完全由TSS 放热提供。综上可知，影响CSP 电站出力的主要因素为SFS 聚光场的DNI。

1.2 DNI 的特点

时间序列是指一组按照时间顺序进行排列的随机变量，即在等距的采样条件下，对某种随机过程进行观测所得到的结果。 时间序列的数学表达为假设有一随机过程X（t）（t∈T，T=t1，t2，…，tN），则t 时刻对X（t）的观测样本Xti（i=1，2，…，N）为一个时间序列[14]。 DNI 序列是由地面观测点对太阳辐射这一随机变量进行观测和记录得到的，又因为太阳辐射是按照时间顺序进行变化的随机变量， 因此，DNI 序列在数学本质上属于时间序列，从而得知，DNI 具有长期性、季节性、循环性和不规则性的特征，这些DNI 序列特征决定了可以通过CNN 挖掘其数据中隐藏的深层关系，进而实现预测。

2 改进卷积神经网络

作为深度学习网络中监督学习的典型代表，CNN 的基本思想是通过搭建多层感知网络的方法对输入层得到的信息进行多层分解， 根据分解结果获得数据更深层次的隐藏信息， 从而得到比一般人工神经网络泛化性更强的网络。 CNN 通过卷积层获得数据深层次的隐藏信息并减小保存数据所需的内存。 由于卷积操作具有上述特性，因此，CNN 主要应用在处理具有类似网格结构数据的场景中。 隐含层是由卷积层与池化层构成的低层和由全连接层构成的高层组成， 隐含层的结构可以方便CNN 提取网络输入数据深层次的特征。CNN 特有的卷积层、池化层和它们内部的权值共享既可以有效地减少网络参数的数量， 又可以增强网络的泛化能力和鲁棒性[15]。 图2 为以图像识别为例的CNN 典型网络结构演示图。

在CNN 的训练过程中，一般采用BP 算法最小化损失函数和利用迭代训练的策略不断调节网络参数，从而不断提高网络的精度。 但是，在CNN的训练过程中， 大量的冗余网络参数和固定学习率的训练算法会造成网络预测精度较低、 训练时间较长[16]。 为了解决上述问题，须要对传统CNN训练算法进行改进。

2.1 CNN 的稀疏化

文献[16]指出，在CNN 训练过程中，存在大量的冗余网络参数，因此，须要对其中无用的连接权重进行归零，即稀疏化操作。 对CNN 进行稀疏化操作就是寻找一种判定准则， 并以此为准， 剔掉CNN 结构中对输出影响较低的连接和节点，从而提升CNN 的稀疏度。 稀疏化操作可以有效提高CNN 的运行速度，减少网络参数所占内存，从而降低过拟合现象发生的概率[17]。

目前， 稀疏化操作主要包括训练过程中的稀疏约束和训练完成后的剪枝[18]。 本文采用的稀疏化操作是训练过程中的稀疏约束，即在CNN 损失函数中添加稀疏约束项， 以实现训练过程中网络的稀疏化。

带有稀疏约束的损失函数表达式为

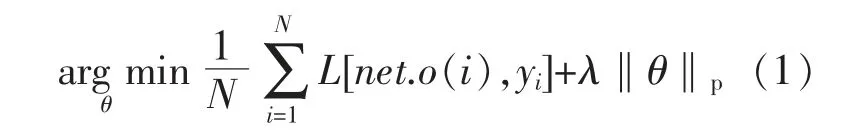
式中：N 为样本总数量；net.o（i）为网络实际输出；yi为网络期望输出；L[net.o（i），yi]为损失函数；λ为权衡范数惩罚的相对贡献项； ‖θ‖p为正则化项，‖θ‖p=（∑i|xi|p）1/p，其中p∈{0，1}。

带有上述正则化项约束的损失函数在反向传播网络参数的调优阶段会使一些不重要的权重连接断开，即权重值为0，从而进一步提升训练完成后的CNN 的稀疏度，提高其泛化性能，降低过拟合现象出现的概率。本文以全连接层为例，说明稀疏化操作对CNN 结构的影响。

稀疏化示意图如图3 所示。

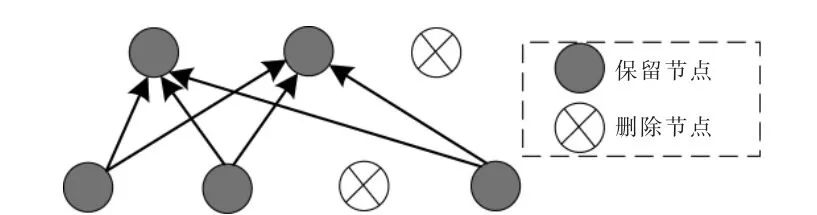
图3 稀疏化示意图Fig.3 The schematic diagram of sparse constraints

2.2 采用自适应学习率的训练算法

2009 年，Raina 提出了自适应学习率思想[19]。文献[20]将自适应学习率思想应用到深度信念网络，分析结果表明，该思想可以有效提高深度信念网络的训练速度和准确性。因此，本文将自适应学习率思想引入到CNN 的训练过程中， 以提高CNN 的训练速度和准确性。

自适应学习率的核心思想为根据连续2 次网络参数更新方向的异同， 使学习率自适应地进行调整。

自适应学习率η 的表达式为

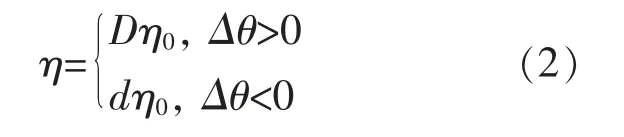
式中：D 为学习率增加的速率；d 为学习率减小的速率；η0为调整前的学习率；Δθ 为网络参数的更新方向。

在CNN 的训练过程中，卷积层的参数更新表达式为

综上所述，采用自适应学习率的CNN 反向参数调优训练算法流程图如图4 所示。

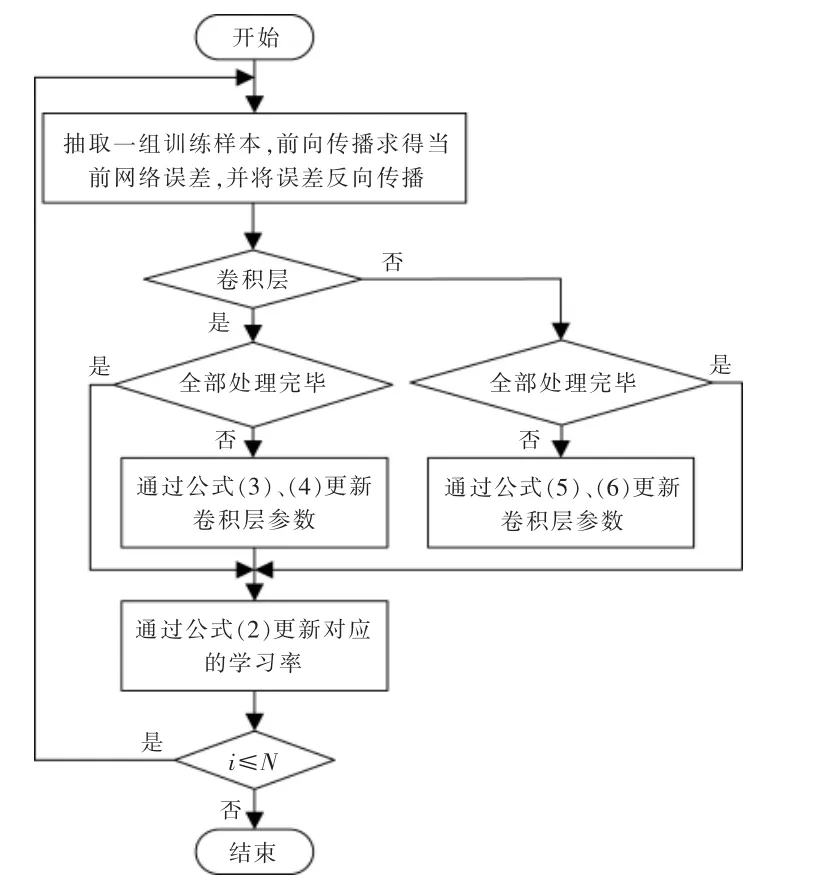
图4 采用自适应学习率的CNN 反向参数调优训练算法流程图Fig.4 The flow chart of CNN reverse parameter tuning training algorithmwith adaptive learning rate

3 预测模型的构建及性能评估

3.1 预测模型整体框架设计

CNN 模型的构建过程主要包括前向传播、BP反向传播、权值更新等步骤。前向传播是将输入层输入的样本按图2 所示的顺序，经过卷积层、池化层和全连接层之后，得到对应的输出向量。 BP 反向传播是利用CNN 实际输出向量与期望输出向量之间的差值，通过BP 算法顺着网络逆向传播，并结合自适应学习率的训练算法对CNN 参数进行调优设置。

本文选用甘肃省敦煌市 （94°E，40°N）2007-2016 年的气象数据作为预测模型学习和预测的样本[21]。本文先剔除原始数据中的异常数据；然后，随机选取500 组数据作为测试样本，其余数据作为训练样本，其中，训练样本用于网络参数优化的训练过程， 测试样本用于测试训练后的网络性能。 为了避免因数据量级差异过大对网络训练速度和预测精度造成不利影响， 本文引入归一化操作，使数据保持在[0，1]之间。 归一化后数据X′的表达式为

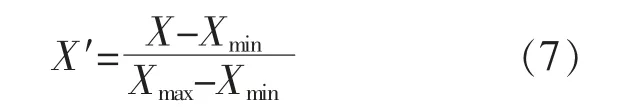
式中：X 为归一化前的数据；Xmin为数据中的最小值；Xmax为数据中的最大值。

基于改进CNN 的预测模型构建过程见图5。

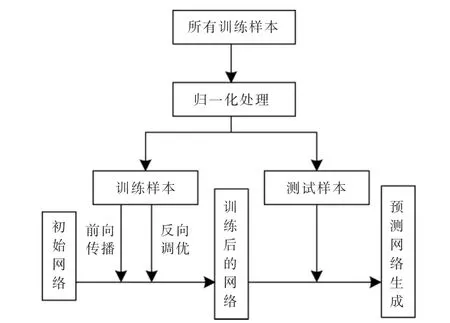
图5 基于改进CNN 的预测模型构建过程Fig.5 Theprocess of building a prediction model based on improved CNN

3.2 预测模型参数设置及评估

本文预测模型的参数设置主要包括网络结构的设置、卷积层参数的设置、隐含层输出特征图数量的设置、全连接层激活函数和损失函数的选择。

预测模型评估主要是评估网络的误差和准确度。

3.2.1 预测网络结构设置

本文基于改进CNN 建立的光热电场太阳DNI 预测模型，是以时间（年份、月份、日期、小时）和其他影响DNI 的参数作为输入向量，以DNI 数据作为输出向量， 对DNI 进行较为准确地预测。其他影响DNI 的参数主要有太阳时角、 气溶胶、水汽、臭氧和云量。 上述9 个参数中，太阳时角和时间（年份、月份、日期、小时）决定了DNI 的基本变化趋势，对预测准确度的影响较大，这5 个参数的影响权重从大到小依次为月份、 太阳时角、小时、日期、年份。 晴天条件下，气溶胶对DNI 预测准确度的影响较大；多云和阴天条件下，云量对预测准确度的影响程度超过气溶胶。 由于水汽和臭氧可以吸收太阳辐射，因此，它们会对DNI 预测的准确度产生一定影响， 但影响权重小于其他几个参数[4]。综上可知，输入向量的维数为9，即输入层神经元的个数为9；输出向量的维数为1，即输出层神经元的个数为1。

为解决上述对输入层的设置和收集到的数据量不足的问题，本文删掉基于改进CNN 建立的预测模型中的池化层， 以避免丢失数据深层次的联系。 由于输入层结构为3×3，因此，本文设置的卷积层为2 层，每层为1 维卷积，以此保证网络预测的准确性。 CNN 最后一层为利用激活函数构建的全连接层， 该层最终得到的输出值即为本文模型反归一化前的最终输出。 考虑到收敛速度和实际应用场景，本文模型选择双曲正切函数tanh（x）作为全连接层的激活函数。 tanh（x）的表达式为

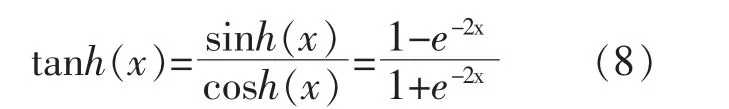
本文模型选择均方误差函数 （Mean-square Error，MSE）作为结构优化的损失函数。其中，MSE表征所有样本误差的平均值L。 L 的表达式为

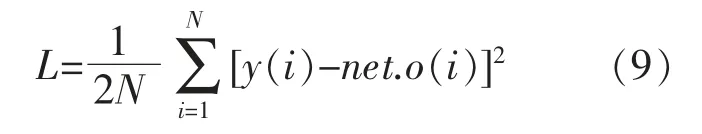
3.2.2 输出特征图数量设置

隐含层输出特征图的数量会影响网络预测精度和训练所需时间，因此，须要对隐含层输出特征图进行择优选择。 本文选择均方根误差（Root Mean-square Error，RMSE）、 平均相对误差（Mean Relative Error，MRE）和平均准确率（Mean Average，MA） 作为预测模型的评价指标和参数选择的标准。 RMSE，MRE，MA 的表达式分别为

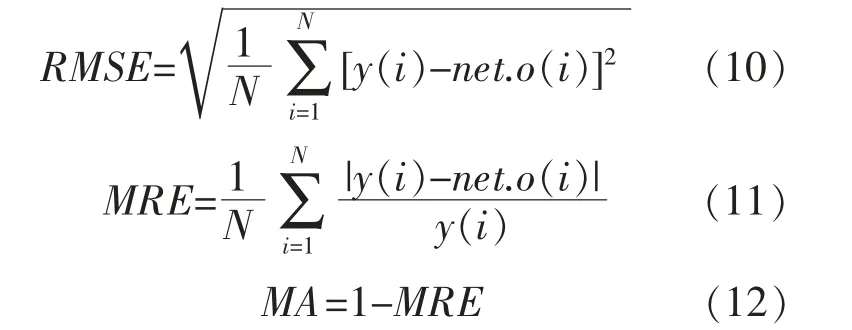
隐含层输出特征图的数量从集合A={100，200，300，400，500}中择优选取。 输出特征图数量（Num）不同时的损失函数收敛曲线见图6。 不同网络参数对应的评价指标和训练时间见表1。

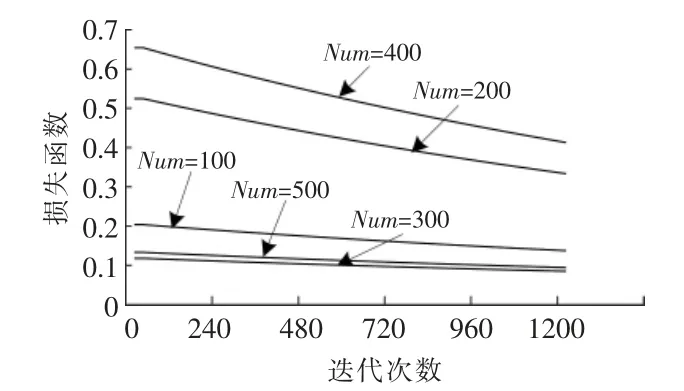
图6 输出特征图数量不同时的损失函数收敛曲线Fig.6 The convergence curve of loss function when the outputmaps take different values

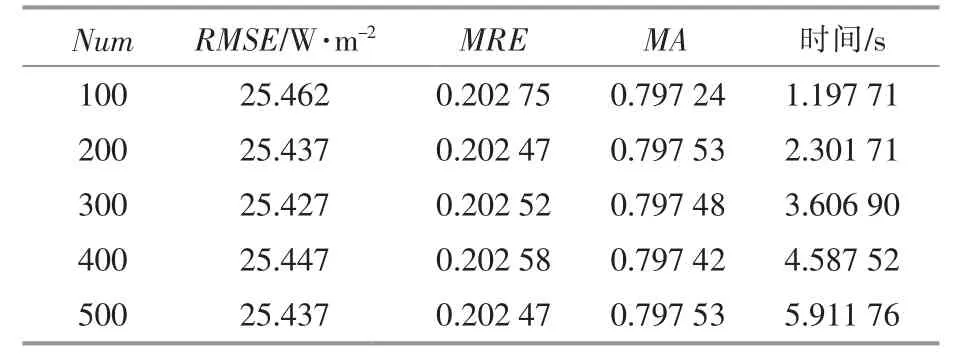
表1 不同网络参数对应的评价指标和训练时间Table 1 Evaluation indicators and training time corresponding to different network parameters

由图6 可知，当Num=400 时，损失函数收敛速度最快， 但此时收敛效果不如其他取值；当Num=300 时， 无论是迭代开始时还是迭代结束时，损失函数均为最小值。 由图6 还可以看出，各损失函数有着收敛于同一数值的趋势， 但是由于训练样本数量不足， 因此， 图中没能呈现出该效果。

综上可知， 在训练样本数量足够庞大的情况下，Num 的取值对损失函数的收敛结果不会产生较大的影响。 由表1 可知，Num 的取值并不会对评价指标产生较大的影响，这是由于随着Num 的增大，RMSE 稳定在25.4 W/m2左右，MRE 稳定在0.202 左右，MA 稳定在0.797 左右，上述各项评价指标均在第3 或第4 位有效数字才出现差别，但是，随着Num 的增大，网络的训练时间逐渐增大。考虑到上述所有因素， 本文设置隐含层输出特征图的数量为300，此时，各项评价指标均满足一般预测的精度要求。

3.2.3 预测网络性能评估

本文基于上述网络参数的设置和对应的评价指标， 对基于一般CNN 的预测模型与基于改进CNN 的预测模型的评价指标和训练时间进行对比，对比结果如表2 所示。

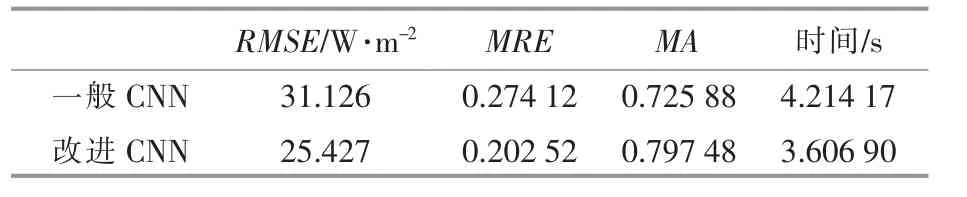
表2 基于一般CNN 与基于改进CNN 的预测模型的评价指标和训练时间Table 2 Evaluation index and training time of prediction model based on general CNN and improved CNN

由表2 可知， 基于改进CNN 的预测模型的RMSE 和MRE 均低于基于一般CNN 的预测模型，即改进CNN 的准确度更高；就训练时间而言，基于改进CNN 的预测模型的训练时间明显少于基于一般CNN 的预测模型，由此可知，改进CNN的训练速度快于一般CNN， 即改进CNN 的训练效率较高。以上结果验证了改进CNN 可以解决一般CNN 存在的预测精度较低和训练速度较慢的问题，同时也验证了基于改进CNN 的预测模型的可行性与高效性。

图7 为改进CNN 在训练完成后，进行测试时误差值随着测试样本数量的变化情况。

图7 改进CNN 在训练完成后，进行测试时误差值随测试样本数量的变化情况Fig.7 The variation of the error value with the number of test samples when the improved CNN is tested after the training is completed

由图7 可知，改进CNN 在训练完成后进行测试时， 误差值稳定在1.8%～2.2%， 且误差值处于1.8%～2.0%的测试样本数量较多。 鉴于上述测试结果和评价指标可知， 本文提出的预测模型满足对精度的要求。

为检测本文预测模型的实际性能， 本文利用该模型预测甘肃省敦煌市2017 年6 月1 日和14日的DNI 的变化情况。 图8，9 分别为2017 年6月1 日和14 日DNI 的预测值与实际值随时间的变化情况。

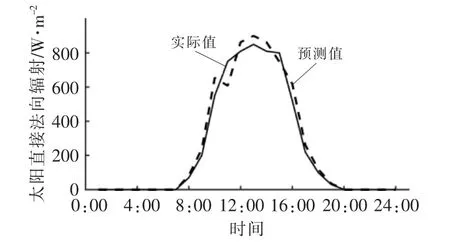
图8 2017 年6 月1 日DNI 的预测值与实际值随时间的变化情况图Fig.8 Predicted versus actual values of DNI over time on Jun. 1， 2017

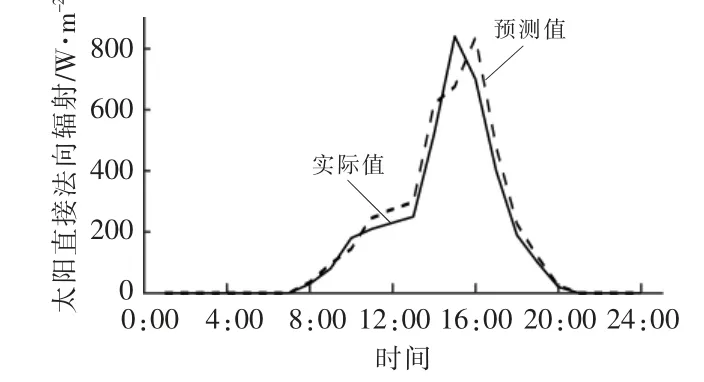
图9 2017 年6 月14 日DNI 的预测值与实际值随时间的变化情况Fig.9 Predicted versus actual values of DNI over time on Jun. 14， 2017

表3 为2017 年6 月1 日和14 日DNI 预测结果的评价指标。

表3 2017 年6 月1 日，14 日DNI 预测结果的评价指标Table 3 The evaluation metrics for DNI forecast results on Jun. 1 and 14， 2017

由图8，9 可知， 本文模型无论在晴朗或是阴转晴的天气条件下， 都可以较为准确地预测出当日DNI 的变化情况。由图8，9 还可以看出，在12：00-16：00 时， 预测值与实际值之间误差较大，这是由于该时段影响DNI 的气象因素复杂的变化规律和耦合关系。此时，较强的太阳辐射会引起空气中水汽浓度、气溶胶浓度、臭氧浓度和云量发生复杂的变化， 上述气象因素的变化又影响地面辐射表的测量值（实际得到的DNI 数值），造成数据变化规律和耦合关系复杂， 进而导致预测结果出现较大误差。由图8，9 和表3 可知，本文模型在预测晴朗天气条件时评价指标较优，即准确度较高。虽然， 本文模型在阴转晴天气条件下预测存在较大误差， 但并不影响该模型预测DNI 的变化趋势， 同时从侧面反映出在阴转晴的情况下， 气溶胶、 水汽、 云量等天气参数的剧烈变化会对预测DNI 数值的准确度产生一定的影响。 由性能检测结果可以看出，太阳时角和时间（年份、月份、日期、小时）决定了DNI 的基本变化趋势，云量等其他气象参数在阴天时会对DNI 的数值造成一定影响，但不会改变DNI 的基本变化趋势，与前文的定性分析基本一致。

综上可知， 与基于一般CNN 的预测模型相比，本文提出模型的预测精度较高、所需训练时间较短。 改进CNN 可以解决一般CNN 在实际应用时存在预测精度较低和训练时间较长的问题。 本文建立的基于改进CNN 的光热电场DNI 预测模型在不同天气条件下均可以较为准确地预测出DNI 的变化趋势及其数值。因此，本文预测模型是可行且有效的。

4 结论

为使CSP 电站得到更合理地应用，以及解决CNN 在实际应用过程中存在的预测精度较低和训练时间较长的问题， 本文建立了一种基于改进CNN 的CSP 电场DNI 的预测模型。 模拟结果表明： 改进CNN 可以解决一般CNN 在应用时存在的预测精度较低和训练时间较长的问题； 基于改进CNN 建立的CSP 电场DNI 的预测模型可以较为准确地预测出DNI 的变化趋势及其数值，且满足对精度的要求。