初中数学课堂分散难点策略的探究

◎ 陈秀萍

在初中数学学习过程中，时常会遇到难度比较大的问题，部分学生看到难题总觉得害怕，不敢尝试，部分学生不知道如何解决，束手无策。一种是畏难心理，一种是没掌握好解决问题的方法。遇到这种情况该怎么办呢？笔者通过以下三道案例，浅谈初中数学分散难点的一些策略和方法。

一、分散难点

七年级下册实际问题与二元一次方程组中有一道探究题：据统计资料，甲、乙两种作物的单位面积产量的比是1∶2。现要把一块长200m、宽100m的长方形土地分为两块小长方形土地，分别种植甲、乙两种作物。怎样划分这块土地，使甲、乙两种作物的总产量的比是3∶4呢？这道题很多学生都觉得头疼，都觉得无从下手。刚好笔者听了一位教师讲解这道题，这位教师分析题意，先画图，然后告诉学生设未知数，接着列方程。整个过程一气呵成，听起来很流畅，没有什么问题，但是课后一问，大多数学生都是懵懵懂懂，详细点问，他们不知道x、y如何去设，不知道等量关系是什么，更不知道如何列方程，遇到类型题完全无从下手。

为什么会出现这样的情况？首先，这位教师只是讲怎样做，并没有讲为什么这样做，更不讲为什么会想到这样做。他是站在教师的角度备课、上课，而不是站在学生的角度备课，没有了解学生哪个知识点不清楚，他们有没有接触过单位面积产量、有没有接触过总产量，知不知道比例的含义。其次，这位教师没有让学生参与探究学习，发挥学生的主体性。解决难题就像吃大螃蟹，使劲啃是吃不到里面鲜美的肉的。那么到底如何解决这道题呢？这道题其实有四个难点：难点一是单位面积产量、总产量的概念；难点二是如何画图，设x、y；难点三是单位面积产量的比、总产量的比的含义，找出等量关系；难题四是列方程。只有把这四个难点一一攻克，才能真正做到水到渠成。

首先，教师课前让学生查找资料，了解单位面积产量指的是平均每单位土地面积上所收获的农产品数量，简称单产，亦称收获率。单位面积产量=总产量÷总面积。为了更好地帮助学生理解，教师可以先举个例子：100 平方米的土地可以生产土豆80 千克，可以生产花生40千克，问土豆、花生的单位产量是多少？这样的问题大多数学生都能解决，有学生还得出结论：这个就像我们的工作效率；然后，教师让学生自己画图，讨论如何分区域种植，有学生横着分，有学生竖着分，究竟怎样分更好，学生展开讨论，顺利设出了x、y；接着，了解比例的性质a∶b=c∶d可化成a÷b=c÷d、ad=bc，从而找出等量关系；最后，由图形得x+y=200或者x+y=100，由总产量=单位面积×总面积得出100x∶(2×100y)=3∶4 或200x∶(2×200y)=3∶4，这时问题才真正解决。学生通过这道例题体会到了数学在生活中的实际应用，学会了从多种角度考虑问题，发现了数学的趣味性。

二、降低难度

已知xy＜0，化简。这道题的解答过程也简单。

解：∵xy＜0，x2y＞0

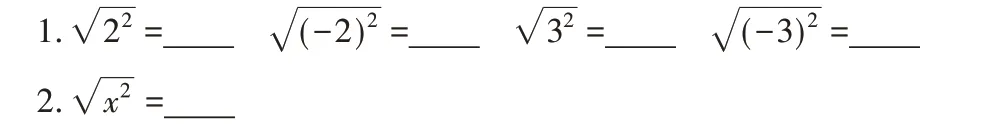
用第1 小题作为第一台阶，学生稍加思考就很容易到达第二台阶，从而顺利解决这道题。如果没有这两个小题作为台阶，只是直接解题，学生就会理解不够透彻，再次遇见这种题型就容易出错。

三、设置梯度

如图，已知△ABC中，BD、CE分别是△ABC的两条角平分线，相交于点O，∠A＝x°，求∠BOC。(用含x代数式表示)

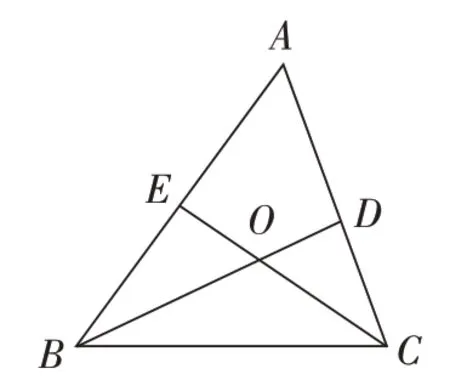
题目难点一：∠A没有具体的度数；难点二：发现∠BOC与∠ABC、∠ACB的关系。对此，教师可以先设计两道题当台阶，分散难点，帮助学生在教师的引导下一步步解决问题。

1.当∠ABC=60°，∠ACB=80°时，求∠BOC；(解决难点二)

2.当∠A=40°时，求∠BOC；(解决难点一)

3.当∠A=x°时，求∠BOC。(用含x代数式表示)

解：1.∵BD、CE分别是△ABC的角平分线

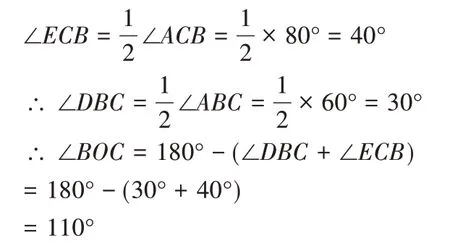
2.∵BD、CE分别是△ABC的角平分线

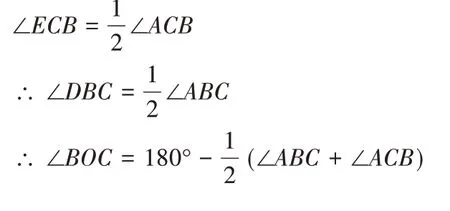
3.∵BD、CE分别是△ABC的角平分线

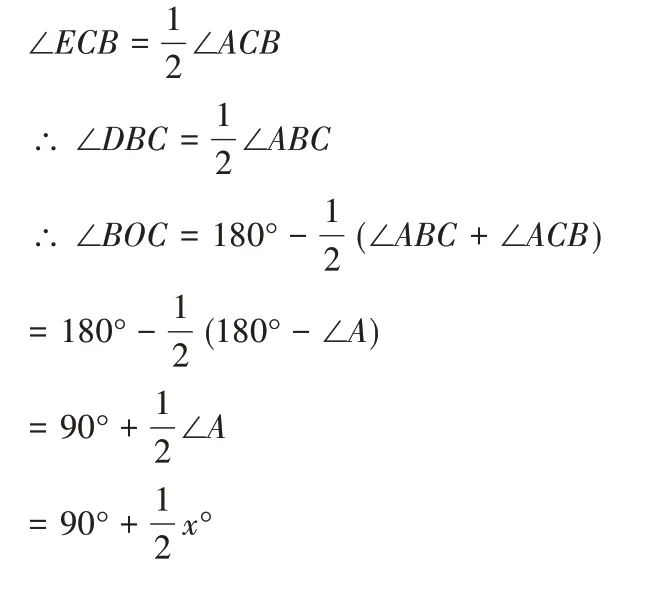
一道难题的综合知识面广，教师要查漏补缺，为学生解决问题扫清障碍，同时也要发现易错点，引导学生反思题目运用了哪些知识点，培养学生的归纳总结能力，从而提高其解题能力。

四、结语

总而言之，解决难题一般是把一个问题分成若干个容易的问题，这就是我们常说的分散难点。教师最根本的任务是引导学生自主探索，动手操作，培养学生的数学思维能力，使学生全面而深刻地了解探索的过程，并运用自己的理解能力解决问题，这样学生自然能学好数学，难题也不再难了。