新课改下高中数学几何教学的现状与对策分析

2021-02-26王大鹏

中学课程辅导·教学研究 2021年33期

◎ 王大鹏

新课改下，最新版高中数学课程标准对高中数学几何教学做出了全新的教学要求，教师在教学几何知识的同时，应培养学生的空间想象、逻辑思维以及知识应用等能力。但事实上，我国当前的高中数学几何教学效果十分差，几何知识的抽象性与复杂性使得学生思维混乱，学习积极性迅速下降。因此，为贯彻新课改要求，实现对学生能力的培养，本文结合当前高中数学几何教学现状对几何教学的有效开展提出了几点对策，仅供大家参考。

一、新课改下高中数学几何教学现状

作为高中数学的重点教学内容，几何知识是高考的必考项目。但在实际教学中，由于教学方式单一、教师的绝对领导以及学生空间想象力的缺乏，使得当前高中数学几何教学效果并不理想，还有部分教师开展的几何教学根本就是在照本宣科，这样不仅严重打击了学生的学习积极性，还会造成学生思维的形式化、固化，不利于学生空间想象力、逻辑思维以及实践应用能力的培养与发展，甚至会限制高中数学教学的长远发展。为此，教师应该彻底改变这一现状，贯彻新课改要求，转变教学思维与方式。

二、新课改下高中数学几何教学的有效对策

1.深入钻研数学教材，化抽象为具体

高中数学中的几何教学要求学生具备一定的空间想象能力与逻辑思维能力。因此，教师要基于高中数学教材，借助相关实物模型，帮助学生完成感性认识—理性认识的转化，促进课堂教学效率的提高。

例如，在进行高中数学人教A 版《简单几何体的表面积与体积》中“球体”这一知识内容的教学时，教师就可以借助实际的几何球体模型与多媒体信息技术展开教学。教师首先可以播放多媒体视频让学生观察排球、足球或篮球等球形照片，然后引导学生结合自己所看到内容对球体的特征进行描述和表达。学生在初中已经学习过关于圆的平面几何知识，因此在描述球体的特征时，学生普遍认为球体都是圆形的。这个时候，教师就可以向学生提出问题：怎么表示立体的圆？学生思考后回答用“球体”表示。接着，教师可以再次借助多媒体播放有关“圆旋转一周形成球”的动画视频，以此引出球体的概念。视频播放完之后，教师可以利用实物球体模型加深学生对球体的认识，随后引导学生结合实物描述球体的几何概念，以此降低其学习难度。

2.增加学生动手操作机会，发挥学生主观能动性

在高中数学几何教学中，教师要想提高课堂教学有效性，实现对学生各项能力的培养，就必须要注重学生的课堂主体地位及其主观能动性的发挥，鼓励与引导学生自主学习、思考和探索，采用小组合作学习模式让学生结合自身所学知识完成对新知识的学习与探索。

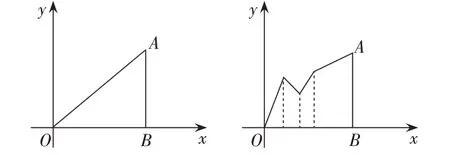
例如，在进行高中数学人教A 版《信息技术应用曲边梯形的面积》这一知识内容的教学时，本节课的教学目的在于让学生体会无限分割思想，能够将曲线围成区域的面积转化为矩形面积的和，以此求出曲边梯形的面积。在实际教学中，教师可以借助小组合作学习模式开展教学，并借助多媒体展示以下图形，并让学生通过自主思考与小组合作，探讨应该怎样求出以下图形的面积，从中可以得到什么启示。这样的教学方式既充分保证了学生的课堂主体地位，又很好地引出了本节课的教学重点内容，让学生自主掌握采用分割的方式将曲边梯形分割成不等分矩形，进而求出面积的方法。

3.丰富学生立体几何解题方法

众所周知，很多数学问题可以根据看待问题的角度产生多种解题方法，特别是高中几何问题，更是有着多变的解决方式。正所谓“授人以鱼，不如授人以渔。”教授学生解决问题的方法，不如教授学生解决问题的技巧，使其能够独立解决问题。因此，在日常教学中，教师应该引导学生从不同的维度看待问题、解决问题，并引导学生总结解决问题的方法与技巧，这样一来，既能有效培养学生的知识应用能力，又能帮助学生更好地解决日常学习中遇到的问题。

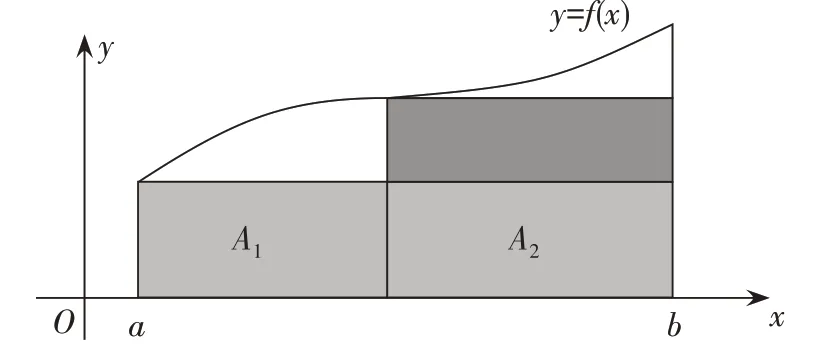
例如，在进行高中数学人教A 版《曲边梯形的面积》这一知识内容的教学时，除了日常几何教学中所常用的无限分割解法之外，求曲边梯形面积的方法还有很多种，如二重积分面积求法、概率几何面积求法、复变函数度量面积求法等等。为了让学生掌握上述多种面积求法，教师可以以一个最为简单的曲边梯形面积计算题为例(如下图)，以此引导学生探索多维解题方法。