铝合金纯III型裂纹断裂韧性实验及数值模拟研究

徐志强,任毅斌,胡国强,宋小雨,刘云刚

(中铝材料应用研究院有限公司,北京 102209)

金属材料裂纹的断裂韧性研究一直是工程中的重要研究课题之一[1],而金属材料被广泛应用在航海、航空、航天、机械加工,生产等各领域中,铝合金材料在应用过程中由于断裂韧性较低,当存在加工缺陷时,常导致断裂事故发生[2],因此测定铝合金材料的断裂韧度显得尤为重要。目前有关铝合金断裂的研究主要集中在对I型裂纹的研究[3-8],对于II、III型裂纹的扩展研究相对较少。

本研究通过对铝合金材料进行扭转实验以使裂纹沿III型裂纹扩展,通过经验公式得到III型裂纹实测的断裂韧性。采用有限元理论对III型裂纹进行数值模拟,并根据断裂力学理论推算出铝合金的Ⅲ型裂纹的断裂韧度。通过对两种方法得到的断裂韧性进行对比,获得实测值与数值解的一致性,这可为铝合金抵抗III型裂纹断裂破坏提供依据。

1 铝合金断裂扭转实验

1.1 实验过程

本实验采用的试件及实验系统如图1所示。其中试件为圆柱形的6061-T6铝合金材料,试件直径D=2b=12 mm,高度L=180 mm,试件中部沿周向开环绕裂纹,裂缝宽度约为1 mm,裂纹尖端大致为矩形端口,中间的圆颈半径a为4 mm,铝合金材料的力学性能参数见表1。

图1 铝合金试件及扭转实验系统

表1 铝合金的力学性能参数

先用实验机两端夹头夹住试件的两端,并固定实验机的下底端保持不动,旋转上端夹头,使上下夹头有一个初始的旋转角度,初始角θ为270°。实验按照角位移加载方式进行加载,角速度ω为27°/min,直至试件发生断裂结束。实验过程中扭矩与扭转角的实验曲线如图2所示,最大扭矩见表1所示。

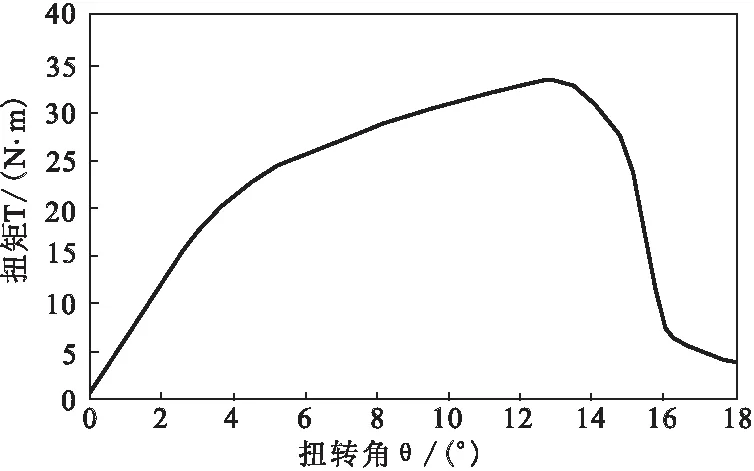
图2 T-θ实验曲线

1.2 实验测试计算结果

由应力强度因子手册[9]可得,对如图3所示的外半径为b,内半径为a的周边裂纹试件,当作用扭矩为T时,可取

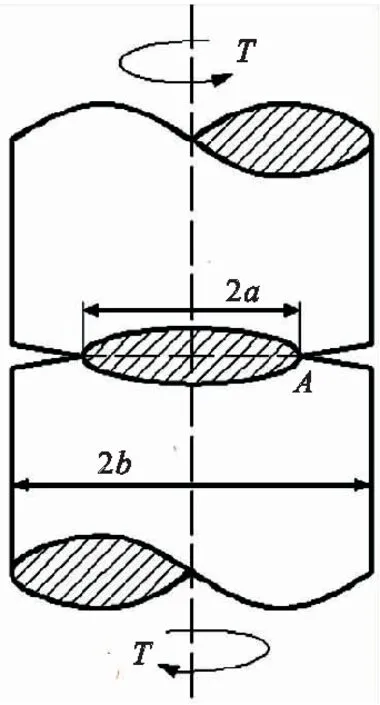
图3 III型裂纹试件

(1)

式中:τn——与扭矩T及内径a有关的剪应力因子。

此圆周裂纹前缘上各点的应力强度因子为:

KIC=KIIC=0

(2)

(3)

(4)

图与曲线

(5)

由式(3)、(4)、(5)可得到KIIIC的表达式:

(6)

联立式(1)、(6),将实验得到的扭矩T值以及试件的内径a和外径b同时代入,即可得到KIIIC值,求得的KIIIC值,见表2。

另外,根据图4中的曲线,可对该曲线进行拟合,并得出对应的拟合曲线方程：

(7)

由此,可得出KIIIC的另外一个表达式,即

(8)

联立式(1)、(8),将实验得到的扭矩T值以及试件的内径a和外径b同时代入,即可得到KIIIC值,求得的KIIIC值,见表2。

2 有限元计算

2.1 有限元建模

本研究按铝合金试件实际尺寸建模,中部裂纹采用1 mm 的环形细缝代替,采用自由网格划分。由于裂纹尖端前缘存在应力集中,因此对裂纹尖端前缘网格进行细划分,以得到较精确的应力值,具体划分情况如图5所示。

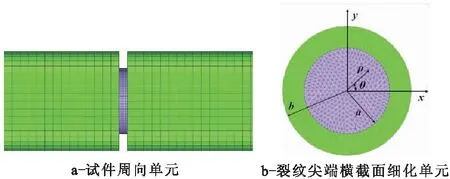
图5 划分单元

在有限元模拟分析过程中,为使模拟与试验保持一致,对距离圆柱试件端部10 mm的所有圆周节点施加全约束。同样地,将距离圆柱试件另一端端部10 mm的所有圆周节点耦合于中间一点,并对该点施加起裂扭矩T。这样施加的约束与载荷与实际的试验情况相符合。

2.2 有限元计算

通过有限元计算分析,得出裂纹尖端附近的应力场,由于该计算模型为柱形杆的扭转,属于轴对称问题,因此,对于这种撕开型的裂纹,可以根据ρ位置处的环向剪应力τzθ与裂纹尖端距离r=a-ρ的关系,来外推出应力强度因子KIII值[10],具体公式为式(9)所示。

(9)

对于圆柱体的扭转,按照弹性力学的方法[11],可将τzθ向Ox轴和Oy轴方向分解,得

(10)

本文通过定义路径选取y轴上的剪应力,此时,θ=90°,所以式(10)可记为

(11)

计算所得半径为a的韧带圆域的剪应力τzx云图如图6所示,沿所选路径的剪应力曲线如图7所示。由图7可知,试件中心(x,y)=(0,0)位置处剪应力为0,在上下两端y=4 mm及y=-4 mm 处裂纹尖端处,剪应力一正一负趋于很大,成反对称分布。

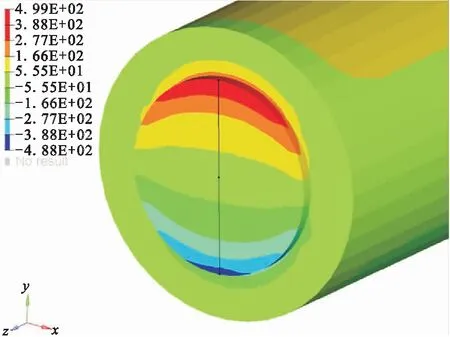
图6 剪应力τzx云图

图7 τzx沿y轴分布值

将式(11)代入式(9)中,可得:

(12)

将定义路径上的剪应力τzx的值代入上式,计算出的各点的应力强度因子值在KIII-r平面中几乎在一条直线上。该拟合直线与KIII纵轴的交点就是通过该扭矩T而算得的KIIIC值。

2.3 实测值与有限元计算结果比较

对表2中的数值解与理论解比较,可以看出数值解与理论解相差不大,并且它们的相对误差为:

(13)

式中:KIIICi——本文得到的实测解,其中i分别对应式(6)、(8)两种计算方法,取i=1,2;

KIII——有限元数值解。

由式(13)可以得出相对误差,具体值见表2。

表2 试件的断裂韧度值

从表2中可看出试件两种计算结果相对误差都在10%以内,说明通过模拟获得的断裂韧度与实测值整体吻合。

3 结 论

本研究主要是对纯III型裂纹进行了实验及数值模拟研究,并根据实验破坏扭矩以及数值计算,得到了III型裂纹起裂的KIIIC值。

(1)对纯III型裂纹进行了扭转实验,并通过应力强度因子手册计算出裂纹起裂时的KIIIC值。

(2)建立圆柱形中部含环形裂纹的试件模型,进行有限元分析,结合断裂力学理论,通过模拟分析计算出裂纹起裂时的数值KIII。

(3)对实测值与数值解进行比较,得出两种方法计算出的KIII值相对误差均在10%以内,基本一致,该结果可为以后其他材料III裂纹断裂韧性的求解提供参考。