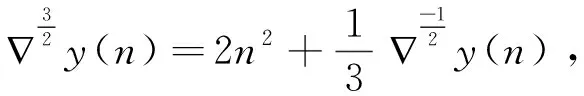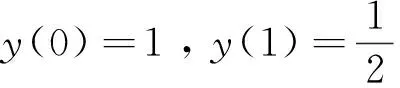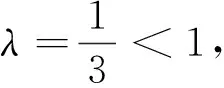一类Riemann-Liouville型混合分数阶差分与和分方程解的存在唯一性
2021-02-26张晓锐王良龙
张晓锐, 王良龙
(安徽大学 数学科学学院,安徽 合肥 230601)
引言
17世纪末,数学家Leibniz和L’Hospital首先对整数阶导数以及整数阶微分方程进行了一次灵魂深处的探讨,如果把整数阶微分方程进一步推广,可以得到细分的分数阶微分方程,甚至是复杂的复数微分方程[1]都是非常有意义且具有挑战性的一件事。随着科学技术的突飞猛进,分数阶微分方程理论的研究和应用变得非常广泛且研究成果颇丰[2-3],其中Riemann-Liouville型和Caputo型这两类初始条件下的分数阶微分方程解的存在性、唯一性、连续依赖性和结构稳定性的研究极具代表性。另外,分数阶微分方程在信息工程、计算机、电路理论等学科也有着非常重要的应用。
众所周知,要想获得一般的分数阶微分方程解的解析表达式或精确表示是比较困难的。考虑将分数阶微分方程离散化以后,我们可以得到相应的分数阶差分方程,从而使我们的分数阶差分方程的研究得到了延伸。我们从方程的发展史得知分数阶差分方程理论的研究相对于分数阶微分方程来说略微滞后,但是近年来涌现出的大量文献使得分数阶差分、分数阶和分的理论研究逐渐完善[4],尤其是差分方程的局部解与非局部解的存在唯一性、多解的存在性、吸引性等方面的研究受到广大研究学者的亲睐[5-8];更重要的是分数阶差分方程在物理学的悬链线振动方程以及生物制药等领域具有非常广泛的应用。特别提到我国学者程金发教授开拓的一种全新的分数阶差分方程理论[9],给本文研究分数阶差分方程提供有力的理论支持。
2017年,何超[10]研究了下列分数阶差分方程的初值问题
αy(n)=f(n,y(n)),n∈[0,N],
y(0)=η,y(1)=φ,
这里1<α<2。f:[0,b]N0×R→R是连续函数,在一定条件下,构造与之等价的Volterra和分方程,再利用迭代法结合Gronwall不等式,得到了解的存在唯一性。
本文研究如下一类Riemann-Liouville型混合分数阶差分与和分方程的初值问题
αx(n)=f(n,-βx(n))
(1)
y(0)=φ,y(1)=ψ,
(2)
这里1<α2,0<β<1,1<α+β<2,n∈[0,b]N0,f:[0,b]N0×R→R是连续函数,φ,ψ是常数。在一定条件下,我们建立了与之等价的Volterra和分方程;并运用Banach压缩映射原理得到了解的存在唯一性;同样运用逐次迭代思想和Mittag-Leffler函数以及Gronwall不等式,得到了解的存在唯一性。
1 预备知识
本文沿用程金发的分数阶微分方程理论[9]的记号与定义。
设a,b为整数,且a 定义1.1假设k∈N+为非负整数,定义x(n)的一阶向后差分为 x(n)=x(n)-x(n-1), 定义1.2假设k∈N+为非负整数,定义x(n)的一阶向后和分为 定义1.3假设μ>0,m=-[-μ],定义x(n)的μ阶差分为 μx(n)=m-(m-μ)x(n)。 定义1.4假设v>0,定义x(n)的v阶和分为 引理1.5假设p>0,m=-[-p],则x(n)的p阶和分有下列计算公式 引理1.6假设p>0,m=-[-p],q∈R,那么x(n)的混合差分与和分有如下性质 引理1.7假设α,β∈R+,λ∈C,记Mittag-Leffler函数为 引理1.8假设v>0,u为实数,则 引理1.9(分数阶Gronwall不等式)假设β>0,un,an,为非负数列,且0b1,如果 unan+b-βan, 那么 un-kβan。 特别地,当an≡0时,则un≡0。 引理1.10(Banach压缩映射定理): 设Y是Banach空间,T:Y→Y是一个压缩映射,则T在Y上有唯一不动点。 定理2.1初值问题(1)(2)的解等价于方程(4) (3) 的解,其中b1=φ-(α-1)φ-f(0,φ)-f(1,φ+βφ),b2=αφ-φ+f(1,φ+βφ)。 (4) -αy(n)=α+β-βy(n)=f(n,-βy(n)), (5) 对(5)两边作α+β阶和分, (6) (7) 由初值条件(2)可知,b1=φ-(α-1)φ-f(0,φ)-f(1,φ+βφ)。 同样可知,b2=αφ-φ+f(1,φ+βφ),将b1,b2代入(6)可得(3)。 =f(n,-βy(n))。 于是(1)得证。当n=0时,代入(3.5)得到y(0)=φ,当n=1时,代入(7)得到y(1)=φ,于是(2)得证。 定理2.2设f满足Lipschitz条件,即存在非负常数L,使得 |f(n,z1)-f(n,z2)|L|z1-z2|, 证明设B={y:[0,b]N0→R},定义‖y‖=max{|y(n)|,n∈[0,b]N0},则(B,‖·‖)为一个Banach空间。在B上定义算子如下 显然,若y∈B为T的不动点,则y为初值问题(1),(2)的解。 事实上,直接计算可得 骨转移的肿瘤患者发生骨相关事件(SRE)的风险明显增加,而SRE的发生与患者生存时间降低显著相关。Sathiakumar等统计了98260例老年乳腺癌患者,有3319例发生SRE,发生SER和未发生SRE的患者死亡风险比分别为6.2和4.9[10]。临床上能观察到骨转移引起病理性骨折、脊髓压迫等骨相关事件后,疼痛、马尾综合征、截瘫等问题严重影响患者的生活质量,长期卧床继发深静脉血栓、肺栓塞、压疮、坠积性肺炎等一系列问题,缩短了患者的生存时间。我们的研究结果也显示,有病理性骨折和脊髓压迫症是影响食管癌骨转移预后的独立危险因素。 |(Ty1)(n)-(Ty2)(n)|=-α|f(n,z1(n))-f(n,z2(n))| 由假设条件可知,T:B→B是压缩映射。又由引理1.10知,T有唯一不动点y(n),此y(n)即为初值问题(1),(2)的唯一解。 定理2.3若初值问题(1),(2)满足以下条件 (1)|f(n,z1)-f(n,z2)|L|z1-z2|,0 (2)|f(n,z)|A|z|+B,z∈[0,], 则初值问题(1)(2)存在唯一解。 证明先证存在性。构造迭代数列 yk(n)=y0(n)+-αf(n,-βyk-1(n)),k=1,2,… |y1(n)-y0(n)|=|-αf(n,-βy0(n))| 同理可得 |y2(n)-y1(n)|=|-α[f(n,-βy1(n))-f(n,-βy0(n))]| 假设有 |yj-1(n)-yj-2(n)| 则有 |yj(n)-yj-1(n)|=|-α[f(n,-βyj-1(n))-f(n,-βyj-2(n))]| 下证唯一性。假设初值(1.1)(1.2)存在两个解y1(n)和y2(n),则有 其中记号D,Dj等见文献[10]。将上述两式相减便得到 |y2(n)-y1(n)|=|-α[f(n,-βy2(n))-f(n,-βy1(n))]|L-(α+β)|y2(n))-y1(n))|, 由分数阶离散Gronwall不等式知,y1(n)≡y2(n),所以解是唯一的。 求解下列差分方程的初值问题 (8) (9) (10) (11) 由定理2.3结合题意,可以构造如下数列 yk(n)=y0(n)+-1.5f(n,-0.5yk-1(n))+2-1.5n2, 于是 y1(n)=y0(n)+-1.5f(0,-0.5y0(n))+2-1.5n2 同理 y2(n)=y0(n)+-1.5f(0,-0.5y1(n))+2-1.5n2 由数学归纳法得 当k→,得到显示解如下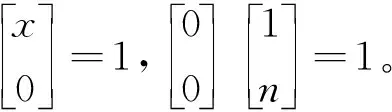
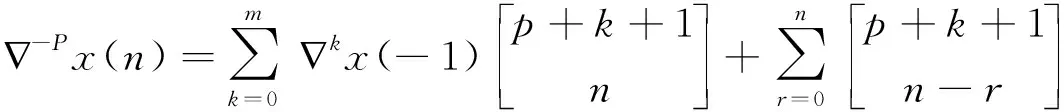
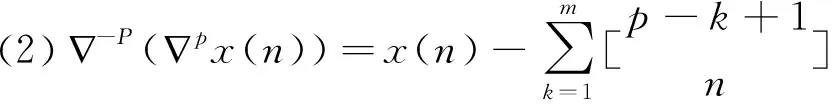
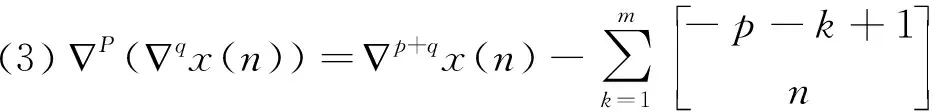
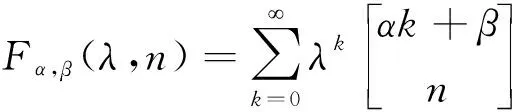
2 主要结果
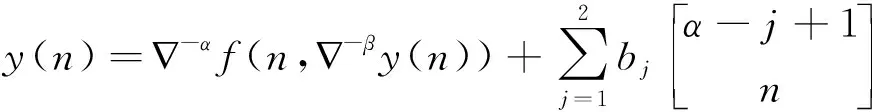
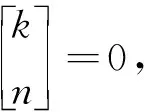
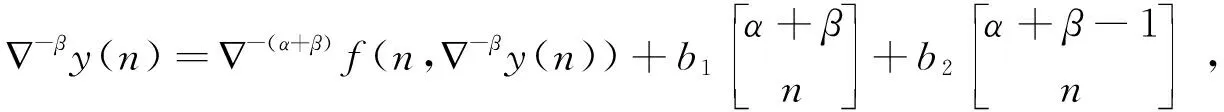
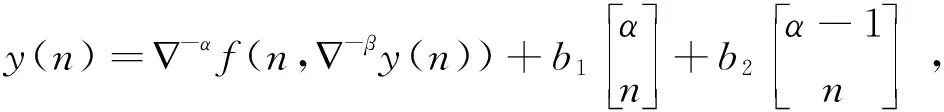

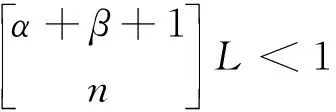

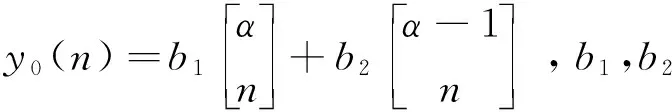
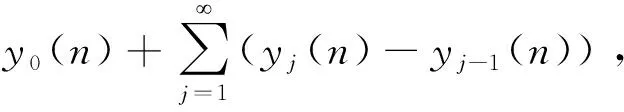
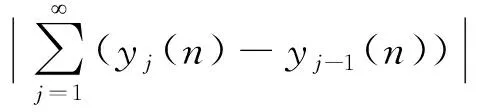


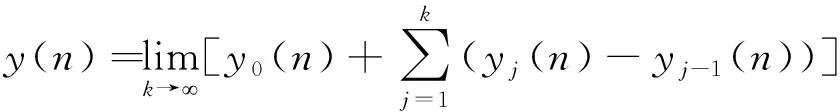
3 例题