船舶电力系统暂态稳定性的仿真与对比分析∗

陈诗涛 卢俊杰 王静绮 李含其 蔡 涛

（1.大连船舶重工集团有限公司 大连 116083）（2.华中科技大学电气与电子工程学院强电磁工程与新技术国家重点实验室 武汉 430074）（3.中国舰船研究设计中心 武汉 430064）

1 引言

船舶电力系统是船舶系统的重要组成部分。随着超大功率的用电设备在船舶上应用越来越广泛，因此要求船舶电力系统的容量也越来越大，以满足用电负荷的需求［1］。同时随着用电设备的增多，船舶电网复杂程度的增加，影响系统稳定性的因素也越来越复杂，对船舶电力系统的稳定性要求也越来越高，因此，稳定性问题成了亟待解决的问题，尤其是暂态稳定性问题更是研究热点的核心［2］。

船舶电力系统的暂态稳定性是指船舶电力系统在正常运行时受到瞬时出现而后又马上消失的扰动后，恢复到原有运行状况附近的能力；或者虽然这种扰动不消失，但是随后系统从扰动后的运行状况安全地过渡到新的稳定运行状态的能力［3］。引起船舶电力系统较大扰动的原因主要有如下几个方面［4］。

1）负载的突然改变，如投入或切除压载泵、侧推器、空压机、锚机、绞缆机、舵机等大容量异步电机的瞬间；

2）电力系统的短路故障，其中三相短路故障对系统造成的危害最大。

基于此，本文将从投切大负荷和短路故障两个角度来做暂态稳定性的分析。

船舶电网结构形式多样，其中基本的配电系统结构有馈线式配电方式、干线式配电方式、混合式（辐射形）配电方式、环形配电方式、网形配电方式［5］。目前针对于大型船舶电力系统，技术较为成熟并且系统供电可靠性较高是辐射形配电方式和环形配电方式。而目前关于这两种拓扑的对比分析比较少，本文将从在短路故障下左右舷配合供电的角度来对这两种拓扑的暂态稳定性进行对比仿真分析。

PSAT是一种基于Matlab的电力系统静态和动态分析及控制工具箱。它的主要功能由潮流分析、连续潮流计算、最优潮流、小信号稳定性分析和暂态稳定时域仿真等。为了提高分析准确性，PSAT提供了大量的静态和动态模形，包括母线、传输线、断路器、变压器、同步电机、感应电机等，而且包括大量使用工具：构造网络的Simulink库、设置参数的图形界面、用户自定义模块工具、数据格式转换及命令记录工具等［6］。

2 PSAT时域仿真法

目前暂态稳定分析主要采用直接法或时域仿真法，PSAT暂态稳定分析通过时域仿真法实现。前向欧拉法和隐式梯形积分法是时域仿真实现的基础，本文采用隐式梯形法［7］。描述隐式梯形法积分过程，对描述系统的微分代数方程差分化：

式中，xn、y（n已知量），xn+1、yn+（1待求量），分别是t=tn、tn+1时刻系统状态变量和代数变量值，f(xn'yn)代表微分方程，g(xn'yn)代表代数方程。Δt=tn+1-tn，是仿真步长。

状态变量迭代求解：

式中i，i+1为迭代次数。是取决于系统状态量和代数量的雅可比矩阵。如式（3）所示，fi如式（4）所示。

其中I为单位矩阵。

3 拓扑结构设计

根据IEC电压等级规定，当发电机容量超过20MW时，应该使用10.6kV的中压发电及配电系统。该船采用四台大容量的发电机组，每台发电机额定功率为20MW，电力容量达80MW。故采用10.6kV中压系统，根据一些负荷需求，低压母线选择380V和220V。对于船舶电力系统，其负荷与运行状态相关，本文仅以巡航状态为例来分析，考虑一定的负荷系数，可以将所有负荷列成表1所示。根据负荷配置表以及辐射形和环形拓扑的特点，最终确定了该船的辐射形和环形两种拓扑如图1和图2所示。

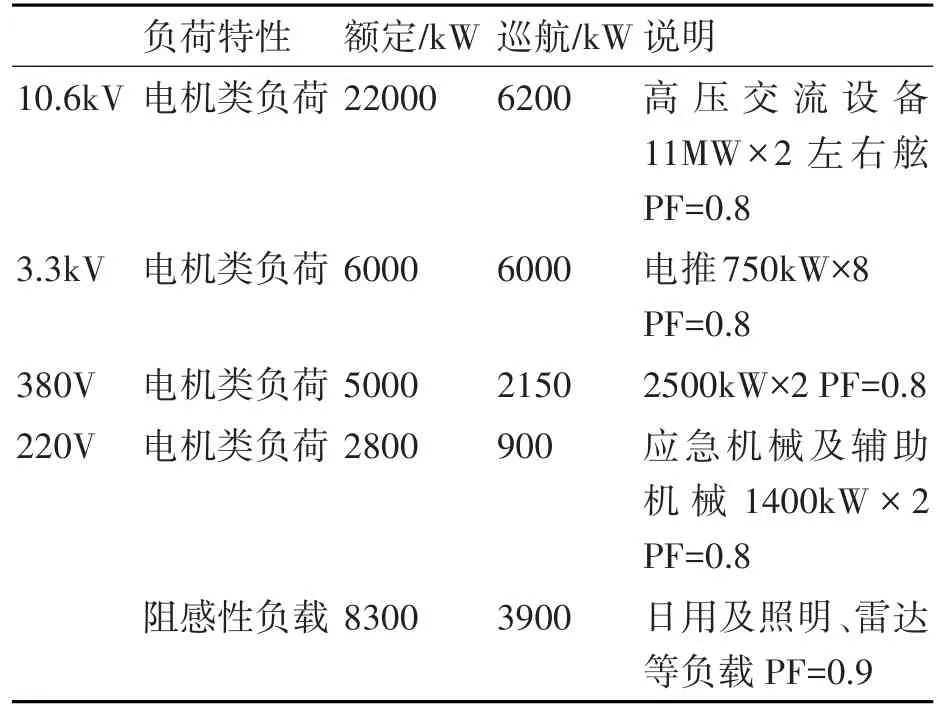
表1 某全电力船舶负荷配置表

图1 辐射形拓扑的船舶电力网络

图2 环形拓扑的船舶电力网络

根据该船的辐射形拓扑和环形拓扑，分别建立其在PSAT平台下的仿真模形。关于PSAT仿真模形的几点说明。

1）仿真中的四台发电机为采用四阶模形，并与自动励磁调节器AVR来配合，稳定机端电压。

2）线路采用π型等值电路，因船上的线路都很短，所以数值较小，损耗可以忽略不计。

3）在原辐射形网络拓扑中，10.6kV的母线只有4根，但是在PSAT软件中，由于软件模块的设定，母线有确定的功率流向，只能从输入端子流向输出端子，为了描述母线之间的功率能够相互流动，加设了几条母线，并用很小的线路阻抗连接，并不影响其功率潮流。

4）经过对辐射形和环形两种拓扑在PSAT中的建模，发现这两种拓扑本质上区别不大，最主要的区别在于环形拓扑在10.6kV母线之间联络母线更多，这也就显现出环形拓扑的一个优势：可以构成更多的电源到负载的通路，所以有更高的供电可靠性。这些分析将在后面的仿真中得到体现。

4 暂态稳定性分析

评估系统受到大扰动之后的指标［3］，一般对于单机系统，用功角随时间变化的曲线作为判断依据；对于多机复杂系统，用各发电机转子之间相对角随时间变化的曲线来衡量。对于本文的系统，就是先给其一个大扰动（投切发负荷或是发生短路故障），然后在通过判断机端电压能否恢复、各发电机转子相对角变化是否能过渡到一个新的平衡点来考量。

4.1 投切大负荷

大容量电机负荷的投入和切除对系统是较大的扰动冲击，通常采用最坏的情况来检验系统的稳定性。基本参数设置：Freq.Base=50Hz，Power.Base=80MVA，Starting Time=0s，Ending Time=50s。发电机G1、G3为平衡节点，发电机G2、G4为PV节点，四台发电机均采用4阶模形并包含励磁调节系统。功率潮流算法选择牛顿拉夫逊算法，时域仿真算法选择前面介绍的隐式梯形法。

首先对辐射形网络进行分析，对母线10.6kV上的大电机类负荷（3.1MW）进行投切仿真，如图3所示，在t=2s时投入3.1MW的大电机类负载，待系统稳定后，在t=25s时切除该负荷。

图3 辐射形网络投切负荷机端电压

发电机1相对于发电机2的转子角如图4所示，可以看到，delta1-2刚开始稳定在0.045rad，在t=2s时，在母线10.6kV上投入大负载电机3.1MW（让电机启动），在经过大约15s，delta1-2稳定在一个新的平衡点0.039rad，这时系统的潮流也达到一个新的平衡点。在t=25s时，将该3.1MW电机负载切除，转子相对角开始变化，在经过大约17s，del⁃ta1-2又重新稳定在0.045rad，回到初始的值，回到初始的功率产生和分配，因此可以得到结论，系统是稳定的。

图4 辐射形网络投切负荷转子相对角

发电机机端电压变化（也即母线10.6kV上的电压变化），在t=2s之后，系统因为母线上突加3.1MW的大负荷，而造成机端电压迅速下降，这时，自动励磁调节系统也迅速跟着起作用（强行励磁装置动作），经过15s的时间，将机端电压振荡地拉回0.99pu。可以看到整个过程，机端电压最大跌落约为6.5%，在10%以内。故可以认为自动励磁调节器有较好的调节行性能，使得系统过渡到一个新的平衡点。在t=25s时，将该3.1MW电机负载切除，机端电压开始上升，系统又经过17s的时间重新回到稳定，也是初始的状态。

接着对环形拓扑进行投切负荷分析，同样的，对母线10.6kV上的大电机类负荷（3.1MW）进行投切仿真，在t=2s时投入3.1MW的大电机类负载，待系统稳定后，在t=25s时切除该负荷。

图5 环形网络投切负荷机端电压

发电机1相对于发电机2的转子角如图6所示，可以看到，delta1-2刚开始稳定在0.022rad，在t=2s时，在母线10.6kV上投入大负载电机3.1MW（让电机启动），在经过大约15s，delta1-2稳定在一个新的平衡点0.030rad，这时系统的潮流也达到一个新的平衡点。在t=25s时，将该3.1MW电机负载切除，转子相对角开始变化，在经过大约17s，del⁃ta1-2又重新稳定在0.022rad，回到初始的值，回到初始的功率产生和分配，故系统是稳定的。

图6 环形网络投切负荷相对转子角

可以看到，无论是辐射形拓扑还是环形拓扑，都能经受住投切大负荷的扰动，在持续大扰动之后能过渡到一个新的平衡状态，且发电机不失步，各发电机仍能保持同步运行，系统是稳定的。

4.2 短路故障

短路故障对于系统则是一个更大的扰动，考虑系统在发生故障后，线路上的保护能迅速动作，经过50ms断路器断开故障支路。设置在时域仿真时间t=5s时，变压器T1出线近母线Bus_k38_2处发生三相短路作为对系统的扰动，经过50ms断开变压器T1所在的线路上的断路器Breaker5以消除故障，不重合该线路。

基本方针参数设置：Freq.Base=50Hz，Power.Base=80MVA，Starting Time=0s，Ending Time=20s。发电机G1、G3为平衡节点，发电机G2、G4为PV节点，四个发电机均采用4阶模形并包含励磁调节系统。功率潮流算法选择牛顿拉夫逊算法，时域仿真算法选择前面介绍的隐式梯形法。

先对辐射形拓扑分析，从图7可以看到，在t=5s前，系统机端电压稳定在额定值，当t=5s，系统发生短路故障，机端电压迅速下跌，考虑到系统整个系统的保护在50ms后动作，机端电压最低值达到0.8pu。在t=1.05s时，在Bus_k38_2和Bus_10k6_7之间的断路器Breaker5断开，系统机端电压开始恢复，大约经过10s的小幅震荡，系统机端电压恢复到标准值。可以看到，这种情况下，系统是暂态稳定的，并且在图8中，发电机转子角变换趋势基本相同，并没有大的失步，可以认为，处于相对稳定状态。

图7 辐射形母线电压波形图

图8 辐射形发电机转子角变化

图9 环形母线电压波形图

在环形拓扑下，在t=5s前，系统机端电压稳定，当t=5s，系统发生短路故障，机端电压迅速下跌，考虑到系统整个系统的保护在50ms后动作，机端电压最低值达到0.998pu。在t=1.05s时，在Bus_k38_2和Bus_10k6_7之间的断路器Breaker5断开，系统机端电压开始恢复，大约经过15s的小幅震荡，系统机端电压恢复到0.9997pu。可以看到，这种情况下，系统是暂态稳定的，并且在图10中，发电机转子角变换趋势基本相同，并没有大的失步，可以认为，处于相对稳定状态。

图10 环形发电机转子角变化

可以看到，辐射形拓扑和环形拓扑都能经受住短路故障扰动，在持续大扰动之后能过渡到新的平衡状态，且发电机不失步，各发电机仍能保持同步运行，系统是稳定的。

5 辐射形和环形拓扑对比分析

通过前面的分析对比，可以知道辐射形和环形拓扑主要区别在于：环形网络在左右舷间联络母线更多一条，设G1和G2在左舷，G3和G4在右舷，环形与辐射形共有一条是G2到G3，比辐射形多一条是G4到G1。如需要观察左右舷联络母线的问题，对于这个稳定裕度较大的系统不适合仿真分析。所以为了观察左右舷的互连，对下面的仿真设置为每台发电机容量为15MW。

系统刚开始运行时，breaker1、breaker2、break⁃er3、breaker4都处于断开状态，系统左右舷同时工作，但在10.6kV和380V母线并没有互连，只是同时给220V负荷供电，在t=10s时，系统在右舷380V母线处发生短路故障，经过50ms，在t=10.05s时，右舷380V母线和10.6kV母线中间的断路器breaker5保护动作。

运行仿真，系统提示出现异常奇点。考察系统特征矩阵，出现负的特征值，系统不稳定，如图11所示。其实这个结果是可以预见的，因为系统发出的左舷发出的功率已经不足以单独提供左舷的全部负荷容量。这时应该让左右舷间的联络线连接起来，让右舷多余的发电容量经过联络线给左舷供电。

图11 在S域实部最大特征值静态稳定性特征值的分析图形

修改仿真环境，在t=10.05s时，联络线间的断路器闭合，对于辐射形，breaker1和breaker2闭合；对于环形，breaker1、breaker2、breaker6和 breaker7闭合，仿真结果如12、图13所示，可以看到，系统在10.05s切除故障后，系统经过一段时间，机端电压能过渡到一个新的平衡状态，系统是暂态稳定的。值得注意的是，辐射形电压跌落到了0.7pu，环形电压跌落只到了0.9978pu。原因在于当G3和G4相邻的10.6kV母线电压跌落后，相比辐射形网络，环形的G1和G2多了一条支路（breaker6支路）给G3和G4来维持机端电压，可以说环形拓扑抗扰动能力更强，稳定性更好。并且环形拓扑在运行时，两条联络线只要有一条能正常工作，就能维持系统的稳定，但辐射形唯一的那根联络线出现断路或者断路器失灵，系统就失步，因此环形拓扑有更强的供电可靠性。

图12 辐射形10.6kV母线电压

图13 环形拓扑10.6kV母线电压

同时，对比图12和图13可以看出，故障后快速切除故障，并且联络母线迅速动作可以有效改善船舶电力系统的暂态稳定性。

6 结语

本文利用PSAT平台来对某全电力船舶拟采用的辐射形和环形拓扑建模和暂态稳定性仿真研究，针对不同的大扰动进行了暂态稳定性的时域仿真，仿真结果显示所设计两种拓扑暂态稳定性良好，并且环形网络稳定性更好，根据仿真结果提出了改善船舶电力系统暂态稳定性的措施。同时结果表明，利用PSAT对电力系统稳定性进行分析，可以得到准确可靠的结果，是进行电力系统建模仿真和稳定性分析的有效工具。