基于应力约束的多相材料结构拓扑优化设计

占金青，彭怡平，龙良明，刘 敏

(华东交通大学 机电与车辆工程学院，江西 南昌 330013)

0 引言

拓扑优化是一种非常有效的结构概念设计方法，通过在指定的载荷作用、边界条件及约束条件下寻求宏观结构或材料微结构的材料最佳布局，从而使其某种性能指标达到最优[1-2]。现有研究大多集中在单一材料结构拓扑优化问题，但由于单一材料结构通常难以实现特定的综合性能要求，且实际工程结构通常由多相材料组成，使得进行多相材料结构拓扑优化设计非常必要[3-4]。

Thomsen等[5]首先进行了多相材料的拓扑优化研究;Sigmund等[6]采用均匀化方法进行负热膨胀系数材料的微结构多相材料拓扑优化设计;Yin等[7]利用峰值函数建立了多相材料拓扑优化设模型;Sigmund[8]提出了基于固体各向同性材惩罚模型的多相材料拓扑优化设计方法;Gao等[9]采用线性对等混合材料插值模型，进行了多相材料结构拓扑优化设计;张宪民等[10]提出了基于平行策略的多相材料拓扑优化设计方法;Zuo等[11]采用序列幂函数插值模型进行了多相材料连续体结构拓扑优化;杜义贤等[12]采用多重网格方法进行多相材料拓扑优化设计，其计算效率有所提高;龙凯等[13]采用独立连续映射方法进行多相材料结构动态拓扑优化设计;Taheri等[14]采用等几何方法进行多相材料的功能梯度结构拓扑优化设计;Zhang等[15]提出了基于基结构法的多相材材料结构非线性拓扑优化设计方法;Liu等[16]进行了考虑尺寸约束的多相材料结构拓扑优化设计研究。目前，多相材料结构拓扑优化研究较多以各相材料体积或质量份数为约束建立拓扑优化模型;但仅以各相材料体积或质量份数为约束的柔度优化获得多相材料拓扑结构难以满足材料失效准则。

目前，应力约束拓扑优化研究主要集中于单一材料结构优化设计。Le等[17]和Holmberg等[18]采用P范数对所有单元的应力凝聚成一个全局应力约束，进行应力约束结构拓扑优化设计;王选等[19]采用改进的双向渐进结构优化法进行应力约束拓扑优化设计研究;占金青等[20]考虑热载荷和机械载荷的共同作用，提出了基于全局应力约束的热弹性结构拓扑优化设计方法;Amir等[21]提出了基于应力约束的弹塑性材料结构拓扑优化设计方法;Collet等[22]采用应力约束进行材料微结构拓扑优化设计;Long等[23]采用二次规划算法进行考虑谐激励作用下的应力约束结构拓扑优化。最近，Guo等[24]通过引入应力梯度函数来避免应力引起的奇异性，采用水平集方法进行多相材料结构局部应力约束拓扑优化设计，并研究以基于应力梯度放大的应力优化列式最小化为目标的多相材料拓扑优化设计方法;Chu等[25-26]采用应力惩罚方法进行多相材料结构应力约束拓扑优化设计，通过应力惩罚项在优化目标中控制结构局部应力，该方法仍属于局部约束，但是避免了大量的单元局部应力约束。

本文提出一种基于可分离应力插值模型的多相材料结构全局应力约束拓扑优化设计方法。采用可分离应力插值模型计算多相材料结构的刚度和应力，以结构体积最小化作为目标函数;采用应力松弛方法来消除应力奇异解现象;利用改进的P范数求解各相材料结构的最大应力，并以各相材料结构的最大应力作为约束，建立多相材料结构全局应力约束拓扑优化模型，进一步采用移动渐近线优化算法进行优化问题求解。

1 多相材料结构全局应力约束拓扑优化模型

1.1 可分离应力插值模型

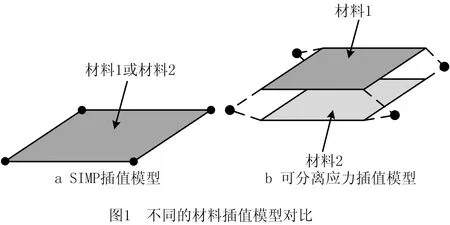
传统的固体各项同性材料惩罚(Solid Isotropic Material with Penalization, SIMP)模型中，每个单元只能对应一个单元刚度和一个单元应力，不能对单独各相材料结构的应力进行计算。采用基于单元堆积方法的可分离应力插值模型[26-27]，在单元应力求解过程中，每个单元能够对应于每相材料都有一个应力，应力的个数与材料的数目有关，如图1所示。多相材结构单元的刚度矩阵可以表示为

(1)

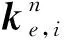
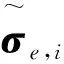
(2)

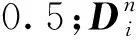
(3)

式中Ei和υi分别为第i相材料的弹性模量和泊松比。

1.2 设计变量过滤方法

连续体结构拓扑优化容易出现网格依赖、棋盘格等现象，采用设计变量过滤能够避免这些数值的不稳定性，获得清晰的拓扑结构[28]。设计变量xe,i通过相邻设计变量xj,i的加权平均，获得对应于第i相材料的过滤单元密度ρe,i。过滤单元密度ρe,i也称为物质密度，用来计算单元的刚度和应力，

(4)

式中：Ωe表示与单元e质心距离小于过滤半径rmin的所有单元集合，如图2所示；wj为权重系数，

(5)

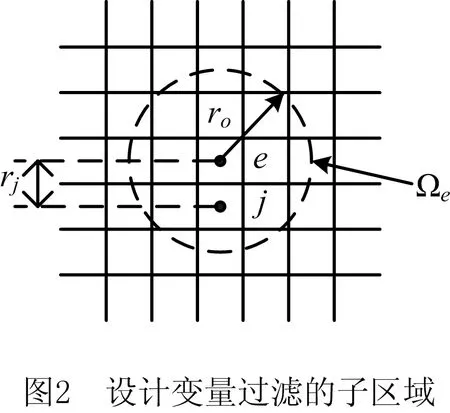
式中：rj为单元j和单元e的质心之间的距离;对于不在子区域Ωe的权重系数wj=0。因此，将单元权重系数wj由原子区域单元扩展至所有单元，设计变量过滤可改写为

(6)

式中:NE为有限元单元的数目;Wej为任一单元的权重系数。

1.3 拓扑优化模型

采用可分离应力插值模型求解结构的单元刚度及应力，以结构的体积最小化作为目标函数，以各相材料的最大应力和其中NM-1相材料的体积作为约束，建立基于应力约束的多相材料结构拓扑优化模型，其拓扑优化模型为

s.t.

KU=F;

(7)

1.4 全局应力约束

单元e对应于第i相材料的Von Mises等效应力可以表示为

=[(σe,i)TVσe,i]1/2。

(8)

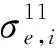
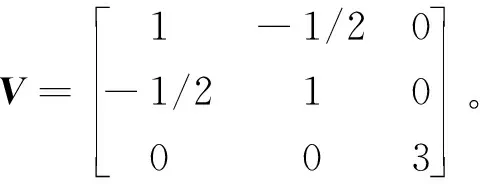
(9)

(10)

对于多相材料结构应力约束拓扑优化问题，结构设计域被离散为NE个单元，每个单元对应多个应力约束，这也意味着约束数目非常巨大，且约束灵敏度分析计算量非常庞大。采用改进的P范数将所有的单元Von Mises应力凝聚化为一个近似等于结构最大Von Mises应力的全局应力，从而大大提高计算效率。第i相材料结构的P范数应力可表示为

(11)

式中P为范数参数。当P趋近无穷大，P范数应力等于最大应力值。但是P不是越大越好，当P越大，非线性越明显，甚至将导致优化问题求解困难，因此P的取值不能太大。文献[17]采用P范数方法，是以单元的体积作为比例因子，具有内置缩放的作用，有利于应力约束优化问题的收敛；但是采用国际单位制时，单元的体积特别小，比例因子内置缩放作用消失。本文以单元密度ρe,i作为比例因子的改进的P范数，采用国际单位制时也能够具有很好的内置缩放作用。

为了使得P范数应力接近最大应力，采用自适应约束缩放方法[20]修改P范数应力：

(12)

式中Ci为自适应约束缩放系数，当迭代步数k≥1时

(13)

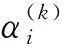
2 灵敏度分析与优化算法

2.1 灵敏度分析

采用基于梯度的优化算法求解应力约束拓扑优化问题，并进行目标函数和约束的灵敏度分析是必要的。

目标函数关于设计变量的灵敏度可直接求导得到：

(14)

对式(12)求导，可得含有第i相材料结构的最大应力约束对单元设计变量xe,i的灵敏度：

(15)

分别对式(15)各项进行求解，则有

(16)

(17)

对式(8)求导有

(18)

式(18)可改写为

(19)

(20)

由于作用载荷恒定，对有限元平衡方程两边同时对单元密度ρe,i求导，则有

(21)

由式(21)可得

(22)

将式(22)代入式(20)，则有

(23)

将式(23)和式(19)代入式(17)有

(24)

令

(25)

将式(24)和式(16)代入式(15)，则有

(26)

令有下列伴随方程

(27)

由式(27)求出λe，式(26)可改写为

(28)

其中

(29)

2.2 优化算法

连续体结构拓扑优化问题通常主要采用优化准则算法(Optimality Criteria method, OC)和数学规划算法求解。OC算法[29]简单明了，但是难以适用于多约束的多相材料结构应力约束拓扑优化问题。移动渐近优化算法(Method of Moving Asymptotes，MMA)[30]适用于复杂的多约束优化问题求解，具有很好的鲁棒性。本文采用MMA算法进行多相材料结构应力约束拓扑优化问题求解。

3 数值算例

本章中，多相材料结构应力约束拓扑优化设计方法在MATLAB软件中编程实现，通过两个数值算例来验证其有效性。所有算例中，实体材料1和实体材料2的弹性模量分别为190 GPa和210 GPa，泊松比μ均为0.3，两相材料的屈服应力极限值分别为σ1=241 MPa和σ2=358 MPa。设计变量过滤的半径rmin=2.5，范数参数P=8。

3.1 L型梁结构

L型梁结构的设计域、作用载荷及边界条件如图3所示。L型梁结构尺寸为100 mm×100 mm，厚度为1 mm，固定梁结构的左上端，施加作用荷载F大小为250 N，均匀分布在结构右上端的6节点上，如图3的局部放大所显示，以避免载荷作用区域应力集中。材料2的体积份数约束β2=0.15，初始结构域离散成6 400个四节点平面应力单元。

为验证所提方法的有效性，对L型梁进行有、无应力约束多相材料结构拓扑优化设计。无应力约束多相材料结构拓扑优化采用体积约束的结构柔度最小化模型，各相材料体积份数约束的大小根据应力约束拓扑优化结果得到，其他设计参数与应力约束多相材料结构拓扑优化相同。有无应力约束多相材料结构拓扑优化的L型梁结构的拓扑图及应力分布图分别如图4和图5所示。拓扑结构中红色区域代表实体材料1(弹性模量小)，蓝色区域代表实体材料2(弹性模量大)，白色区域代表空洞。

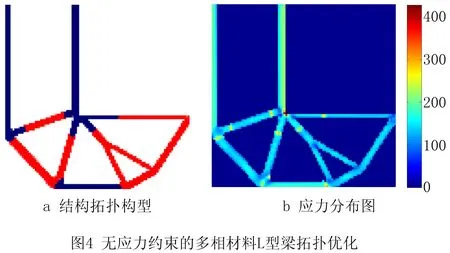
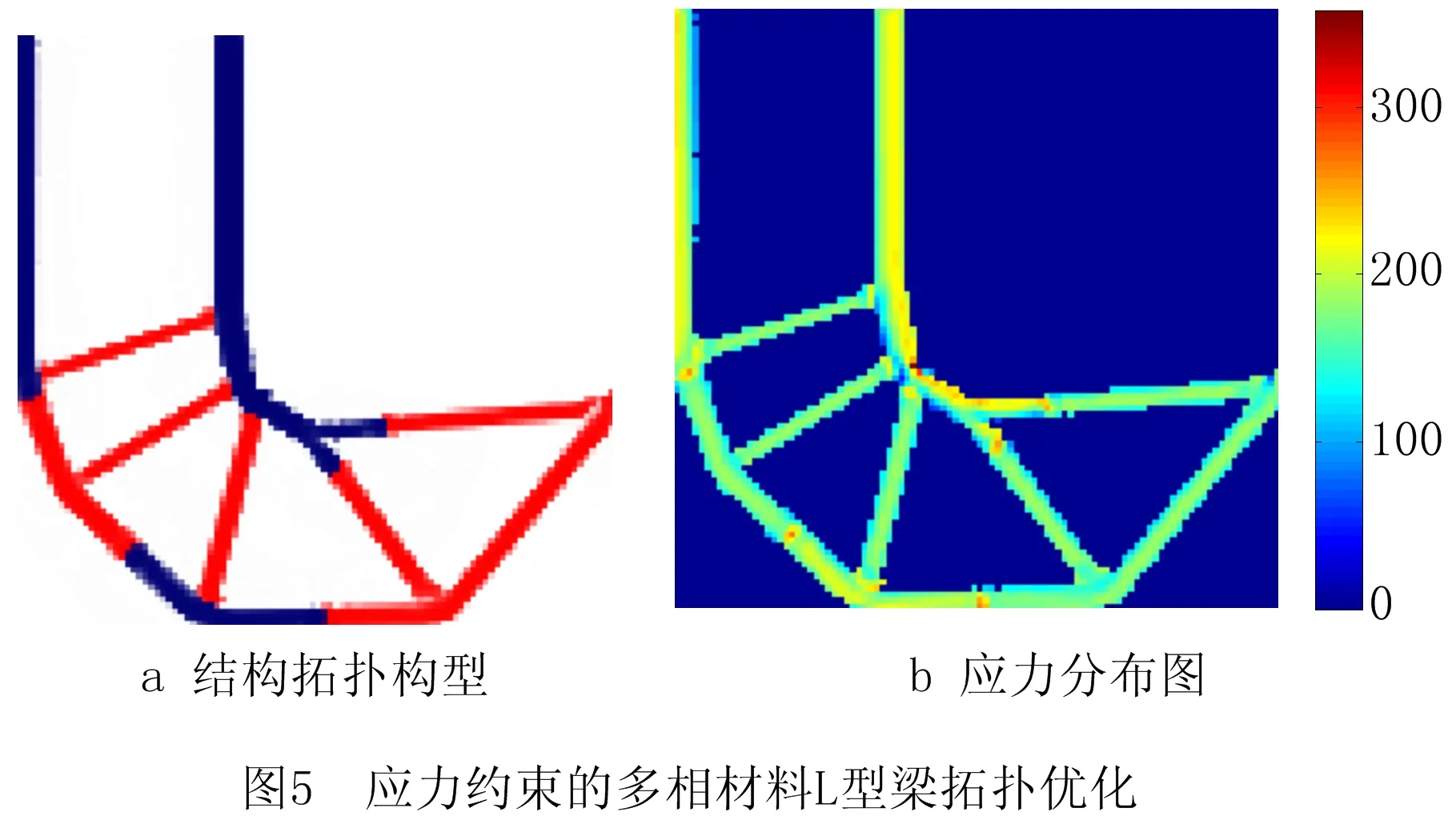
由图4和表1可知，无应力约束多相材料结构拓扑优化获得的L型梁拓扑结构位于内凹角拐角出现明显应力集现象，材料1和材料2结构的最大应力分别为305.719 MPa和428.738 MPa，均超过材料1和材料2的屈服极限值。然而，应力约束多相材料结构拓扑优化获得的拓扑结构在拐角处出现了过渡弧形边界(如图5)，并且结构的应力分布更加均匀，有效地抑制了应力集中现象。由图4b和图5b可见，有些不同相材料连接区域存在应力不连续现象，这主要是位于不同相材料连接区域出现两种相材料堆积的单元，且存在两材料堆积的单元在应力分布图中只显示应力较大的相材料应力分布，从而导致有些不同材料连接区域存在应力不连续现象。由表1可知，在应力约束拓扑优化获得拓扑结构中，材料1结构和材料2结构的最大应力分别240.669 MPa和358.008 MPa，均能很好地满足应力约束极限值，满足结构的静强度要求；与无应力约束拓扑优化相比，应力约束多相材料拓扑优化获得L型梁结构的柔度较大，但是其拓扑结构的强度更好，结构应力分布更加均匀。

表1 不同优化模型获得的L梁拓扑优化结果

3.2 悬臂梁结构

悬臂梁结构的设计域、作用载荷及边界条件如图6所示。悬臂梁结构尺寸为200 mm×100 mm，厚度为1 mm；结构的左端固定，均布载荷施加结构的右端中部，载荷的大小为800 N，均匀分布5单元节点上。材料2的体积份数约束β2=0.25。初始结构域离散成20 000个四节点平面应力单元。

有无应力约束多相材料结构拓扑优化的悬臂型梁结构拓扑图及应力分布图分别如图7和图8所示。同样，由图7和表2可知，无应力约束多相材料结构拓扑优化获得的悬臂梁拓扑结构中，材料1和材料2结构的最大应力分别为306.312 MPa和490.421 MPa，也均超过材料1和材料2的屈服极限值。然而，应力约束多相材料结构拓扑优化获得的悬臂梁拓扑结构有很大不同，边界形状突变得到抑制(如图8)，且结构的应力分布更加均匀，有效地抑制了应力集中现象。由表2可知，在应力约束拓扑优化获得优化结构中，材料1结构和材料2结构的最大应力分别为240.719 MPa和345.430 MPa，均没有超过材料屈服极限值，满足结构的静强度要求。同样，与无应力约束拓扑优化相比，应力约束多相材料拓扑优化获得优悬臂梁结构的柔度较大，但是其拓扑结构的强度更好，结构应力分布更加均匀。

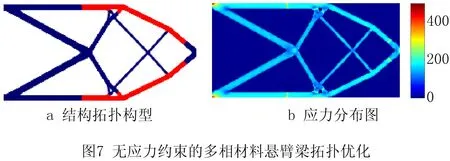
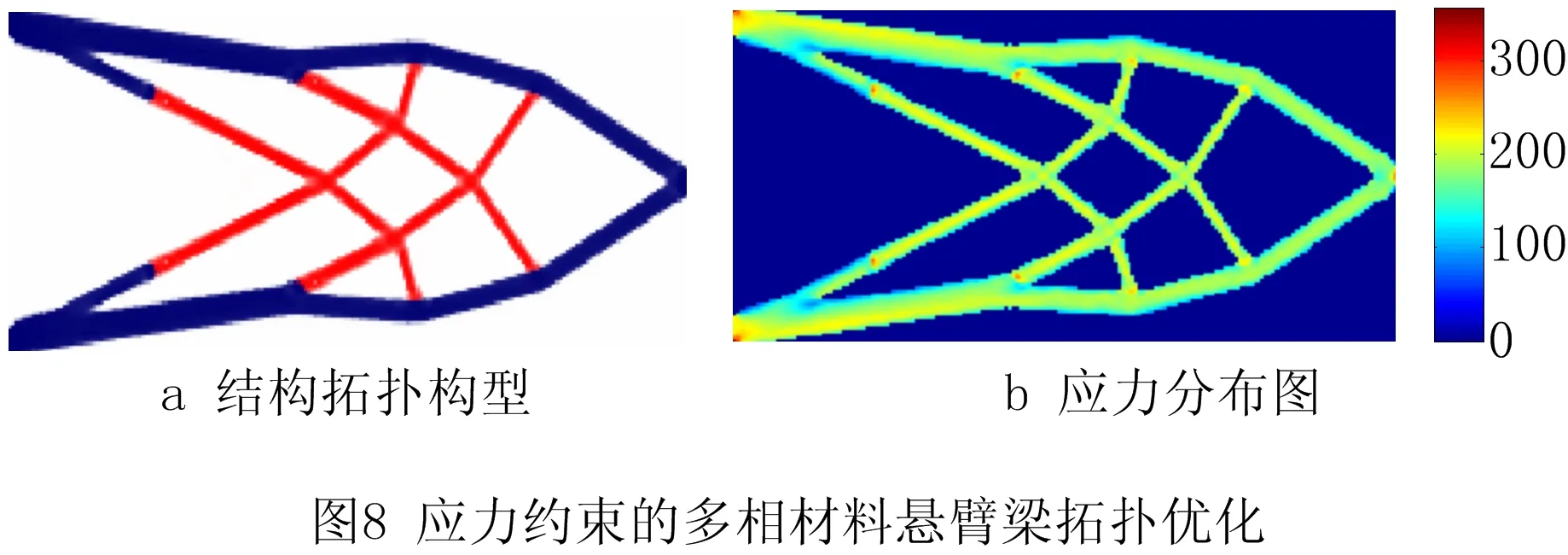
表2 不同优化模型获得的悬臂梁拓扑优化结果

4 结束语

本文基于可分离应力插值模型提出了多相材料结构全局应力约束拓扑优化设计方法。以结构体积最小化作为目标函数，将可分离应力插值模型用于计算多相材料结构的刚度和应力，实现计算每相材料结构的应力，采用改进的P范数求解结构的最大应力，并以各相材料结构的最大应力作为约束，建立了多相材料结构全局应力约束拓扑优化模型，进行优化问题求解，通过数值算例验证了其可行性。

算例结果表明，与无应力约束比较，应力约束的多相材料结构拓扑优化获得的拓扑结构有所不同，能很好地满足各相材料应力约束，满足强度失效准则；能够抑制应力集中现象，使得多相材料结构应力分布更加均匀。本文是在确定性载荷条件下进行的研究工作，未来将考虑载荷不确定性因素对多相材料结构应力约束拓扑优化结果的影响。