基于双维度EKNN的滚动轴承早期故障分类算法
2021-02-25唐朝晖桂卫华
彭 成,贺 婧,唐朝晖,陈 青,桂卫华
(1.湖南工业大学 计算机学院,湖南 株洲 412007;2.中南大学 自动化学院,湖南 长沙 410083)
0 引言
滚动轴承[1]是旋转机械装置的关键组成部分,其性能的好坏直接影响整个设备的运行状态。在故障发生的早期,故障缺陷如裂纹尺寸等相对较小,特征过于微弱,难以及时检测并定位。而当早期故障扩展到一定程度时,将影响旋转机械装置的正常运行和整体效能,甚至导致灾难性事故的发生。若能采集早期故障的信号数据[2],并实时提取最能表征轴承运行状态的特征信息,精确地对早期故障进行识别诊断,便可以及早规避风险,优化维修策略,降低成本支出。因此,对滚动轴承进行早期检测和故障诊断意义重大。
目前,滚动轴承故障诊断可分为3个步骤,分别为特征提取、特征选择和故障识别[3]。振动信号分析是轴承故障特征提取和诊断的常用方法[4]。Wang等[5]、Cheng等[6]采用收集成本低且具有简便性的电流和振动信号进行故障诊断,但其局限性在于无法对轴承早期所激发的微弱故障进行特征提取和精确诊断。声发射(Acoustic Emission, AE)是一种新型在线无损检测技术,在物体产生变形、裂纹等缺陷的初始阶段就能接收到大量的AE信号,且AE信号的频率范围一般在100 kHz~1 000 kHz之间,不受其他噪音影响[7-9]。因此,AE技术在早期轴承故障诊断方面具有更高的敏感性和可靠性。Sánchez等[10]通过提取振动、电流和AE信号中的特征按Chi排序使用K最近邻(K Nearest Neighbor, KNN)分类器对早期故障进行诊断,实验结果表明由于AE信号具有频谱宽、抗干扰性强和故障特征明显的特点,AE信号在早期故障诊断中精确度达到96%,高出振动信号2个百分点; Chanamala等[11]主要研究了AE技术在不同转速、负载条件下对轴承外圈裂纹的早期故障识别,实验结果表明AE技术不仅能有效地检测出早期故障,还能监测裂纹的产生和扩展过程;Mary等[12-13]进一步研究表明,将AE信号的参数与六个时域特征结合分析,不但可以判断出外圈裂纹故障的尺寸大小,还可以通过特征值的变化对裂纹尺寸大小的变化进行预测,而振动检测技术却无法实现;Elforjani等[14]在实验中发现均方根值和AE信号振幅随时间的分布情况可预测轴承故障的发展趋势从而较为精确地识别早期缺陷的类别。
AE技术为轴承早期故障的诊断奠定了基础,但上述文献缺少对AE信号进行多工况、多部位的特征提取。因此,本文构建波形、时域和频域混合特征池来充分表征轴承的早期故障特点。然而,剔除混合特征池中对反映故障特点贡献不大的冗余特征以及相关性较大的特征,保留具有显著类别差异的信息特征是一大难点。Lu等[15]提出一种基于遗传算法和动态搜索策略的优势特征选择方法,用于寻找轴承故障诊断中最具代表性的特征。遗传算法可以实现较高质量的特征选择,但在计算时间方面的代价过高且容易陷入局部最优。相比之下,序列前向选择算法(Sequential Forward Selection, SFS)的运行速度相对较快,能够很好地平衡计算时间和所选最优特征的质量。Islam等[16]、Ding等[17]使用属性值、评估模型来创建特征向量、特征子集的目标等级值,并基于SFS算法对特征的目标等级值排序从而进行特征选择;Kang等[18]开发了一种基于SFS的异常值不敏感的混合特征选择(Outlier-Insensitive Hybrid Feature Selection, OIHFS)方法来评估特征子集质量,创建新的特征评估指标,通过识别各工况下正常和有缺陷的滚动轴承,验证了该方法的有效性;Homsapaya等[19]提出一种基于SFS的类内和类间距离特征子集评估方法,类间距离通过计算两两之间的欧式距离得到。本文在上述文献仅考虑类内稠密区样本分布的基础上,同时考虑类内类间样本的全局分布,关注位于较不密集区域或类外围的样本,在优化判别目标函数的同时引入反馈停止策略和早弃策略,使得选择的特征组更精简,更能表征早期故障特性。
在早期故障识别方面,陈法法等[20]针对滚动轴承早期故障特征微弱、难以快速有效辨识的问题,构造了一种基于正交邻域保持嵌入与多核相关向量机的机器学习模型;Jia等[21]结合K-means分类器和t-分布领域嵌入算法(t-Distributed Stochastic Neighbor Embedding, t-SNE)提出一种从大量振动信号中自动提取特征的方法;Bugata等[22]提出一种基于距离和属性加权KNN的新型监督特征选择方法(Weighted KNN-Feature Selection, WKNN-FS);Aguilera等[23]使用类内(Circled by its own Class, CC)和类间(Circled by Dierent classes, CD)对训练对象进行质量分配的方法,提出一种基于物体间引力的加权KNN算法(Weighted Attraction Force KNN, WAF-KNN);Sharma等[24]采用平方反特征加权技术,提出了一种使用加权K最近邻分类器(Weighted KNN, WKNN)进行轴承故障诊断的新方法,实现了故障的100%高精度检测。这些研究成果为特征选择算法结合分类器在滚动轴承早期故障诊断中的应用开辟了新的思路,但均没有系统地研究K值对特征提取结果的影响。Domingues等[25]提出了基于局部异常因子(Local Outlier Factor, LOF)的离群点检测方法;杜旭升等[26]提出基于领域系统密度差异度量的离群点检测(Neighborhood System Density Difference, NSD)方法。这些方法在距离度量基础上,加入密度度量[27],提高了算法鲁棒性,为离群点的检测提供了新的技术借鉴,但当数据集较大、系统内部结构复杂时,计算近邻可达密度会产生较大的偏差。
本文针对早期故障信号特征之间的相关性和冗余对故障分类计算复杂性和精确度的干扰、传统的KNN分类器直接采用距离计算进行分类的能力不足、对K值敏感性较大而不利于早期故障分类等问题,以低转速下的滚动轴承早期故障为研究对象,通过提取AE信号的波形特征、时域和频域的统计特征构造混合特征集,采用隶属度矩阵计算类内紧致性和类间重叠性参数,并将二者的比值作为SFS算法进行特征选择的目标函数,这种新方法能对冗余特征进行压缩,减少特征相关性对分类的影响;同时提出反馈停止策略和早弃策略,提高算法效率。最后,将一种新的密度计算方法用于传统KNN分类器,采用密度和距离双维度计算的EKNN分类器降低对K值的敏感性,更稳定地识别出最优特征组,实验结果验证了本文所提方法的有效性和准确性。
1 混合特征提取
AE无损检测技术是一种非常有前景的动态非破坏检测技术,能够提高对滚动轴承早期故障状态的诊断性能,可以为大量基于数据驱动的故障诊断方法提供基础信息,但AE信号具有非平稳性、复杂性和多样性等特点[28],从中直接获取故障状态的内在信息非常困难,且单一的特征对故障初始阶段的敏感性低。为此,采用波形特征参数法和波形分析法对AE信号进行特征提取,同时从时域和频域提取特征,从而构造混合特征池,对滚动轴承的早期故障特征进行量化,全面反映早期故障的敏感特征。
本文的高维混合特征向量由AE故障信号中提取的21个特征组成,包括采用波形特征参数法提取的5个波形特征、采用波形分析法提取的10个时域和6个频域特征。波形特征包括上升时间(f1)、计数(f2)、持续时间(f3)、幅度(f4)和能量(f5);时域统计特征包括均值(f6)、均方根值(f7)、峰值(f8)、方根幅值(f9)、峭度(f10)、峭度因子(f11)、波形因子(f12)、裕度因子(f13)、峰值因子(f14)、脉冲因子(f15);频域统计特征包括功率谱方差(f16)、相关因子(f17)、谐波因子(f18)、谱原点矩(f19)、重心指标(f20)和均方频谱(f21)。如表1所示为所有时域和频域统计特征的公式定义[29]。因为每个特征参数是用不同统计方法计算的,会对本文算法产生一定影响,所以将各个特征参数转换到[0,1]范围中,称为最大最小归一化[30],即
(1)
式中:xmax为样本数据的最大值;xmin为样本数据的最小值。

表1 统计特征公式定义
2 特征选择
一般地,早期故障分类方法获取不同类型的故障数据构造的高维混合特征中存在彼此相关性大、冗余的特征,导致计算复杂度增加、计算成本上升[31-32]。因此,如何使用特征选择算法压缩冗余,筛选出最优早期故障特征对提高故障分类性能十分重要。
序列前向选择算法(SFS)通常用于特征选择中,是一种自下而上的贪婪搜索方法[33]。虽然SFS算法简单、高效且较准确,但也存在缺点,其中最明显的是仅根据人为经验来设置使算法停止的最大维数值,即当目标特征子集的特征维数达到预先设定最大维数时停止运算。为此,本文对SFS算法进行改进,以隶属度矩阵计算类内紧致性和类间重叠性的比值作为目标函数,将使得目标函数值最大的特征作为EKNN分类器的输入,同时改进的SFS算法根据反馈结果决定是否继续搜索,提早丢弃目标函数值最小的特征,提高了处理效率。改进的SFS算法的相关定义如下。
2.1 相关定义
定义1隶属度矩阵。
(2)
式中:dip为第i个样本与第p个类别的欧式距离;diq为第i个样本与第q个类别的欧式距离;c为故障类别个数;s为模糊因子,用来决定模糊度的权重指数。
定义2类内紧致度。
(3)
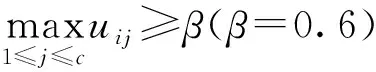
定义3类间重叠性。
(4)
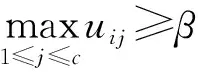
定义4目标函数。目标函数为类内紧致度与类间重叠性的比值,即
(5)
不难发现,类内紧致性越大,Compact(c,U)值越大,类间重叠性越小,Overlap(c,U)值越小,可得V值越大,筛选结果越好。
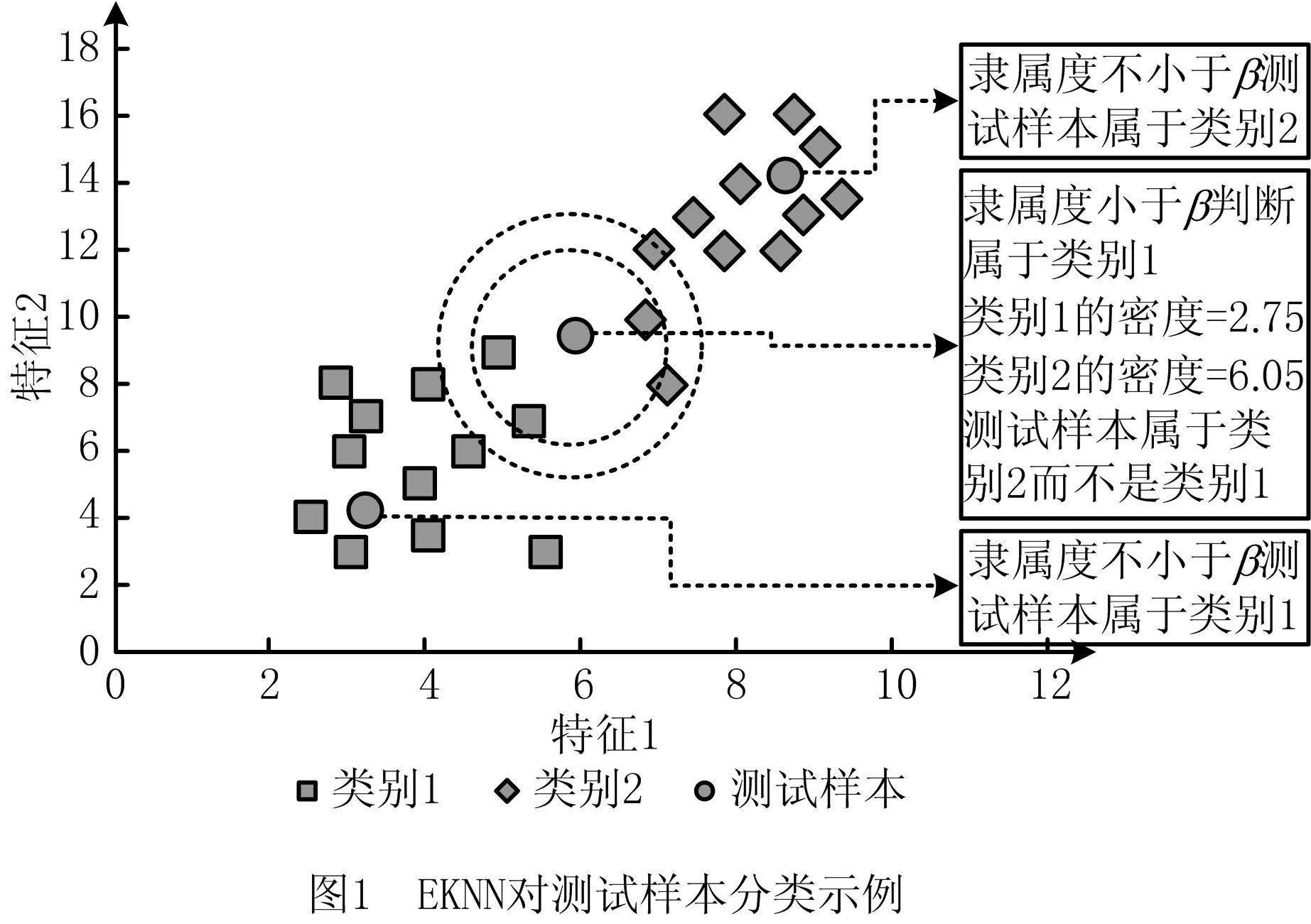
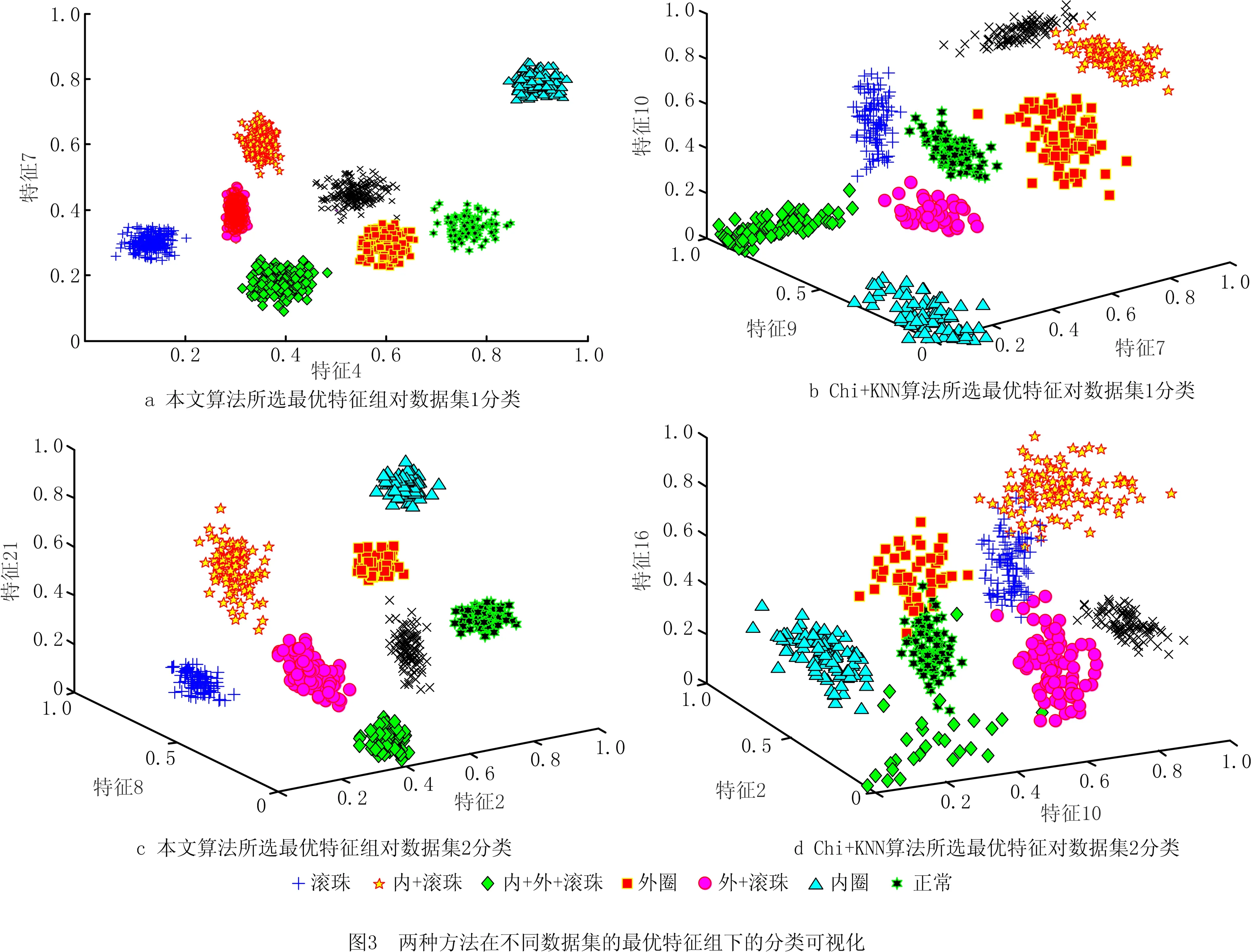
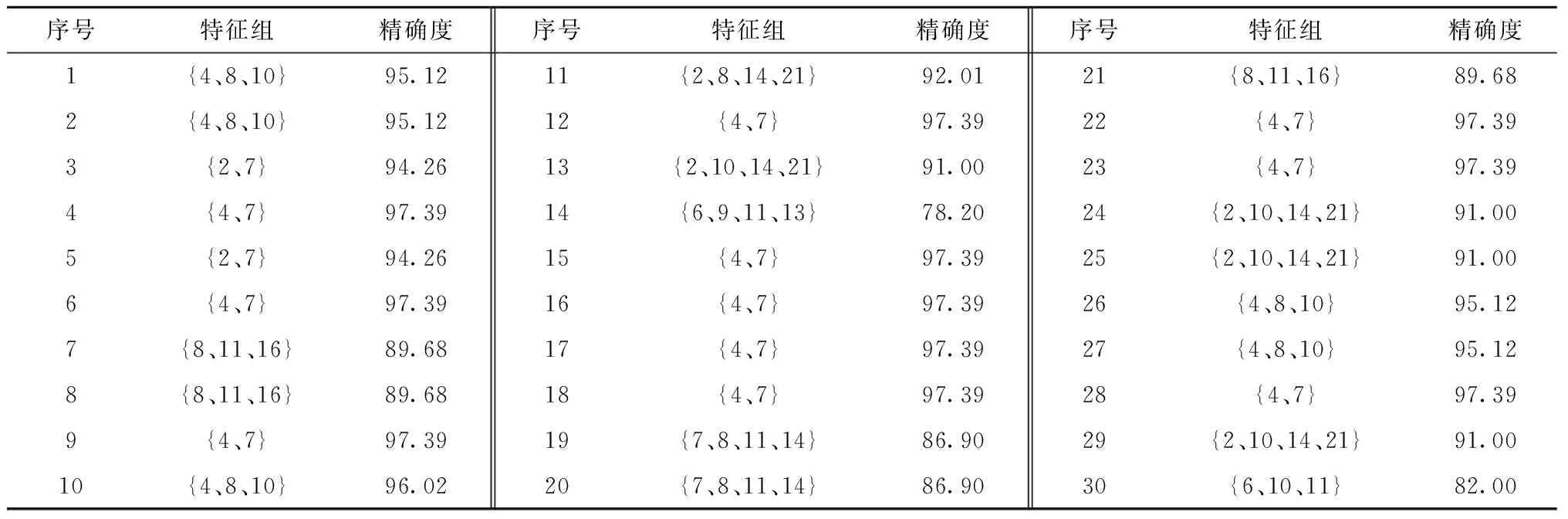
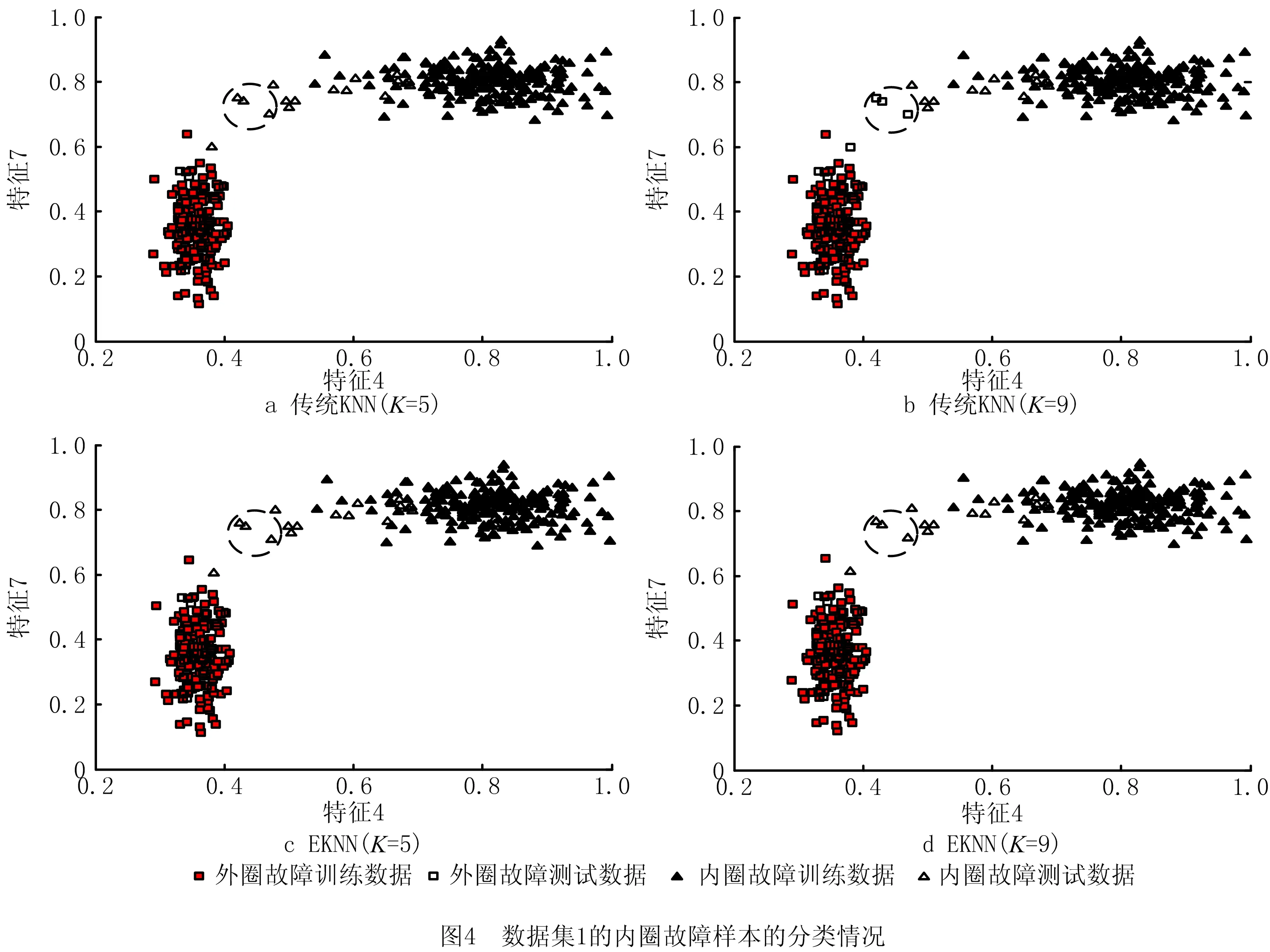
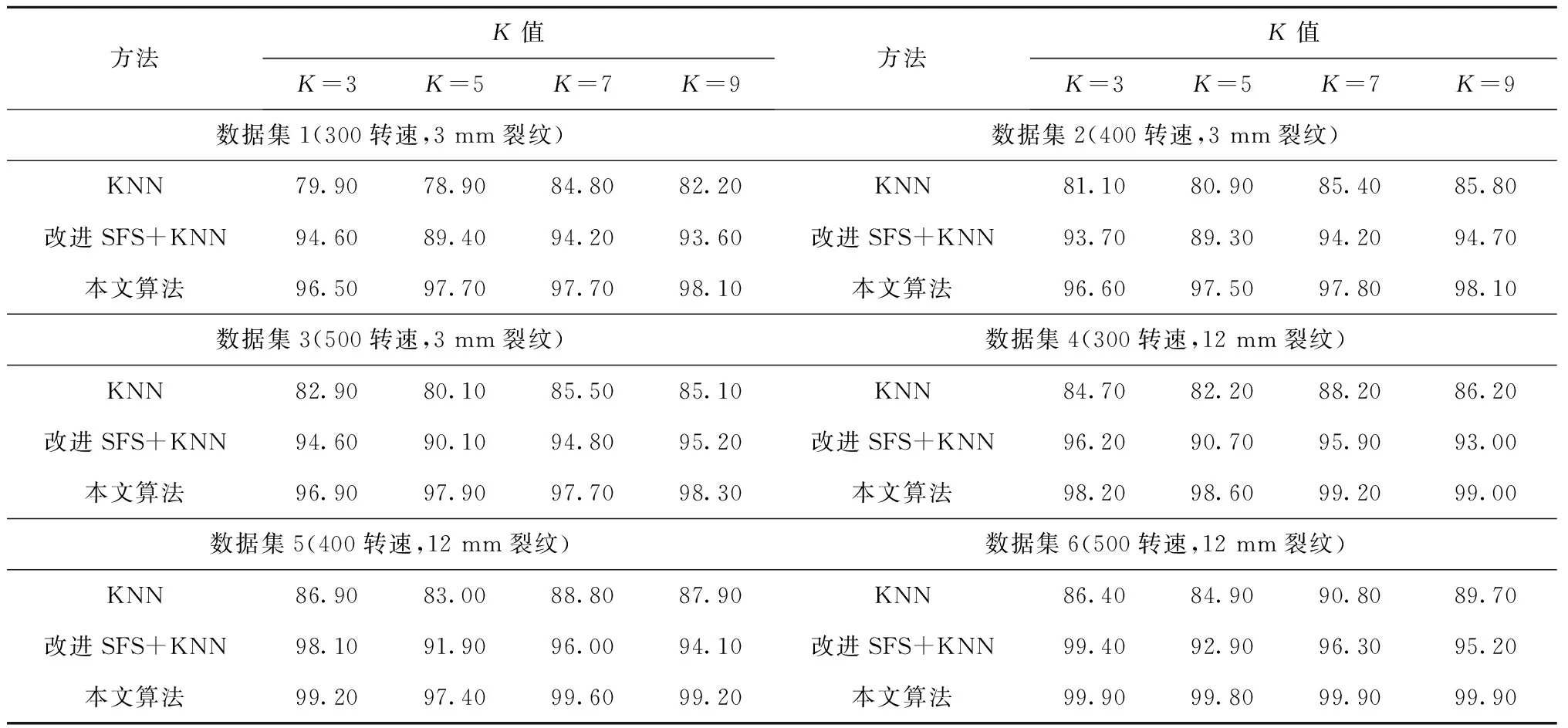
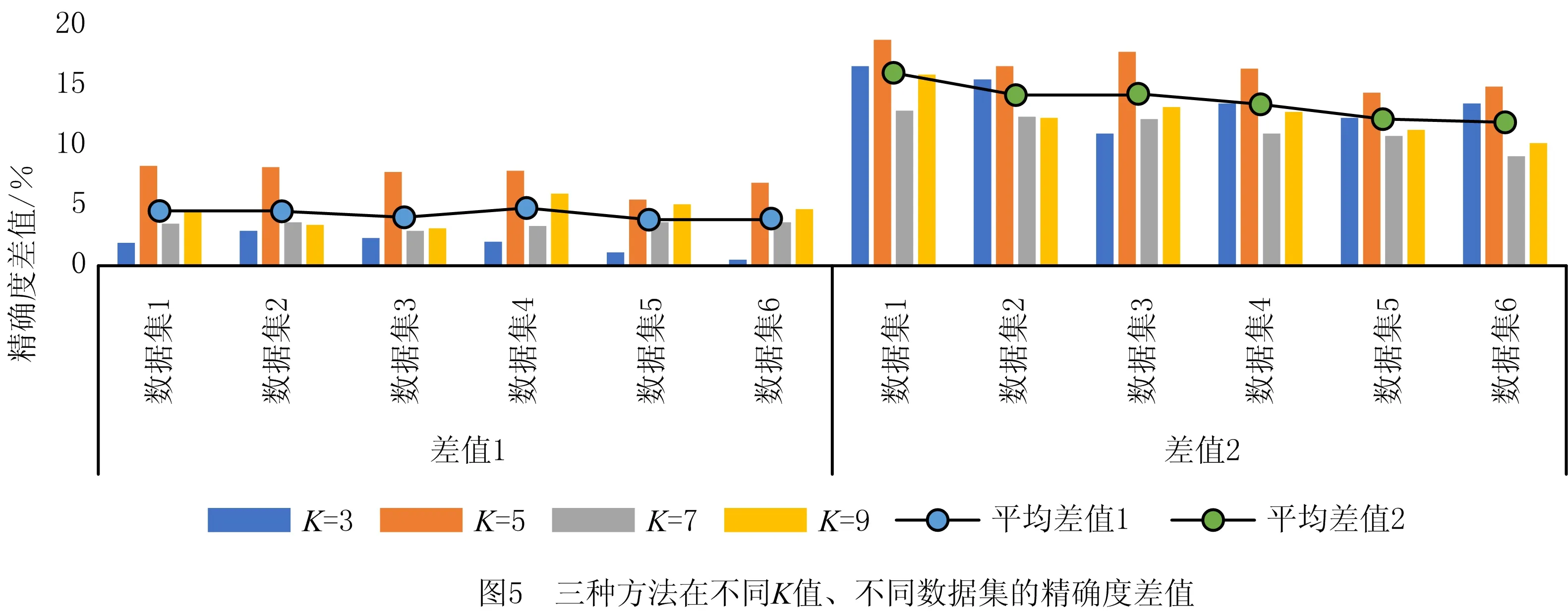
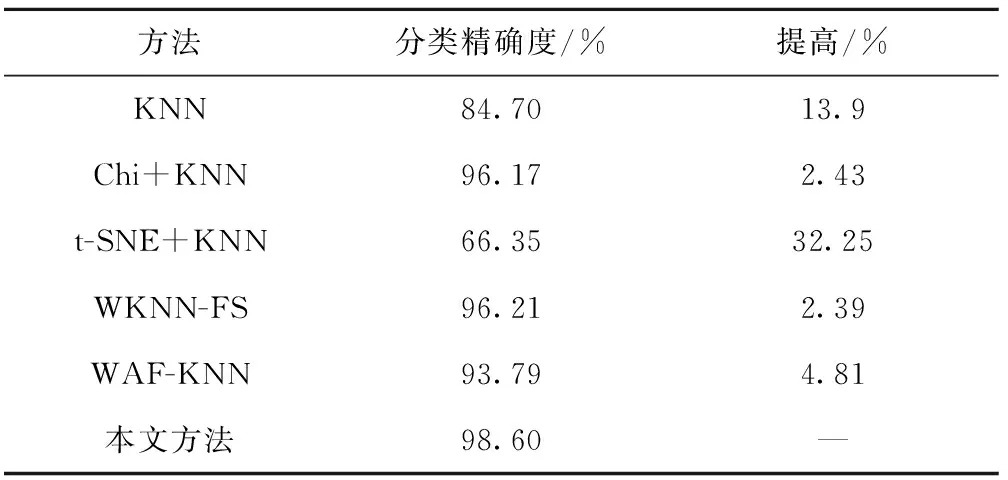
定义5反馈停止策略。将每一次更新后的目标特征集FF={FF1,FF2,…,FFn}送入EKNN分类器计算后会产生对应的分类精确度pre={pre1,pre2,…,prer},若max{|prer+1-prer|,|prer+2-prer+1}<θ且满足prer 定义6提早丢弃策略。计算原始特征集F=(f1,f2,…,f21)中每一个特征的目标函数评价值V(fi),丢弃最小函数值V(fi)=min{V(fi)}的特征,对更新后的组合特征,重复上述操作。 算法1改进的SFS算法。 1.Input目标特征集FF={∅},原始特征集F=(f1,f2,…,fn),特征数n=0,精确度阈值θ 2.计算F中每个特征V值,V=compact(F)∕overlap(F) 8.重复步骤3~步骤6 9.计算每次更新后的FF由EKNN分类器得到的精确度 10.循环以上步骤直到满足精确度差值小于阈值θ,即Untilmax{|prer+1-prer|,|prer+2-prer+1}<θ且满足prer 11.Output FF 改进SFS算法的时间复杂度由于采用了早弃策略,能够提前停止搜索,相较于原始SFS算法未采用早弃策略能节省运算时间、提高效率。改进的SFS算法第一次选择特征加入目标特征集时,计算n个特征的目标函数值;第二次选择时,计算(n-2)个函数值;第s次选择时,计算(n-2s+2)个函数值。当目标特征集最终的个数为m时,需要计算(n-m+1)×m个目标函数值,因此改进SFS算法的时间复杂度为O((n-m+1)×m)。 KNN是一种简单且有效的分类器,传统KNN分类器的核心思想是使用距离计算来确定最近邻居,根据训练集中的大多数最近邻居来标记未知的测试样本[34]。但在早期故障中,正常样本和异常值会出现紧密重叠部分,KNN分类器难以识别,将导致分类精确度显著下降,同时非常容易受到邻域K值大小的影响。本文在传统KNN仅使用基于距离度量方法上,考虑各数据样本的密度,提出一种新的基于距离和密度双维度计算的EKNN分类器,在计算时既考虑数据集的全局特征,也考虑局部密度特点,能够对早期故障进行更精确的识别和分类。EKNN相关定义如下。 定义1欧式距离。 (6) 式中:xi={xi1,xi2,…,xim}为某两个特征中的数据点;NK(xi)为xi的K个近邻。距离值升序排列表述为: KNN(xi)={j∈X|d(xi,xj)≤d(xi, NK(xi))}。 (7) 定义2密度计算。利用密度函数计算样本xi的局部密度,再计算样本xi与其近邻距离的最小值δi。 (8) (9) 最后得出测试样本xi的输出概率值Pi=ρi/δi,标记测试样本为Pi值对应的类别。式(8)用KNN(xi)来计算xi的局部密度,其中ρi值越大,表示xi的局部密度越大;用式(9)计算每个样本的δi值,其中δi值越小,表示xi距离某个类别越近。根据Pi=ρi/δi得到xi到各类别的Pi值,按降序排列,将xi归入Pi值最大的类别。 对于给定的测试样本,EKNN分类方法首先计算测试样本关于不同类别的隶属度,再根据隶属度作进一步操作,若隶属度不小于β,认为该测试样本的所有最近邻居都属于某个确定的类别,则标记测试样本为此单个类别;若隶属度小于β,则使用基于距离和密度双维度计算方法来确定测试样本的标签,即根据上述定义得出测试样本的(ρi,δi)值和相应的Pi值,标记测试样本为Pi值大对应的类别。如图1所示,给定的3个测试样本中有两个测试样本可以十分确定地通过隶属度计算出故障类别,分别属于类别1与类别2;中间的测试样本,当K=3时,属于类别1,当K=5时,属于类别2,而隶属度计算出的类别为类别1,与实际结果并不符合,使用密度度量来确定测试样本的最终类别,结果为类别2,符合实际结果。算法描述如算法2所示。 算法2EKNN分类算法。 1.Input数据集,算法1所得目标特征集,隶属度矩阵 2.if样本隶属度≥β then 3.即所有最近邻居都属于某个确定的类别,标记样本属于此类别 4.else 5.样本处于重叠区域,使用距离和密度双维度计算的EKNN分类 6.计算欧式距离,d(i,j)=d(xi,xj) 7.对欧式距离排序,KNN(xi)=sort(d(i,j)) 8.样本基于式(8)和式(9)计算ρi,δi 9.Pi=ρi/δi得到样本的最终密度值 10.sort(Pi)对密度值排序 11.max(Pi)为样本所在类别 12.End if 13.Output分类结果 基于一种新的密度和距离双维度计算的EKNN算法,原理简单且时间复杂度低。其中,计算数据集中数据对象之间的距离矩阵所需时间复杂度为O(n2),基于二分思想进行排序的时间复杂度为O(nlog2n),而计算局部密度ρi和KNN距离δi所需的时间复杂度均为(n2),计算样本所属的标签可在O(n2)的时间复杂度内完成,故EKNN算法的时间复杂度为O(n2)。传统KNN存在向量的维度越高,对距离的区分能力越弱的缺点,其时间复杂度为O(tkmn),其中:t为迭代次数,k为簇的数目,m为记录数,n为维数。 本次滚动轴承早期故障诊断实验使用滚动轴承传动系统试验台,该平台由调压器、驱动电动机、滚动轴承安装架、传感器、加速计和数据采集系统等部分构成。实验的滚动轴承型号为6 308,滚珠为8个,钢球直径为15 mm,滚道节径为65.5 mm,轴承的内径为40 mm,轴承外径为90 mm。AE采集系统由型号为R15,频率为70~150 kHz的宽频AE传感器、带有2通道的PCI-2声发射数据采集卡、型号为1220A系列,增益指标为40 dB的前置放大器及同轴电缆组成。在试验台上分别安装完好的轴承、包含人为制造的3 mm裂纹来模拟早期故障的轴承及12 mm裂纹的轴承。此外,分别在300、400和500转速下采集正常、内圈故障、外圈故障、滚珠故障、内圈与外圈故障、内圈与滚珠故障、外圈与滚珠故障、和内圈、外圈与滚珠故障下的8个类别的AE信号,数据集属性如表2所示。对于每种轴承故障,记录200个AE信号,每个信号持续10秒,同样,健康轴承数据记录200个AE信号。因此,总共有6个数据集,每个数据集总共包含1 600个AE信号。 表2 数据集属性 为验证本算法的真实有效性,本文采用k-fold交叉验证方法,通过平均k个不同分组训练结果来减少偏差,有效地避免过学习以及欠学习状态的发生。通常,k的取值一般大于等于2,在原始数据集合数据量小时,k的取值为2。为了抵消数据维度增加的计算成本,同时由于实验的有效性更依赖于数据集中变量的个数而不是分组训练的偏差[35],因此本文选取k值为3。本文在早期微弱特征选择过程中构建的高维特征样本池的维数为Nf×Ns×Nc,其中特征的数量Nf为21个,每个数据集的样本数量Ns为200个,类别数量Nc为8个。如图2所示,使用MATLAB中的randperm函数将高维特征池中的样本随机被分成3份,经过N次交叉验证(N=10)后,得出最优特征组,共包含N×k个候选次优特征组。 实验1改进的SFS+EKNN算法性能分析。 如前所述,采用的混合特征集合包含3个不同域的21种特征:波形特征5个(f1-f5)、时域统计特征10个(f6-f15)、频域统计特征6个(f16-f21)。为验证本文算法的有效性,与文献[10]提出的Chi+KNN算法进行比较,Chi+KNN算法通过提取振动、电流和AE信号中的特征,并将其按Chi排序输入KNN实现早期故障诊断,与本文提出的实施过程相似,具有可比性。如表3所示,本文采用改进的SFS+EKNN算法和Chi+KNN算法对6个数据集进行特征选择,得到不同的最优特征组,且最优特征组中特征个数更精简,精确度却更高。精确度反映了被判定的正例中真正的正例样本的比重,公式定义如下: (10) 表3 不同数据集的最优特征组 式中:Nt为分类正确的正例样本数;Nc为类别数;Nsc为第c个类别的样本总数。 根据表3,本文算法在不同数据集下的精确度均比Chi+KNN算法高,在数据集4~数据集6中平均精确度高出1.74%。特别地,在早期故障数据集1~数据集3中平均精确度高出Chi+KNN算法2.98%。早期故障数据集1~数据集3的精确度在Chi+KNN算法的基础上分别提高了1.98%、4.57% 和2.39%,且等于甚至超过在数据集4~数据集6上的增幅。本文算法在早期故障数据集1~数据集3的平均精确度仅低于数据集4~数据集6的1.71%,而Chi+KNN算法低于2.95%。因此,本文算法对轴承的早期故障诊断具有适用性和有效性。由于受特征与特征之间的相关性、类别与特征之间的关联度等因素影响,算法对于不同故障类别、不同故障程度以及不同运行转速下的轴承故障数据集提取到的最优特征组有一定的差别。比如,本文算法和Chi+KNN算法在数据集3下的最优特征组分别为{4、10}和{2、4、7、14、16},可以看出本文算法去除了不相关特征以及冗余特征,最优特征组更精简,且对于早期故障数据集3来说,本文算法选取的最优特征组具有更精确的分类,高于Chi+KNN算法2.39%,有较大提升。 如图3所示,本文算法与Chi+KNN算法选择的最优特征组对早期故障数据集1与数据集2的不同分类情况,不难发现图3a与图3c的分类更加清晰,且类内更加紧致,类间重叠性更低,能够准确地捕捉早期故障的微弱特征,对正常样本与异常样本进行精确识别,且精确度更高。 表4描述了在数据集1下的EKNN分类器对30个候选次优特征组的分类精确度。从实验结果可以看出,当最优特征组为F={f4、f7}时,精确度最高为0.97,且f4(幅度)属于波形特征,f7(均方根值)属于时域统计特征,表明选择AE信号波形特征和统计特征来构造混合特征具有有效性。 表4 30个候选次优特征组的分类精确度 实验2EKNN算法的K值敏感度分析。 将算法1得到的早期故障特征组应用于EKNN算法,对样本数据进行分类。由于在早期故障的多类别分类中,每个类的密度不同,仅使用两个样本之间的欧氏距离来决定样本标签会导致分类精确度下降,使得分类结果对K值敏感性较大。因此,当近邻大小K取值不同时,传统KNN分类器与本文的EKNN分类器具有较大的差别。实验2进一步分析K取值不同时(K=3,K=5,K=7,K=9),两种分类器对分类结果的影响。如图4所示,当K=5、K=9时,使用传统KNN和EKNN分类器对椭圆内的样本进行分类,其实际标签为内圈故障。然而,传统KNN分类器在K=5时,判断测试样本为内圈故障,K=9时为外圈故障,分类显然是不成功的。本文将一种新的密度计算加入到分类过程中,分类器能够在K=5或K=9时正确地对测试样本分类,早期故障样本的分类结果具有稳健性。 表5列出了6个数据集和4种K值在传统KNN、改进SFS+KNN和本文算法下的平均分类精确度。显然,早期生成的弱故障样本不易被区分,会对分类性能产生影响。从表5中可以看出,各算法在数据集4~数据集6的分类精确度均高于数据集1~数据集3,因为大尺寸裂纹12 mm比早期故障产生的小尺寸裂纹3 mm更易识别。 表5 在不同数据集、不同K取值下3种分类器的诊断性能 依据表5,本文算法与改进SFS+KNN算法、传统KNN算法在数据集1~数据集6,K={3、5、7、9}取值下的精确度差值如图5所示。其中平均差值1折线表明不同K值在同一数据集下,本文算法与改进SFS+KNN算法之间的平均精确度差值;平均差值2折线表明不同K值在同一数据集下,本文算法与传统KNN算法之间的平均精确度差值。图5中两条折线的共同点在于本文算法对其他两种算法在早期故障数据集1~数据集3的平均分类精确度差值都等于甚至大于在数据集4~数据集6的平均精确度差值。对比改进SFS+KNN算法,当K=3时,EKNN提高的平均精确度最少为1.78%;K=5时,EKNN提高的平均精确度最多为7.79%;对比传统KNN算法,当K={3、5、7、9}时,EKNN分别提高了13.73%、16.43%、11.40%和12.62%的平均精确度。虽然数据集1~数据集3为滚动轴承早期产生的故障数据,比数据集4~数据集6更难分类,更易判定失误,但本文算法对早期故障数据集1~数据集3的平均精确度高于传统KNN算法的14.93%,高于改进SFS+KNN算法的2.98%,高于改进SFS+KNN算法在数据集4~数据集6的平均精确度0.03%。 图6所示为本文算法与改进SFS+KNN在不同K值、不同数据集和8种故障类别的精确度差值。本文算法在K取值不同时,对8种类别的早期故障都能较好地进行分类识别,且精确度均有较大的提高。其中当K值为5时,对内圈故障的提高尤为显著;当K值为5、7、9时,对外圈的故障有显著提高。 实验3EKNN对比算法性能分析。 为验证基于距离和密度双维度计算的EKNN故障分类方法的有效性和鲁棒性,将8个类别的AE信号、6个数据集,在相同实验条件下,除与传统KNN算法进行比较外,还将其与不同的算法进行比较,精确度由式(10)计算得出。包括文献[13]的Chi+KNN算法、文献[15]的t-SNE+KNN算法、文献[16]的WKNN-FS算法和文献[17]的WAF-KNN算法。实验结果如表6所示,结果表明本文算法优于其他5种算法,比KNN、Chi+KNN、t-SNE+KNN、WKNN-FS和WAF-KNN算法分别高出13.9%、2.43%、32.25%、2.39%和4.81%。 表6 不同方法下的分类精确度 本文首先获取由AE信号的波形特征、时域特征、频域特征等构成的早期故障混合特征集;然后将内类紧致性和内间重叠性引入序列前向选择算法中,提取混合特征中的次优特征组作为EKNN分类器的输入;最后基于距离和改进的密度计算,得到最优平均分类概率并输出最优早期故障特征组,在线阶段标记该特征组对应的故障状态,实现滚动轴承故障的智能分类。本文所提方法有效地降低了由于故障信号之间的相关性和冗余对早期故障分类精确度的干扰,改进了传统的KNN分类器仅采用距离计算进行分类的能力,克服了传统KNN分类器受K值敏感性影响而不利于早期故障数据进行分类的问题,并最终提高了分类精确度。本文仅针对早期微弱信号提出了故障诊断方法,但实际应用中滚动轴承的故障数据难以完整获取,无法建立有效的训练模型。因此,如何在样本失衡情况下对滚动轴承进行故障诊断有待进一步研究。2.2 算法描述
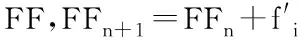
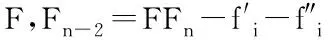
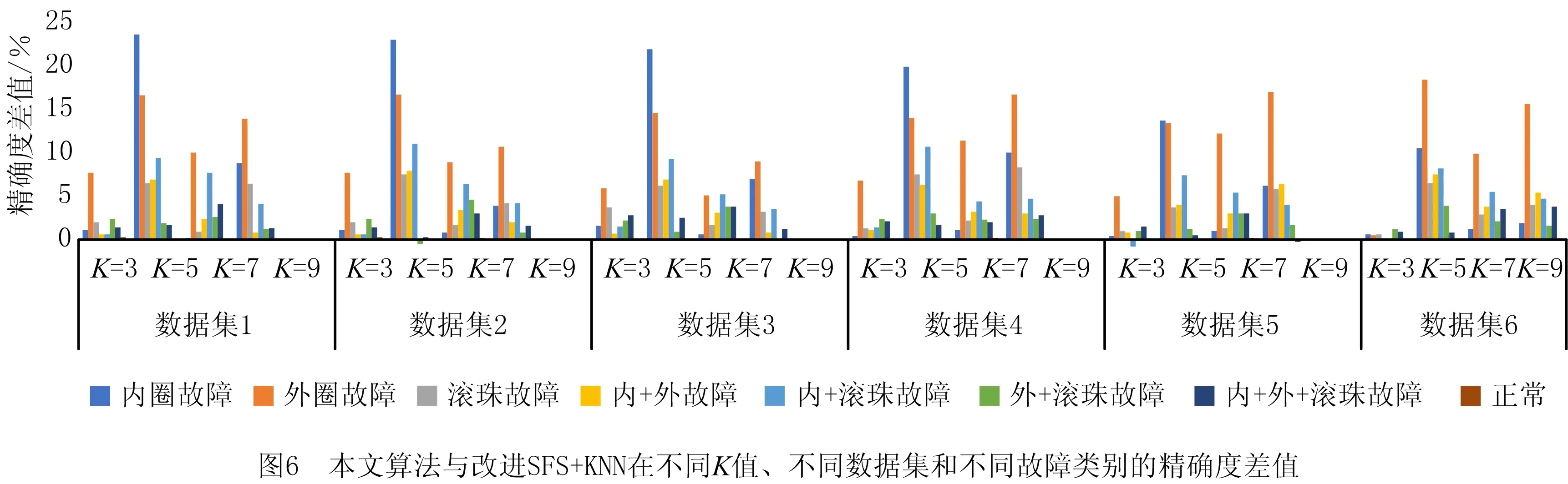
3 故障分类
3.1 相关定义
3.2 算法描述
4 实验及结果分析
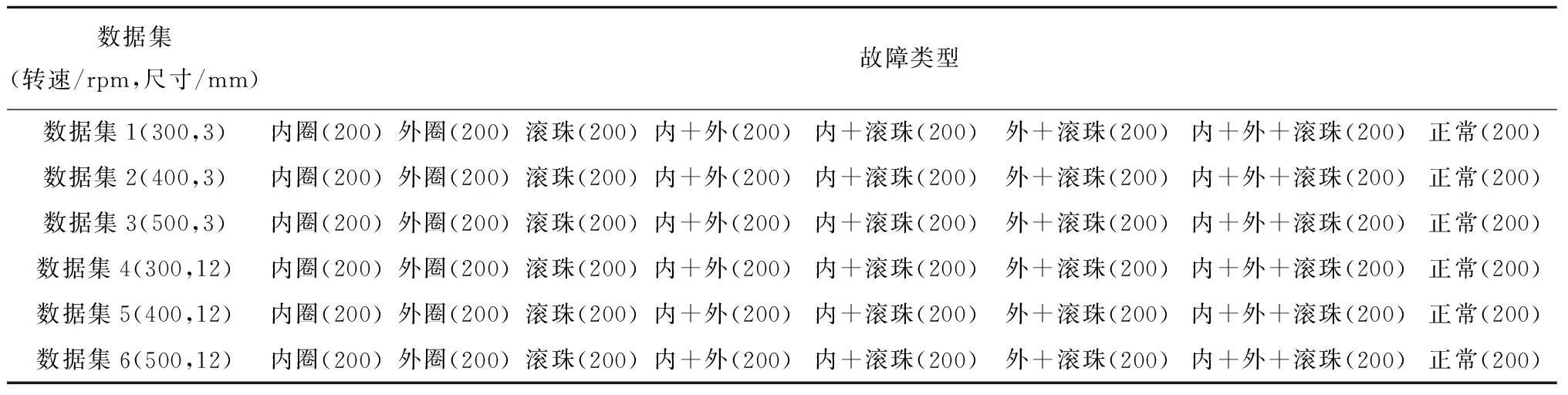
4.1 实验数据
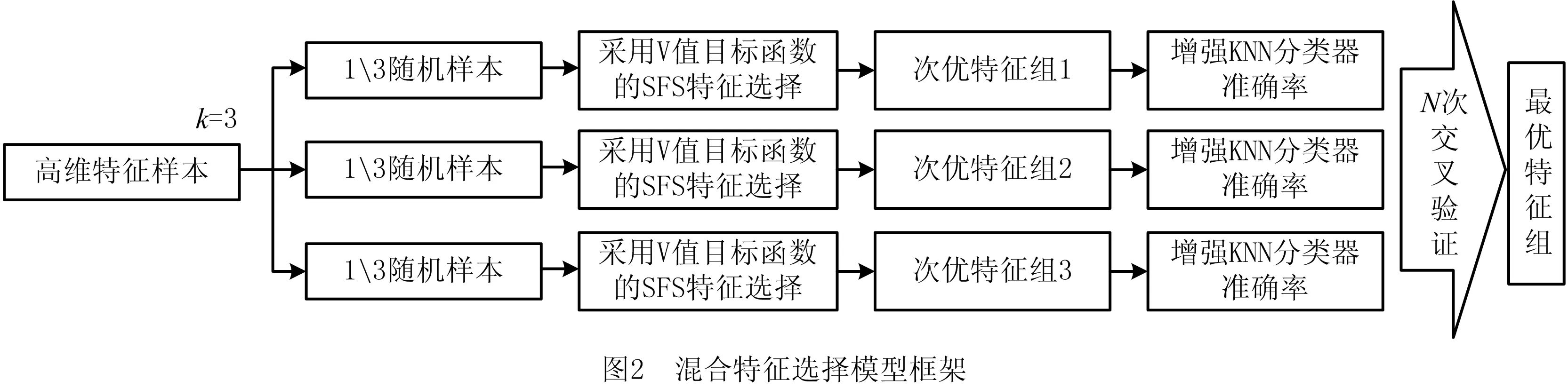
4.2 实验方案
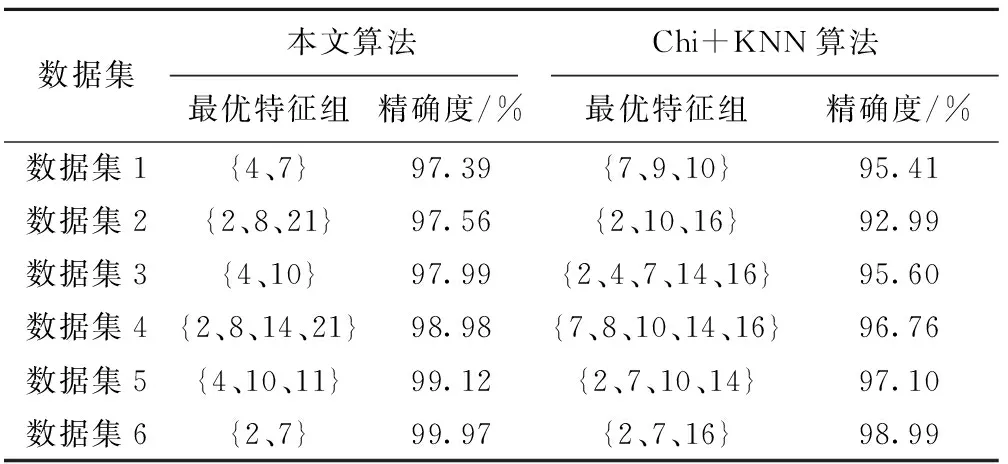
5 结束语
