极限状态法与容许应力法在铁路桥梁设计应用中的差异性比较

邓江涛

(中国铁路设计集团有限公司,天津 300308)

1 概述

极限状态法基于概率论和结构可靠度理论，考虑荷载变异、材料性能变异和工作条件的不同，采用概率统计方法和可靠度指标将各种影响因素转化为多分项系数形式[1-4]，已广泛应用于建筑、公路、水利、轨道交通等行业的结构设计中[5-8]；容许应力法以线性弹性理论为基础，以构件危险截面的某一点或某一局部的计算应力小于或等于材料的容许应力为准则[5]。容许应力法设计应用简便，是工程结构中的一种传统设计方法，目前主要在铁路工程设计中应用。以全预应力构件为例，综合两种设计方法，将控制指标分类，一般性指标对比见表1。新的铁路桥涵极限状态法设计已于2019年6月起正式应用在新建铁路项目上，以概率理论为基础、按分项系数表达的极限状态设计方法避免了容许应力法单一安全系数过于经验笼统、各种结构具有比较一致的安全水平等不足[9-12]，能更好地与国际接轨。

表1 全预应力构件一般性检算指标对比

当前桥梁结构设计仍然面临着设计规范转轨的过渡期，还存在如计算工具滞后、实际工程应用经验缺乏等问题，随着新规范的不断应用，这些问题必然会逐步得到解决，容许应力与极限状态两种方法在实际工程应用中的深入比较也将越来越广泛[13-20]。

针对商合杭铁路(48+80+48) m连续梁试设计，开展了基于极限状态法连续梁全过程设计，通过比较分析得出了连续梁设计中的主要检算指标相互关系以及极限状态法与容许应力法两种方法的差异。

2 基于极限状态法(48+80+48) m连续梁结构设计

2.1 构造尺寸

梁全长为177.5 m，计算跨度为(48+80+48) m，中支点截面中心线处梁高6.335 m(为方便考察两种方法的差异性，计算指标与限制的比值控制在5%以内，此处梁高为调整后的试算梁高)，跨中9 m直线段及边跨13.25 m直线段截面中心线处梁高3.535 m，梁底下缘按二次抛物线变化。边支座中心线至梁端0.75 m，梁缝分界线至梁端0.10 m。边支座横桥向中心距5.60 m，中支座横桥向中心距5.90 m，如图1～图4所示。

图1 连续梁立面(单位：cm)

图2 连续梁平面(单位：cm)

图3 连续梁中跨跨中截面(单位：cm)

图4 连续梁中支点截面(单位：cm)

梁体结构为单箱单室、变高度、变截面箱梁，底板、腹板、顶板局部向内侧加厚，均按直线线性变化。全联在端支点、中支点处设横隔板，横隔板设有孔洞，供检查人员通过。施工方法采用悬臂施工法。

2.2 主要技术指标及主要设计荷载

设计速度350 km/h，为无砟轨道，线间距5.0 m，采用ZK活载，二期恒载按180 kN/m计，支座不均匀沉降取20 mm。

2.3 按极限状态法检算结果及主要指标分析

建立Midas有限元模型，全桥共计64个梁单元，提取内力，主要检算指标如表2所示。

由表2可知，(48+80+48) m连续梁各个检算指标均满足规范，分析各指标富余度，对连续梁来说，起主要控制作用的检算指标按控制程序排序为：正截面抗弯(运梁车)、正截面抗裂(运梁车)、正截面抗裂(运营)、正截面抗弯(运营)、斜截面抗弯(运梁车)、斜截面抗裂性、斜截面抗弯(运营)，对于常规连续梁，控制设计的主要指标为承载能力极限状态下的抗弯性和正常使用极限状态下的抗裂性，设计时应优先满足承载能力和抗裂性两个指标。

此外，当正截面抗弯性能满足后，斜截面抗弯抗剪可自动满足。截面承载能力越大，抗裂性更好，但截面承载能力满足抗裂性并不一定满足，尤其是在结构尺寸与钢束配置不算富余的情况下，二者没有一一对应的关系，设计时需要分别考虑。

表2 极限状态法检算指标汇总

承载能力极限状态下的抗弯性为主要的控制指标之一，进一步分析承载能力极限状态，将规范里的基本组合1～基本组合6的抗力曲线如图5、表3所示。

图5 正截面承载能力对比曲线

表3 承载能力指标检算汇总

分析图5、表3可知，在承载能力检算中，对于边跨正弯矩区，按照控制的程度排序为：基本组合2，3，5，4，1，6；对于中支点负弯矩区，按照控制的程度排序为：基本组合2，6，3，5，4，1；对于中跨正弯矩区，按照控制的程度排序为：基本组合2，3，5，1，4，6；由此可知，对于全梁段截面，基本组合2最不控制，基本组合1，3，4，5在各截面会因弯矩正负号有所差异，但数值相差不大。

3 极限状态法与容许应力法对比分析

为考察极限状态法与容许应力法两种方法的差异性，一方面，按照第2节的结构尺寸及钢束配置按容许应力法复算，另一方面，根据复算结果进行同精度设计，若按容许应力法检算后结构需要加强，则按满足1.05倍控制指标限值的原则进行加强，反之，若结构富余，同样按满足1.05倍控制指标限值的原则进行减少。

3.1 按容许应力法复算

采用容许应力法复算，各检算指标汇总见表4。表4中未列出的基于运营阶段使用安全考虑的竖向变形、竖向残余变形、竖向梁端转角、横向变形、竖向自振频率以及基于成桥过程安全考虑的各检算指标与表2一致。

由表4可见，起主要控制作用的检算指标按控制程序排序为：正截面抗弯(运梁车)、正截面抗弯(运营)、正截面抗裂(运梁车)、正截面抗裂(运营)、斜截面抗裂性、斜截面抗弯(运梁车)、斜截面抗弯(运营)，各检算指标控制程度顺序与表2结论基本一致。

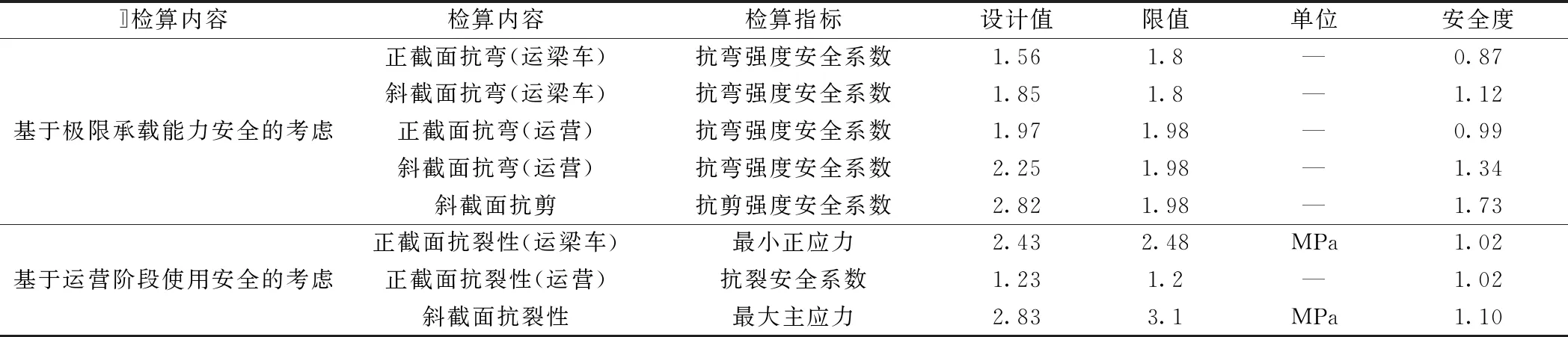
表4 容许应力法复算结果汇总

此外，按照第2节的结构尺寸及钢束配置按容许应力法复算，运梁车工况及运营工况下的正截面抗弯强度检算不满足限值要求，表明容许应力法更保守，以概率理论为基础、按分项系数表达的极限状态设计方法，依据作用的变异性，科学采用恒载、活载、风荷载、温度荷载等的分项系数及组合系数，使得设计结果更贴近工程实际。

3.2 按容许应力法同精度设计及经济性对比分析

表4分析表明，采用容许应力法复算后个别指标不满足限值要求，说明需要对结构进行加强。为进一步研究极限状态法与容许应力法两种方法在工程用料上的差异性，通过加强配束，来提高运梁车工况及运营工况下的正截面抗弯强度。

结构尺寸与表2所采用的一致，将边跨底板束规格由14-φ15.2 mm调整为17-φ15.2 mm，中跨底板束规格由15-φ15.2 mm调整为18-φ15.2 mm，通过增加钢束使正截面强度安全系数、正截面抗裂安全系数、预应力钢束应力比的安全度达到1.05以内，各检算指标汇总见表5，工程数量变化分析见表6。

表5 加强钢束后检算指标汇总

表6 纵向预应力钢束质量及调整比例

表5、表6分析表明，通过加强边跨底板束和中跨底板束，采用容许应力法检算的各指标满足规范要求，由此产生的钢束增量为10.09 t，每联增加比例7.7%，每联增加工程造价约9.93万元。

4 结论

对(48+80+48) m连续梁通过极限状态和容许应力两种方法试设计对比分析，可以得到以下结论。

(1)采用极限状态法进行全过程结构设计，分析主要检算指标，承载能力极限状态下的抗弯性和正常使用极限状态下的抗裂性是主要的控制指标，设计时应优先满足。此外，当正截面抗弯性能满足后，斜截面抗弯抗剪一般可自动满足。截面承载能力越大，抗裂性更好，但截面承载能力满足抗裂性并不一定满足，尤其是在结构尺寸与钢束配置不算富余的情况下，二者没有一一对应的关系，设计时需分别考虑。

(2)按容许应力法复算，运梁车工况及运营工况下的正截面抗弯强度检算不满足限值要求，表明容许应力法更保守，以概率理论为基础、按分项系数表达的极限状态设计方法，依据作用的变异性，科学采用恒载、活载、风荷载、温度荷载等的分项系数及组合系数，使得设计结果更贴近工程实际。

(3)按容许应力法同精度设计，通过加强边跨底板束和中跨底板束，采用容许应力法检算的各指标满足规范要求，增加钢束用量10.09 t，增加7.7%，每联工程造价增加约9.93万元。