基于核心素养的高三数学试卷讲评策略——以一道解析几何定点问题为例

广东省广州市花都区秀全中学(510800) 董大新

如何上好高三数学试卷讲评课,是值得探讨的问题. 笔者认为,高三数学试卷讲评课是提升学生的关键能力和应试策略的教学活动,要把握课型特征,选择适切的讲评策略,追求优质高效的讲评效果.

1 高三数学试卷讲评课的课型特征

(1)高三数学试卷讲评课的教学目标

高三数学试卷讲评课是以“查漏补缺、优化策略、提升素养”为主要任务的课型,其主要教学目标是弥补知识缺陷,积累解题经验,优化思维素质,提高应试能力.

(2)高三数学试卷讲评课的教学要求

高三数学试卷讲评课的教学要求是: 把握考情,查漏补缺,突出重点,深度思维,反思优化,培养意志品质,提升关键能力,优化应试策略.

(3)高三数学试卷讲评课的操作程序

高三数学试卷讲评课的常见操作模式有两种[1]:

正误辨析式: 展现错误—辨析纠错—形成解法—变式练习—激励评价.

引申拓展式: 展现解法—失误分析—问题变式—激励评价—变式训练.

2 高三数学试卷讲评课的教学策略

核心素养导向的高三数学讲评,要把“怎么想到的”思维过程展示给学生,要在“最近发展区”设计变式练习[2];要精准分析错因,注重问题本质,优化解题方法[3]. 笔者认为,高三数学试卷讲评课的教学策略有: 注重学生参与,注重错因分析,突出讲评重点,注重变式探究.

(1)注重学生参与

高三数学试卷讲评课要注重学生主动参与: 一是引导学生关注自身进步,自主纠错,自我评价,提升学好数学的自信心;二是引导学生自我反思,举一反三;三是引导学生优化解法,深度思维,积累解题经验.

(2)注重错因分析

高三数学试卷讲评课要对失误原因进行恰当归因. 学生在考试中常出现过失性丢分和知识性失分,如审题不清,计算有错,表达不规范,基础知识掌握不牢[4]. 因此,在高三数学试卷讲评课中要通过示错教学,找到错误症结,优化纠错策略. 通过对学生在测试中存在的问题,及时查漏补缺,完善知识结构.

(3)突出讲评重点

高三数学试卷讲评课要突出讲评重点. 一是讲评通性通法,强化审题训练,展示思维过程,寻求试题解法的改进与优化, 引领学生学会解题; 二是讲评出错原因, 分清错误类型,引导学生弥补解题缺陷,夯实基础知识,完善数学认知结构;三是讲评试题本质,通过问题变式,强化问题探究意识,发展学生的应变能力和创新意识;四是讲评应试策略,规范解题过程,强化得分意识,让学生“少丢分、多得分”.

(4)注重变式探究

高三数学试卷讲评课要注重变式探究. 变式探究可从两个方面展开: 一是一题多解,拓宽解题思路,展现火热的数学思考,寻求解法的改进与优化;二是一题多变,通过问题变式建构知识之间的内在联系,在“变”的现象中发现“不变”的本质,在“不变”的本质中探索“变”的规律,强化问题探究意识,优化思维品质,培养应变能力和创新能力.

3 高三数学试卷讲评课的教学案例

下面以一道解析几何定点问题为例,分享我们的实践.

题目: (2020年广州市综合测试(一)文科数学第20 题)已知⊙M 过点A(0), 且与⊙N : (x++y2= 16内切,设⊙M 的圆心M 的轨迹为曲线C.

(1)求曲线C 的方程;

(2)设直线l 不经过点B(0,1)且与曲线C 相交于P,Q两点. 若直线PB 与直线QB 的斜率之积为判断直线l 是否过定点,若过定点,求出此定点坐标;若不过定点,请说明理由.

讲评实录:

教学环节1: 展现错误,寻找错因.

教师: 本题主要考查直线、圆、椭圆的基础知识,考查数形结合与分类讨论思想,考查运算求解能力,得分率较低. 先看第(1)问解法(用多媒体平台展示错误解法):

教师: 很好! 从答题情况看,第(1)问的主要失误是记忆不牢,不能从圆与圆内切找出正确的轨迹条件,不能按椭圆定义判断所求轨迹的类型. 再看第(2)问的如下解法:

依题意,直线BP,BQ 的斜率均存在且不为0,

学生: 点P 的纵坐标出错.

教师: 确实,点P 的纵坐标求错了. 在第(2)问求解中,还有哪些失误?

学生1: 先求P,Q 两点的坐标,再求直线PQ 的方程,但求错了P,Q 两点的坐标.

学生2: 求对了P,Q 两点的坐标,但直线PQ 的斜率算错了.

学生3: 先设直线l 的方程,再作出判断,结论正确,但没有分类讨论.

教师: 从答题情况来看,第(2)问的主要失误有二: 一是“会而不对”,知道解题方法,但计算不过关,导致结论出错;二是“对而不全”,结论正确,但缺少对直线l 的斜率是否存在进行分类讨论, 解题过程不完整. 下面探讨第(2)问的解法.

教学环节2: 深度理解,形成解法.

教师: 第(2)问的已知条件是什么? 解题目标是什么? 如何达成解题目标?

学生4: 已知条件有直线l 与曲线C 相交于P,Q 两点,且不经过点B(0,1).

学生6: 解题目标是判断动直线是否过定点.

学生7: 要达成解题目标,需建立已知条件和解题目标的联系.

教师: 如何判断动直线是否过定点?

学生8: 先求动直线的方程,再作判断.

教师: 如何求动直线的方程?

学生9: 根据已知条件先求P,Q 两点坐标,再求直线l的方程.

学生10: 先设直线l 的方程,再由直线PB 与直线QB的斜率之积为确定直线l 的方程.

通过上述启发引导,学生独立解题,教师投影第(2)问的两种解法:

综上所述,直线l 过定点(0,0).

教学环节3: 问题变式,把握本质.

教师: 改变题目条件,可得变式1.

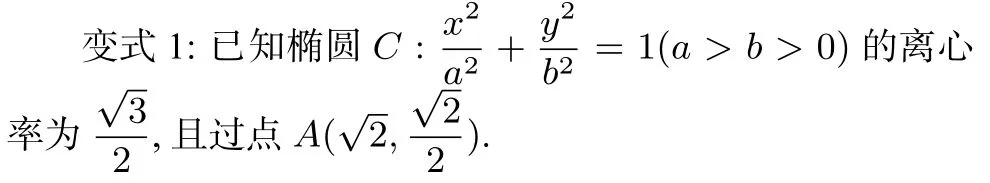
(1)求椭圆C 的方程;

(2)设直线l 不经过点B(2,0)且与椭圆C 相交于P,Q两点. 若直线PB 与直线QB 的斜率之积为判断直线l 是否过定点,若过定点,求出此定点坐标;若不过定点,请说明理由.

学生独立求解,教师展示学生11 的解法:

综上所述,直线l 过定点(0,0).

教师追问: 由上述题目与变式1,有何发现?

(1)求曲线C 的方程;

(2)设直线l 不经过点B(2,0)且与曲线C 相交于P,Q两点. 若直线PB 与直线QB 的斜率之积为判断直线l 是否过定点,若过定点,求出此定点坐标;若不过定点,请说明理由.

学生解题,教师展示学生14 的解法:

教师: 将变式1、变式2 一般化,有何结论?

学生15: 设直线l 不经过点B(2,0) 且与椭圆C :

教学环节4: 激励评价,变式训练.

教师: 回顾上述考题与变式的求解过程,有何感悟?

学生16: 定义法和直译法是求曲线方程的基本方法.

学生17: 直线过定点问题的基本解题思路是求出该直线的方程.

学生18: 定点问题要注重运算求解和分类讨论.

教师: 善于归纳总结,善于知识迁移! 双曲线的直径也有类似性质,请同学们课后编一道双曲线背景下的直线过定点问题并予以解决.

接下来,教师布置如下3 道变式题让学生求解.

(1)求曲线C 的方程;

(1)求曲线E 的方程;

(2)直线y = kx+m 与曲线E 相交于P,Q 两点,若曲线E 上存在点R,使得四边形OPRQ 为平行四边形(其中O 为坐标原点),求m 的取值范围.

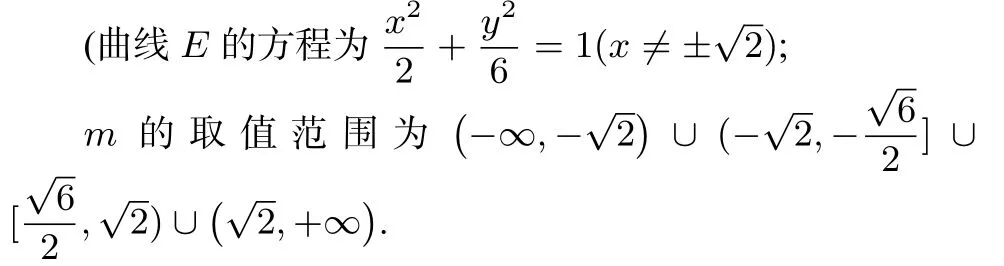
核心素养导向的高三数学试卷讲评课要依据课型特征和学生实际,选择恰当的教学策略,提升关键能力,优化应试策略,为情境而教,为素养而教.