2020年高考数学对数学文化的考查*

华东师范大学教师教育学院(200062) 纪妍琳

1 引言

2003年教育部颁布的《普通高中数学课程标准(实验)》中明确提出了对数学文化的学习要求[1]. 教育部考试中心发布的《关于2017年普通高考考试大纲修订内容的通知》中增加中华优秀传统文化的考核内容, 在能力要求内涵方面,增加了对数学文化的要求[2]. 2018年颁布的《普通高中数学课程标准(2017年版)》也提出:“数学文化应融入数学教学活动. 在教学活动中,教师应有意识地结合相应的教学内容,将数学文化渗透在日常教学中,引导学生了解数学在科学技术、社会发展中的作用,感悟数学的价值,提升学生的科学精神、应用意识和人文素养;将数学文化融入教学,将有利于激发学生的数学学习兴趣,有利于学生进一步理解数学,有利于开拓学生视野、提升数学学科核心素养[3].”课程标准是数学教学实施的指南,新修订的课程标准更是高考的向导. 高考数学是选拔人才的重要手段,发挥着对中学数学教育的导向作用,故更应体现数学的文化价值. 在深化新时代高考内容改革的背景下,高考评价体系将立德树人确定为高考的核心功能, 将“核心价值”、“学科素养”、“关键能力”和“必备知识”确定为高考考查内容. 具体到数学学科,高考语境下的数学学科素养包括“数学文化”等四项内容[4]. 可见,无论是教学还是评价,“数学文化”都是倍受关注的内容.

本文从数学文化的视角对2020年全国各地高考题进行考察,分析文化背景下的高考试题编制特征,以期为数学教学实践提供借鉴.

2 全国各地2020年高考数学试题中的数学文化

对于“数学文化”的内涵,顾沛认为,狭义的数学文化指数学思想、精神、方法、观点,以及它们的形成和发展;广义的定义还包含数学史、数学美、数学教育、数学与人文的交叉、数学与各种文化的关系等[5].《普通高中数学课程标准(2017年版)》(以下简称《标准》)对数学文化内涵的界定与顾沛的界定相似,同时具体提出: 数学文化包括数学在人类生活、科学技术、社会发展中的贡献和意义,以及与数学相关的人文活动.“基于数学史的数学文化内涵分析框架”将数学文化分为“知识源流”、“学科联系”、“社会角色”、“审美娱乐”和“多元文化”五个维度[6]. 在该框架的基础上,本文结合《标准》中的相关要求和高考数学试题的特点,将各维度的内涵进行补充、拓展,推广到更一般的数学文化中,得到数学文化视角下的高考数学试题分析框架,如表1 所示.

表1 数学文化视角下的高考数学试题分析框架

基于该分析框架,本文对2020年全国各地高考试题中体现数学文化的试题进行汇总,如表2 所示. 若同一题目在不同版本的高考卷中均出现(例如,全国1 卷理科数学与文科数学第3 题相同),本文不作重复呈现. 对于以现实生活的事物作为背景的题目,若问题没有突出数学在解决特定现实情境问题的作用或必要性,且试题主要目的在于利用现实背景作为问题情境,考察学生将现实问题抽象为数学问题或在现实情境中应用数学知识的能力,问题本身与现实生活距离较远,则不将其作为“社会角色”的一种体现(例如抽球问题、骰子点数问题).

表2 全国各地2020年高考数学试题中体现数学文化的题目分布

2.1 知识源流

此类高考试题将数学知识发展的历史过程、重要结果、主要任务、关键事件及其贡献作为题目的背景,一方面创设了考察特定知识与技能的生动情境,另一方面揭示了“知识源流”,渗透数学文化. 2020年各地高考数学试题中,仅有浙江卷第11 题以“知识源流”作为试题的数学文化背景.

(2020年浙江卷第11 题)我国古代数学家杨辉,朱世杰等研究过高阶等差数列的求和问题,如数列就是二阶等差数列. 数列的前3 项和是____.

评析: 中国古代数学在高阶等差数列求和等方面取得过举世闻名的创造性成果, 沈括的“隙积术”、杨辉的“堆积术”和朱世杰的“垛积术”是求解高阶等差数列方面的重要贡献. 对于数列的 前n 项和, 实际上杨辉在13 世纪时已经给出三角垛求和公式:1+(1+2)+(1+2+3)+···+(1+2+3+···+n) =[7]. 此题仅考察了简单的数列计算,考生通过数列通项公式即可得到前3 项,再进行求和即可得到答案为10. 同时,试题对所考察的数列背景进行了简略的介绍,揭示了知识源流,但仅通过简单的话语学生还不足以使了解中国古代数学在等差数列方面的突出成就. 在日常教学中,教师可以对《九章算术》、《张丘建算经》等中国古代数学著作的数列问题进行介绍,帮助学生了解数列知识的历史与应用.

2.2 学科联系

《标准》在“课程性质”中指出:“数学是自然科学的重要基础,并且在社会科学中发挥着越来越大的作用. ”在社会科学、人文科学中,数学也扮演中重要的角色. 部分高考题以其他学科作为数学试题的背景,一方面为考察学生的数学学科核心素养创设了现实情境或科学情境,另一方面体现了数学的科学价值,渗透了数学文化. 在2020年各卷别高考试题中,出现了以生物、音乐、建筑、通信技术等不同学科背景的试题,突显了数学学科与其他学科之间的密切联系.

(2020年全国Ⅱ卷文科数学第3 题)如图, 将钢琴上的12 个键依次记为a1,a2,··· ,a12. 设1 ≤i < j < k ≤12.若k—j = 3 且j—i = 4,则称ai,aj,ak为原位大三和弦; 若k—j =4 且j—i=3,则称ai,aj,ak为原位小三和弦. 用这12个键可以构成的原位大三和弦与原位小三和弦的个数之和为( ).

A. 5 B. 8 C. 10 D. 15

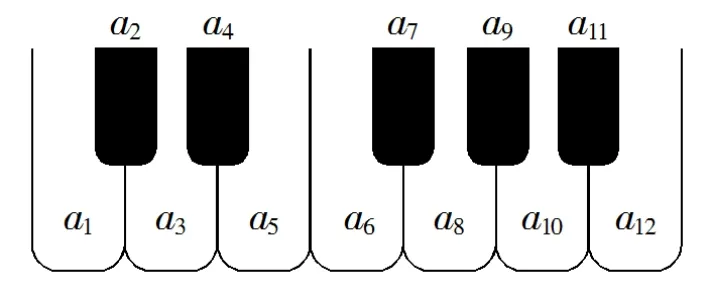
评析: 此题以音乐学科中的“原位大三和弦”和“原位小三和弦”为背景,考察了学生对新定义的理解能力和对于列举法的掌握. 事实上,“原位大三和弦”和“原位小三和弦”的个数,均等于k −˙l =7(1 ≤i

(2020年全国Ⅲ卷理科数学第4 题)Logistic 模型是常用数学模型之一,可应用于流行病学领域. 有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t 的单位:天)的Logistic 模型: I(t)=其中K 为最大确诊病例数. 当I(t∗) = 0.95K 时,标志着已初步遏制疫情,则t∗约为(ln19 ≈3)( ).

A. 60 B. 63 C. 66 D. 69

2.3 审美娱乐

在“基于数学史的数学文化内涵分析框架”中,“审美娱乐”是指数学美与趣味数学[10],关注的是数学中的对称美、奇异美、简洁美、统一美等. 2020年全国各地高考题中并无涉及数学美与趣味数学的题目,但部分题目用数学的视角刻画了建筑等现实世界中的事物的和谐美,本文也将其纳入“审美娱乐”的范围进行分析.

(2020年全国Ⅱ卷理科数学第4 题)北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层,上层中心有一块圆形石板(称为天心石),环绕天心石砌9 块扇面形石板构成第一环,向外每环依次增加9 块,下一层的第一环比上一层的最后一环多9 块,向外每环依次也增加9 块,已知每层环数相同,且下层比中层多729 块,则三层共有扇面形石板(不含天心石)( ).

A. 3699 块 B. 3474 块 C. 3402 块 D. 3339 块

评析: 2020年全国Ⅱ卷理科数学第4 题刻画了天心石环绕扇形石板中, 每层石板块数按层数对应成等差数列的规律. 解决此题时, 考生需要将数列从问题情境中抽象出来, 由题意得, a1= 9,d = 9, 每层有n 环,则第上、中、下层三层的石板数分别为Sn,S2n,S3n, 则S2n−Sn= n2d = 729, 解得n = 9, 由等差数列求和公式可得S3n= a1·3n+3402,选C.此题察了等差数列及其求和公式的相关知识,从数学的角度揭示了天坛扇形石板排布的和谐美. 类似的题目在近年的高考试题中并不少见,例如2019年高考数学全国Ⅰ卷第4 题以“断臂维纳斯”为背景,用“黄金分割”揭示了雕塑之美,等等. 数学可以刻画现实世界中的简洁美、对称美、和谐美和周期美.学会审美不仅可以陶冶情操,而且能够改善思维品质.《标准》也将“美与数学”作为选修D 类课程的专题之一[3],因此从数学的角度刻画审美的共性也应是数学文化的重要表现.在新课标的指引下,教师在数学教学实践中应当关注对“审美娱乐”相关内容的渗透,既关注数学本身的美与趣味,也关注运用数学对现实世界中的“美”的刻画.

2.4 社会角色

数学与人类生活和社会发展密切关联,数学的应用已经渗透到现代社会及人们日常生活的各个方面. 2020年高考数学试题以沙漠治理、疫情防控等现实情境作为试题背景,呈现数学知识在社会发展中所扮演的社会角色,发挥高考试题的育人价值.

(2020年新高考全国Ⅰ卷第4 题)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间. 把地球看成一个球(球心记为O),地球上一点A的纬度是指OA 与地球赤道所在平面所成角,点A 处的水平面是指过点A 且与OA 垂直的平面. 在点A 处放置一个日晷,若晷面与赤道所在平面平行,点A 处的纬度为北纬40◦,则晷针与点A 处的水平面所成角为( ).

A. 20◦B. 40◦C. 50◦D. 90◦

评析: 新高考全国Ⅰ卷以赤道日晷作为背景,涉及了二面角、直线与平面垂直等知识点. 赤道日晷的原理示意图如图所示. 解决此题的关键在于根据题目所给出的有关日晷的描述建立起如图1 所示的几何表征,所求∠2 与纬度∠1 之和为90◦,答案选C.此题以中国古代文化——日晷,作为题目的的背景,考察了学生有关于球、二面角、线面垂直等有关知识和数学抽象能力. 学生在解决此题的过程中,了解了日晷的设置原理,体会了数学在测定时间中所发挥的作用.

图1

2.5 多元文化

多元文化”是指不同文明、不同地域的数学家在同一数学课题上的贡献与意义,以及与数学相关的人文活动.《标准》在“教科书编写建议”中强调:“要把数学文化融入到数学学习内容中,充分体现数学的文化价值,体现数学对于人类文明发展的贡献. 在内容中,既要结合数学史适时吸收一些体现中华民族优秀传统文化的素材;也要借鉴异域文化的优秀成分,展现高中数学教科书应有的国际视野”[3].“多元文化”的渗透有助于学生感受不同时空下的数学家对同一数学课题的火热探讨,形成更加开阔的视野和胸怀. 2020年高考数学北京卷的第10 题以圆周率的计算为背景,探讨了我国古代数学家刘徽与阿拉伯数学家阿尔·卡西求解圆周率时所采用的方法,体现了不同文化背景下的数学家对于求解圆周率所作出的贡献,同时也揭示了“知识源流”.

(2020年北京卷第10 题)2020年3月14日是全球首个国际圆周率日(πDay). 历史上,求圆周率π 的方法有多种,与中国传统数学中的“割圆术”相似. 数学家阿尔·卡西的方法是: 当正整数n 充分大时,计算单位圆的内接正6n 边形的周长和外切正6n 边形(各边均与圆相切的正6n 边形)的周长,将它们的算术平均数作为2n 的近似值. 按照阿尔·卡西的方法,π 的近似值的表达式是( ).

由上述迭代运算, 求出Cn后, 卡西指出在半径为1 的单位圆中利用勾股定理可求得圆的内接正3×2n边形边长BHn,随后基于相似三角形的性质求出此圆的外切正3×2n边形周长,再由圆的内接正3×2n 边形周长和圆的外切正3×2n 边形周长的平均值作为圆周长的近似值,进而得到圆周率的估算值. 北京卷第10 题简略呈现了阿尔·卡西求解圆周率所用到的方法,同时联系了刘徽的“割圆术”,符号学生的认知水平,呈现了多元文化,同时也呈现了圆周率相关知识发展的历史片段.

3 数学文化与问题的可分离程度

本文所考察的高考数学试题将数学文化作为问题的背景,创设了特定的问题情境.《标准》提出要在现实情境、数学情境或科学情境下提出问题[3],涉及数学文化的高考试题一般是“非数学情境”,对学生的数学抽象素养和数学建模素养有一定要求. 对于问题情境在问题解决过程中的作用,李健从“数学问题的翻译”和“数学结果的翻译”两个维度对问题解决中的情境作用进行水平划分. 在此基础上,本文参考李健所给出的各维度的的操作性定义,将“情境与问题的可分离程度”将情境分为“分离式情境”、“可分离情境”和“不可分离情境”,如表3 所示,对涉及数学文化的高考试题进行进一步的考察.

表3 数学文化与问题的可分离程度分类

对表1 所汇总的道题目进行分类统计,结果如图2 所示.25%的涉及数学文化的试题情境为“分离式情境”,对题目所涉及的历史人物或现实背景进行简述,再用数学化的语言对情境进行分析,题目已经完成数学化,学生可以忽视数学文化背景,直接在数学情境中解决问题,“分离式情境”数学文化试题通过附加式的方式也起到了一定的育人导向作用,但由于学生高考时注意力有限,往往将注意力集中与数学问题本身而直接忽视了试题的文化背景;65%的涉及数学文化的试题的情境是“可分离情境”,试题基于数学文化为学生创设现实情境或科学情境,学生解决该问题时需要将数学问题从问题情境中剥离出来,但不需要根据情境的特殊性对数学问题增加限制条件,完成数学化之后,并不需要返回情境进行检验,此类问题既渗透了数学文化,又考察了学生的数学抽象素养和数学建模素养,是备考中所需重点关注的题型;10%的涉及数学文化的试题情境为“不可分离情境”,学生在解决这类问题时,既需要将数学问题从特定情境中剥离出来,有需要基于情境的特殊性对数学问题和数学结果作出进一步的限制,此类问题将情境与数学内容紧密的联结,忽视情境的特殊性将得出错误的结果.

图2

4 结论与启示

通过“文化类型”与“情境与问题的可分离程度”这两个角度,本文考察了2020年全国各卷别高考数学试题,可以得到以下结论: 其一,高考数学试题注重对数学文化的渗透,积极发挥育人价值,试题较多体现“学科联系”与“社会角色”,“知识源流”、“审美娱乐”、“多元文化”的体现相对较少;其二,涉及数学文化的高考试题,情境主要为“可分离情境”,忽略数学文化背景无法解决相应的问题,但“不可分离情境”较少.

基于上述结论,可以得到以下启示:

(1) 丰富试题情境, 多角度渗透数学文化. “知识源流”、“审美娱乐”与“多元文化”是数学文化的重要组成部分,是数学文化试题编制的重要视角,试题编织者可增加这三方面的试题编制,丰富试题情境.

(2)关注数学抽象与数学建模,提升问题解决能力. 现今的高考数学中,“非数学情境”的试题越来越多.“数学文化”试题是“非数学情境”试题的一种,对学生的数学抽象素养和数学建模素养提出了一定的要求. 在日常学习中,学生在问题解决时应该关注对于情境的抽象能力和建模能力,以更好地进行问题解决.

(3)将数学文化试题作为教学素材,丰富知识学习与应用的情境. 涉及数学文化的高考数学试题,可作为教师的教学素材. 在实际教学中,教师可以从学生的认知出发,对数学文化背景的高考试题进行改编. 对学有余力的学生,可向其介绍试题相应的文化背景;对于较感兴趣的学生,可鼓励以相应主题进行数学写作,让数学课堂散发文化的芬芳.