西蒙数学视角下的初中几何模型复习课设计*——以“手拉手模型复习”为例

广东省广州市江南外国语学校(510240) 黎乐锋

1 发现问题

中考复习课堂中, 老师总希望学生能细嚼每个知识点,每节复习课都让学生进行知识再现、进行课堂训练巩固等过程. 在这类课堂中,以老师为主导,学生完成老师设置的一系列教学活动,学生被动复习,亦步亦趋去完成老师心中的“教学任务”.这种统一步调的教学方式,一般会忽视学生个体差异,学困生难以跟上,尖子生始终“吃不饱”.为了有效提高课堂效果,越来越多教师开展专题化复习.

专题化复习课堂要求较高,以知识点角度看,要求学生系统地掌握一系列的知识,明确各个公式和定理在每种题型中的地位和作用,强化知识的交叉互补,构建完整知识体系;以学生能力看,要重视数学思维能力的培养,注重数学核心素养的提高和数学解题策略的分析,提升“四能”. 在实际操作中,效果却不容易体现. 一些专题课堂中,教师在课堂里一讲到底,剥夺了学生的自主探索时间,难点重点都是被讲出来的,不是学生自己发现的,教学效果不言而喻.

有如下教学片段:

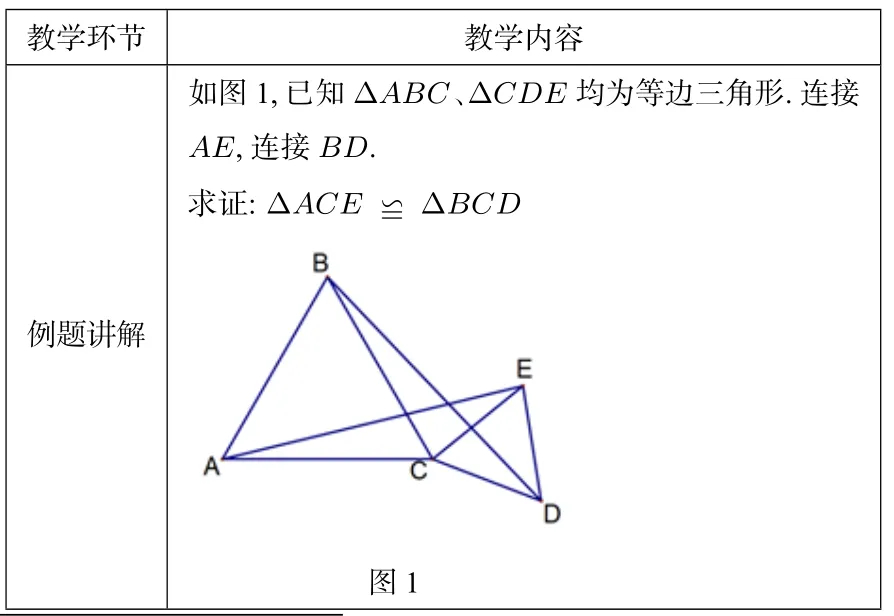
专题复习的引入,常以一道中等题,甚至一道较难题为起点. 这道题既与主要解题思路相关,又有一定挑战性的题目;既可简化抽象出基本模型,又可深化拓展出难题. 但在学生角度来看,后进生要在短短几分钟内跟上教师思路不容易,尖子生快速看穿思路后等待拓展,他们都需要教师作出合理且精确的引导. 然而,简化抽象和深化拓展都需要花费不少时间, 如时间把控不好, 整节课就很容易变成老师的“一言堂”,课堂效果大打折扣.

2 思考对策

自新标准提出后,课堂教学主张“以学定教”,教学活动要以“学生的学”为中心. 教学过程中,应该给予学生充足的学习自主,尽可能让学生自己明确目标,自主选择内容,先提问题,自发探寻方法,自行发现知识,学生控制过程,探究疑难,学生评价得失. 更有效的数学复习课堂,学生能够叙述、能提问、能操作、能发现的,教师均不越俎代庖. 初中的几何专题复习也应如是,同时需要更有效的教学方法.

2.1 借助西蒙数学理论,转“教学设计”为“学习设计”

一次教学研讨活动中,笔者接触到新的教学策略——“西蒙数学”.“西蒙数学”源自美国科学家赫伯·西蒙(H ·A · Simon) , 其理念是: 尊重认知起点, 搭建小步台阶; 从易到难编排题组; 知识求联, 技能求变; 突出小结, 训练从严[1][2][3][4][5].“西蒙数学”的课堂中,教师不直接传授数学知识给学生,而是给学生提出环环相扣的不同问题,形成问题链,并将其编写成“认知工作单”,让学生通过解决具体的数学问题,体验知识的形成过程,通过自我探索和建构,归纳或发现数学概念、定理或方法. 但在此过程中,不否定教师的示范作用. 教师适当示范解题过程是必要的. 除“做中学”,还要让学生懂得“例中学”,两者是“西蒙数学”的核心.

初中几何模型的学习中,每个基础模型都能衍生出一系列的题组,这与西蒙数学通过题组呈现问题的方式非常匹配.模型化专题训练能有效梳理中学生几何知识,加深印象,而西蒙数学教学法则为该训练课堂提供有效的方法. 因此,在几何复习课堂中,可将两者相互结合,以模型教学为主线,以西蒙数学认知工作单为载体,展开活动. 每个基础数学模型均可安排一到两个课时, 每个课时以题组方式呈现模型的“前世今生与将来”. 图形从简单到困难,设置关联的小问题,给学生创造“脚手架”,联系所需复习的知识,让学生在自己解决问题中构建模型、复习知识,实现“做中学”. 在完成每个题组后,教师引导学生完成题组小结,巩固认知. 课中或课后贯彻变式训练、通解训练,实现训练从严,提升复习效果.

2.2 采取产生式,改变知识呈现方式

认知心理学的观点认为,元认知的一个很重要的功能是监控记忆策略选择与使用的方式,是一个极其主动的加工过程.[6]教师的引导是外力,学生在教学过程中积极主动实现知识迁移才是重点. 在复习课堂中,要使每个学生都有提高,则每个学生都必须下笔做题和参加思考. 而在传统课堂中,引起学生参与这些课堂活动的, 则是教师的引入与情景创设.为使学生更主动思考,可采取产生式,来呈现知识内容.

数学的问题解决以及逻辑推理是基于产生式的. 数学问题均是以“如果…那么…”的形式出现. 用认知产生式的方法开展教学,能有效降低学习门槛,让大部分后进生也积极参与课堂活动. 捷克教育家夸美纽斯认为,教一个活动最好的方法是演示. 而荷兰数学家弗赖登塔尔认为,学一个活动最好的方法是做. 在如何把“演示”和“做”进行有机结合的问题上,西蒙数学教学法给出了有效的解决方式.其理论基础中的自适应产生式[7],是一种“条件转化成活动”的规则,只要条件一出现,活动就自动产生. 在解决一个复杂问题或作业时,需要许多产生式,它们构成了产生式系统. 而自适应产生式系统是一种能够使学生获得产生式的学习系统,这种学习方式,回归了人类学习的本原过程. 在几何模型复习课中,运用产生式能把学生学习主动性提高. 通过把题目分拆成多个互相连贯的产生式,可让学生由浅入深地通过做题完成知识迁移,促其有效理解几何基本模型的来由、变式与综合运用.

3 案例分析

为把理论与实践结合,笔者以西蒙数学的模式展开专题教学. 基于西蒙数学的教学环节包括: 目标分析——知识建构——知识迁移——能力拓展——总结反思[2][3][4]. 实现转变的关键是如何设计问题链,在“例中学”与“做中学”中促学生层层深入学习. 以下,以“手拉手模型”为例,借助西蒙数学理论,探讨几何复习课的设计.

3.1 实践案例

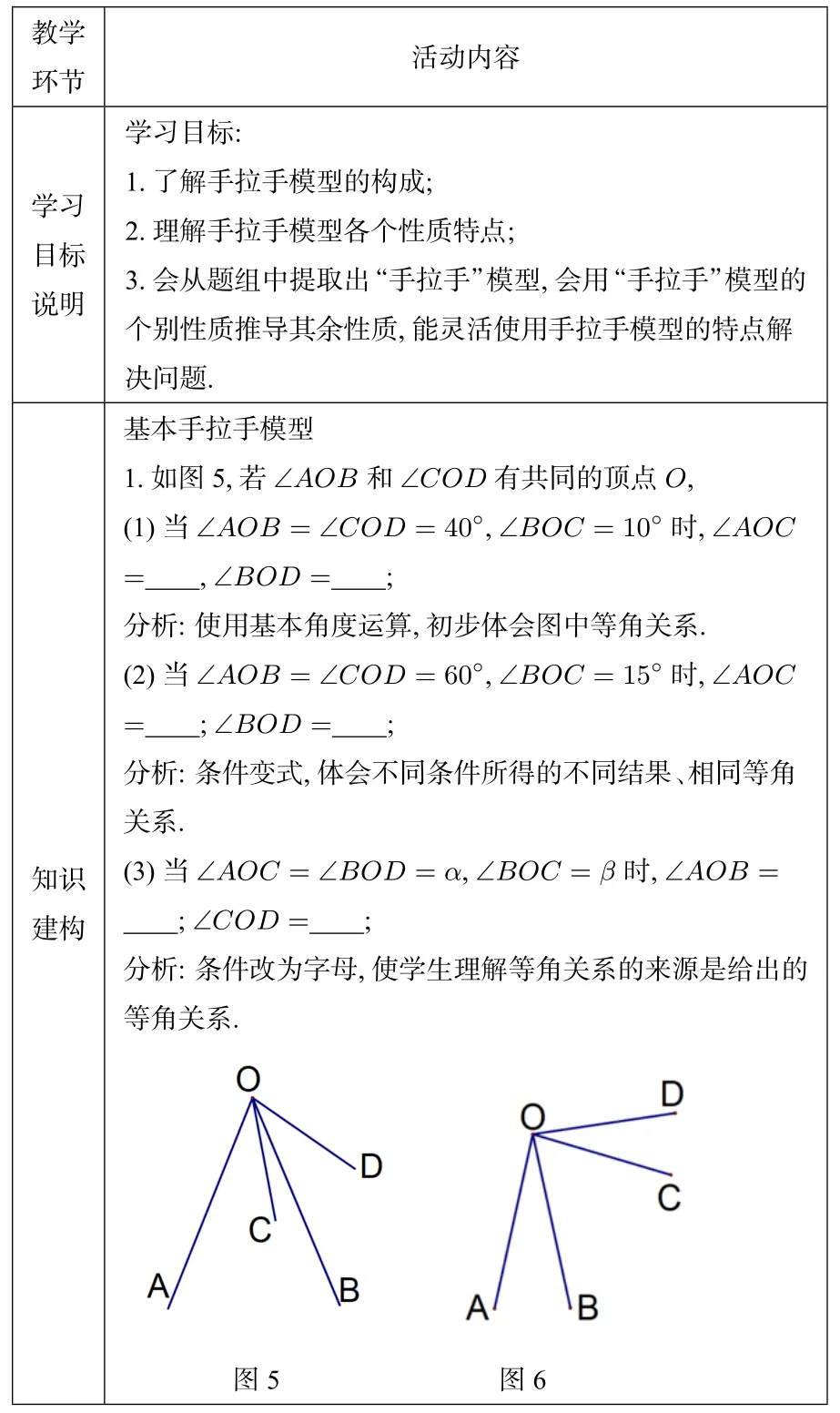
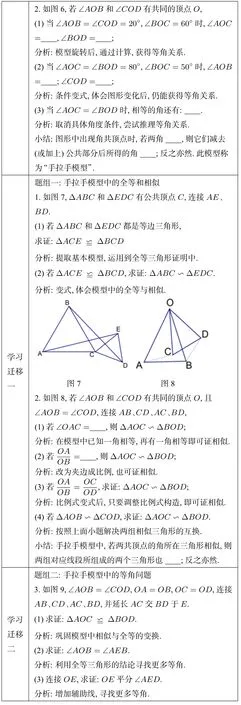
3.2 设计说明

首先,学习目标是了解模型的形成、特点与应用. 从两个共顶点的角,到两个共顶点的三角形,再增加连线,最后在复杂问题中抽象出手拉手模型. 这是本节课的主线.

其次,进行模型的构建过程. 把两个相等的角放到同一个顶点,给出不同的已知条件,求相同的等角关系. 知识构建起点较低,适合各层次学生,是后续题组的脚手架. 整个过程中,学生贯彻“做中学”.

第三,进行关键的题组解题. 从难易度考虑,设计两个题组. 贯彻变式训练,重视知识联系,对每个题组给出相关的策略分析,重视小结. 既保证“做中学”,也实现“例中学”.

第四,进行能力拓展. 这个部分选用了一道包含手拉手模型、中位线定理和圆中基本概念的综合题. 其中还需要添加辅助线,才能抽象出手拉手模型和中位线模型.

最后的反思,旨在反思解题策略和关键,加强课堂效果.

4 教学启示与反思

初三学生虽然具备一定的几何知识和相应的解题方法.但在分析、解决问题时仍需要适当的“脚手架”,对后进生而言尤为重要. 经过实践发现,问题的切入应从两个相等的角有共同顶点开始. 由于未涉及三角形,单纯使用角度的加减运算,这种“低起点”做法对所有学生均适用. 通过变换已知角度,计算出等角关系,从而引出手拉手模型. 再提出两个题组让学生进行探索,实现小步台阶、层层深入. 经过反思与求证,笔者有如下几点感悟:

(1)自适应产生式系统的形成,要体现学生的主体性

题组训练的主要内容总是围绕学生的需要来进行,按照学生的认知规律,由浅入深,逐步实现知识的迁移与巩固. 设计题组时,必须低起点,因材施教. 课堂中多肯定与激励,激发学生的内驱力,提高学生的学习主动性. 自适应产生式系统既要重视学生的学习主体地位,也要帮助学生紧跟课堂脚步,积极参与课堂训练,提高复习课效果,做到人人都有提高.

(2)数学产生式的主线,要保证几何模型的同一性

学生或许每题都能解决,但是否每题都能从中提取数学模型,则需要老师的引导与自我反思总结. 如果学生无法找出题组中的题目关系,则难以理解题组的小结内容. 产生式系统的效果,必须建立在知识系统化的基础上. 教师要强调题组中的数学模型在解题过程中的作用,要把同一几何模型贯穿课堂,从基本模型出发,到复杂的变式变形,适当引导学生把握每个产生式之间的联系,形成系统.

(3)数学模型的建构,要明确思考的指向性

几何模型的复习,除了明确模型的“前世与今生”,更要为学生指出将来要怎么使用数学模型. 如出现怎样的条件,就要使用哪个模型. 最直接的方法,就是给出问题拓展,利用一些真题进行训练,做到训练从严. 用同一个模型解决不同的问题,让思考方向更明确.

在以几何模型为主线的复习课中,以西蒙数学教学法重构教学流程,编排适当的“脚手架”,贯彻“做中学”和“例中学”,小步台阶、层层深入,可以有效提高复习效率.以“西蒙数学”的视角去设计认知工作单,改“重教”为“重学”,或能优化传统课堂的某种教学模式, 逐渐改变教师的角色特点,使学生在复习课堂中不再被动,而是自主进行知识的建构与学习反思.长此以往,学生的数学素养、学习能力的提升,就会渐见成效.