让问题摇动问题,让题干枝繁叶茂——一堂几何复习课的思考

广东省佛山市顺德区容桂街道四基中学(528305) 邱志刚

《义务教育数学课程标准(2011年版)》提出,学生掌握数学知识,不能依赖死记硬背,而应以理解为基础,并在知识的应用中不断巩固和深化. 为了帮助学生真正理解数学知识,教师应注重数学知识与学生生活经验的联系、与学生学科知识的联系,组织学生开展实验、操作、尝试等活动,引导学生进行观察、分析,抽象概况,运用知识进行判断. 教师还应揭示知识的数学实质及其体现的数学思想,帮助学生理清相关知识之间的区别和联系等. 根据学科的特点,让学生在应用中不断巩固和深化,让知识有“生长点”和“延伸点”,使学生能感受知识的结构和体系. 本文以人教版九年级上册“切线的证明与计算”复习课教学中,笔者借助基本构图,让题目不断生长,从而培养学生在经历题目的“生长”、“延伸”过程中感受到数学的整体性.

1 内容分析

本节内容是在前面学完“直线和圆的位置关系”后的一节知识总结复习课. 这节课包含着切线的判定以及利用切线的性质进证明和计算,既是学生刚学完圆的基本知识的一个总结又为后续学习“圆和圆的位置关系”奠定基础,是一节承上启下的复习课,同时,本节课内容在“圆”这一章中具有核心地位,体现在线和圆、图形和圆的关系,在中考中的比重也比较大.

它的重点内容主要包含切线的判定、切线的证明、切线的计算以及内切圆和画图. 以往教师在上数学复习课时容易形成一套思维定势: 概念、性质、定理的回忆;例题选讲1、2;配以一定比例的练习题;小测试反馈,导致复习课往往是教师一言堂、满堂灌. 但数学复习课绝不是对知识的简单重复,而是学生认知的继续、深化和提高. 事实上,上好复习课,对学生巩固学过的知识,为后面的学习打下良好基础,至关重要. 因此,本节课的设计是通过一道基础题不断生长,让学生在题目的生长过程中深化概念的认识、理解知识的运用和构建圆的模型.

2 学情分析

因为是复习课,学生在此之前已学习了“直线和圆的位置关系”,对基本概念、知识运用已有了一定的掌握,基本了解切线证明所需的条件,从复习前期的学生反馈来看,还有相当一部分学生对切线证明几种方式的运用还不太了解,对于应用勾股定理来进行切线的计算虽然有了初步的认识,但比较恐惧复杂图形下的问题. 九年级的学生已有了一定的抽象逻辑思维,因此,本节课从模型数学开始,通过题干的逐步生长让学生的思维随之而生长.

3 教学目标

①经历题目的生长,从中找到直线和圆的位置关系,并归纳出圆切线的几种判定方法;在生长过程中,通过实验、操作、尝试活动引导学生观察、分析和抽象概况.

②利用切线的性质进行线段和角的计算或论证并解决有关问题;

③通过知识的迁移,感受数学知识的价值和魅力,培养合作学习的意识和探索精神.

4 教学重、难点

重点: (1)归纳出圆的切线的几种判定方法; (2)利用切线的性质进行线段和角的计算或论证.

难点: 通过活动以及题目的生长了解知识的数学实质及其体现的数学思想.

5 教学过程

5.1 夯实基础、知识梳理

典例1: 如图1,AB 与⊙O 相切于点A, 已知OA = 3, AB = 4, 则OB =____.

图1

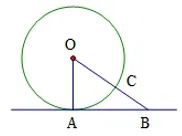
变式1: 如图2-1, AB 与⊙O 相切于点A, 若AB = 4, BC = 2, 则⊙O 的半径=____.

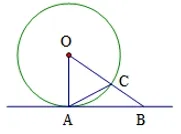
变式2: 如图2-2,AB 与⊙O 相切于点A,连接AC,如果OC =AC,则∠BAC =____.

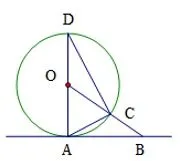
变式3: 如图2-3,上题条件不变,延长AO 交⊙O 于点D,连接CD,则∠D =____.

2-1

2-2

2-3

活动预设: 学生能较快速地完成例题和变形题,从解题的过程中能了解图形的结构和定义、性质以及相关联的知识.

设计说明: 传统的复习模式以知识的重现为主线,在本节课的知识梳理中,采用了问题式的训练,学生通过解决一个个问题得出相关的概念,从最简单的基本图形模型——圆背景下的直角三角形进行变式,用几何画板让学生感受图形的变换和生长,通过基础训练去复习切线的性质定理及应用,同时让学生用思维导图的方式进行知识梳理,让学生初步体会数学知识之间的联系和衔接,对后续题目的继续生长有一定的帮助.

5.2 归纳总结、脉络整理

活动预设: 学生通过对例题及变式题的训练,通过总结和归纳,小组把知识点利用思维导图的方式对所学的概念进行归纳和梳理,这块知识点先让学生进行预习作业,随后让小组推举学生上来展示和解释.

知识梳理:

设计说明: 通过学生画的思维导图把已学“圆和直线位置关系”的知识结构、知识脉络梳理得更清晰、清楚,课堂里再让各个小组对所画的思维导图进行整理和完善,让小组代表把完善修改后的思维导图进行展示. 目的旨在让学生进行不同画法的比较,以便取长补短让学生初步体会数学知识之间的紧密关系.

5.3 课堂探究、方法提炼

典例2.(变式3 的进一步变式)如图3,AD 是⊙O 的直径,C 是⊙O 上的一点,且∠D = ∠BAC. 求证: AB 是⊙O的切线.

图3

典例3.(典例1 变式)如图4,直线AB 与⊙O 相切与点A,OB 是∠ABE 的角平分线,那么直线BE 与⊙O 有怎样的位置关系? 为什么?

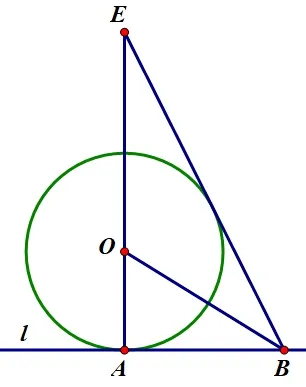
图4

(思考: 用典例1 的方法还能解决问题吗? 为什么? )

活动预设: 针对切线的证明有两种基本的方法,根据前面的问题进行改编,通过问题让学生去解决这两个问题,由于有了前面的知识梳理,学生对这两题的解决比较顺利,为下一步进行“切线”的基本方法打下基础.

设计说明: 前面学生已总结出了和线段有关的基本性质,在切线的证明中,采用学生课堂探究的方式,且和三角形具有特殊的位置关系—相切通过对前面习题的进一步变式,在变式中图形遵循由三角形和圆组成,两道题的证明方式既有知识的连贯性,又有思维的递进关系,让学生通过这两题的解决得出此类问题的基本方法是: 当线与圆有公共点时,用切线的性质“连半径,得垂直”,当线和圆没有明确告知公共点时可以尝试用“作垂直,求半径”的方法,在学生顺利解决问题后,通过问题驱动让学生自己去总结切线的证明方法.同时用思维导图的方式进行方法梳理和总结.

5.4 问题拓展、迁移应用

典例4.(典例1、2 变式)如图4-1,AD 是⊙O 的直径,AB切⊙O 于点A,连接OB,作CD//OB 交⊙O 于点C,BC 的延长线与AD 的延长线交于点E.

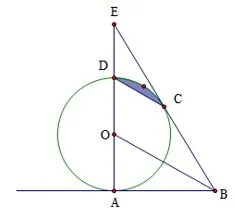
图4-1

(1)求证: BE 是⊙O 的切线;

(3) 在(2) 的条件下: ①求线段AB 的长? ②求阴影部分的面积? ③如图4-2, 连AC 交OB 于点F, 求证:∆OAF ～∆EBA.

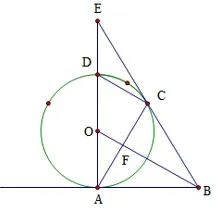
图4-2

(4)如图4-3,过点D 作DF//AB,交BE 于F 点,P 为优弧上一点,DF =1,AB =2,求tan ∠DPC 的值

图4-3

活动预设: 对典例1 继续进行变形, 其中1、2 问是往2018年黔三州中考题方向靠拢,第4 问是往2020年广东省中考题方向改编,前三个问一共有五个小问,这五个小问之前有比较大的联系,每个问题都是在前一个问题的基础上生长出来,对于学生解题的难度不会很大,但第4 问是在前面问题基础上进行增添或减少线段得到的,看似联系不广,但如果善于挖掘线段之间的关系,找到图形间的联系,两道题的难度对于学生而言会比较适当.

设计说明: 本题是典例1、2 的两个图形的整合,这样改编的好处是让学生进一步体会数学知识间的联系,学会融会贯通,在强化基础知识的同时,通过中考切线问题考试热点的讲解,提高学生对切线证明及切线计算问题的理解. 更为重要的是,学生通过题目的生长了解题目是如何由一个简单的图形变成繁复的图形, 如何由一个题干变成枝繁叶茂的“参天大树”,对学生克服复杂图形的恐惧有一定的帮助.

5.5 总结提升、课堂评测

典例5.如图5,AC 为⊙O的直径, B 为AC 延长线上一点,且∠BAD = ∠ABD =30◦, BC = 1, AD 为⊙O 的弦,连接DO 并延长交⊙O 于点E, 连接BE 交⊙O 于点M.

图5

(1)求证: 直线BD 是⊙O 的切线;

(2)求⊙O 的半径OD 的长;

(3)求阴影部分的面积;

(4)求线段BE 的长;

(5)求线段BM 的长;

设计说明: 一节课的效果如何,课后的习题评测也是必不可少,通过课堂的评测可以让教师及时了解学生对知识的掌握情况,适当调整教学顺序,如果课堂里没有时间再进行调整则通过检测出现的问题在下一节课中也可以进行反馈.同时,能够更好地为今后的教学设计提供改进的措施和方向.

6. 设计反思

6.1 问题驱动中整合知识之间的联系

知识网络的架构,打破以往学生背知识点的习惯,通过“问题驱动”的引出,使整个建构过程逻辑性更强,出现的更为顺畅和自然. 其目的是让学生在“数学问题”出发,保持学生的学习热情,这不至于让学生因为学过的知识,简单的背诵而显得索然无味,更关键的是注重知识间的逻辑结构. 其次是通过“问题解决”提炼模型、“问题变式”形成思想,找到解决模型的思想和方法,通过师生合作整理、整合出知识的脉络,找到知识间的内在联系,以此来实现归纳总结出本章主要的数学思想和方法. 最后用“问题拓展”让学生在学会用思辨的方式在前面构建好知识脉络、知识总结之后给出问题的解决.

6.2 问题生长中搭建知识之间的桥梁

以“问题”代替直接复习知识点,充分激发学生在数学复习课堂中的探究欲望,落实学生在数学复习课堂中的主体地位.学生通过亲身经历圆为模型下线之间关系的过程,主动构建圆切线的证明和计算的方法的知识网络. 同时,“问题”助推了师生互动与生生互动,学生不再是“静止”状态,而是积极主动地参与到教学活动中来. 通过问题的不断生长,学生初步掌握了切线、线段和面积之间的关系,为后续解决这些问题很好地搭建了一个桥梁. 所以教师在上复习课的时候,如果以“问题”代替直接复习知识点,引发学生积极主动地参与到教学活动中来,通过问题让学生自主归纳, 总结知识点和方法,让学生在思维中得到升华.

6.3 问题解决中促进知识之间的迁移

“义务教育数学课程标准”在7∼9年级的学段目标中提出: 让学生经历从不同角度寻求分析问题和解决问题的方法的过程,体验解决问题方法的多样性,掌握分析问题和解决问题的一些基本方法;在本节课里,学生通过系列“问题”掌握了切线证明方法和线段的计算,又通过“问题”的不断变式让学生体会建构好的知识脉络和相似、阴影部分的面积以及三角函数求解的知识迁移. 进一步加深对模型的理解,形成思想、凸显策略.

笔者认为,传统的复习课更多的是以一种知识重现、记忆和解题方法、策略的教授为主,对于学生来说,复习课就是一节习题课, 复习课上显得枯燥和乏味, 但本节课通过“问题”驱动“问题”中,学生的思维在不断深化,学生在复习课中能主动、轻松、愉快地学习并真正体悟到数学的内涵所在.