初中生直观想象素养的现状调查与培养策略*

山东省济南市济南大学数学科学学院(250022) 郭 蕾 刘星娟 靳绍礼

直观想象素养是《普通高中数学课程标准》中提出的六大数学核心素养之一,虽然在《义务教育数学课程标准》中没有明确提出培养初中生直观想象素养的要求,但是初中阶段作为高中的准备阶段,作为数学教育者在这个阶段也应该尽早地关注学生的几何直观能力,为培养其直观想象素养奠定坚实基础.

笔者通过文献梳理发现,当前学术界对直观想象素养的研究更多的是关注直观想象素养的内涵与结构、直观想象素养的培养、直观想象素养水平的现状调查、直观想象素养水平的评价等方面的研究. 其中,关于直观想象素养水平的评价研究有: 张和平基于TⅠMSS、PⅠSA 测试框架,利用因子分析法与专家评分法综合尝试构建了小学生几何直观能力测评模型: Y = 0.3A+0.3B+0.4C,其中,Y 代表“小学生几何直观能力”,符号A、B、C 分别代表形成图形的认识、利用图形描述问题、利用图形分析问题3 个指标[1];沈晓凯基于董林伟的研究,构建了高中生直观想象素养4 个水平的评价框架[2]. 根据以上文献梳理可见,对于学生直观想象素养的研究主要以评价和测量为主.

因此,本文利用编制的直观想象素养水平测试试卷,通过大样本对初中生直观想象素养水平现状进行研究,以期为初中生直观想象素养水平的提升提供可行策略.

1 理论基础

1.1 直观想象素养的内涵与价值

中国教育部2014年在《关于全面深化课程改革落实以德治国根本任务的意见》中正式提出“核心素养体系”的概念[3]. 数学学科核心素养是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现. 数学学科核心素养包括: 数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析六个方面[4].

直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式理解和解决数学问题的素养. 其主要表现为: 建立形与数的联系,利用几何图形描述问题,借助几何直观理解问题,运用空间想象认识事物[5]. 直观想象是发现、提出、分析和解决问题的重要手段,是探索和形成论证思路、构建抽象结构的思维基础.

因此,提高初中生的几何直观能力和直观想象素养,能为培养其在高中阶段的直观想象素养起到很好的奠基作用,对提高其高中数学思维和理解能力及数学成绩都有一定意义.

1.2 直观想象素养的评价理念

《普通高中数学课程标准(2017年版)》将直观想象水平分别从情境与问题、知识与技能、思维与表达、交流与反思4个维度划分为3 个水平. 并强调: 对直观想象素养的评价,应该以课程目标、学业质量标准为依据,注意阶段性、连续性与整体性,结合教学内容,通过创设合适的情境,围绕直观想象素养4 个方面的主要表现进行评价: 建立形与数的联系、利用几何图形描述问题、借助几何直观理解问题、运用空间想象认识事物.

1.3 Van Hiele 理论

20 世纪50年代,荷兰教师Van Hiele 夫妇将几何思维划分为五个水平: 视觉(visuality)、分析(analysis)、非形式化的演绎(informal deduction)、形式化的演绎(formal deduction)、严密性(rigor)[6]. Van Hiele 夫妇提出的几何思维五水平理论和建立的几何思维水平体系[7-8],对后世的对学生的几何思维水平及直观想象素养水平的研究有十分重要的意义,本文的测试卷编制及水平划分过程中均充分借鉴了该理论和体系.

2 研究设计

2.1 研究对象

初本文选择济南市某中学的初二学生为研究对象,共计发放测试卷290 份,去除空白卷等无效测试卷后,累计收回280 份测试卷. 其中,女生测试卷129 份,男生测试卷151 份.测试卷主要包括了基本信息、素养测试两个部分. 采用《普通高中数学课程标准(2017年版)》中给出的评价理念来评价学生的直观想象素养水平.

其一,基本信息,主要包括学生的班级、性别、期中考试数学成绩等背景信息,通过这些调查,对初二学生的直观想象素养水平的差异性和相关性做横向和纵向的比较研究. 其二,素养测试,该部分包括14 个大题,共计18 个小题,编号形式为: 大题号(小题号),如12(1),指的是第十二大题第一小题. 将18 个小题分为三个水平,其中1、2、4、11、12(1)、14(1)属于水平一,难度较低,3、5、6、8、12(2)、13(1)、14(2)属于水平二,难度中等,7、9、10、13(2)、14(3)属于水平三,难度较高,18 个小题从不同方面考察学生数形结合和直观想象水平.

2.2 初中生直观想象素养测试量表信度、效度、难度、区分度分析

2.2.1 信度分析

信度即测验结果可信的程度,它是反映测验结果可靠性及稳定性程度的指标. 如果测验题目包含主观性试题,且没有严格的评分标准,那么在估计这种类型的测验题目的信度时通常采用克伦巴赫系数来表示,本文中就选择克伦巴赫系数来表示直观想象素养水平测试卷的信度.

将收回的280 份测试卷基于标准答案和评分标准进行严格批改,根据最终成绩对测试卷进行信度检验,检验结果见表1.

表1 信度分析表

表1 显示,克伦巴赫系数为0.860,大于0.8,所以此测试卷的信度是在可以接受的范围内的.

2.2.2 效度分析

内容效度是指测验内容与预定要测的内容之间的一致程度. 本测试卷的题目来自八年级某次区统考的测试题,题目质量较高,且内容维度和题型以及每个题目所能达到的水平的确定都经过了反复推敲,内容效度较好.

结构效度的检验可以采用主成分因子分析,本文采用了KMO 检验和Bartlett 球形检验来检验测试卷的结构效度,检验结果见表2.

由表2 可知,根据Kaiser 的观点,KMO 值大于0.8 是比较好的,本测试卷的KMO 值为0.840,大于0.8,且p < 0.05,所以该测试卷整体效度较好.

表2 KMO 检验和Bartlett’s 球形检验的结果

2.2.3 难度分析

难度是指测试题目的难易程度. 难度的计算分客观性试题和主观性试题两种情况, 本测试题中1-10 题为客观性试题,11-14 题为主观性题目. 难度值与试题实际的难易程度成反比,通过Excel 分别计算每题难度,得到结果如图1.

图1

2.2.4 区分度分析

区分度是指测试题对不同考生的知识、能力水平的鉴别程度. 区分度的计算也分客观性试题和主观性试题两种情况,本测试题中1-10 题为客观性试题,11-14 题为主观性题目. 通过Excel 分别计算每题区分度,得到结果如图2.

图2

根据区分度的评价标准,给出测试卷中各题目区分度的评价结果,如表3.

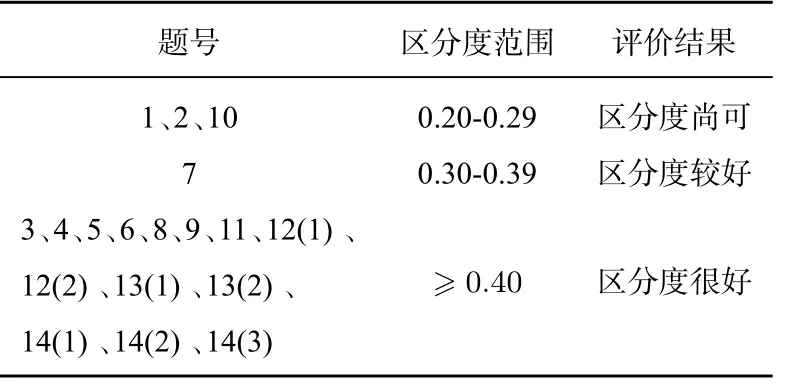
表3 各题区分度评价结果

3 数据的处理与分析

3.1 学生整体情况分析

在进行完对测试卷的信度、效度、难度、区分度分析之后,对学生在各个水平题目的得分进行统计,把该水平总分的60%视为该水平的临界分. 若学生的各个水平总分均达不到该水平的临界分,则认为该学生几乎不具备直观想象素养水平,若学生在某个水平上的总分可以达到该水平的临界分,则认为该学生达到了该水平,学生的直观想象素养水平以其能达到的最高水平为准. 其中水平一总分为24,临界分为14.1,水平二总分为30,临界分为18,水平三总分为24,临界分为14.4. 图3 给出了各水平人数百分比分布图.

图3

由各水平人数百分比分布图可见,只有极少数学生的直观想象素养水平可以达到水平三,有将近的学生的直观想象素养水平处于水平一和水平二,还有将近的学生几乎不具备直观想象素养水平.

3.2 各水平的基本情况分析

3.2.1 直观想象素养水平一的基本情况分析

对直观想象素养水平一的题目的得分情况做描述统计,得到表4.

表4 直观想象素养水平一描述统计

水平一满分为24 分,临界分为14.4 分. 由表可以看到,平均分为19.15 分. 平均水平可以达到临界分,但标准差为5.867 分比较大,说明在水平一的题目上学生的水平尚能达到较高水平,但得分差距比较大.

3.2.2 直观想象素养水平二的基本情况分析

对直观想象素养水平二的题目的得分情况做描述统计,得到表5.

表5 直观想象素养水平二描述统计

水平二满分为30 分,临界分为18 分. 由表可以看到,平均分为17.47 分,没有达到临界分,说明已经有部分学生的直观想象素养达不到水平二,且标准差为8.030 比较大,说明在水平二的题目上学生的得分差距比较大.

3.2.3 直观想象素养水平三的基本情况分析

对直观想象素养水平三的题目的得分情况做描述统计,得到表6.

表6 直观想象素养水平三描述统计

水平三满分为24 分,临界分为14. 4 分. 由表可以看到,平均分为4.31 分,与临界分相差较大,说明绝大部分学生的直观想象素养水平达不到水平三.

3.3 不同性别学生直观想象素养水平的差异性分析

3.3.1 直观想象素养水平总得分的性别差异性分析

首先对总成绩进行按性别分类的探索分析,得到的结果如表7.

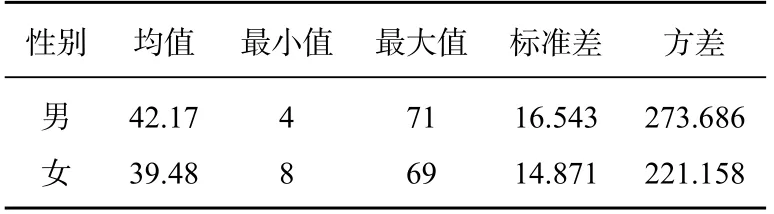
表7 对总分按性别进行探索分析结果

由上表可以看出,男女生总成绩的均值分别为42.17 分和39.48 分,相差2.69 分,说明男女生的直观想象素养水平在平均水平上有一定差异,女生的直观想象素养水平略低于男生. 但男生总成绩的标准差为16.543,女生总成绩的标准差为14.871,男生总成绩的标准差大于女生,说明男生直观想象素养水平的内部差异性更大.

为了更好地说明直观想象素养水平在性别之间的差异性,下面对总成绩得分进行独立样本t 检验,得到的结果如表8.

表8 独立样本t 检验结果表

根据性别分类的独立样本t 检验结果显示,方差齐性检验不显著(p > 0.05),即两组独立样本的方差是齐性的. 又因为均值t 检验中p = 0.157 > 0.05,所以两组样本之间没有显著性差异,即直观想象素养水平总成绩得分在性别间的差异不显著.

3.3.2 直观想象素养在不同水平维度上的性别差异性分析

首先对各水平维度的得分进行根据性别分类的探索分析,得到的结果如表9.

表9 对各水平维度得分按性别进行探索分析

分析表中结果可知,从均值上来看,水平一、水平二、水平三中男生得分的均值均大于女生,这说明男生在直观想象素养水平各方面上的表现都优于女生; 但从标准差上来看,水平一、水平二、水平三中男生得分的标准差也都大于女生,这说明男生在直观想象素养各水平上的个体差异性比女生要大.

为了进一步说明直观想象素养水平在不同水平维度上有没有显著差异,下面对各水平维度做按性别分类的独立样本t 检验,得到的结果如表10.

表10 不同水平维度按性别分类的独立样本t 检验结果

分析以上结果可知, 在水平一上, 两样本方差齐性检验不显著(p = 0.987 > 0.05), 即两组的方差齐性, 又因为均值t 检验中p = 0.529 > 0.05, 所以男生成绩优于女生,不存在显著差异;在水平二上,两样本方差齐性检验不显著(p=0.117>0.05),即两组的方差齐性,又因为均值t 检验中p=0.281>0.05,所以男生成绩优于女生,不存在显著差异;在水平三上,两样本方差齐性检验显著(p = 0.018 < 0.05),即两组的方差不齐,又因为均值t 检验中p = 0.015 < 0.05,所以男生成绩明显优于女生.

3.4 学生的直观想象素养水平与数学成绩的相关性分析

本部分采用Pearson 相关分析法分析直观想象素养水平与数学成绩之间的相关性,得到的结果如表11.

表11 直观想象素养与数学成绩的Pearson 相关分析结果

由表可知, 数学成绩与直观想象水平的相关系数为0.958,且p < 0.05;数学成绩与直观想象水平一的相关系数为0.903,且p < 0.05;数学成绩与直观想象水平二的相关系数为0.910,且p < 0.05;数学成绩与直观想象水平的相关系数为0.613,且p < 0.05. 分析如上结果可得: 数学成绩与直观想象水平、直观想象水平一、直观想象水平二存在非常高的正相关关系,与直观想象水平三存在较高的正相关关系.

因此在平常的教学过程中,教师应注重培养学生的直观想象素养水平,这不仅有利于提高学生的数学核心素养,对学生数学成绩的提高也有重要作用.

4 初中生直观想象素养的培养策略

4.1 构造数与形之间的联系,培养学生的数形结合思想

“数”是抽象的,“形”是直观的,而数学是数与形的统一,因此让学生直观地认识到数与形之间的关系,培养学生的数形结合思想在数学教育中尤为重要.

在教学过程中,教师可以将一些抽象的数学知识以直观的方式展现在学生面前. 比如,在学习函数的概念和图象时,给出一些实际生活中一个量随另一个量发生变化的例子,比如行星在宇宙中的位置随时间而变化, 气温随海拔而变化,树高随树龄而变化,给出这些现象的相关图片并展示出它们的变化规律,教师尝试用函数图象的变化来给学生解释函数解析式的含义,将给出的实际情境、函数解析式和函数图象结合起来,这样既可以激发学生的学习兴趣,又可以培养学生的数形结合思想,从而提高学生的直观想象素养.

通过观察教师给出的直观图象,在教师的引导下探索数与形之间的联系,形成数形结合的思想,对培养初中生的直观想象能力有着重要作用.

4.2 在难度水平比较高的题目上,对男女生实行分别教学

初中阶段的学生处于各方面能力快速增长的阶段,从传统观念来说,人们通常认为男生的几何直观和空间想象能力高于女生,通过本文的数据分析结果来看,这一现象仅体现在水平三即难度水平比较高的题目上,针对这一现象,本文拟提出一种在高难度水平题目上对男女生进行分别教学的策略.

较低水平的题目考察的是学生基础知识的掌握水平,对学生思维能力的要求不高, 但在面对高难度水平的题目时,女生几何直观和空间想象思维能力相对于男生的劣势就显现出来了. 因此在平时的教学过程中,为了实现男女生的均衡发展, 在高难度水平的题目方面应给予女生更多的关注.在教学中面对这一类题目时,应当更加关注女生,给予女生更多的指导,并设法将其所面对的问题更加具体化、直观化,充分利用女生更倾向于感性思维的特点,使其能在一个相对更加直观的情境下去理解问题,解决问题,从而提高女生在这一方面的思维水平,提高女生的直观想象素养水平;对于程度较好的男生则只需要给他们讲清楚题目所用到的原理,给他们更多的自己思考的空间,他们就可以充分利用自己的几何直观和空间想象能力,在自主探究的过程中,男生的直观想象素养水平就会得到很大程度的提高.

因此,笔者认为,在培养初中生直观想象素养时对男女生采用不同的教学方法是十分有必要的,这样既能充分提高女生的直观想象素养水平,又能在男生提高自身直观想象素养水平的同时提高自主探究能力,从而能同时提高男女生的数学成绩.

4.3 通过“几何画板”创设直观情境,提高学生的直观观察能力

随着科技的不断发展进步,多媒体技术在数学教学中的优点越来越明显,“几何画板”作为技术发展成果下的计算机辅助教学软件,在数学教学过程中体现出来的优势也越来越明显,正逐渐得到越来越广泛的应用.“几何画板”可以将以往传统的静态数学教学和徒手作图方式转变为借助辅助教学软件进行动态作图从而实现动态教学,引导学生在直观视觉观察的基础上对图形进行更加直观的认识.

教师在几何或者函数教学过程中应当注意将知识的讲解与“几何画板”的作图相结合, 这样既能吸引学生的注意力,又能激发学生的学习兴趣,加深学生对知识的理解. 比如在学习全等三角形的判定时,人教版教材给出了“探究三角形全等的条件”的信息技术应用环节,教师便可以充分利用这一环节,引导学生利用几何画板软件按照教材上的方法独立构造三角形,自主探究三角形全等的条件. 学生在独立操作的过程中可以更清晰地了解图形构造的过程,丰富自己的思维内容,提高自己的直观想象素养.

运用技术手段进行数学问题的研究探索,能把抽象的数学转化为具体的图形,使课堂生动化,增进学生的理解和记忆[9]. 因此在几何和函数教学的过程中,教师应尽量多地给予学生动手实践、自主探究的机会,帮助学生提高直观想象素养.