斜交型立体交叉隧道的地震动力响应研究
2021-02-24吴红刚孟庆一何长江李德柱
雷 浩, 吴红刚, 孟庆一, 何长江, 李德柱
(1. 兰州交通大学土木工程学院, 甘肃 兰州 730070; 2. 中铁西北科学研究院有限公司, 甘肃 兰州 730070; 3. 中铁九局集团有限公司大连分公司, 辽宁 大连 116031)
0 引言
由于受到围岩的约束,在地震作用下隧道及地下工程的动力响应较其他结构而言存在较大差异[1]。许多大地震发生后,对大量隧道结构造成了不同程度的损坏,众多学者对隧道工程在地震荷载作用下的动力响应问题有不同的见解[2-4]。立体交叉隧道由于其特殊性,在地震荷载作用下同一时刻往往受到入射、反射、绕射等多种地震波的相互影响[5],发生地震破坏时将会影响整条线路。因此,对立体交叉隧道在地震荷载下的动力响应进行研究显得尤为重要。
在隧道结构的抗震性能研究中,国内外学者目前主要集中于单线隧道及地铁隧道的动力响应[6-12],而对于立体交叉隧道的动力响应研究较少,且研究手段以理论分析及数值模拟为主。在数值模拟方面,文献[13-14]采用有限单元法和Newmark直接积分法分别研究了在浅埋及软土地基中立体交叉隧道的地震动力响应,结果表明立体交叉隧道中最大变形量及加速度都出现在上部隧道拱顶位置处; 朱正国等[15]对影响交叉隧道动力响应的不同因素进行研究,通过数值模拟得到地震作用对交叉隧道影响敏感性大小依次为围岩级别、隧道净距和隧道埋深。在关于立体交叉隧道振动台试验方面,Chen等[16]采用石膏隧道模型对重叠隧道开展了大型的振动台试验,试验结果表明隧道模型结构两侧的峰值应变和损伤程度沿高度呈“S”形分布,此外地震反应在隧道各部位均表现出显著的空间效应; 牌立芳等[17]对立体交叉隧道的地震动力响应特性进行了初步分析,得到了立体交叉下穿隧道的加速度和应变响应,研究结果表明隧道拱顶为地震荷载作用下的薄弱环节。
当前对于立体交叉隧道的研究在理论分析及数值模拟方面较为广泛,而开展试验较少,同时针对立体交叉隧道在地震荷载作用下的动力响应特性研究还未取得实质性突破[18]。因此,为了研究立体交叉隧道的动力响应,通过大型振动台试验,在加载X单向及XZ双向El-Centro波时,对斜交型立体隧道中上跨和下穿隧道及交叉区段坡体内部加速度峰值的分布规律进行研究,以期为此类立体交叉隧道的抗震设计提供基础试验参考。
1 试验设计
1.1 工程背景
盘道岭隧道[19]位于辽宁省丹东市振兴区,全长4 870 m,为单线隧道,隧道内埋深17~106 m; 草莓沟1#隧道位于辽宁省丹东市草莓沟村,全长3 205 m,为单洞双线隧道,洞身最大埋深约105 m。草莓沟1#隧道在DK250+865~+915处上跨盘道岭隧道,相交处轨面高差为14.19 m,结构净距为4.24 m,其交叉段空间位置如图1所示。

图1 立体交叉隧道示意图
通过TRT6000超前地质探测器来预测交叉影响区的地质条件,发现交叉区段围岩主要由不同风化程度的混合花岗岩组成,节理裂隙发育,岩体呈碎块状及块状。围岩中的波速vs为1 000 m/s,vp为2 600 m/s,根据相关围岩划分标准交叉区段围岩为Ⅳ级围岩。根据GB 18306—2015《中国地震动参数区划图》,场地区域属于Ⅶ级基本地震烈度范围内,可能发生破坏性地震。因此,对该场地进行相应的地震响应模型试验是十分有必要的。
1.2 相似关系设计
本次振动台试验综合考虑隧道埋深、断面尺寸及振动台尺寸等,并结合结构在地震作用下应考虑的相关参数,分别取长度、密度、弹性模量的相似参数Cl=1/50、Cρ=1/1.0、CE=1/30为基本参数。根据相似原理可以推导出其他相似关系[20],具体推导如表1所示。
1.3 相似材料配比正交设计
对于围岩相似材料的选择,参考丁祖德等[21]对Ⅳ级围岩相似材料的研究,并考虑实际材料的经济性及可行性,本次试验以Ⅳ级围岩为例,材料主要选取水泥、粗砂、水、土等。采用正交试验设计方法及室内试验[22],为了提高效率每次只进行单一参量的改变,共设计了5组配比试验,具体配比及其力学参数如表2所示。
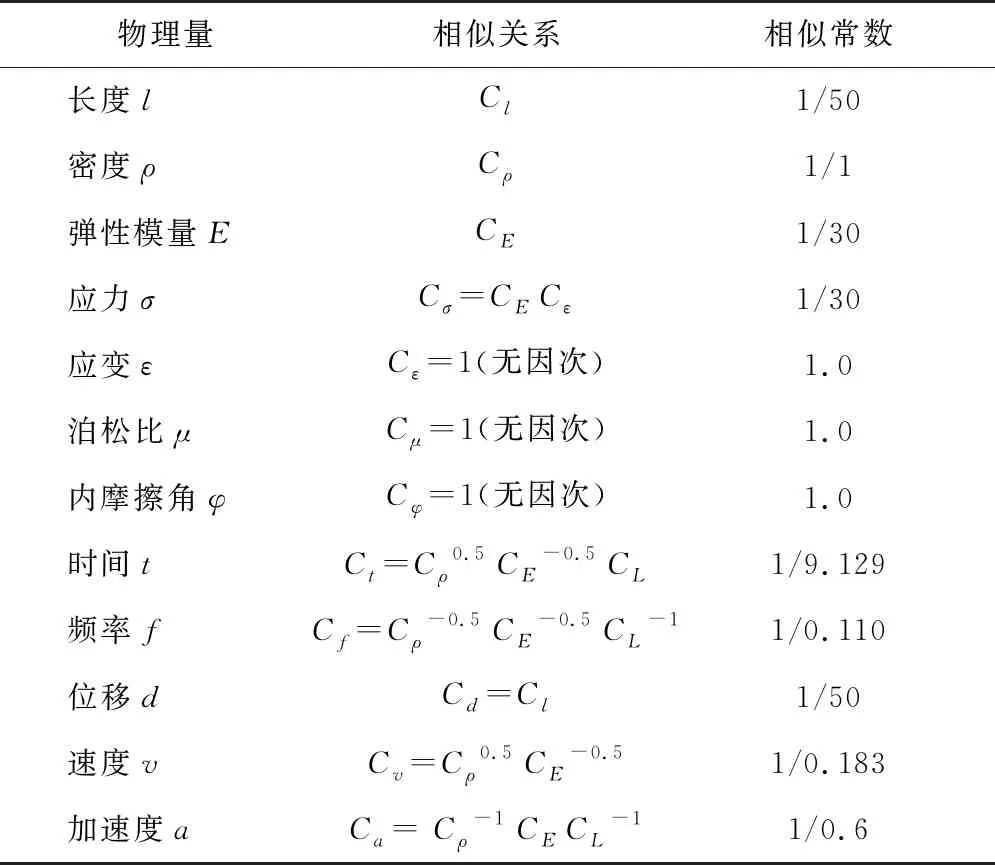
表1 相似参数设计
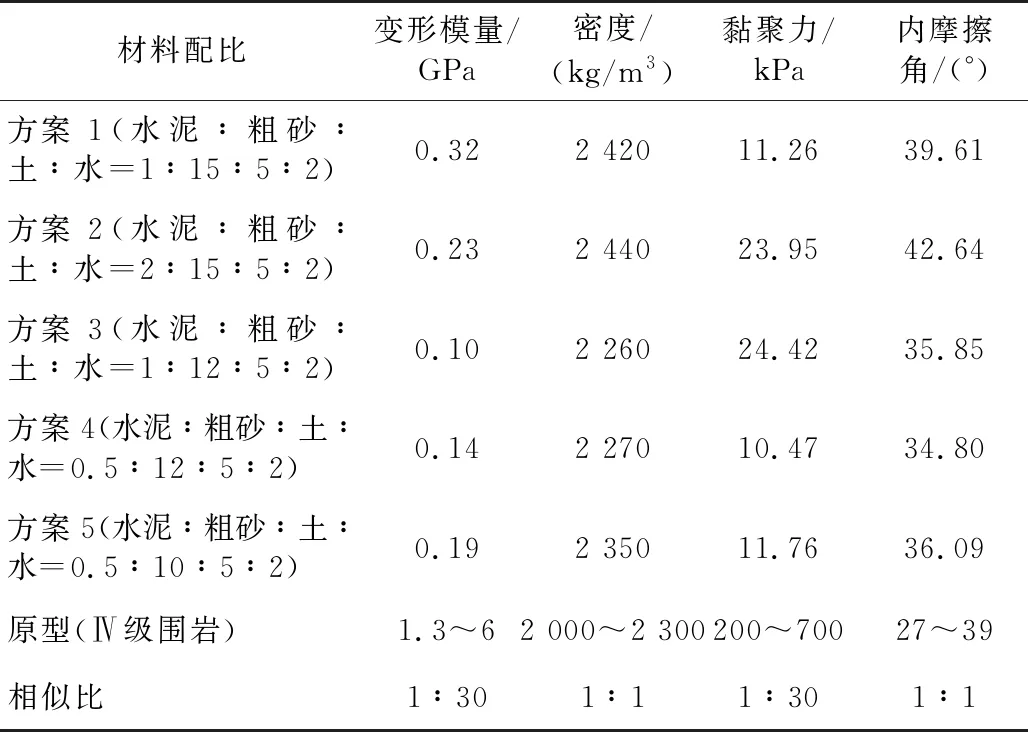
表2 相似材料配比正交设计
经过上述正交试验及相似换算,可以看出方案4(水泥∶粗砂∶土∶水=0.5∶12∶5∶2)相似材料的变形模量E、黏聚力c、内摩擦角φ及密度ρ等都满足Ⅳ级围岩的相似比; 另外采用石膏∶石英砂∶水=1∶1.5∶2来模拟隧道衬砌,其相似关系也都满足相似设计。
1.4 模型设计
本次振动台试验在甘肃省地震局黄土地震工程实验室进行,实验室采用VPS-600ES-2双向(X向、Z向)振动台,振动台尺寸为4 m×6 m,最大负荷量为250 kN,工作频率为0.1~50.0 Hz,最大位移X向为250 mm,Z向为100 mm,如图2所示。

图2 振动台系统
为了同时分析不同交叉形式立体隧道的响应,试验设计为左右2幅,左幅为正交型立体交叉隧道,右幅为斜交型立体交叉隧道。本文仅对右幅斜交型立体交叉隧道进行分析,左幅立体交叉隧道响应将在其他文章进行叙述。
试验中将隧道模型的初期支护与二次衬砌视作整体结构(下文简称衬砌结构),同时在隧道洞口两端分别放置1层厚30 mm聚苯乙烯塑料泡沫板,用以消除箱体侧壁的约束,以防隧道由于箱体原因而产生振动。隧道模型如图3(a)所示。
振动台模型箱是由有机玻璃、U型钢及聚苯乙烯塑料泡沫板组成顶面敞开的可视化箱体,设计尺寸为2.8 m×1.4 m×1.8 m,如图3(b)所示。为了减小试验中模型的边界效应,采取了以下措施: 1)在模型箱水平振动方向两侧内壁加1层50 mm厚的高强度聚苯乙烯塑料泡沫板以减小振动波的反射; 2)为减少模型箱侧壁摩擦,在试验箱两侧均匀涂抹凡士林并在箱底铺设粗砂材料,将其处理成摩擦边界,以减小箱底和土体的相对位移。经过验证,模型箱的边界效应基本在可接受误差范围内。布置完成的试验模型如图3(c)所示。两隧道空间中以小角度斜交,交角为20°,根据几何相似比1∶50,模型中两隧道的净间距为8 cm。为了便于叙述,下文将草莓沟1#隧道称为上跨隧道,盘道岭隧道称为下穿隧道。
1.5 测试断面及传感器布置
本次试验主要研究模型箱右幅斜交型立体交叉隧道影响区段、围岩及坡体内部的动力响应特性,所以主要在隧道拱顶及仰拱轴向、两隧道交叉影响段及坡体内部共布设16个加速度传感器。具体加速度传感器布设方式(见图4)如下:
1)分别以上跨和下穿隧道交叉中线断面的拱顶及仰拱为中心,沿轴向在中心及两侧各布设1个加速度传感器,其布设间距取30 cm(上跨及下穿隧道分别以SA和XA编号,且交叉中心断面为Ⅰ、Ⅰ′,影响区段两侧断面为Ⅱ、Ⅲ及Ⅱ′、Ⅲ′)。
2)在两隧道交叉段中线位置沿竖向布置1个加速度传感器,由于2隧道净间距为8 cm,此处传感器间距取4 cm。
3)在上跨隧道拱顶沿交叉中心断面竖向布设2个加速度传感器,下穿隧道仰拱底沿交叉中心断面竖向布设1个加速度传感器,为了与隧道交叉段形成对比,此处布设间取10 cm(交叉段及坡体内部以PA编号)。

(a) 隧道模型
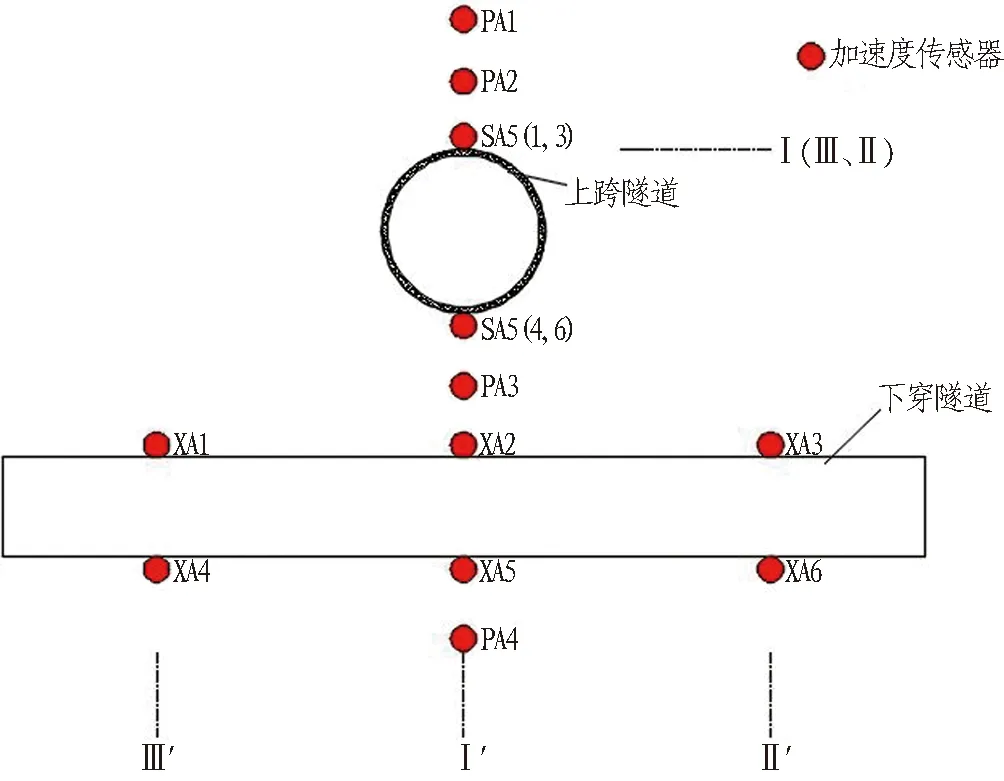
(a) 传感器布置方式
1.6 加载工况设计
试验中主要输入的地震波为正弦波及El-Centro波,加载方向主要为X向(水平向)及XZ双向耦合(水平-竖直双向)。对其台面所输入的El-Centro波进行0.5~40 Hz带通滤波后,其地震波的加速度时程曲线如图5所示。同时在试验开始前、结束后及每次改变输入地震波幅值大小时,都输入0.05g的正弦波进行扫频来测试系统的动力响应情况[23]。加载工况如图6所示。
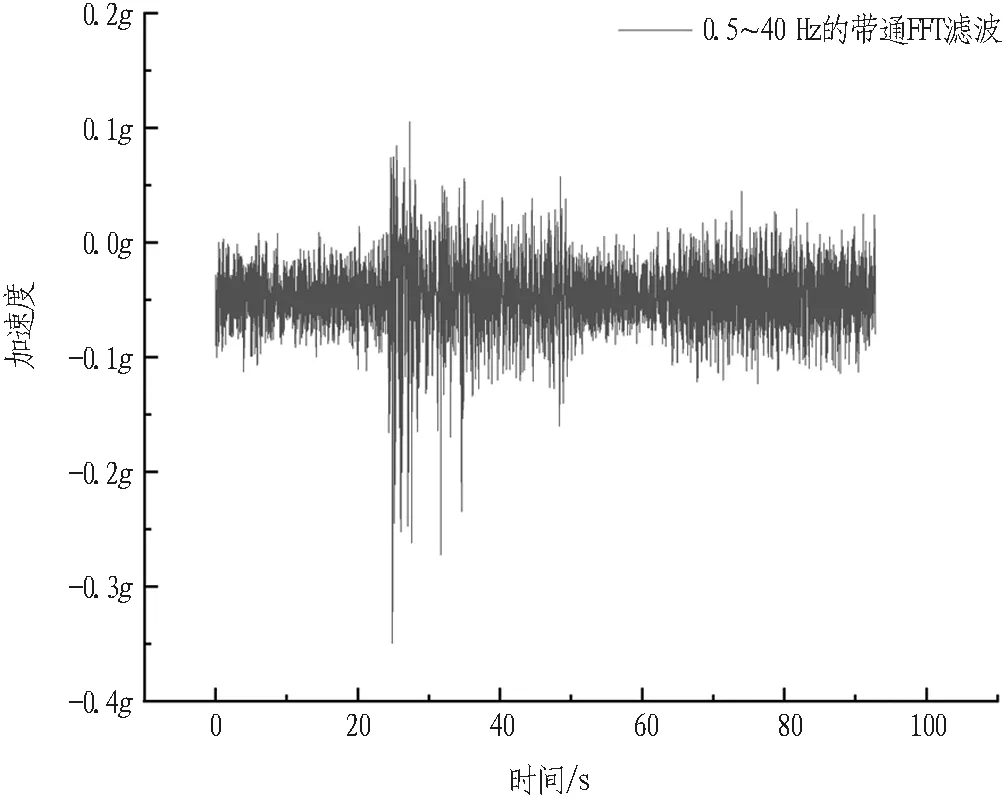
图5 El-Centro波加速度时程曲线
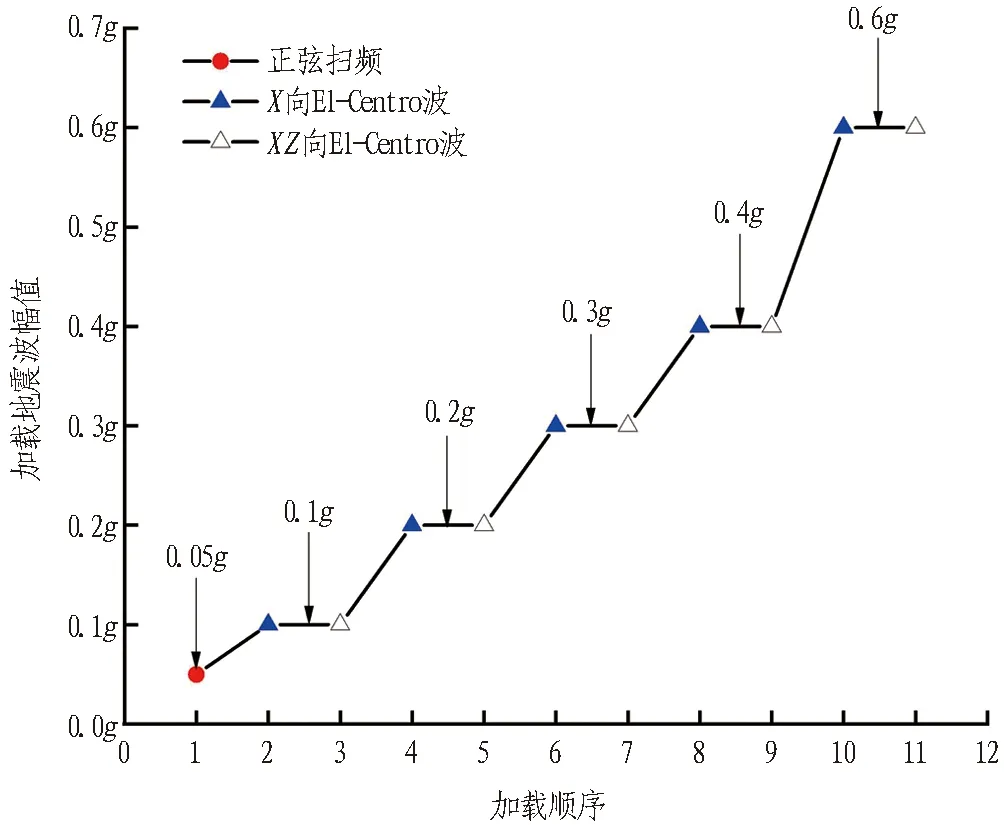
图6 地震波加载工况图
2 试验结果分析
2.1 X向加载时加速度峰值分析
2.1.1 上跨隧道加速度峰值分布
在加载X向El-Centro波时,为了对比隧道拱顶及仰拱轴向加速度在同一工况下的不同动力响应,将拱顶及仰拱结果绘制在同一图中。其中下轴及上轴分别表示仰拱及拱顶的测试断面位置,而左轴及右轴分别为仰拱及拱顶的加速度峰值分布,绘制其加速度峰值分布,如图7所示。
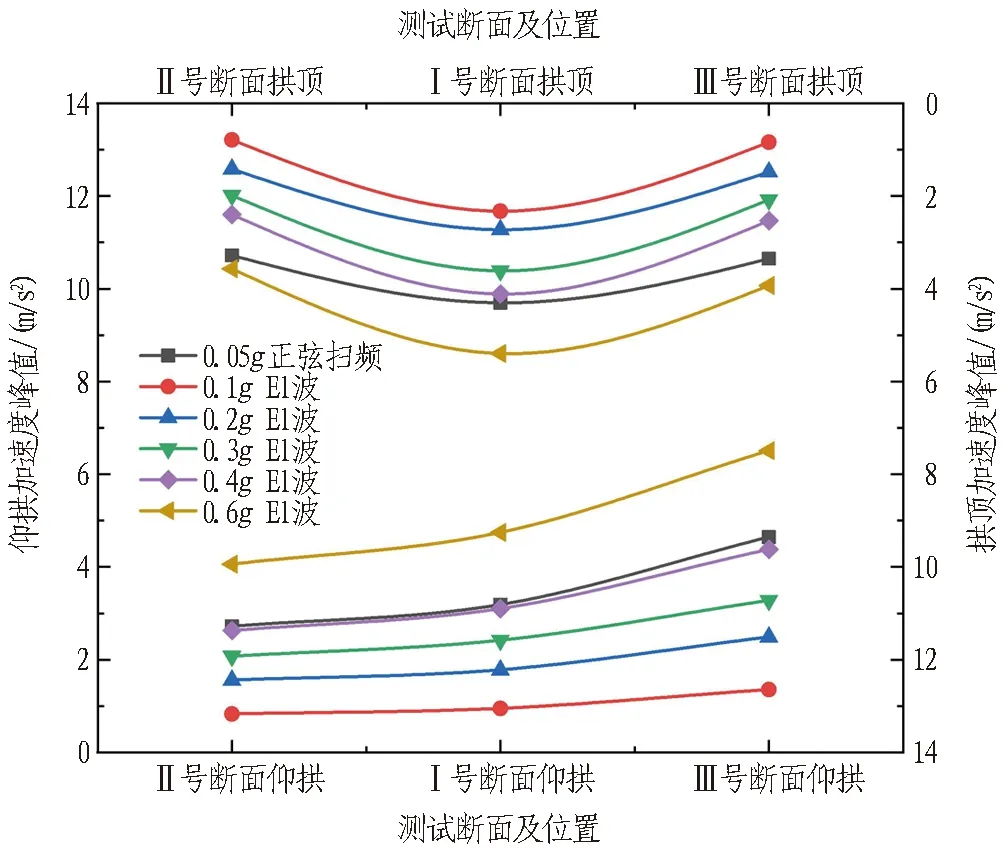
图7 X向上跨隧道加速度峰值分布
由图7可知,上跨隧道轴向加速度峰值分布及变化呈现出一定的规律性: 随着加载工况的增大,各测试断面位置处的加速度峰值随之增大; 对于上跨隧道拱顶,交叉段中心Ⅰ号断面处加速度峰值最大,影响区段两侧Ⅱ、Ⅲ号断面加速度峰值基本相等,近似呈“抛物线”分布; 而对于上跨隧道仰拱,交叉段中心Ⅰ号断面处加速度峰值减小,其大小依次为: Ⅱ号断面<Ⅰ号断面<Ⅲ号断面,近似呈“斜直线”分布; 同时也可以看出,Ⅰ号断面仰拱处加速度峰值明显小于拱顶处,较其他2个断面变化较大。以0.4gEl波工况为例,Ⅰ号断面拱顶峰值加速度为仰拱处的1.43倍,而Ⅱ、Ⅲ号断面拱顶峰值加速度分别为仰拱处的91%、95%。这是由于上跨隧道埋深较浅,拱顶对地震波的吸收较少,其加速度响应较为强烈; 而隧道仰拱由于下穿隧道的存在,使土体挤压,使仰拱处土体更为紧密,从而对地震波吸收明显,使仰拱处的加速度有明显减小。
为了更加明显地表达不同工况下隧道拱顶及仰拱的变化趋势,以0.1gEl波工况为基准,分析其他工况下的加速度放大系数,其中0.1gEl波工况下Ⅰ、Ⅱ、Ⅲ号断面拱顶(仰拱)的加速度峰值分别为2.33、0.79、0.84 m/s2(0.95、0.83、1.36 m/s2),结果如图8所示。由图8可以看出,拱顶处各个断面加速度峰值随加载工况变化较为敏感,容易成为整条线路的抗震薄弱环节; 而仰拱处各个断面的变化较为平稳,且在0.2g~0.4g加速度放大效应增幅较小,加速度放大系数最大为2.55,而在0.4g以后其放大系数出现了明显的突增,最大达5.01。
由于交叉区段为重点研究对象,所以同时也分析了交叉段中心Ⅰ号断面仰拱处(SA5测点)在不同加载工况下的加速度时程曲线,如图9所示。通过时程曲线也可以看出,随着加载El波幅值的增大,上跨隧道仰拱处加速度响应越强烈。在加载0.1g~0.6gEl波时,其峰值加速度分别为0.95、1.78、2.39、3.06、4.75 m/s2,且加速度峰值基本出现在加载后20~40 s。
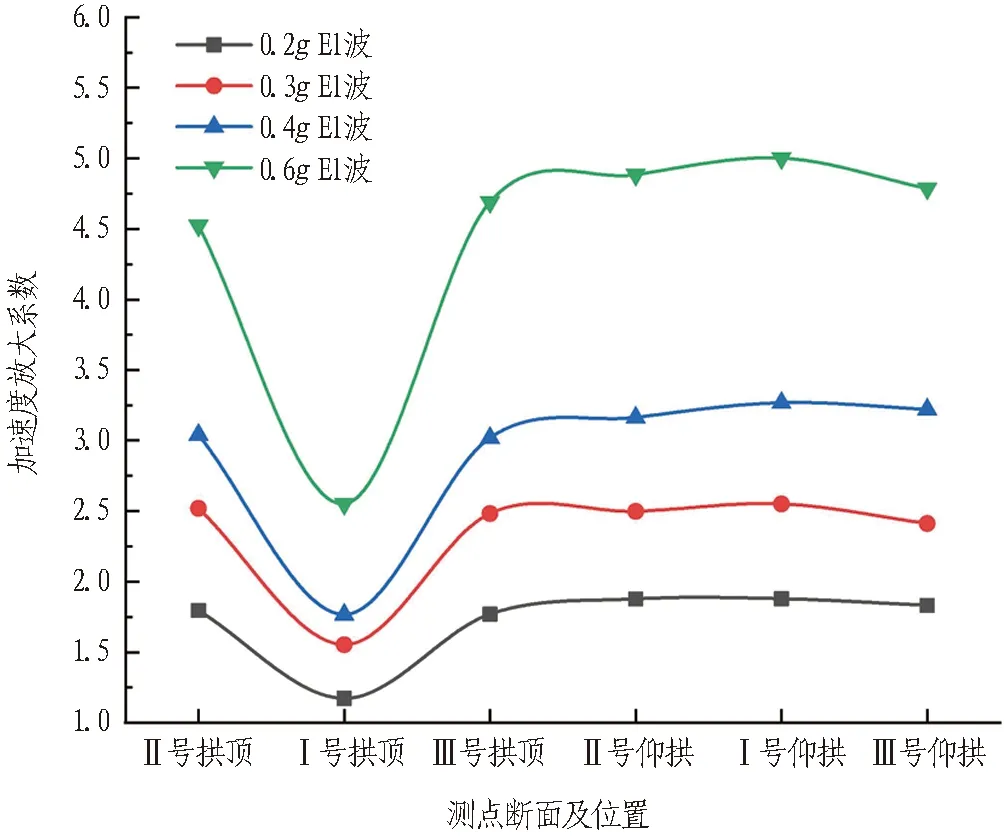
图8 X向上跨隧道加速度峰值放大系数
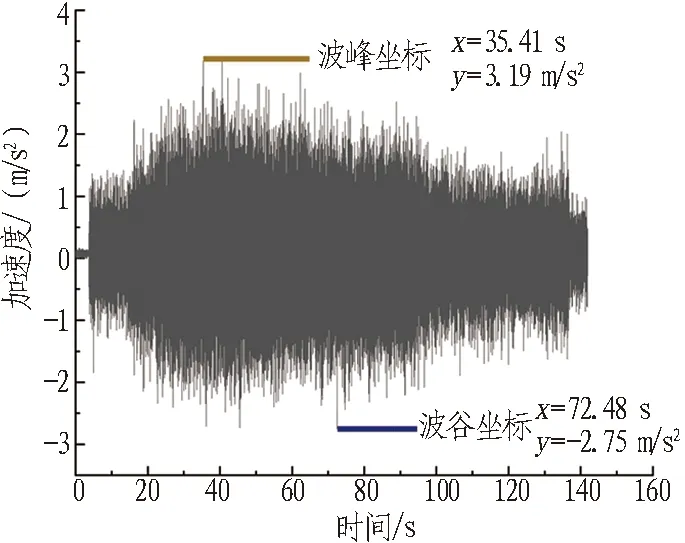
(a) 0.05g正弦扫频
2.1.2 下穿隧道加速度峰值分布
对下穿隧道拱顶及仰拱轴向加速度峰值进行同样分析,以上下横轴为拱顶及仰拱的不同断面位置,左右纵轴为加速度峰值,绘制其加速度峰值分布,如图10所示。
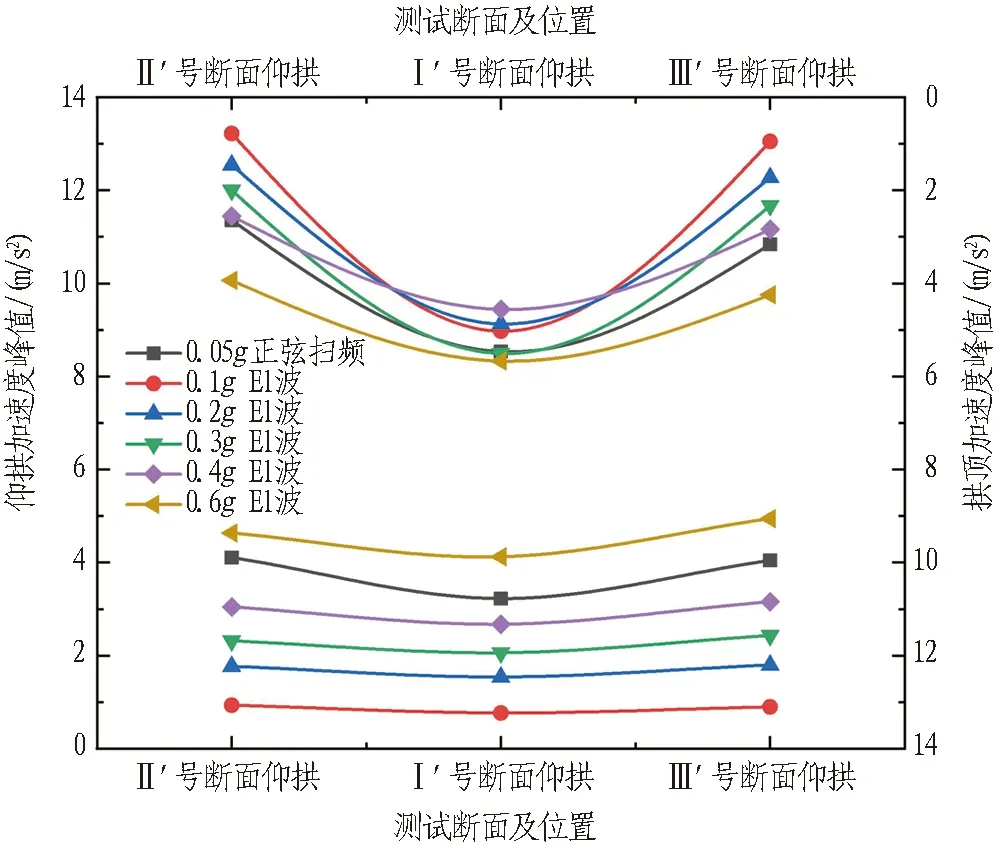
图10 X向下穿隧道加速度峰值分布
由图10可知: 下穿隧道轴向加速度峰值分布也呈现出明显的规律性: 随着加载工况的增大,各测试断面位置处的加速度峰值随之增大;对于下穿隧道拱顶,交叉段中心Ⅰ′号断面处加速度峰值最大,其次为影响区段Ⅲ′号断面,Ⅱ′号断面加速度峰值最小,且同一工况下不同断面处的分布也近似呈“抛物线”分布; 对于下穿隧道仰拱,交叉段中心Ⅰ′号断面处加速度峰值最小,影响区段两侧Ⅱ′、Ⅲ′号断面处加速度峰值基本相等,且同一工况下不同断面处加速度峰值变化不大; 这也说明在地震过程中受到围岩等的挤压, 隧道拱顶外侧的振动往往更剧烈,应重点关注拱顶外侧的抗震设计。
为了更加明显地表达不同工况下隧道拱顶及仰拱的变化趋势,以0.1gEl波工况为基准,分析其他工况下的加速度放大系数,其中0.1gEl波工况下Ⅰ′、Ⅱ′、Ⅲ′号断面拱顶(仰拱)的加速度峰值分别为3.94、0.78、0.94 m/s2(0.77、0.93、0.90 m/s2),结果如图11所示。由图可以看出,交叉段中心Ⅰ′号断面拱顶处加速度峰值变化基本不大,各工况下其放大系数在1.0附近徘徊,这是由于结构模型在试验过程中逐渐产生损伤,刚度降低,变形能力增强,耗能能力增强,使得其加速度放大系数相对较低。
同时也分析了交叉段中心Ⅰ′号断面拱顶处(XA2测点)在不同加载工况下的加速度时程曲线,如图12所示。通过时程曲线也可以看出,随着加载El波幅值的增大,下穿隧道拱顶处加速度响应变化较为平稳。在加载0.1g~0.6gEl波时,其峰值加速度分别为4.04、3.94、4.02、4.12、4.20 m/s2且加速度峰值基本出现在加载后20~40 s。
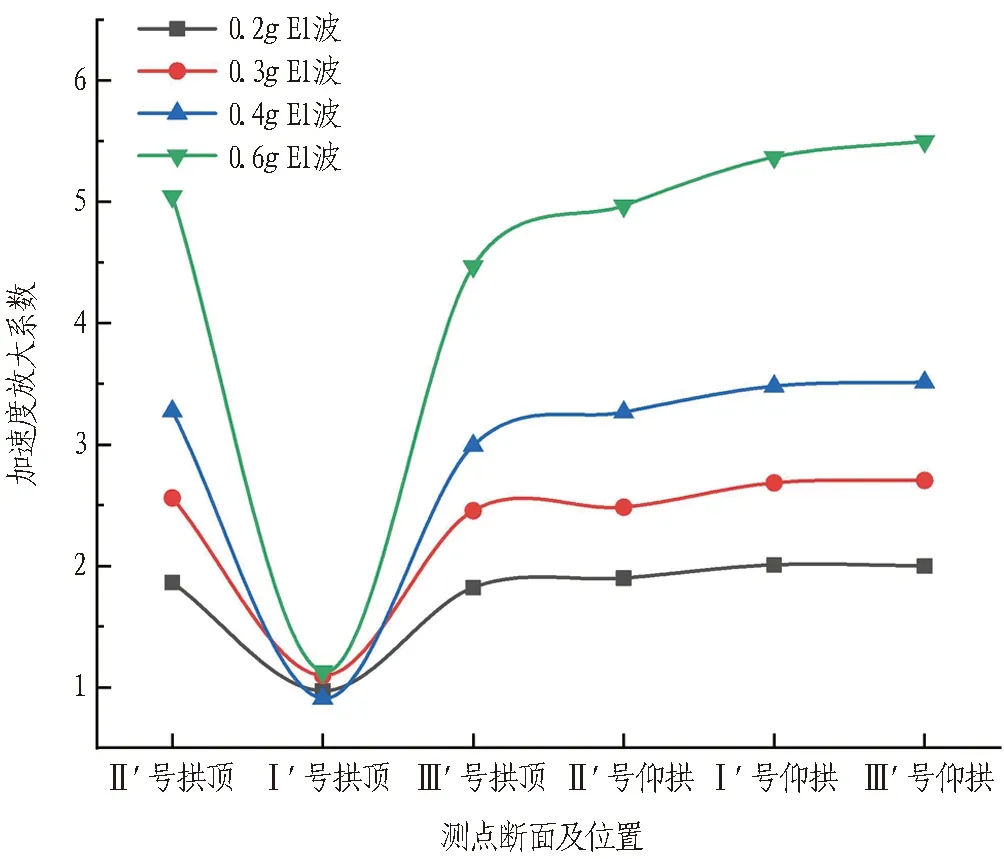
图11 X向下穿隧道加速度峰值放大系数
2.1.3 坡体内部加速度峰值分布
为了对比坡体内部有无隧道部位加速度响应的异同,沿隧道交叉段竖向中线位置进行分析,即坡体内部竖向中心线PA1~PA4测点。其加速度峰值分布如图13所示。
由图13可知,坡体内部各测点(除两隧道交叉中心段测点PA3外)加速度峰值沿高程存在放大效应; 且在同一工况下,交叉中心段测点PA3的加速度峰值均大于坡体其他部位; 同时可以看出在输入El波峰值为0.1g~0.3g时,其放大效应不明显,而在0.3g以后,其沿高程放大效应较为明显; 以PA4测点为基准点,在工况0.4g及0.6g时,可以得出PA2及PA1测点加速度放大系数分别为1.05、1.16及1.07、1.23,即加速度放大系数在坡底处较小,而在坡顶处较大。
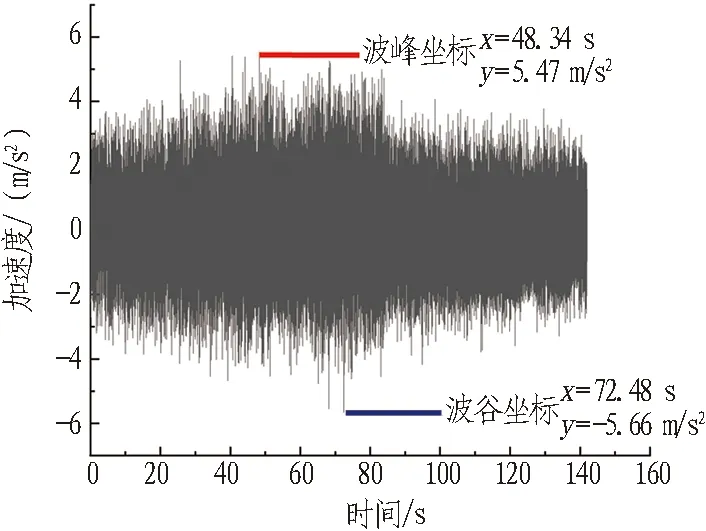
(a) 0.05g正弦扫频
2.2 XZ耦合双向加载时加速度峰值分析
2.2.1 上跨隧道加速度峰值分布
在加载XZ耦合双向El-Centro波时,上跨隧道轴向加速度峰值分布如图14所示。
XZ双向耦合加载时上跨隧道轴向加速度峰值分布及变化与X向加载时的规律性基本相似: 上跨隧道拱顶处加速度峰值近似呈“抛物线”分布; 仰拱处加速度峰值在同一工况下由Ⅱ、Ⅰ、Ⅲ号断面逐渐增加,近似呈“斜直线”分布。另外可以看出,交叉段中心Ⅰ号断面仰拱处加速度峰值明显小于拱顶处,且在各工况下同一断面测点处其加速度峰值都大于X向加载。
同理,以0.1gEl波工况为基准,分析其他工况下的加速度放大系数,其中0.1gEl波工况下Ⅰ、Ⅱ、Ⅲ号断面拱顶(仰拱)的加速度峰值分别为3.81、0.63、0.86 m/s2(1.05、0.92、1.92 m/s2),结果如图15所示。
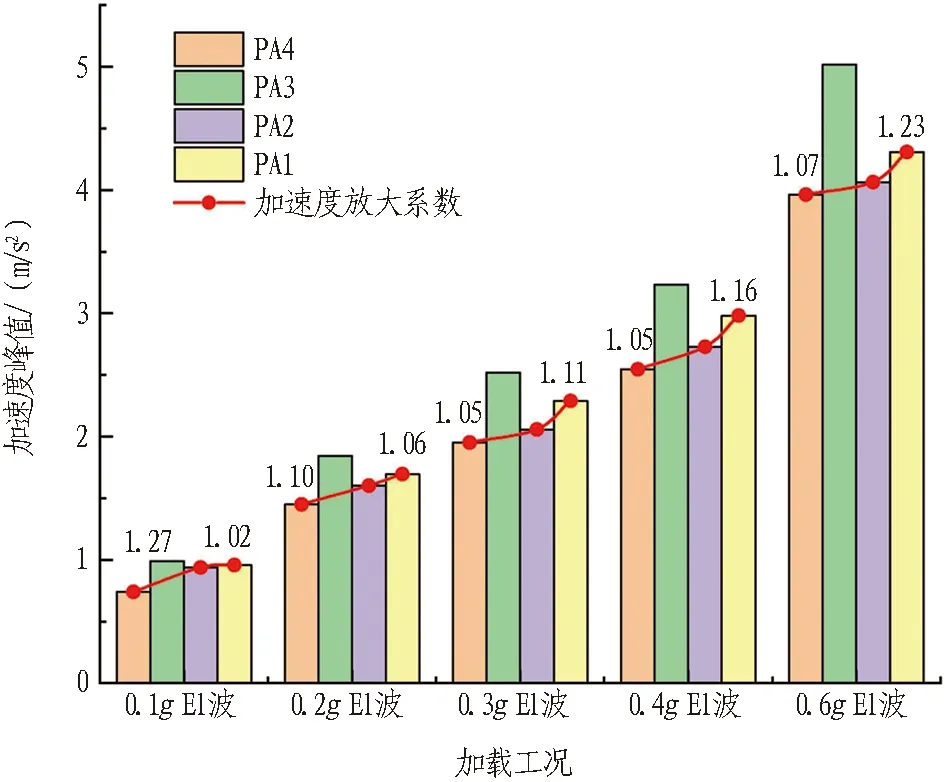
图13 X向坡体内部加速度峰值及其放大系数分布
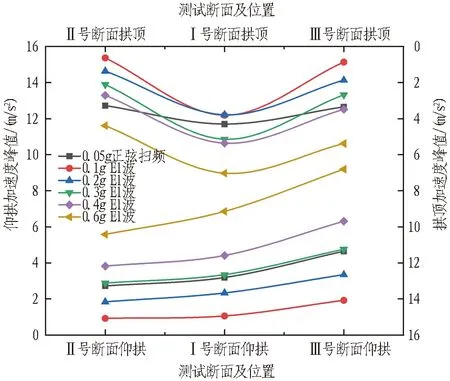
图14 XZ向上跨隧道轴向加速度峰值分布
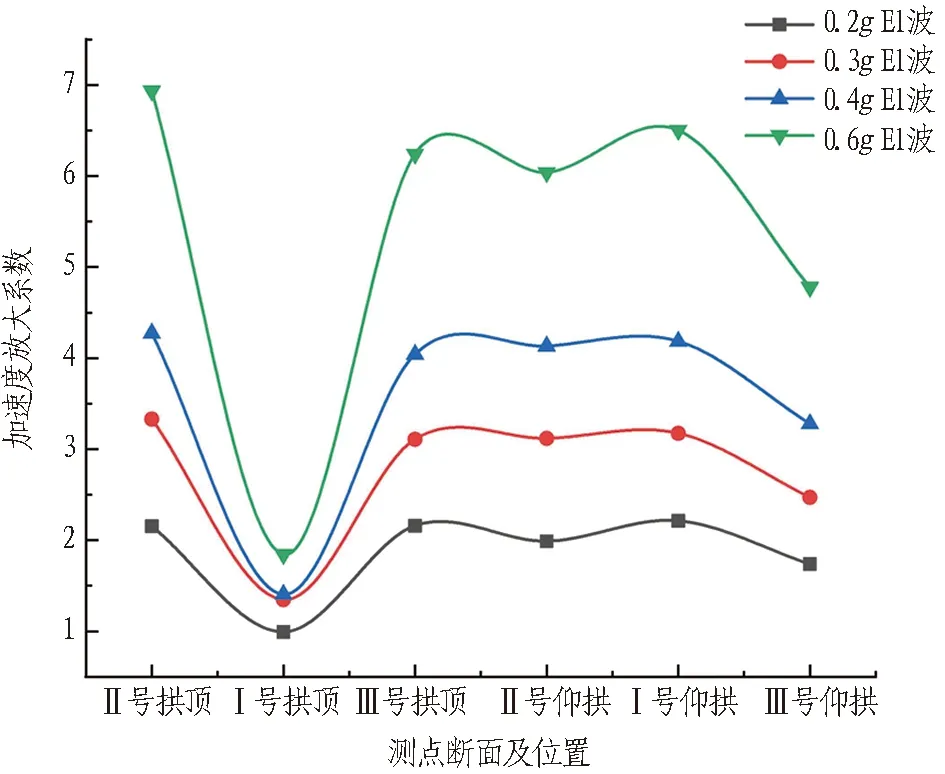
图15 XZ向上跨隧道加速度峰值放大系数
由图15可以看出,各工况下Ⅰ号断面拱顶处的加速度放大系数最小,而其次隧道仰拱处,从地震波传递的角度来考虑,由于结构地震作用是由模型箱底部传递到隧道仰拱—拱顶, 这也是导致这一现象产生的原因之一。且在0.2g~0.4g加速度放大效应增幅较小,加速度放大系数最大为3.33; 而在0.4g以后其加速度放大系数出现了明显的突增,最大达到6.93。
为了能够更加详细地表现El波在XZ耦合双向加载时加速度的动力响应,对交叉段中心Ⅰ号断面仰拱处(SA5测点)在不同加载工况下的加速度峰值进行了分析,如表3所示。由表3可以看出,随着加载El波幅值的增大,上跨隧道仰拱处加速度响应也越强烈。在加载0.1g~0.6gEl波时,其峰值加速度分别为1.05、2.33、3.29、4.39、6.85 m/s2,且峰值加速度基本出现在加载后20~50 s。

表3 XZ向上跨隧道仰拱处(SA5测点)加速度峰值
2.2.2 下穿隧道加速度峰值分布
在加载XZ耦合双向El-Centro波时,下穿隧道具体加速度峰值分布如图16所示。
由图16可知,在XZ双向加载时,下穿隧道轴向加速度峰值分布与X单向加载时呈现出相同的规律: 对于下穿隧道拱顶,交叉段中心Ⅰ′号断面处加速度峰值最大,其次为影响区段Ⅱ′号、Ⅲ′号断面,且同一工况下不同断面处的分布也近似呈“抛物线”分布; 而对于下穿隧道仰拱,交叉段中心Ⅰ′号断面处加速度峰值最小,影响区段两侧Ⅱ′、Ⅲ′号断面处加速度峰值基本相等,且同一工况下不同断面处加速度峰值变化不大; 在0.1g~0.4g工况下,各断面拱顶处的加速度峰值均大于仰拱,而在0.4g~0.6g工况下,Ⅱ′及Ⅲ′断面拱顶处的加速度峰值小于仰拱。
以0.1gEl波工况为基准,分析其他工况下的加速度放大系数,其中0.1gEl波工况下Ⅰ′、Ⅱ′、Ⅲ′号断面拱顶(仰拱)的加速度峰值分别为5.94、0.84、1.18 m/s2(0.96、1.04、0.97 m/s2),结果如图17所示。

图16 XZ向下穿隧道轴向加速度峰值分布
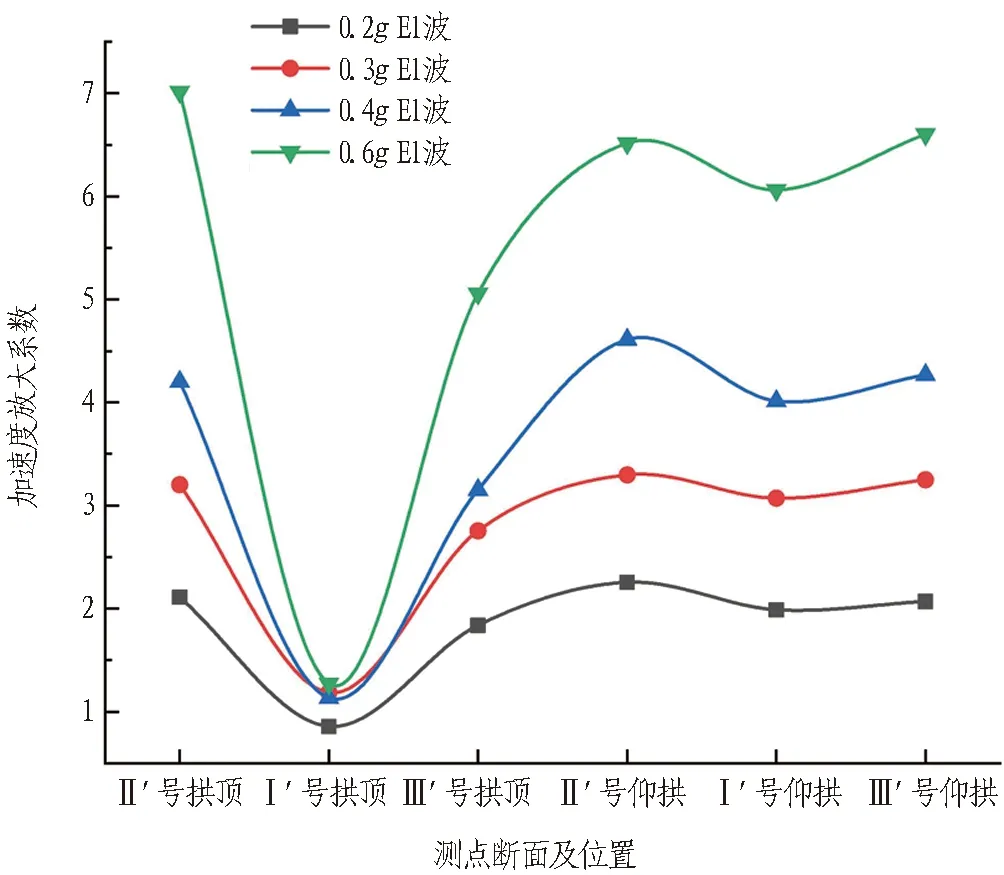
图17 XZ向下穿隧道加速度峰值放大系数
由图17可以看出,各工况下各断面测点呈现出明显的规律性,其加速度放大系数由大至小依次为: Ⅱ′号拱顶>Ⅲ′号仰拱>Ⅱ′号仰拱>Ⅰ′号仰拱>Ⅲ′号拱顶>Ⅰ′号拱顶; 且在0.2g~0.4g加速度放大效应增幅较小,加速度放大系数最大仅为3.30,而在0.4g以后其加速度放大系数出现了明显的突增,最大达到了7.02。产生这一现象的原因是: 地震响应的增大导致结构刚度减小,致使其对隧道的作用有所增大,从而导致峰值加速度响应突变。
为了能够更加详细地表现El波在XZ耦合双向加载时加速度的动力响应,对交叉段中心Ⅰ′号断面拱顶处(XA2测点)在不同加载工况下的加速度峰值进行了分析,如表4所示。由表4可以看出,随着加载El波幅值的增大,下穿隧道拱顶处加速度响应变化不大; 在加载0.1g~0.6gEl波时,其峰值加速度分别为5.90、5.94、5.86、5.97、6.00 m/s2,且峰值加速度基本出现在加载后30~40 s。
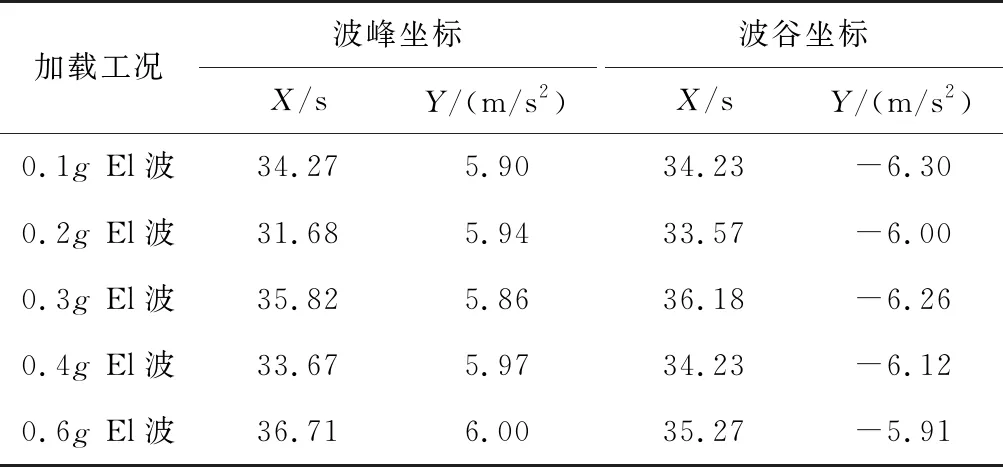
表4 XZ向下穿隧道拱顶处(XA2测点)加速度峰值
2.2.3 坡体内部加速度峰值分布
为了对比坡体内部有无隧道部位加速度响应的异同,对隧道交叉段竖向中线位置进行分析,即坡体内部竖向中心线PA1~PA4测点。其加速度峰值分布如图18所示。
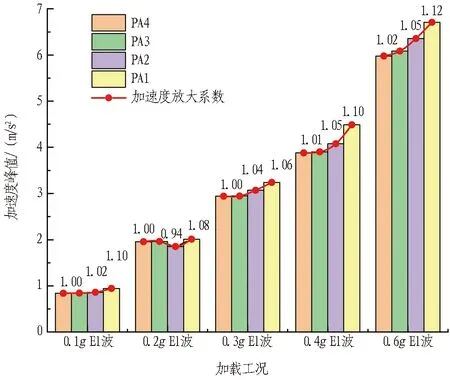
图18 XZ向坡体内部加速度峰值及其放大系数分布
由图18可知,坡体内部各测点(除在工况0.2gEl波外)加速度峰值沿高程存在放大效应; 在输入El波峰值较小时,其放大效应不明显,而在工况0.4g~0.6gEl波时,其放大效应较为明显; 以PA4测点为基准点,在工况0.4g及0.6g时,可以得出PA3、PA2、PA1测点的加速度放大系数分别为1.01、1.05、1.10及1.02、1.05、1.12倍。加速度放大系数在埋深较浅处较大,与高峰等[24]在研究不同埋深单一隧道的地震响应时,所得出加速度放大系数随着埋深的增大逐渐减小的理论相吻合。同时也可以看出,坡体内部在XZ向加载时各工况下加速度响应均大于X单向加载时。
2.3 不同的加载方式下加速度响应的异同
为了探究不同加载方式下隧道主要位置(拱顶及仰拱)的响应特征,选取断面Ⅰ及Ⅰ′的拱顶、仰拱及交叉段的典型测点SA2、SA5、PA3、XA2、XA5对由于加载方向不同而带来的差异性进行分析。具体如图19所示。
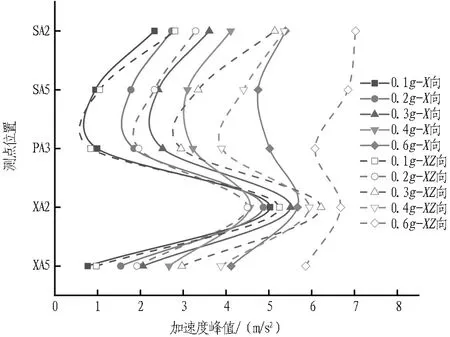
图19 不同加载方式下隧道各位置的加速度响应
由图19可以看出,在加载X单向及XZ双向El波时,立体交叉隧道的动力响应表现出的规律基本一致: 在隧道的拱顶处其加速度响应较大,且下穿隧道拱顶由于叠加效应,其地震响应最大; 而仰拱处的加速度响应相较于拱顶较小,且下穿隧道仰拱由于围岩对地震波的吸收作用较强,其加速度峰值最小。由此表明,立体交叉隧道拱顶地震响应较为强烈,易成为立体交叉隧道抗震的薄弱环节。
为了更加清晰地表达加载X单向及XZ向时测点加速度响应的异同,提取出0.1g~0.6g工况下各测点的加速度峰值,并定义加速度比率
(1)
式中:axz为xz方向加载;ax为x方向加载。
即在同一工况下加载XZ双向与X单向地震波时测点加速度峰值的比值,计算出各工况下Δa的值如表5所示。
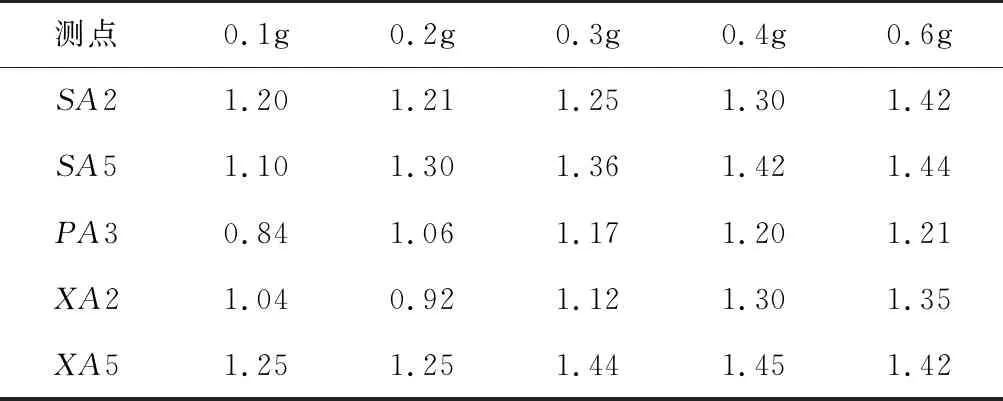
表5 同一工况下隧道各位置的加速度比率
由表5可知,在加载XZ双向地震波时,其同一测点在不同工况下的动力响应相较于只加载X单向时也显著增加; 在0.1g~0.3g时这种增长现象较为缓慢,而在0.4g~0.6g时变化幅度较大。以SA5为例,在加载0.1g~0.6g X向及XZ向地震波时其加速度峰值分别为0.95、1.78、2.42、3.10、4.75m/s2及1.05、2.33、3.29、4.39、6.85m/s2,对应加速度比率Δa分别为1.10、1.30、1.35、1.42、1.44,表明XZ双向耦合高地震烈度El波对于立体交叉隧道结构更为敏感。
此外,由表5还可以看出立体交叉隧道仰拱处的加速度比率Δa基本都大于拱顶处,说明地震波加载方向的改变对仰拱处地震响应产生更大的影响,而坡体内部加速度响应受到地震波加载方向的影响相对较小。
3 结论及建议
3.1 结论
通过立体交叉隧道振动台试验,分别研究了加载X单向及XZ双向El波时,上跨和下穿隧道及交叉区段坡体内部加速度峰值的分布规律,得到以下结论:
1)上跨隧道拱顶加速度峰值在交叉段中心断面处最大,影响区段两侧断面加速度峰值基本相等,呈现出“抛物线”分布,表明拱顶易成为立体交叉隧道抗震的薄弱环节; 由于下穿隧道的存在限制了上跨隧道仰拱处的变形,对上跨隧道仰拱交叉段中心断面处地震响应有明显的削弱作用。
2)对于立体交叉隧道工程而言,拱顶破坏模式表现为交叉区段中心断面—影响区段两侧断面的传递演化形式,而仰拱的地震响应正好与之相反,即影响区段两侧断面>交叉区段中心断面。
3)由于立体交叉隧道在地震波作用下两隧道之间往往会产生复杂的反射及折射现象,坡体内部交叉中心段的加速度响应存在叠加效应,表现最为强烈。同时坡体内部各测点加速度峰值沿高程存在着放大效应,且加速度放大系数随着测点埋深的增大而逐渐减小。
4)在输入XZ双向El波时,其同一测点在不同工况下的动力响应相较于只加载X单向时较为显著,且在0.1g~0.3g时这种增长现象较为缓慢,而在0.4g~0.6g时变化幅度较大。此外,地震波加载方向的改变对仰拱处地震响应会产生更大的影响。
3.2 建议
目前仅对斜交型立体交叉隧道的地震动力响应进行了初步探索,后续针对正交型立体交叉隧道的研究及2种不同交叉形式差异的动力响应还有待更进一步研究。
