考虑冻结管影响范围的多管冻结温度场研究
2021-02-24欧阳奥辉赵汝亮
向 亮, 叶 飞, 梁 兴, 欧阳奥辉, 赵汝亮, 3
(1. 中铁第一勘察设计院集团有限公司, 陕西 西安 710043; 2. 长安大学公路学院, 陕西 西安 710064;3. 天津市市政工程设计研究总院, 天津 300450)
0 引言
人工冻结法加固地层效果良好、地表沉降易控制,因此在地下空间领域应用越来越广泛,对其施工过程中产生的温度场的研究也如火如荼[1-3]。
目前,研究人工冻结温度场的手段很多,其中包括数值模拟、模型试验、理论分析以及现场实测调研等[4-6]。1954年,特鲁巴克[7]首先提出了单管冻结温度场的计算公式; 巴霍尔金基于理想冻结管相互影响模型和水力学相关概念得到单排管和双排管冻结壁交圈后的温度场分布特点[1]。文献[8-9]提出单排管冻土帷幕温度场的计算公式,并在实际工程中得到广泛实践。汪仁和等[10]基于平面单管传热模型,提出了双孔和多孔冻结的温度场叠加公式。李方政[11]通过指数积分函数,假设单管冻结为一维轴对称问题,得出人工冻土瞬态温度场的解析解,并分析了冻结交圈时间和冻结发展规律。胡向东等[12]对特鲁巴克解和巴霍尔金解进行修正,提出土体冻结温度不为零时的冻结温度场计算模型,并采用势函数叠加原理提出单排、双排和3排冻结管的稳态温度场求解方法。刘健鹏等[13]针对南京地铁盾构隧道端头加固冻结,推导了多排管冻结壁的平均温度计算公式。肖朝昀等[14]从冻结厚度和深度上分析了多排管局部冻结的温度发展特征,并计算出了积极冻结期结束时的冻土壁厚度。杨平等[15]以软土隧道联络通道冻结为背景,进行全程温度实测,探索施工中温度场的发展规律。对于平面斜交联络通道,马俊等[16]通过温度与位移实测,分析了冻结温度场发展规律及地表位移变化规律。
实际工程中,冻结管的影响范围并不是无限的,冻结管的布置间距往往会大于积极冻结期内单管冻结锋面半径。然而,目前,学者们考虑冻结管叠加影响范围的较少。为提高冻结管温度场计算的准确性,本文将冻结管影响范围假定为双管冻结范围,并推导双管冻结条件下叠加场范围的温度表达式,然后进行周期扩展,得到多管冻结条件下叠加温度场的分布形式。同时,依托兰州轨道1号线联络通道,通过数值模拟对推导的表达式进行验证,最后按照工程实际布管进行计算,并对设计方案进行验证。
1 多管冻结条件下叠加温度场计算
1.1 单管冻结条件下的稳态温度场计算
多管冻结温度场可认为是考虑相互作用影响下的多个单管冻结温度场的叠加,因此研究单管冻结是基础。由于冻结管的半径远小于其长度,可将其作为平面内冷源的热传导问题进行研究。在计算分析之前先做如下假设:
1)冻结管的温度辐射仅发生在垂直于轴线方向;
2)待冻结土体均质连续,且冻结前初始温度相同;
3)无穷远处的温度为地层初始温度;
4)假定土体冻结温度为0 ℃;
5)不计相变发生的时间,不考虑水分迁移,当某点达到冻结温度时,即可认为该位置土体已经冻结。
单管冻结计算模型如图1所示。

Ⅰ为冻结区; Ⅱ为未冻区; r0为冻结管半径; R为冻结锋面半径。
稳态温度场是一种理想中的温度分布模型,其温度分布以固定形式表示,见式(1)。
(1)
式中: 温度T为距冻结管中心的距离r的函数;r为任意点距离冻结管中心的距离;
由假设条件可得下列边界条件:
T(R)=Td; (2)
T(r0)=Tp。 (3)
式(2)—(3)中:Td为冻结温度;Tp为冻结管中心温度;r0为冻结管半径, m;R为冻结锋面半径(即冻结壁厚度), m。
取冻结温度Td为0 ℃时,代入边界条件式(2)和式(3)可得特鲁巴克单管冻结公式
(4)
1.2 双管冻结条件下的叠加温度场计算
由式(4)可知,在某一时刻单管冻结形成的温度与距离呈对数函数单调变化。冻结管对未冻区的影响较小,且实际冻结管布置间距大于单管冻结锋面半径,因此可假设相邻双管冻结时仅2冻结管之间的区域受叠加影响,即图2中x轴[O1,O2]区间,且以下计算坐标原点为O1。

图2 双管冻结计算模型
如图2所示,2个冻结管的冻结锋面刚好相切时,2个冷源周围的温度场是关于直线M1M2对称的,因此可假设2个冷源同时开始冻结,研究范围进而可缩小至[0,l/2]区间。
胡向东等[12]提出了温度势函数的概念,在单管冻结模型中,取半径为r的一个圆形界面,其表达形式为
(5)
式中:Q是半径为r的界面上任一点可通过的热量, kJ/(m·s);q是半径为r的界面上单位时间单位长度上的总热流量, kJ/(m·s);C0为积分常数。
依照上述假定条件,相邻双管冻结时仅2个冻结管之间的区域受叠加影响。2场叠加范围内任意点A(x,y)受相邻2个冻结管的热量QA(x,y)和QA′(x,y)的影响,受到的热量之和
Q(x,y)=QA(x,y)+QA′(x,y)=
(6)

由于2个温度的参数完全一致,A(x,y)点标量Q的表达式为
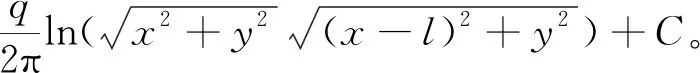
(7)
由此可得冻结锋面和冻结管外表面上的标量值Qd和Qp。
(8)
(9)
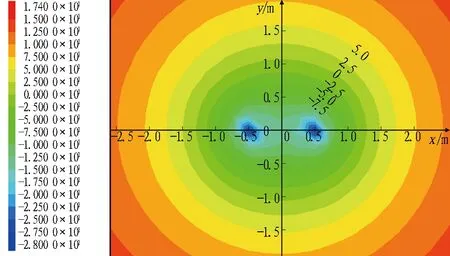
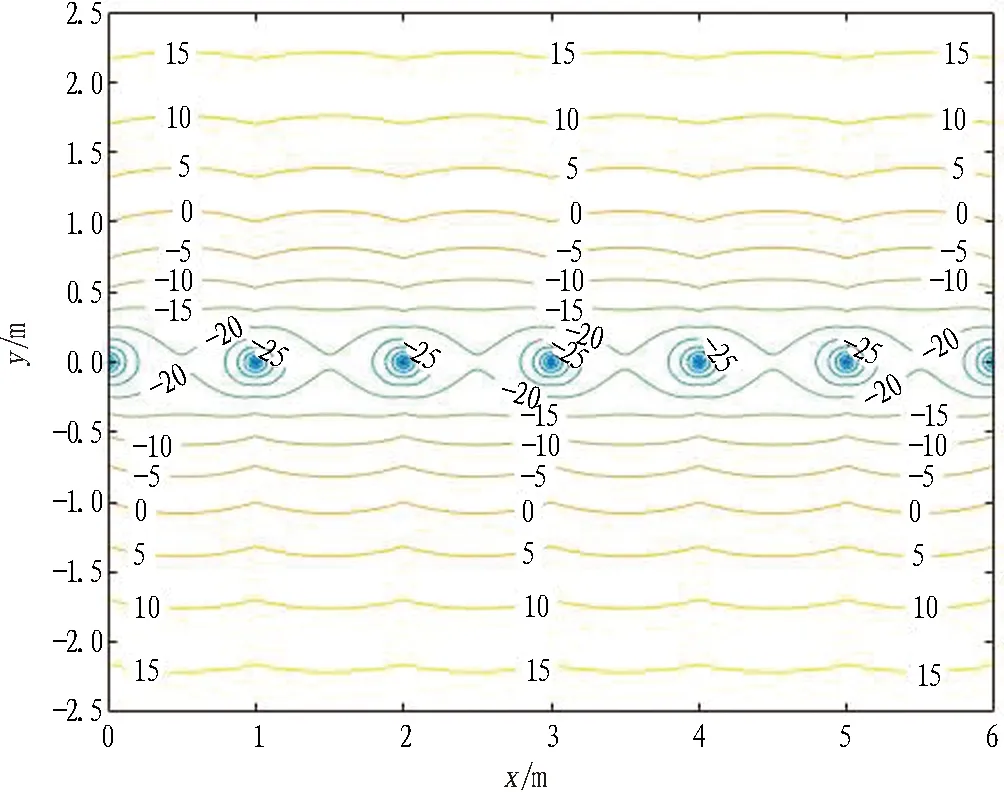
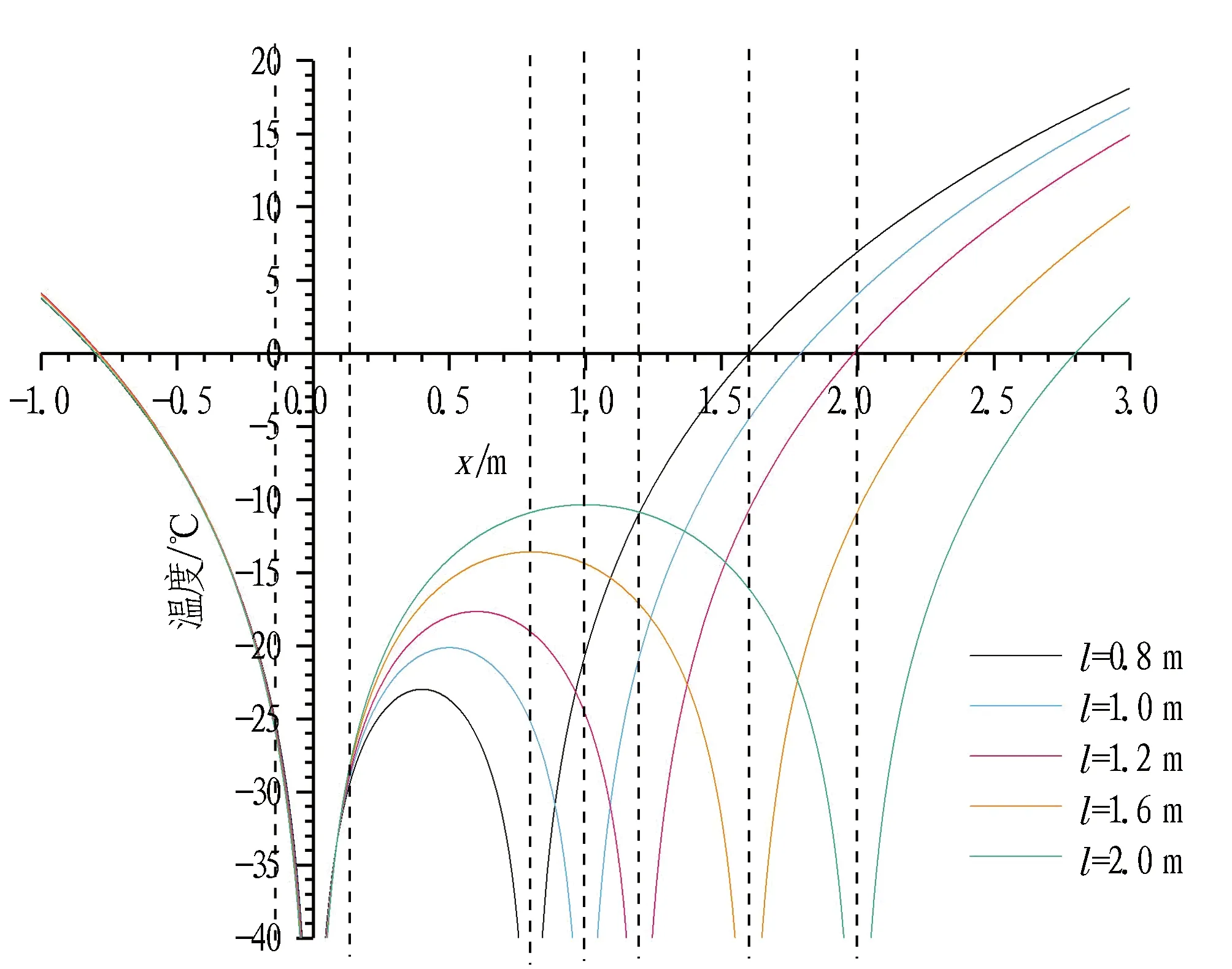
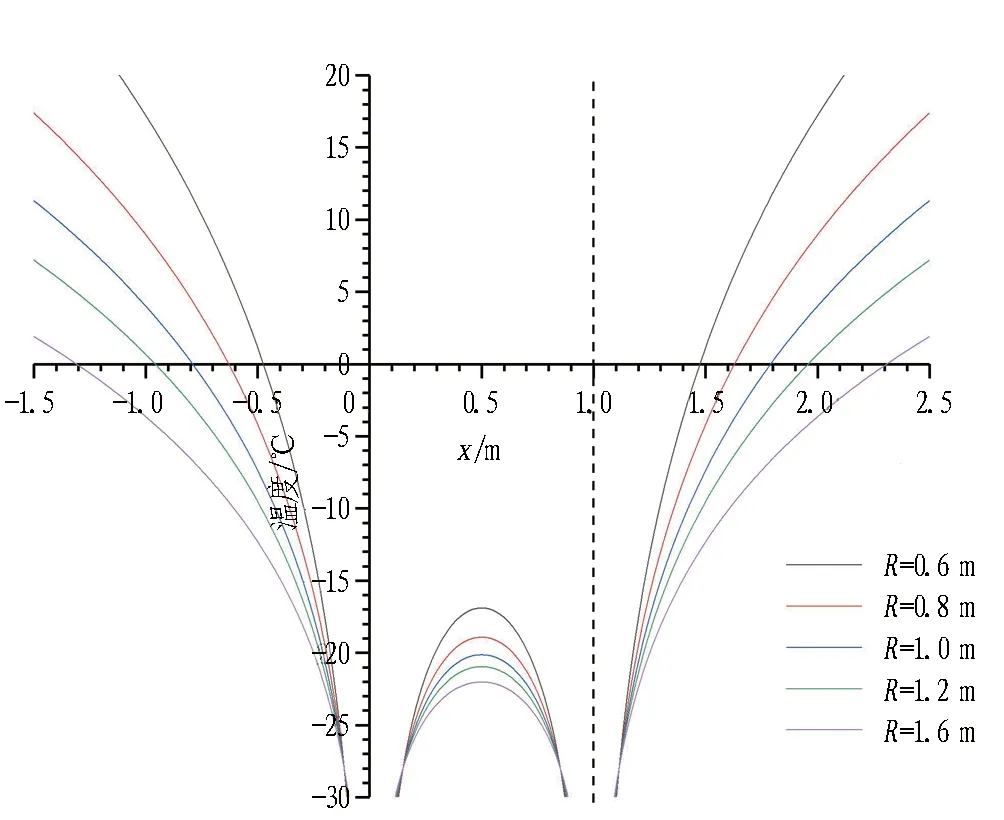
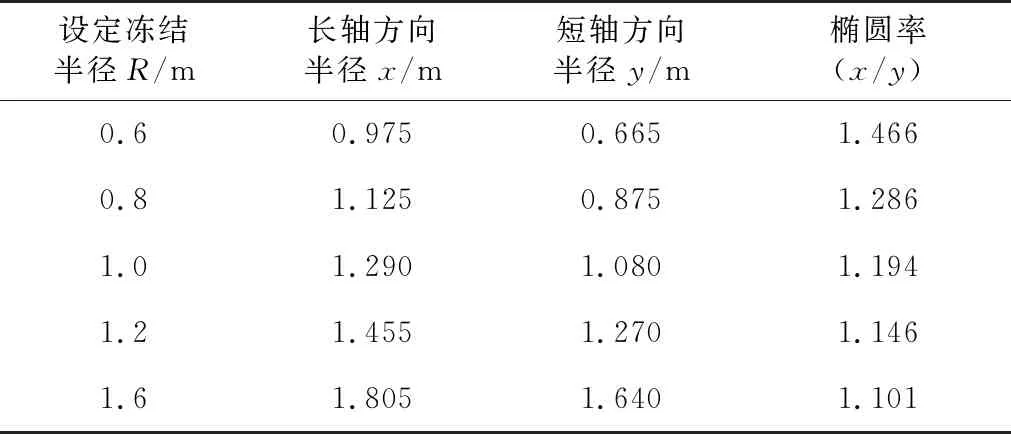
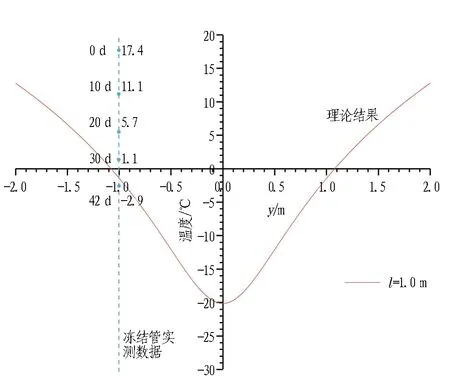
由于冻结管半径远小于冻结管间距,即r0< 由式(8)和式(9)联立可得 (10) 取冻结锋面为标量Q的零点,可得 (11) 将式(10)和式(11)代入式(7)可得到双场叠加区内Q的最终表达式: (0≤x≤l)。 (12) 取土体的冻结温度Td=0 ℃、Q=λT(λ为导热系数)可求得双管冻结条件下叠加场范围的温度表达式 (0≤x≤l)。 (13) 2.1.1 双管温度场分布 为验证本文提出的温度场计算模型的合理性,此处结合兰州地铁1号线联络通道所在的红砂岩地层进行计算,并通过FLAC 3D进行算例的模拟计算,对结果进行分析和验证。根据地勘报告和冻结设计方案,冻结计算参数取值见表1,红砂岩地层热物理参数见表2。 表1 冻结计算参数取值 表2 红砂岩地层热物理参数取值 根据设计要求,依托工程的冻结壁厚度需要在40 d达到单侧1 m的厚度。取冻结壁厚度R为1 m、冻结管间距l为1 m,在冻结管中心温度Tp取-28 ℃情况下,双管冻结稳态温度场分布如图3所示。 图3 双管冻结温度分布图(l=1 m,R=1 m)(单位: ℃) 通过FLAC3D建立50 m×50 m×10 m的平板模型,模型初始温度设置为-28 ℃,地层温度设置为17.4 ℃,建立2个冷源(圆柱),直径为0.127 m,长度为10 m,间距为1 m,模型参数按表1和表2选取。通过模拟计算可以发现,在红砂岩地层中,相同布置条件下,40 d时的双管冻结壁厚度R刚好达到1 m,此时的温度分布情况如图4所示。 由图3和图4知,理论公式与数值模拟基本吻合,温度变化规律保持一致。双管冻结温度场呈近椭圆形分布,并以两管连线的中垂线为对称轴。受相互作用最明显的是两冻结管之间的区域,两边外侧部分受相邻冻结管的影响作用较小,等温线依旧近似呈同心圆分布。 图4 双管冻结模拟计算结果(l=1 m,R=1 m)(单位: ℃) 2.1.2 单排多管温度场分布 根据假设,单排多管冻结条件下的温度场函数可以看作是式(13)的周期函数。将x=0与x=l之间的函数图像周期重复可得单排多管冻结情况下的温度场分布。相同间距不同冻结壁厚度下的冻结温度分布如图5和图6所示。 图5 多管冻结温度分布(l=1 m,R=1 m)(单位: ℃) 同双管数值模拟类似,在平板模型中心布置10个大小相同的冻结管,间距1 m,单侧冻结壁厚度为1.6 m,冻结温度场如图7所示。 由图6和图7可知,理论公式与数值模拟计算的结果基本吻合,温度变化规律保持一致。在单排多管冻结条件下,相邻两管之间的冻结锋面及等温线都呈波浪形分布,且相邻冻结管连线的中垂线上冻结壁厚度达到最大值,与巴霍尔金单排冻结模型的结果一致。保持冻结管间距l不变,增加冻结管竖向冻结壁厚度R,整体冻结壁厚度也将相应的增加,反映在实际工程中,即冻结管布置完毕后,可通过调整冷媒温度来间接控制冻结壁厚度。 图6 多管冻结温度分布(l=1 m,R=1.6 m)(单位: ℃) 图7 多管冻结模拟计算结果(l=1 m,R=1.6 m)(单位: ℃) 与单管稳态温度场的计算类似,本文温度场计算模型推导也是将冻结管位置的竖向冻结壁厚度R作为已知量考虑的,一般根据工程经验取值。此处不妨先将其假设为单管冻结冻结壁厚度的k倍,结合算例探究冻结壁厚度R与冻结管布置间距l对温度场分布的影响。 2.2.1 冻结管间距对温度场分布的影响 为研究冻结管间距对双管稳态温度场的影响,保持其他参数不变,选取冻结管间距值l为0.8、1.0、1.2、1.6、2.0 m,计算得温度T在冻结管连线及其中垂线上的分布规律如图8和图9所示。为方便描述,以冻结管连线所在直线为x轴。 由x轴上的温度计算结果可知,冻结管两侧(之前假设的非温度叠加区域)的温度分布是对称的,且多条温度曲线在外侧几乎重合,这说明之前的假设是合理的,即相邻冻结管的影响区域有限,两边外侧温度仍按单管冻结形式分布,外侧冻结锋面半径约为0.81 m。在温度叠加区内,冻结管连线中点位置温度为最高值,同时也是中垂线上温度最低点,冻结管间距l越小,该点温度也越低。中垂线上冻结锋面位置不会随冻结管间距l改变,该方向上的冻结壁厚度的一半稳定在1.1 m左右,略大于设定的冻结壁厚度R。 图8 双管冻结时冻结管连线上的温度分布(R=1 m) 图9 双管冻结时冻结管连线中垂线上的温度分布(R=1 m) 2.2.2 竖向冻结壁厚度对温度场分布的影响 保持其他参数不变,当冻结管间距值l=1 m时,分别取竖向冻结壁厚度R为0.6、0.8、1.0、1.2、1.6 m,计算得温度T在冻结管连线及其中垂线上的分布规律如图10和图11所示。 随着设定冻结壁厚度R的增加,两边外侧冻结锋面半径和中垂线上的冻结锋面纵坐标都有了不同程度的增长,以外侧冻结区的发展最为明显,取比值如表3所示。由表3可知,随着R的增加,叠加温度场的形状逐渐向标准圆形靠近。类似于在实际工程中加设一补充冻结管,若其与附近冻结管的距离很近且冷源温度都很低时,可以将2个冻结管看作一个加强的冻结管。 图10 冻结管连线上温度分布规律 图11 冻结管连线中垂线上温度分布规律 表3 双管冻结时冻结管连线与其中垂线上冻结壁厚度(l=1 m) 2.2.3 关于k值的讨论 竖向冻结壁厚度R通常难以选取,需要根据测温孔实测温度反演确定,本节中假设双管冻结壁厚度为单管冻结壁厚度的k倍。 以数值模拟结果表示双管冻结瞬态温度场的分布,将模拟计算得出的叠加区冻结壁厚度最小值R与单管冻结壁厚度R′进行比较,冻结壁厚度随时间的发展规律如图12所示。经对比发现,两者的比值k为1.2~1.8,在一般积极冻结期30~60 d,k值基本稳定在1.6左右。 图12 双管冻结时冻结壁厚度变化规律 本文选取距单排冻结管相邻2冻结管中心线1 m处的测温管数据,与理论公式计算结果相对比,如图13所示。因本文讨论的是冻结稳态温度场分布,故以10 d为一间隔,给出该测温管处积极冻结期内的实测温度。经42 d积极冻结期后,该处温度降至-2.9 ℃,这证明单排管单侧冻结壁厚度已达1 m左右,与本文提出的双管冻结公式及数值模拟结果吻合,公式适用性较好。 图13 实测数据与理论计算结果对比 1)根据温度“势函数”的概念,考虑到相邻冻结管的叠加影响范围有限,对平面内双管温度场稳态模型的解析解进行了推导,并通过数值模拟验证了其合理性。 2)将双管冻结条件下的叠加温度场周期化,得到了单排等距多管温度场的分布规律,其计算结果与巴霍尔金解具有同样的规律。 3)在双管温度叠加区内,冻结管连线中点为中垂线温度的最低点,并随着冻结管间距l减小而减小,但中垂线上冻结壁厚度不随冻结管间距l改变。 4)随着冻结壁厚度R的增加,双管稳态温度场分布接近圆形,近似为一个加强单管稳态温度场。 5)结合兰州红砂岩地层进行了温度场模拟,得到了双管与单管2种条件下的冻结壁厚度比值k的取值为1.2~1.8; 在一般积极冻结期30~60 d,k值基本稳定在1.6左右,为兰州红砂岩这种特殊地层的冻结壁厚度设计提供了参考。 6)冻结管叠加范围下的冻结壁厚度R的取值仍需结合现场实测值进行研究。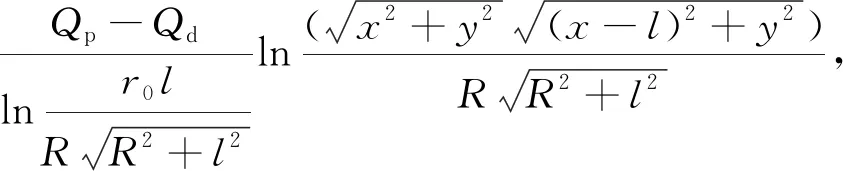
2 算例分析研究
2.1 红砂岩地层算例分析





2.2 参数分析



2.3 现场实测数据对比
3 结论与建议
