基于模糊比例积分微分算法的汽车半主动悬架振动分析
2021-02-24刘晓昂张佳琪
刘晓昂,张佳琪,王 爽
(1.河北工业大学机械工程学院,天津 300132;2.天津市新能源汽车动力传动与安全技术重点实验室,天津 300132; 3.大连民族大学机电工程学院,大连 116600)
目前大部分汽车上装备的是被动悬架,因其刚度以及阻尼等参数不能随路面工况实时变化,所以对振动的抑制能力有限。半主动悬架由于其出色的自适应能力,大大降低了汽车在行驶过程中的振动,因此成为当前汽车悬架研究的重点[1]。
文献[2]针对车辆座椅悬架采用了比例积分微分(proportion integration differentiation,PID)算法进行控制,座椅在垂向产生的振动大幅度减小,证明了PID算法应用在悬架系统的可行性。文献[3]分别采用T-S模糊算法和PID算法对悬架进行了半自动控制,两种算法均能产生不错的减振效果。文献[4]提出了一种自适应的模糊控制方法,并通过李雅普诺夫理论证明了所提出的控制策略能保证系统的稳定性,验证了所提控制策略的有效性。文献[5]针对模糊控制算法进行了优化,使其论域可变,增加了预测精度。文献[6]采用神经网络控制与粒子群优化方法相结合的方式,设计了一种新型的半主动悬架系统控制策略,使用该控制方法能够明显提升半主动悬架的性能。
由于PID算法参数不可变且采用单一控制方法不易达到汽车对于悬架系统振动抑制的要求。因此,针对汽车的半主动悬架系统建立1/4车辆简化模型和路面随机激励模型,引入模糊控制理论并与PID控制相结合,通过区分来自路面随机激励的不同而选取不同的PID参数,达到参数随时可调的目的。并将仿真结果与单纯由PID算法控制的悬架以及传统的被动悬架进行对比分析。探索更优秀的悬架控制策略,以提高汽车在面对路面冲击时的减振性能。
1 半主动悬架系统
1.1 半主动悬架系统动力学分析
半主动悬架由弹簧、阻尼和可控阻尼器构成[1]。路面激励通过车轮传递到半主动悬架系统,可控阻尼器产生作用力,减小激励所引起的振动,提高汽车行驶平顺性[7]。根据半主动悬架工作原理,建立的1/4汽车半主动悬架模型如图1所示。
对图1中的半主动悬架模型进行动力学分析,可以得到车身与轮胎的振动微分方程为
(1)
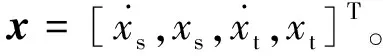
(2)
式(2)中:
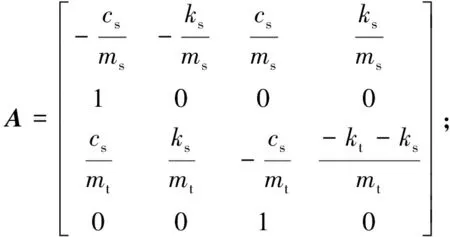
1.2 路面激励模型
在分析悬架系统振动性能时,来自路面随机激励的干扰需要着重对待。《机械振动 道路路面谱测量数据报告》(GB/T 7031—2005)将道路划分为8个等级,在进行实际测绘时,基本不能得到整体相同的两段路面轮廓曲线,这就会对研究结果的对比分析产生影响[9]。所以需要将已知的道路参数进行处理并计算出路面不平度。
路面系数Gq(n)需要经过转换才能作为1/4车辆简化模型系统的输入,其公式为
(3)
式(3)中:μ为车速;f0为下截止频率;n0为空间频率;Gq(n0)为空间频率下的道路系数;ω(t)为白噪声;q(t)为模拟的道路激励。
2 模糊PID控制器
PID算法是较早得到应用的控制算法,通过反馈的方式计算出调整值施加于受控对象,其数学表达式为
(4)
式(4)中:Kp、KI、KD为PID参数;e(t)为反馈变量;u(t)为输出的调整值。
在大部分需要控制的运动状态中采用PID算法可以达到出色的效果。然而,PID算法在面对比较复杂的运动系统时容易受到参数不可变的限制,在系统运行全程控制水平参差不齐,达不到理想的效果[10]。在实际应用中,手动的去调节控制器参数既费时又费力。因此针对PID参数不能随时改变的缺点引入了模糊控制策略,以实现PID参数随运动状态不断变换的目的,使车辆获得更好的平顺性。模糊PID控制原理如图2所示。
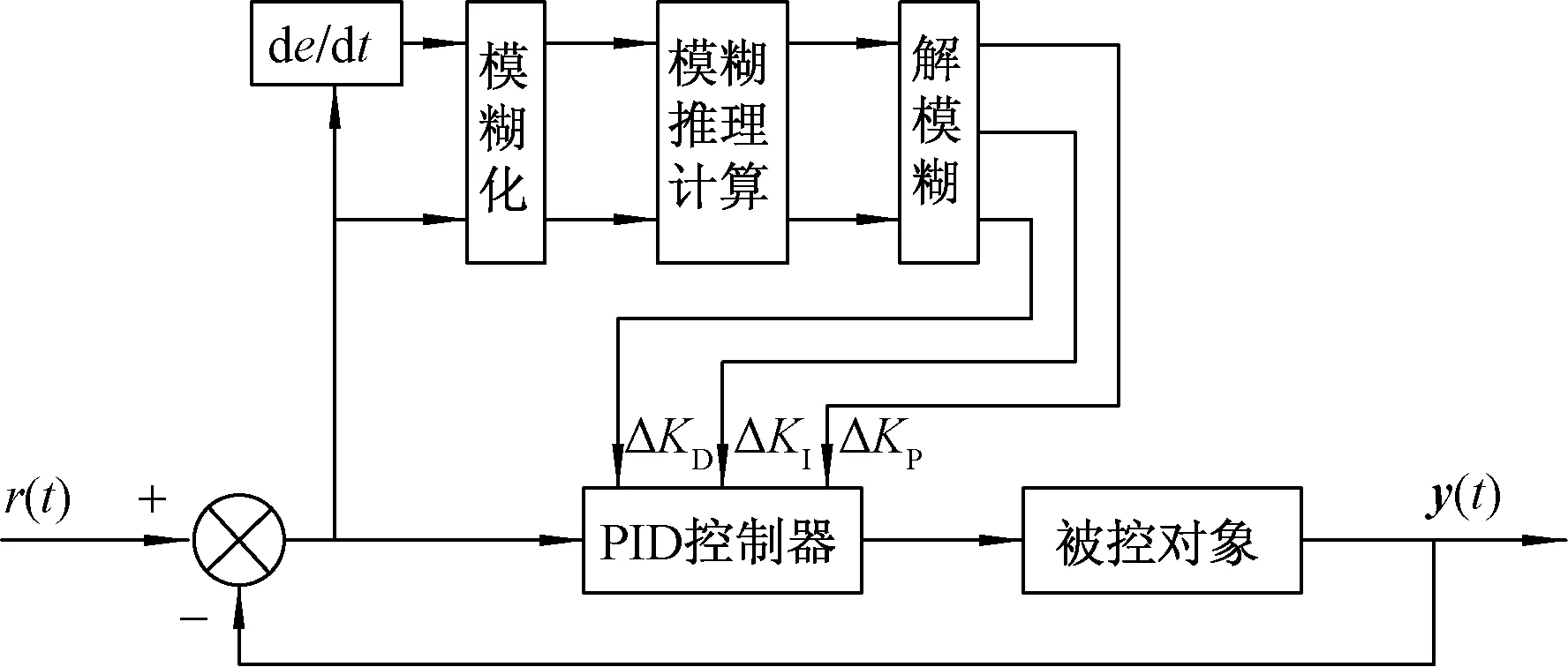
r(t)为模糊PID控制器的初始输入;ΔKP、ΔKI、ΔKD为PID参数调控量;y(t)为半主动悬架系统的输出
模糊控制器的输入选用车身与车轮垂向位移的差值(e)及变化速率(eα)两个变量,输出为ΔKP、ΔKI、ΔKD同时也是PID参数的调控量与差值(e)一起输入到PID控制器,经过式(4)计算最终输出为可控作用力(u)。
当模糊控制器工作时,由于输入e和eα的实际值变化范围过小与模糊控制器定义范围不符,会对输出参数的选取造成影响,达不到理想的控制效果,因此需要比例因子对e和eα进行放大。假设输入e和eα的实际范围为[-n,n]和[-m,m],其中n、m为任意实数,定义的模糊范围为[-3,3]。则比例因子Ke=3/n、Keα=3/m。
将输入和输出的模糊范围细分为7个等级[EA,EB,EC,D,FC,FB,FA],分别对应[-3,-2,-1,0,1,2,3]。参考文献[11]中给出的模糊规则对应关系,可以列出输入e、eα与输出ΔKP、ΔKI、ΔKD的变化规则。以输出ΔKP为例,ΔKP随e和eα的变化规则如表1所示,为便于查看将数据绘制成三维曲面,如图3所示。
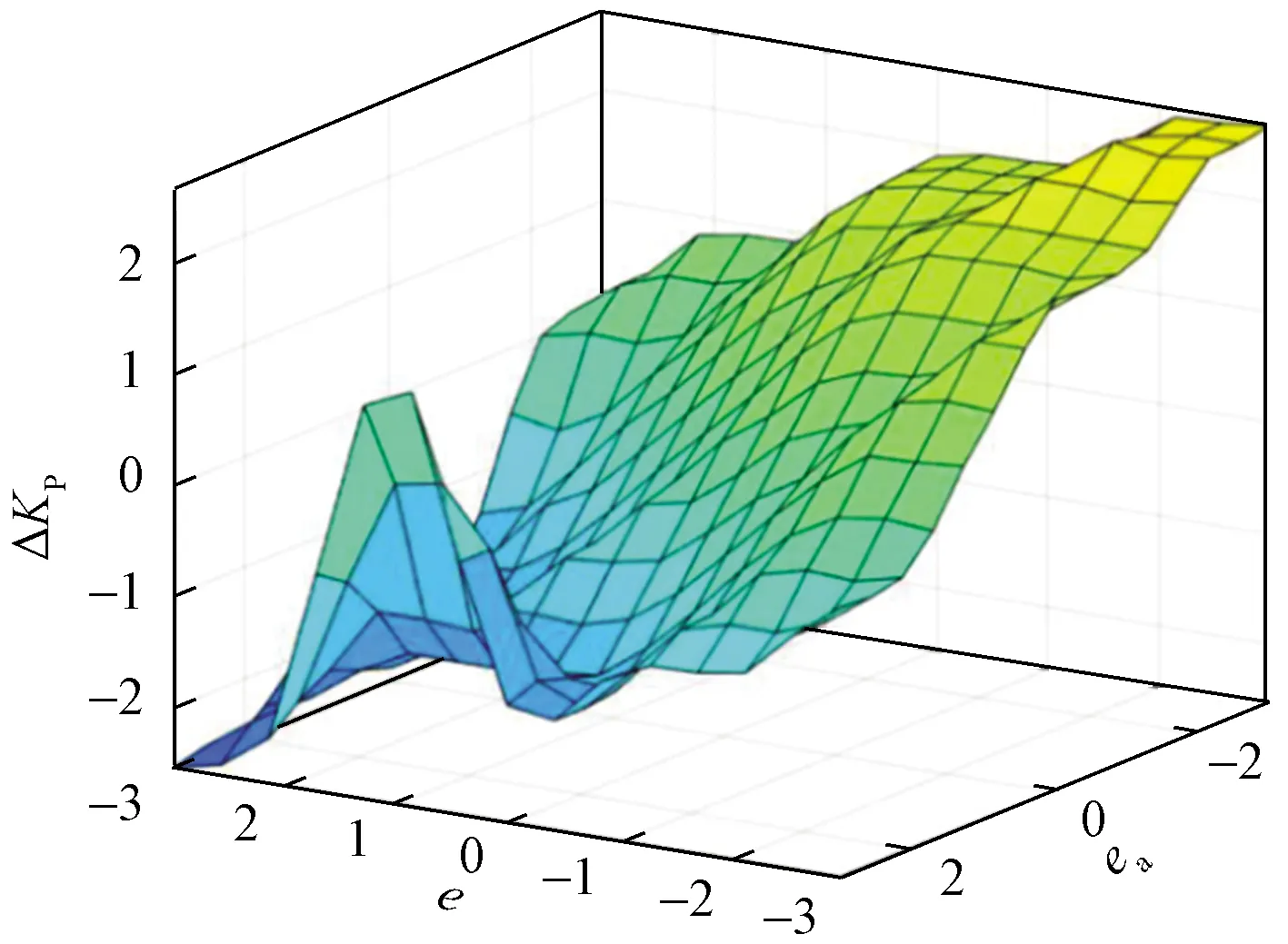
图3 ΔKP的关系曲面
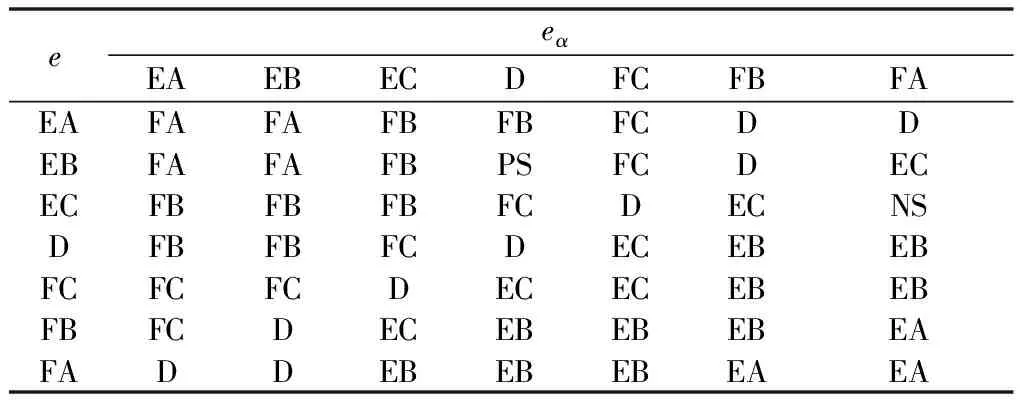
表1 ΔKP模糊控制规则
3 仿真模型的建立
悬架以及道路产生的垂向随机输入的时域模型主要通过仿真软件进行搭建。根据式(3)搭建的道路时域模型如图4所示。
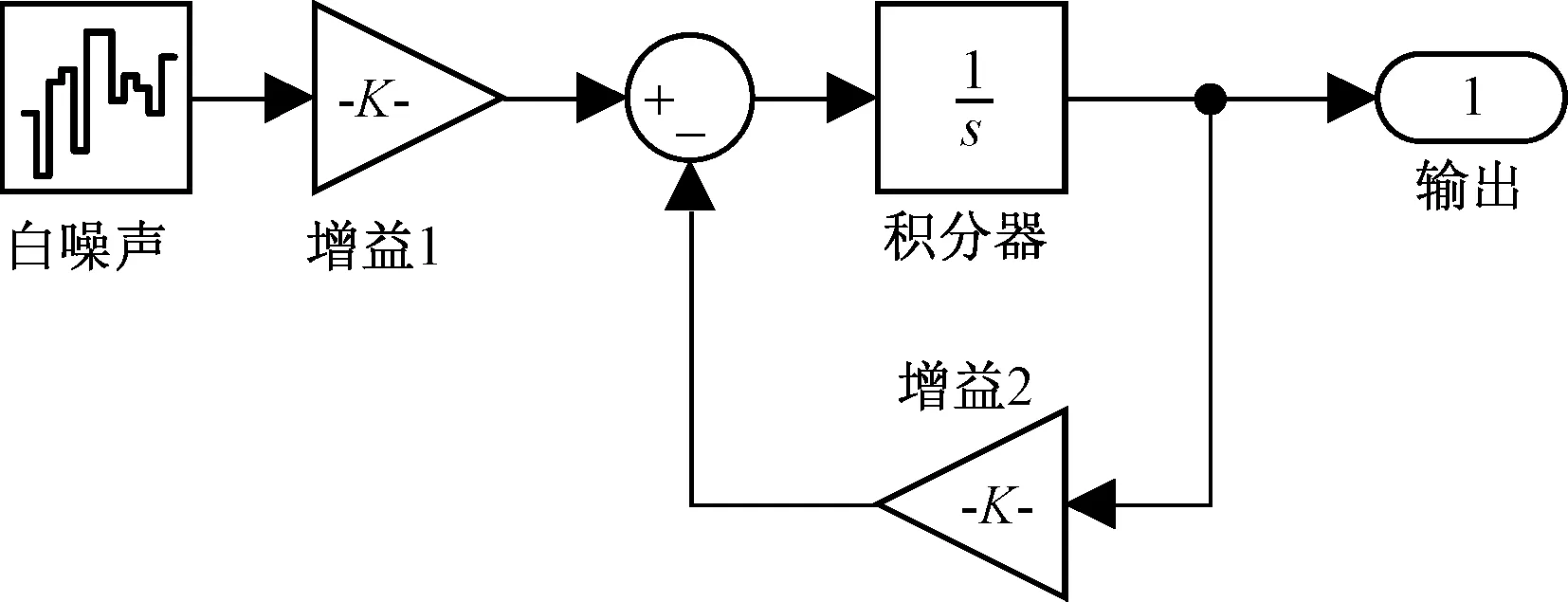
图4 路面激励仿真模型
根据式(2)所改写的系统空间状态方程建立基于模糊PID算法的半主动悬架系统模型,如图5所示。其中模糊模块主要通过模糊逻辑工具箱编写,编写完成后参考式(4)联合完成对模糊PID模块的建立,如图6所示。
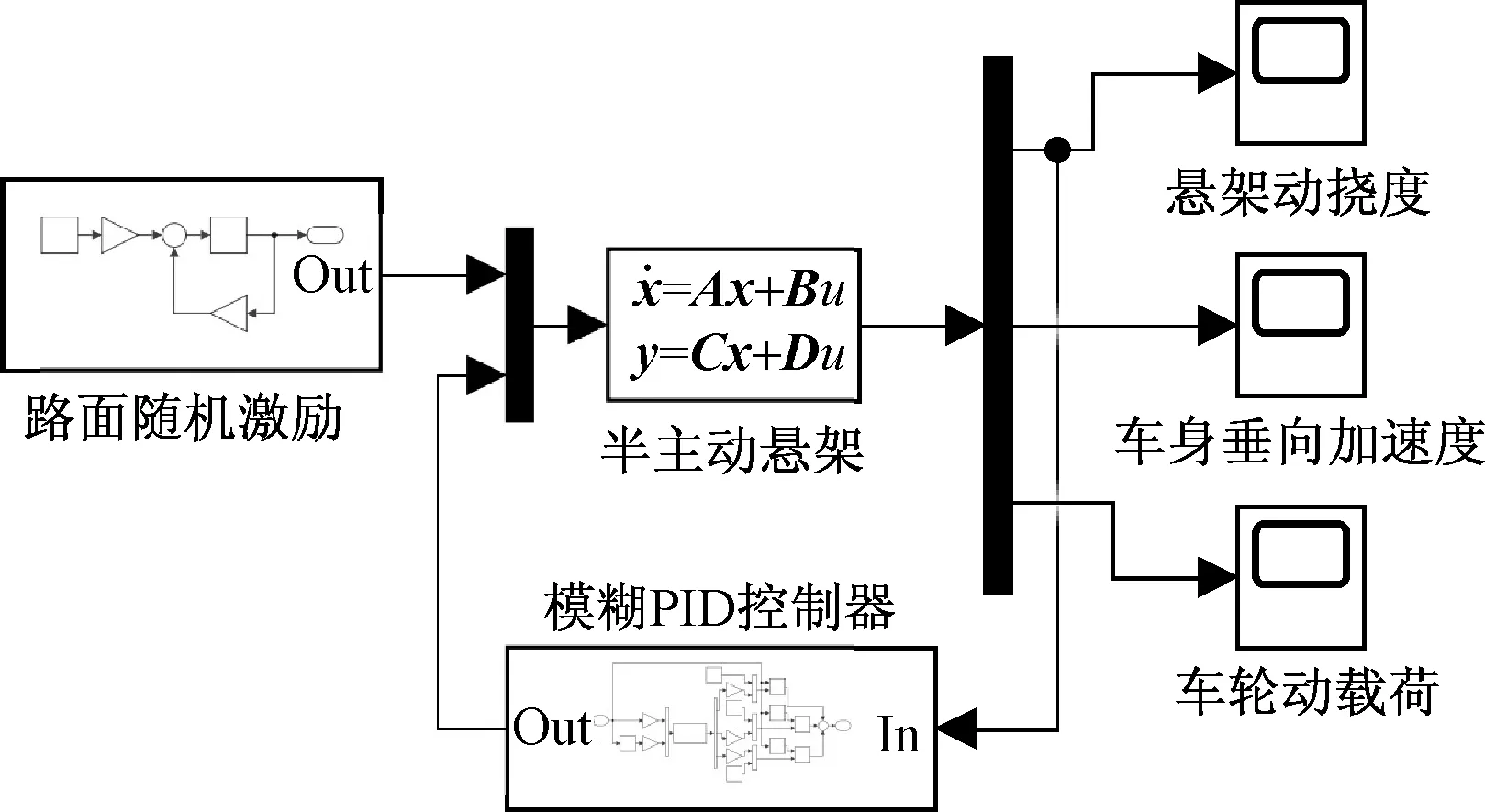
图5 半主动悬架仿真模型
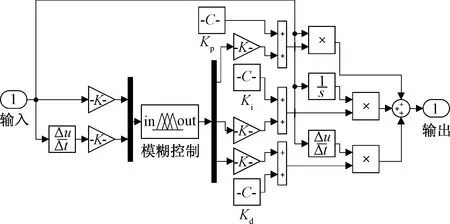
为微分;为积分;K为增益
4 仿真实例
在仿真开始前需要先对道路的垂向随机输入进行模拟,假定车辆以20 m/s的速度匀速行驶在C级道路上,模拟出的道路工况如图7所示。
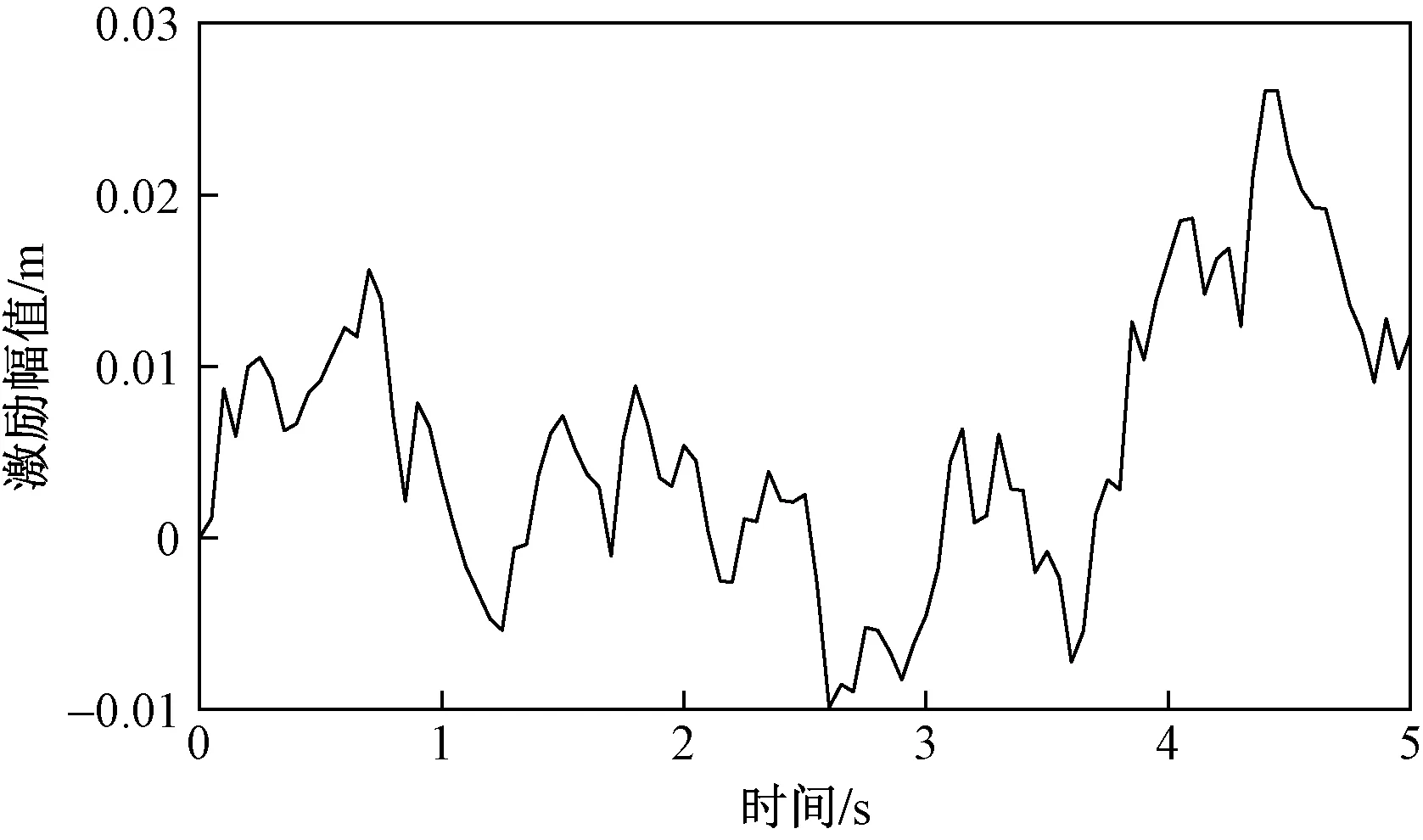
图7 路面随机激励响应曲线
选用某一车型轿车作为研究对象,其参数如下:ms=223 kg,mt=21.9 kg,ks=20 650 N/m,kt=180 000 N/m,cs=460(N·s)/m。
进行数据仿真的目的是检验所编写的模糊PID算法对悬架振动的抑制效果。因此,在同等条件下还对单纯由PID算法控制的悬架以及传统的被动悬架进行了计算及仿真。得到的3个评价指标结果如图8~图10所示。
除此之外,为了观察方便,对图8~图10曲线数据进行了均方根值计算,计算结果如表2所示。
由图8~图10可知,模糊PID算法就仿真过程整体而言可以明显减小表征悬架系统性能优劣的3个评价指标的振动峰值,尤其是在抑制车身垂直振动加速度方面效果显著,有效地抑制了由路面随机激励引起的系统弹性体的振动。单纯由PID算法控制的半主动悬架虽然在一定程度上也能表现出较好的控制效果,但在大部分仿真过程中所表现的振动抑制能力与被动悬架相差不大。这也体现了PID参数不可改变所带来的劣势,相对模糊PID算法不能根据激励大小来适当调整参数,针对振动的衰减能力较差。另外对表2中几组数据进行对比,也可以证明上述说法的正确性,模糊PID算法在对振动的抑制方面要明显优于单纯的PID算法。同时也验证了所设计的模糊PID控制器的合理性、可行性和有效性。
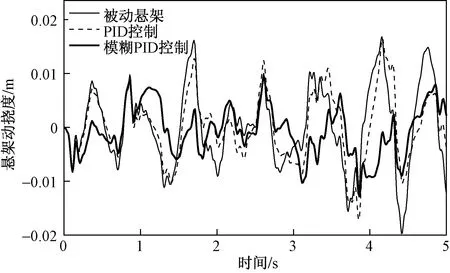
图8 悬架动挠度响应曲线
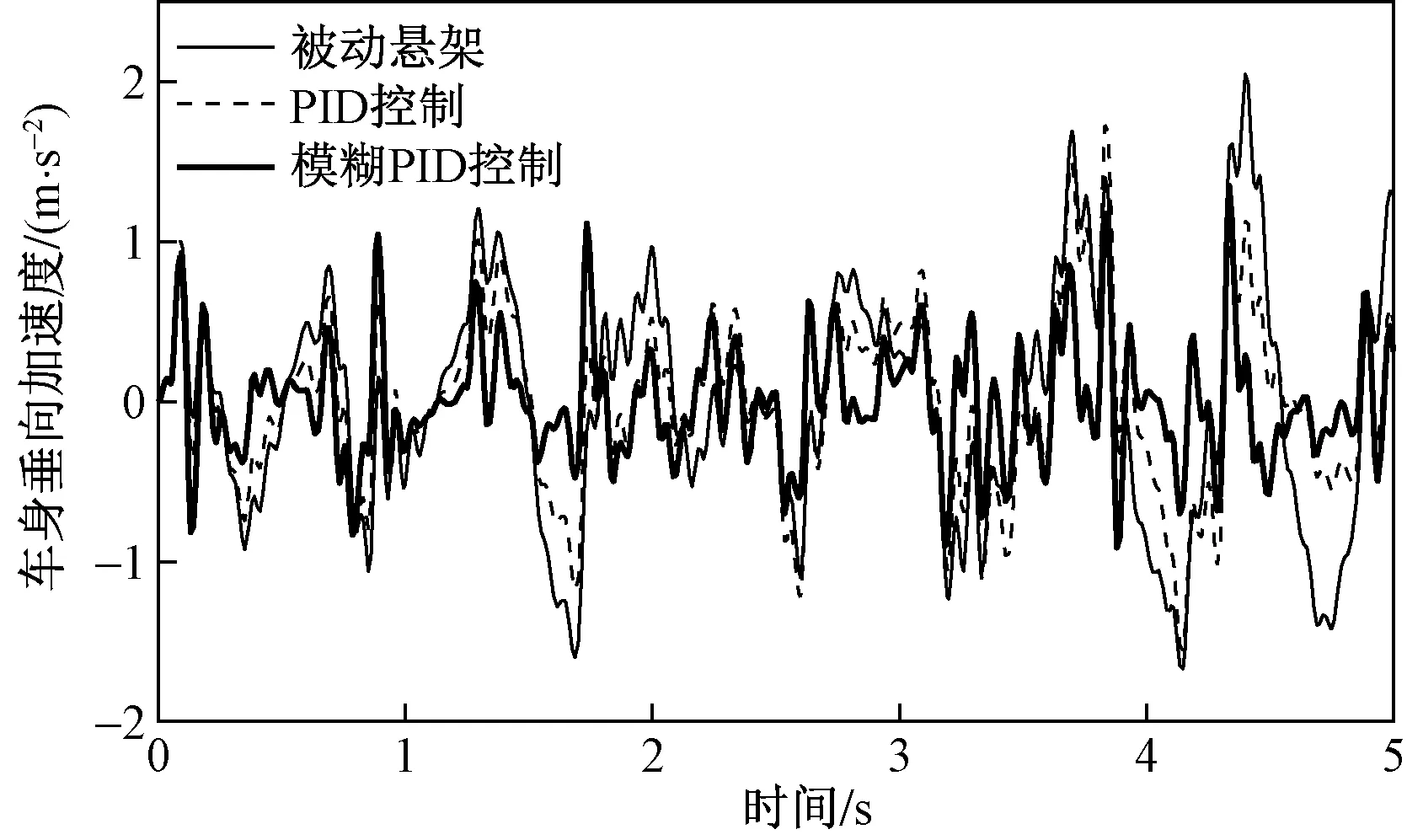
图9 车身垂向加速度响应曲线
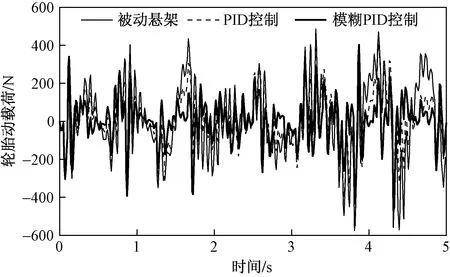
图10 轮胎动载荷响应曲线

表2 不同控制方法下悬架性能均方根值对比
5 结论
采用理论解析与数据仿真相结合的方法在1/4车辆半主动悬架模型的基础上,设计了基于模糊PID算法的半主动悬架系统控制策略。通过对比仿真得到以下结论。
(1)由PID控制的半主动悬架,在面对路面所造成的冲击时在一定程度上能够减小车身振动。但由于在运动过程中参数不可调,其减振能力与被动悬架相比并无大幅度提升。
(2)相比于单纯的PID算法,所编写的模糊PID算法针对由路面随机激励引起的车辆垂直方向的振动具有更加出色的抑制效果,有效地衰减了行驶过程中路面对汽车所造成的冲击,提升了汽车的稳定性以及驾乘人员的舒适性。
