基于预编码的正交频分复用雷达通信一体化信号设计

侯艳丽，周安敉，郭 鑫

(河北科技大学信息科学与工程学院，石家庄 050018)

雷达探测和无线通信是现代无线电技术中最重要的两个应用。随着近年来新型武器系统的研发和在军事领域中的广泛应用，现代战争已经转变为系统对抗、体系对抗[1]。为了避免装备间电磁兼容问题恶化、降低成本和减少资源占用[2-3]，针对以上问题科研人员提出了雷达通信一体化。雷达通信一体化是将目标探测系统和数据通信系统相集成，在完成雷达探测的同时完成通信数据传输，有助于实现系统设备的通用化、小型化和多功能化。同时，民用领域中雷达通信一体化可以用于智能交通和智能驾驶，实现车联网和自动驾驶，在交通运输领域具有良好的发展前景。

一体化波形的设计将直接影响雷达通信一体化系统的性能，是一体化系统设计中的重点和难点。现有的雷达通信一体化波形设计方式可以分为两类[4]：一是采用复用技术，有空分复用、码分复用[5]、时分复用[6]和频分复用[7]；二是采用信号共用技术，目前信号共用技术大致可以分为3类：基于雷达常用波形；基于通信信号；将前两者通过某种方式叠加而成[8]。对于基于雷达常用波形，可采用同调频率不同初始相位的线性调频信号实现雷达通信一体化。但是，此种雷达通信一体化波形的传输速率受限于脉冲宽度，常用于雷达探测和低速率数据传输同时工作的场景[9]。对于基于通信信号的信号共用技术，通常利用正交频分复用(orthogonal frequency division multiplexing，OFDM)信号将其改造为雷达探测波形。众所周知OFDM信号因为其优势已成熟应用于通讯领域；OFDM信号因为其时宽带宽积大，所以该信号能够应用于雷达探测[10]，并且具有低截获概率和良好的抗干扰性能。中外学者在利用OFDM信号实现雷达通信一体化方面已有大量研究，文献[11]中提出一种OFDM一体化波形，将被通信数据控制时间移位的循环移位m序列加载到相位编码OFDM(PC-OFDM)信号上，此一体化波形能够在高数据传输速率下实现目标的高分辨率距离和速度联合估计；也有许多学者对OFDM一体化信号的雷达模糊函数性能进行研究，分析和改善OFDM一体化信号的探测性能，如文献[4]在通信信息对模糊函数的影响方面进行了大量的理论推导和分析，提出了利用预调制的方法使在同脉冲不同OFDM符号间所调制的通信信息具有良好的非周期自相关和互相关特性，结果表明此方法可以降低一体化波形模糊函数对通信信息的依赖性，但是没有考虑伪随机序列长度对一体化信号模糊函数的影响。文献[12]利用合适码长的Oppermann序列对通信数据进行直接扩频，以改善OFDM一体化波形模糊函数性能，结果显示此方法可以增强一体化波形的目标探测能力，但是只考虑了Oppermann序列一种伪随机序列。

在文献[4]和文献[12]的基础上，利用具有良好相关特性的伪随机序列——m序列、gold序列和Kasami序列分别对通信数据进行预编码，得到经预编码的OFDM雷达通信一体化信号，不同程度地改善了模糊函数对通信信息的敏感性，以减弱随机通信信息对一体化信号探测性能的影响。

1 OFDM一体化信号模型

一个经典的OFDM一体化信号s(t)的表达式为

(1)

式(1)中：t表示信号持续时间；Mc为调制在每个子载波上的码元个数；Nc为子载波个数；Cn,m为调制在第n个子载波上的第m个码元；fn为第n个子载波的频率，fn=(n-1)Δf，Δf为子载波频率间隔；Tc为OFDM符号周期；rect(·)为单位矩形窗函数，可表示为

(2)

2 OFDM一体化信号模糊函数理论分析

模糊函数是设计与分析雷达波形的数学工具，用来描述雷达的分辨性能，一般的模糊函数包括4种形态：正刀刃型、图钉型、斜切刀刃型和钉板型，图钉型的模糊函数是理想型。通常根据雷达性能要求对雷达信号进行设计，所以雷达信号确定后模糊函数不再随时间变化。但是对于雷达通信一体化信号，随着时间变化所传通信信息会随之改变，进而改变模糊函数影响探测性能。推导OFDM一体化信号模型的模糊函数，分析通信数据对一体化信号模糊函数的影响。模糊函数具有多种定义方式，定义方式为

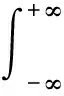
(3)

式(3)中：s(t)作为发射的一体化信号；χ(τ,fd)表示一体化信号的模糊函数；τ为时间延迟；fd为多普勒频移；s*(t)表示s(t)的共轭。

延迟时间τ后的信号s(t-τ)为

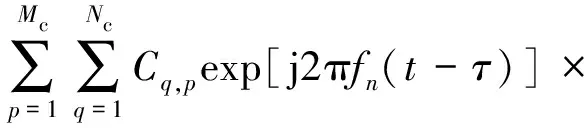
(4)

将s(t)和s*(t-τ)代入模糊函数表达式可得

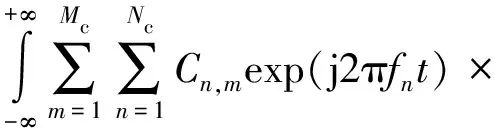
exp[-j2πfq(t-τ)]×

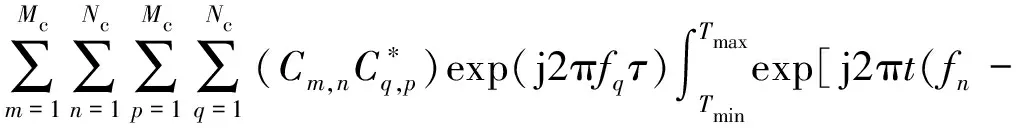
(5)

式(5)中：Tmin=max{(m-1)Tc,τ+(p-1)Tc}，Tmax=min{mTc,τ+pTc}。

因为

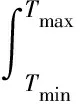
(6)

式(6)中：Tdiff=Tmax-Tmin，Tavg=(Tmax+Tmin)/2。

因此，OFDM雷达模糊函数可表示为

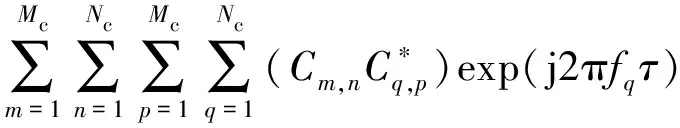
Tdiffsinc[(fq-fn-fd)Tdiff]exp[-j2π(fq-fn)Tavg]

(7)

当τ=0，fd=0时，函数取最大值为

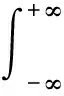
(8)

式(8)中：E为s(t)的能量。

当τ=0，fd≠0时，可得速度模糊函数为

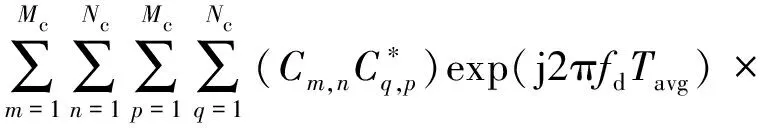
Tdiffsinc[(fq-fn-fd)Tdiff]exp[-j2π(fq-

fn)Tavg]

(9)

当τ≠0，fd=0时，可得距离模糊函数为

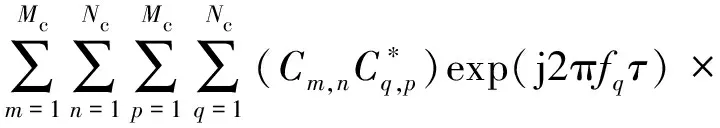
Tdiffsinc[(fq-fn)Tdiff]exp[-j2π(fq-

fn)Tavg]

(10)

式(10)中：Tmin=max{(m-1)Tc,(p-1)Tc}，Tmax=min{mTc,pTc}。

分析式(9)速度模糊函数表达式可知表示幅值的辛格函数决定了其主瓣的宽度并且通信信息不影响速度模糊函数的分辨率；而分析式(10)可知通信数据的相关性影响距离模糊函数。对于一体化波形，由于要进行通信信息的传输，而通信信息具有随机性和会随时间变化的可变性，使得通信信息会严重影响一体化信号的雷达性能。而具有良好相关特性的伪随机序列可以调节通信信息的相关性进而减小通信信息对距离模糊函数的干扰，所以利用伪随机序列对通信数据进行预编码，降低一体化信号雷达模糊函数对通信数据的依赖性。

3 伪随机序列

利用具有良好相关特性的伪随机序列对一体化信号进行预编码。首先选用应用最为广泛的m序列，m序列具有很好的自相关性，但互相关性较差，序列族数较少；考虑到不同的应用场景，同时选用了gold序列和Kasami序列。这3种序列的周期和序列族数如表1所示，其中φ(x)为欧拉数。当级数r为6，反馈系数为[1 0 0 0 0 1 1]时，产生周期为63的m序列，在m序列的基础上生成gold序列和Kasami序列。这3种序列自相关特性和互相关特性如图1和图2所示。

表1 m序列、gold序列和Kasami序列

由图1可知，m序列的自相关函数曲线没有旁瓣，而gold序列和Kasami序列自相关函数曲线旁瓣较大，并且gold序列自相关函数曲线旁瓣比Kasami序列自相关函数曲线旁瓣高。由此可得，m序列的自相关性优于gold序列和Kasami序列。分析图2可知，Kasami序列的互相关曲线较m序列和gold序列低，因此Kasami序列具有更好的互相关特性。

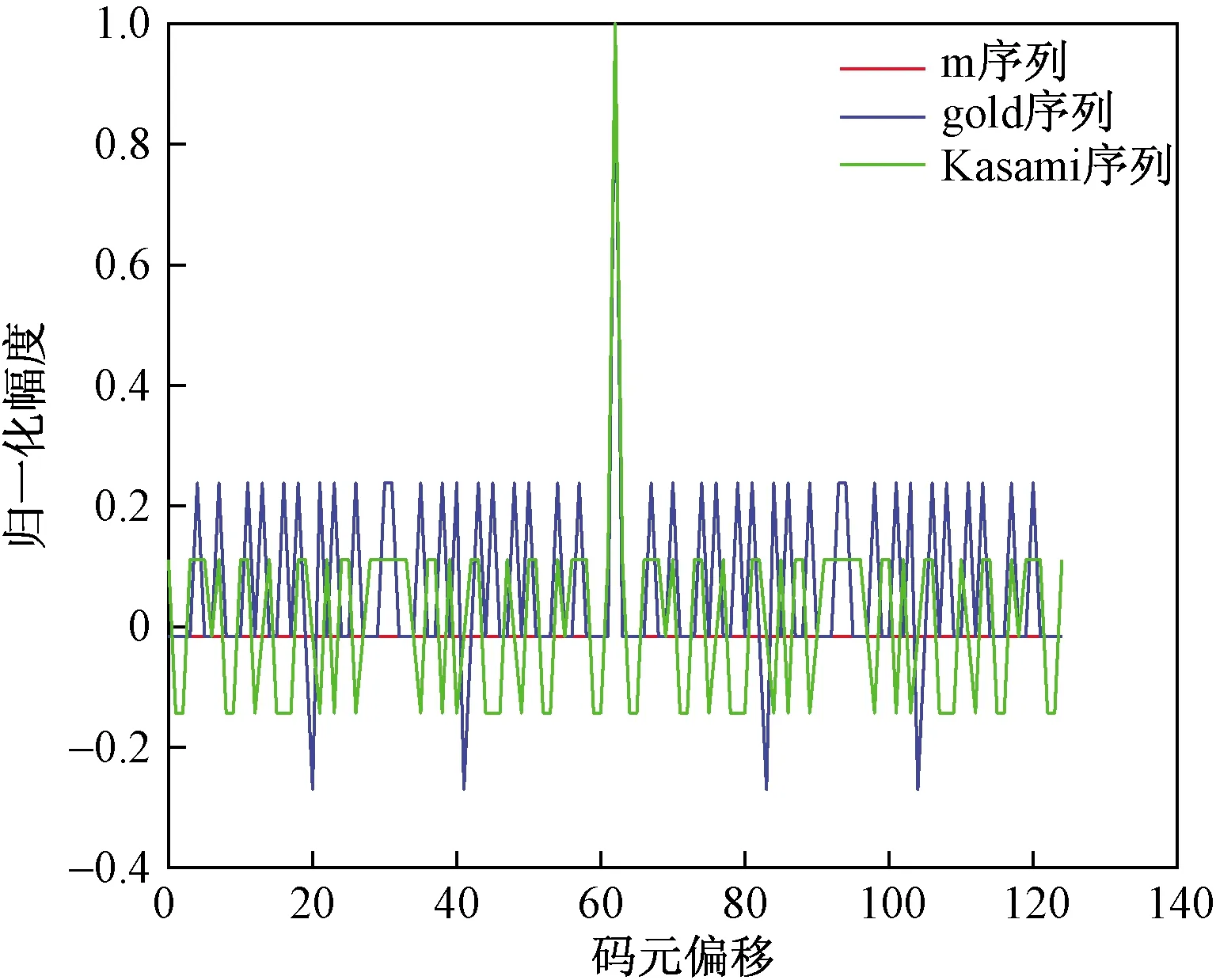
图1 自相关特性

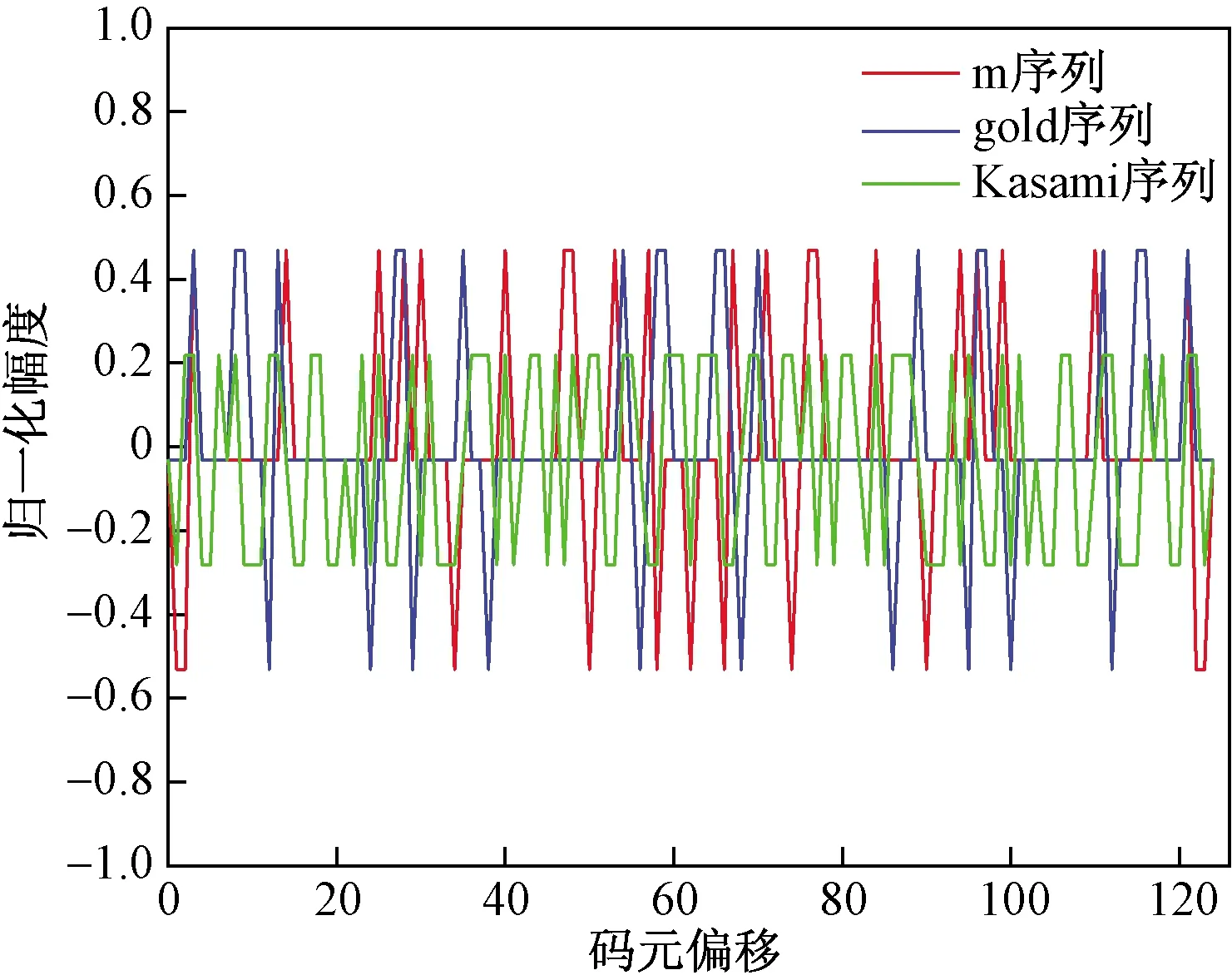
图2 互相关特性

4 仿真分析

4.1 伪随机序列对模糊函数性能的影响

仿真中OFDM信号采用16QAM调制，子载波个数设置为4，每帧的OFDM符号数设置为4，每符号上的比特数设置为4，采样频率设置为1×106Hz，一个OFDM符号的持续时间为1 μs，保护间隔与OFDM数据的比例设为1/4。3种伪随机序列的位数均为63。采用100次Monte Carlo仿真求平均值，分析其模糊函数性能。OFDM一体化信号和经过m序列预编码的OFDM一体化信号的雷达模糊函数如图3所示。通过观察对比可以发现经过m序列预编码后的OFDM一体化信号的模糊函数具有更狭窄的中心峰值，这表示采用具有良好相关特性的伪随机序列进行预编码的OFDM一体化信号具有更良好的雷达性能。

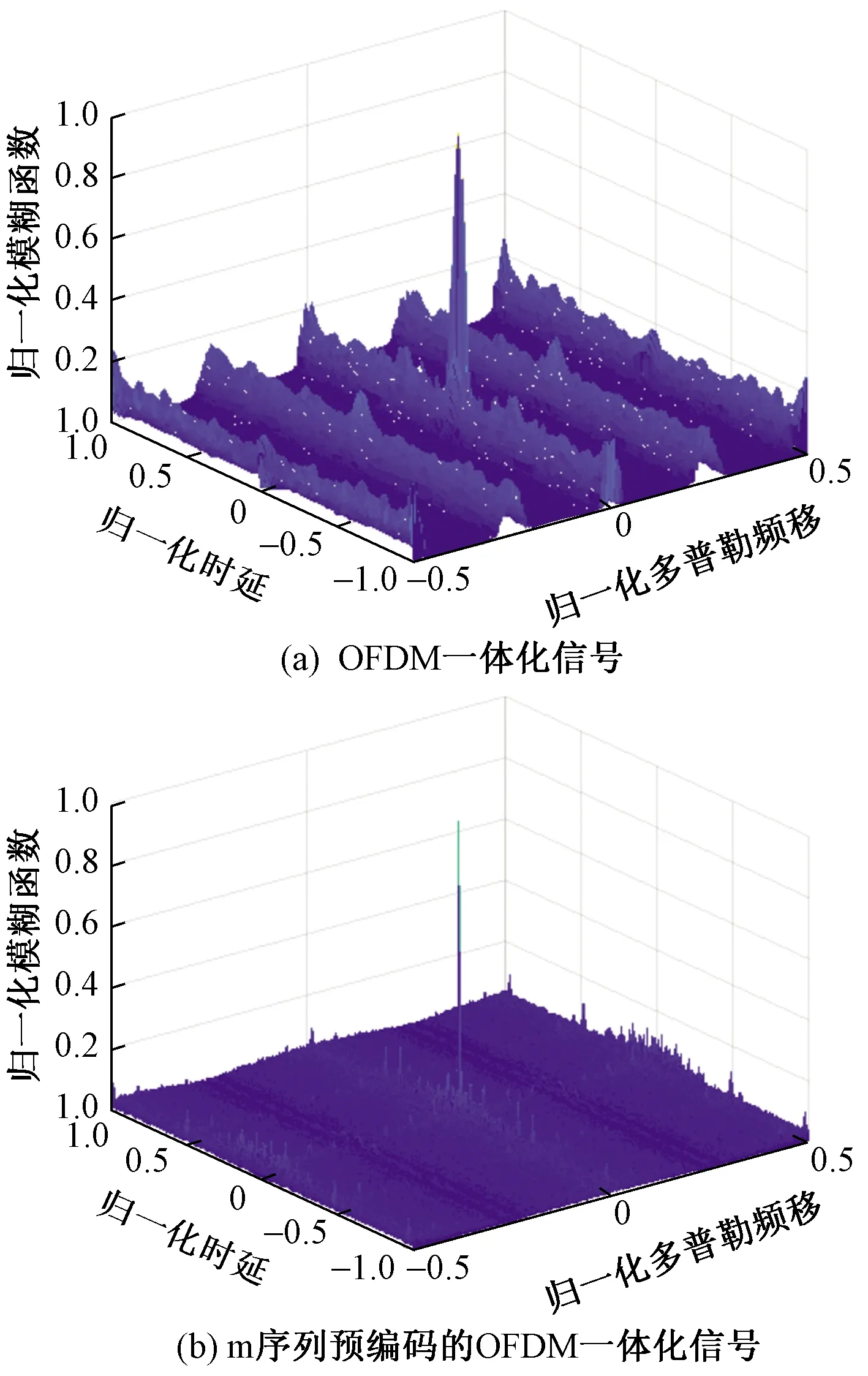
图3 模糊函数图

图4为OFDM一体化信号和基于m、gold和kasami序列预编码的OFDM一体化信号的距离模糊函数。由图4可知，采用上述3种伪随机序列进行预编码的OFDM一体化信号比OFDM一体化信号的主瓣更窄，旁瓣更低。表2为上述4种一体化信号的距离维的峰值旁瓣比，表2中显示OFDM一体化信号的距离维的峰值旁瓣比为17.50 dB，明显低于经过预编码的OFDM一体化信号，说明利用具有良好相关特性的伪随机序列对OFDM一体化信号进行预编码，能够减小通信数据对一体化信号雷达模糊函数的影响，改善OFDM一体化信号的雷达性能。

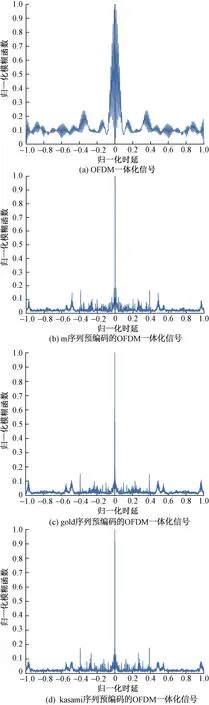
图4 距离模糊函数

表2 不同一体化信号的峰值旁瓣比

采用这3种伪随机序列进行预编码不同程度地提升了一体化信号的模糊函数性能。其中每个序列有各自的优势和不足，因此需要考虑具体的应用场景来选择具体的预编码序列。如点对点情况，具有优良自相关特性的m序列是三者中最佳的；而对于多用户的网络环境，为避免多址干扰，具有较好互相关性且序列族数较多的gold或Kasami序列将是更好的选择。

4.2 扩展因子对模糊函数性能的影响

定义扩展因子M′为伪随机序列的位数，分别为7、15、31和63。OFDM基本参数设置同4.1节。采用100次Monte Carlo仿真求平均值，分别对m序列、gold序列和Kasami序列预编码的OFDM一体化信号的模糊函数进行仿真，分析扩展因子对距离维峰值旁瓣比的影响，仿真结果如图5所示。

由图5可知，随着扩展因子M′的增加，距离模糊函数的旁瓣降低，距离维峰值旁瓣比增大。仿真结果表明扩展因子的增加可以提高一体化信号的雷达性能，但扩展因子过大会降低一体化系统的通信传输速率影响通信性能，因此应结合实际应用情况选取合适的扩展因子。

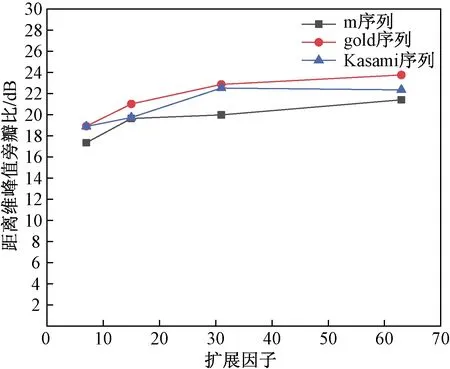
图5 扩展因子的影响结果

5 结论

针对OFDM雷达通信一体化信号中的通信信息影响其探测性能的问题，通过对OFDM一体化信号数学模型及其模糊函数的理论推导，提出一种基于预编码的OFDM雷达通信一体化信号形式。特别选取了m序列、gold序列和Kasami序列进行预编码，分析了这三种序列的特点和适用环境。仿真结果表明，取相同扩展因子时，分别采用这3种序列进行预编码，不同程度地增加了OFDM一体化信号的峰值旁瓣比，降低了OFDM一体化信号的模糊函数性能对通信信息的依赖性；随后又分析了扩展因子(M′)对距离维模糊函数峰值旁瓣比的影响，仿真结果表明扩展因子的增加可以提高一体化信号的雷达性能，但应结合实际应用情况选取合适的扩展因子。在实际应用环境中还需要考虑更多的因素以达到雷达通信一体化的要求，以此为切入点得到特性更加良好的伪随机序列进而有效改善一体化信号性能，并进行进一步的后续研究。