一种基于任意拉格朗日-欧拉方法的降落伞充气展开数值模型

2021-02-24郭琪磊

科学技术与工程 2021年2期

陈晨, 郭琪磊

(中国民用航空飞行学院，广汉 618307)

降落伞的充气展开过程历时短、变形大，是典型的复杂非线性流固耦合问题，是降落伞研究的重点和难点。近年来，流固耦合ALE方法成为解决该问题的主流方式。

文献[1-6]首先将LS-DYNA软件应用于降落伞FSI问题中，基于欧拉-拉格朗日罚函数算法，得到了初始形状为伞衣平铺展开的情况下，开伞过程中的阻力系数、摆动频率，摆动角等参数，并观察到降落伞的过度充气和循环呼吸现象，证明了该方法具有很高的可靠性和实用前景。在此基础上，文献[7-10]改进了欧拉-拉格朗日耦合算法，把伞衣的透气性参数引入降落伞的开伞模拟计算中，取得较大成功。Cheng等[11]、高兴龙等[12]和贾贺等[13-14]采用多孔介质模型研究了无限质量、不计伞重情况下，基于ALE方法的开伞充气过程，得到伞衣投影面积和有效透气性的变化规律曲线，该伞衣模型具有较真实的结构细节，如伞衣幅的突起，得到的流场数据也更加符合实际情况。马晓冬等[15]对涡环旋转伞进行了流固耦合分析与伞塔实验，得到涡环旋转伞的充气时间与开伞动载。随着研究的深入，发现基于有限质量方式建立的开伞模型更为贴近空投实际情况，其减速性能与开伞力也更受关注，但此时流入伞衣的气流速度和伞衣结构都在短时间内急剧变化，流场非稳态、流固耦合模型与降落伞系统弹道方程相耦合，求解难度较大，相应的研究结果较少。Tutt等[16]首先提出用有限质量与动网格方式建立拉直-展开下落模型，并通过实验对比，证明了该模型的正确性。高兴龙等[17]基于任意拉格朗日-欧拉(arbitrary Lagrange Euler，ALE)方法和动网格技术，建立了平面纵向开缝伞低速空投的有限质量开伞模型，得到伞衣阻力面积变化曲线，并验证了开伞动载的变化规律，最终分析了不同拉直速度对开伞时间的影响规律。Cheng等[18]、Yu等[19]基于有限元方法计算了有限质量情况下小速度开伞动载变化特征，并分析了伞衣上受载严重位置。

前人研究为数值计算降落伞空投流构耦合(fluid structure interaction，FSI)问题奠定了坚实的基础，并积累了丰富的经验，但以上计算中大部分存在一些模型假设的不合理性，如未考虑伞衣织物孔隙率、透气性影响，用无限质量模型模拟空投工况等。更为普遍的是：在降落伞拉直-展开建模计算中，大部分文献假设伞衣初始为拉直状态，并设拉直速度为初始速度。但实际工况中，初始投放瞬间，伞绳上并未加载初始应力，初始不处于张紧状态(即尚未拉直)，这与实际工况不符，导致模型计算的拉直速度、下落距离和拉直/开伞时间有一定误差。

为完善数值计算模型，拟基于ALE方法和动网格技术，考虑织物透气性并预设初始投放速度，建立降落伞充气展开的有限元模型。以C-9型伞作为算例，计算充气过程中，有限质量情况下的开伞力，并与实验数据对比，拟通过实验验证该模型的正确性与合理性，随后分析其开伞过程中应力分布特征与气动减速特性。预期为降落伞数值分析和设计提供参考依据。

1 数学模型

1.1 模型假设

(1)降落伞伞衣初始为折叠状态，伞绳为近似拉直状态。

(2)忽略伞衣织物摩擦力的影响。

(3)由于降落伞投放区域海拔不高，且运动速度小于0.3马赫数，可忽略空气的压缩性，用时变非稳态不可压流模拟流场特性。

1.2 材料本构模型

1.2.1 伞衣模型

柔性织物在展开过程中可看作线弹性各向同性材料，则根据弹性力学理论，其本构方程为

σij=λεkkδij+2ϑεij

(1)

式(1)中：σ为应力张量，σij为σ的分量；ε为Green应变张量，εkk、εij为ε的分量；δij为Kronecker记号；λ和ϑ为拉梅常数，可以由材料的杨氏模量(E)和泊松比(υ)计算，其计算公式为

(2)

(3)

用三节点壳单元模拟伞衣织物，则根据平面应力假设和材料对称性假设，式(1)可简化为

(4)

1.2.2 空气模型

理想气体状态方程结合流体本构方程模型可建立流体域计算模型。其中理想气体状态方程为

p=(1-γ)ρωint

(5)

式(5)中：p为静水压力；γ为气体比热；ρ为气体密度；ωint为气体单位质量内能。

(6)

式(6)中：v为运动速度，vi,j、vj,i为v分量；μ为动力黏性系数。

1.2.3 伞绳模型

用一维线弹性本构方程计算伞绳拉力：

F=Kmax(Δl,0)

(7)

式(7)中：Δl为绳长变化量；K为材料刚度。

Δl=l-(l0-loff)

(8)

(9)

式中：l为伞绳当前长度；l0为伞绳原长；E为绳索弹性模量；A为绳索截面积；loff为偏移量，模型中伞绳初始无预应力，即为松弛状态，故设偏移量为负值。

1.3 控制方程

用ALE方程求解自由界面流动及典型的流固耦合问题。具有物质运输功能的单元在两种坐标体系的网格间平动，在耦合界面处流体节点随结构变形运动。将流体质点速度通过质量守恒和动量守恒定律在黏性不可压流体域内离散。

1.3.1 结构动力学模型

伞衣织物是柔性大变形体，具有强非线性动力学特征。令Ωs为空间结构域，固体边界用∂Ωs表示，可得结构控制方程，在固体边界∂Ωs上[20]有

(10)

式(10)中:y为位移矢量；ρs为结构材料密度；f为作用在结构上的体积力；σs为结构体Cauchy应力张量;t为时间。

1.3.2 流场动力学模型

ALE方程描述中，在参考坐标系下，不可压流体的纳维-斯托克斯方程(Navier-Stokes,N-S)方程为

(11)

(12)

(13)

式中：u为流体速度；w为参考构型下网格点的移动速度；ρf为流体密度；e为物质内能。对于牛顿流体，应力张量(σf)定义为

σf=-pI+μ[gradu+(gradu)T]

(14)

式(14)中：p为压力；I为二阶单位张量；μ为动力黏度系数。

其中，Dirichlet和Neumann边界条件为

(15)

(16)

u(x,0)=u0

(17)

式(17)中:u0为初始来流速度。

1.4 耦合方式-罚函数法

伞衣与流体域的流构耦合要求在建立有限元模型时，结构与流体的网格可以重叠在一起，但又能实现力学参量的传递，使用罚函数法。追踪在任意tn时间步内，拉格朗日节点(结构节点，从节点)和欧拉流体物质(流体节点，主节点)位置间的相对位移dn，主从节点的相对速度为vrel，则dn的迭代更新方程为

(18)

耦合界面上的力与发生的贯穿数量成正比：

Fn=kidn

(19)

式(19)中：ki表示基于主、从节点质量模型特征的刚度系数。

1.5 透气性

伞衣为柔性透气织物，具有渗透性，其耦合力可通过薄膜状Shell单元体积的Ergun方程导出得[12]

(20)

式(20)中：r为伞衣单元的法向；a(μ,ε)为渗透性Shell单元的渗透系数(黏性系数)；b(ρ,ε)为惯性系数；a、b组合反映了织物的透气性特征[14]。

1.6 初始投放速度

在降落伞初始空投时，初始投放速度并不等于拉直速度。初始投放时，伞衣和重物速度相等，重物受的空气阻力小，运动速度较快，到达某个位置后具有相对伞衣的最大速度差Δvmax，在此位置，伞绳被绷紧并开始拉伸。当伞绳拉直时，伞衣被重新加速，以致在此瞬间伞衣与重物的速度差Δv=0，而伞绳的黏弹性伸长度已吸收了减速器的全部动能后，轴向张力载荷出现瞬时峰值，即拉直力，而此时伞衣和重物的速度才是拉直速度。

根据Wolf提出的最大速度差估算方法预估投放初始速度[21]：

(21)

(22)

(23)

式中：Δvmax为伞衣相对回收体的最大速度差；v0为初始投放速度；f为拟合曲线斜率；ρ为空气密度；(CDS)p为伞衣的阻力面积；l1为伞绳初始长度；mp为减速器质量；mc为伞衣质量；m1为伞绳质量；Kb为系数，表示不同工况，可从文献[21]中读取；CDA为重物阻力面积；mb为重物质量；vb为伞绳拉伸时重物速度。

根据式(21)～式(23)预估的初始投放速度可能由于伞型、有无吊带、降落伞质量分布等因素影响与实际情况稍有偏差，需通过试算调整初始投放速度，获取真实值。

2 计算模型

以C-9型伞作为算例，建立全尺寸数值模型，计算其空投自由下落→充气→开伞(折叠展开)→稳定下落的整个过程，重点关注充气展开阶段。模型参数如表1所示。

表1 降落伞模型参数

降落伞下悬挂重物(载荷)，以90°的轨迹倾斜角空投，具体工况如表2所示。

表2 空投实验工况

由于不考虑悬挂载荷的气动特性，为简化计算，用一个长方体板壳结构模拟重物。带有伞顶孔的降落伞折叠模型网格(图1)，其中包括伞衣、伞绳和重物，伞绳处于未完全拉直状态，无初始预应力。为模拟有限质量情况下的空投过程，用动网格技术追踪降落伞，所建立的流体网格域如图1所示。伞衣位于流体域的中下部，在伞衣附近加密流场网格，且等比放大填充整个流体域，以优化计算效率。考虑伞衣织物透气性，基于显式有限元方法，采用二阶精度的Van Leer MUSCL格式求解控制方程。

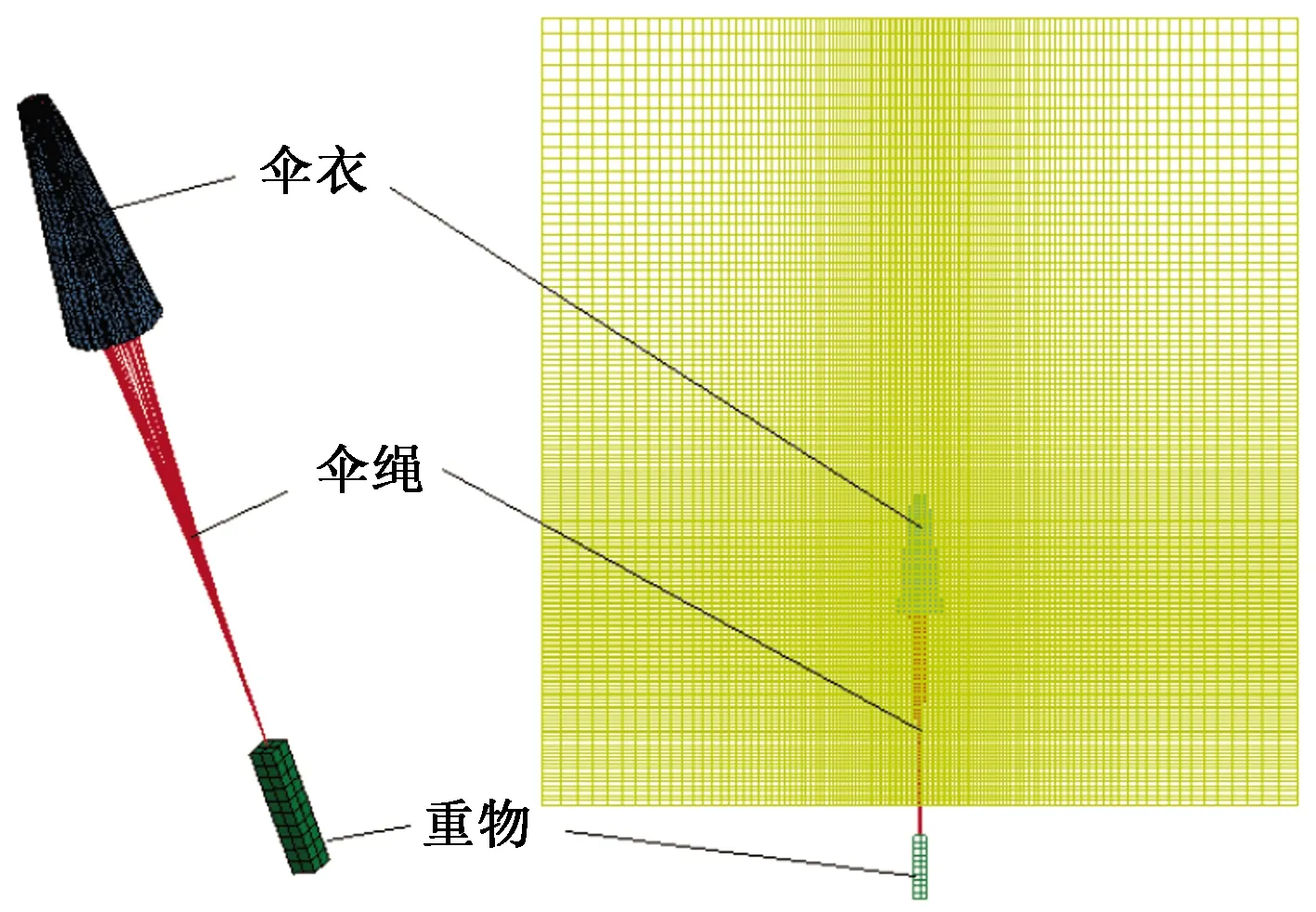
图1 降落伞及流场域模型

3 结果验证

计算结果与空投实验结果[21]对比如图2所示。图2中，F为开伞力，Wb为重物重力，t为时间，tf为伞衣充气时间。从图2可知，计算的开伞力与实验结果吻合较好：开伞时间基本一致；开伞力变化趋势基本相同；开伞力有两个峰值，且其出现时机基本一致。但计算值的开伞过载整体偏大，且比实验稍有提前，这主要是由于伞衣结构模型未能充分考虑阻尼耗散与摩擦力的影响造成的。两条曲线中比较明显的区别是，计算曲线在t/tf=0.25出现明显冲击载荷，而实验值没有，这正是数值模拟计算中体现了拉直力的作用。在设计和实际投放降落伞时，都已采用了引导伞或开伞袋来抵消拉直时的猛烈冲击，而本模型计算中并未考虑此项，而是采用直接拉直的方式，从而反映未作任何设计时，拉直力的大小与拉直时间。

图2 开伞力随时间的变化曲线

参考文献[21]中的另一算例中，给出了拉直力和开伞力间的关系，由于实验工况未明，只有拉直力与开伞力的峰值与变化趋势可参考。将计算结果中拉直瞬间作为时间零点绘制图3。

图3 拉直力与开伞力间的关系

Fs-test表示实验中拉直力峰值，F1-test表示开伞力峰值，Fs-cal表示计算拉直力峰值，F1-cal表示开伞力峰值。从图4可得，实验结果中，Fs-test/F1-test=0.83，而计算结果中，Fs-cal/F1-cal=0.8，相对误差为3.6%，属于工程可接受误差范围，这也证明了本文模型的正确性。

图4 折叠开伞过程中的应力分布

4 结果分析

4.1 折叠开伞过程

随着时间的变化，开伞过程与应力分布如图4所示。其中零时刻为投放时刻。

0时刻，投放伞体，伞衣折叠，与重物一起自由落体下降。0.015 s伞衣底口张开，空气质量开始以气团的形式进入伞衣内部，并沿伞衣运动。0.02 s时少量气团首次到达伞衣顶部。0.045～0.075 s时，气团继续汇聚，扩大伞衣内部，伞衣因径向动量而膨胀，而伞衣底边面积基本保持不变。最大应力出现在伞绳连接和伞顶处，前者是受伞绳拖曳力的影响，后者是受气团附加质量力的影响。0.075 s时，更多气团到达伞顶，一小部分从伞顶孔逸出，伞衣从底边充满到伞顶，大部分形成空气附加质量，拉伸伞绳，伞绳受力伸长，伞衣受伞绳、重物和空气附加质量的影响，形成瞬间拉直力的峰值，此时拉直速度为76.2 m/s，最大应力在伞衣与伞绳连接处。0.095 s时，更多气流汇聚到伞顶孔处，伞顶膨胀，应力大多集中在顶孔附近。随后，在0.095～0.185 s，空气质量开始沿伞衣流管充入伞衣内部，除伞顶外的伞衣也逐渐膨胀，此时，伞衣周向受力基本均匀分布，整个降落伞的下落速度也趋于稳定，最大应力仍集中在顶孔和伞绳连接处。0.185 s时，大量空气质量团首次汇聚到伞顶孔处，形成“乌贼状”伞衣，代表着充气过程中最初阶段的终结，也形成了开伞作用力的第一个峰值，顶孔褶皱处有少许应力集中。0.185 s后，降落伞减速效果明显，伞衣径向膨胀速度加快，顶孔和伞衣上部应力不断增大，受气流与织物耦合力的影响出现应力不对称、形状不对称等开伞过程(0.285 s)，但随着时间推移，受气动力影响，这种不对称被减弱乃至消除(0.335 s)，伞衣趋向于均匀膨胀，顶孔处伞衣完全展开，应力逐渐减小，伞衣上部应力逐渐增大，应力集中部位也由顶孔处转移至伞衣上部褶皱处。0.4 s时，伞衣投影直径(Dp)/伞衣名义直径(D0)=0.58，接近完全张满，此时，出现开伞力的第2个峰值。随着伞衣膨胀，伞衣中部应力逐渐增大而顶部减小，柔性织物不规则变形，褶皱处出现最大应力(参考0.41 s时)。在0.435～0.475 s时，Dp/D0为0.67～0.7伞衣充满[21]，伞衣周向应力趋于平均，仅褶皱处存在应力集中，随后随着伞衣膨胀逐渐消失。之后，伞衣继续稳定下降，空气附加质量趋于恒定，出现轻微的呼吸现象，伞衣提供的稳态气动阻力使重物减速下落(图5)，图5中，横轴为时间t(s)，纵轴为伞衣和重物的下落速度V(m/s)。随后，周围空气质量的动量造成伞衣底边过度扩张膨胀和伞顶塌陷(0.55 s后)。

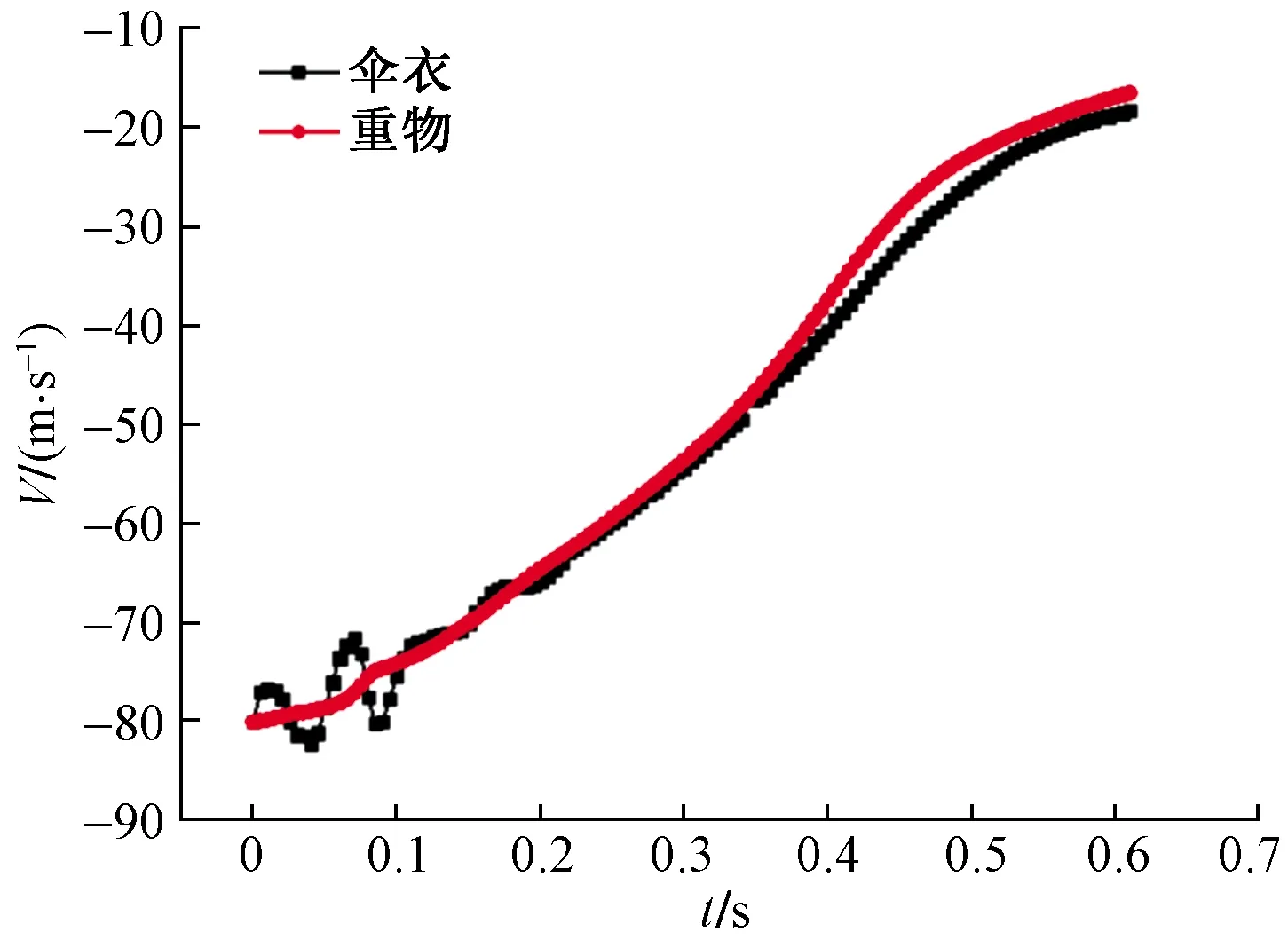
图5 伞衣及重物运动速度变化曲线

4.2 伞衣周围流场

开伞过程中，值得注意的是5个典型阶段，即拉直→充气→乌贼状→膨胀→充满，此时伞衣周围流场变化如图6所示。

图6 伞衣周围流场变化

0.045 s时，气流由伞底流向伞顶，并从顶孔加速逸出，在顶孔处形成扇形低压区，诱导更多气流从伞底进入伞衣流管内部，伞底处形成入流涡。0.075 s时，伞绳拉直，更多气团到达伞衣顶部，并在顶孔周围汇聚、加速，形成伞衣内外较大压差，顶孔处的气流稳定流出，形成尾迹，而此前形成的扇形低压区逐渐减弱消失。有少量气体从伞衣织物表面逸出，体现了伞衣的透气性特征。0.125 s时，伞衣内部气流加速，形成径向动量，膨胀整个伞衣，伞衣周围气流在结构的作用下形成数个涡，引起伞衣结构瞬间非线性大变形，而结构同时影响涡的位置的大小。相对的，顶孔处的尾流更加流畅和稳定。0.185 s时，伞衣呈“乌贼状”，结束充气过程的最初阶段，伞顶的涡在伞衣外形和压力梯度变化的作用下脱落，形成非对称尾迹，这与文献[20]结论相同，也符合钝体扰流尾迹特征。0.285 s时，伞衣在气动力和惯性力的作用下继续膨胀并左右轻微摇晃，伞衣周围气流在伞衣结构作用下被加速，产生附加质量力，尾涡加速形成和脱落。0.4 s时，伞衣周围气流扰动加强，阻力面积增大，开伞力达到峰值，尾迹也形成规律的周期性脱落涡。0.455 s，伞衣充满，伞衣内部径向动量趋于消失，周围气流也趋于稳定，形成有效阻流体，尾迹涡继续周期性形成并脱落，并且更加稳定和强烈。0.55 s后，伞衣过度扩张，伞顶附近的涡破碎分离，气流动量引起伞顶塌陷，但整个系统依旧保有减速回收效果。