基于分数阶积分的发动机在线检测数据融合技术
2021-02-24左延红左承基方继根
左延红, 左承基, 方继根
(1.安徽建筑大学机电工程学院, 合肥 230601;2.合肥工业大学机械工程学院, 合肥 230009)
随着中国国民经济的发展,汽车已走进千家万户,汽车故障导致交通事故的频繁发生,使得人们对汽车的安全性提出了更高的要求。信息技术的发展,特别是“物联网+”理念的提出掀起了汽车行业的第四次技术革命。应用物联网技术实时采集汽车核心部件的运行参数,实现汽车各核心部件的在线监测与故障诊断技术,已成为当前汽车行业研究的重点课题。作为汽车的“心脏”,发动机无疑是汽车中最为重要的部件。因此,应用物联网技术实现汽车发动机的在线监测和故障诊断已成为汽车行业专家学者们研究的重要课题[1]。物联网下的汽车发动机在线监测与故障诊断系统,首先应用汽车车载传感器系统进行信号采集工作,然后通过无线网络将采集到的各类信息(如转速、油温和噪声等)发送给数据处理中心,数据处理中心将处理后的信息数据发送给的专家系统,专家系统分析这些信息数据后向系统实时反馈发动机的运行状态信息。在当前的计算机技术下,应用物联网技术在线采集发动机各类信息已经不是难题[2],但由于汽车在行驶过程中,发动机的工作条件不稳定,部分零件的工作环境恶劣,加上受信息采集时设备性能和信息远程传送中能量损失等多种因素的影响,系统远程采集到的发动机信息数据存在着难以预测的检测误差,从而直接影响着专家系统工作的可靠性。因此,如何有效消除汽车发动机各类信息数据的远程测量误差,已成为当前开发物联网下汽车发动机远程监测和故障诊断系统的技术瓶颈。
数据融合技术是近几年来发展起来的一门实践性较强的应用技术,应用各种算法对系统收集到的信息数据进行融合处理,故具有成本低廉、准确性较高的优点,而被广泛应用于工业、军事、交通和金融等领域[3]。近年来,多位专家学者探索应用数据融合技术来提高汽车发动机检测系统工作的准确性,并取得一定的研究成果。文献[4]中应用神经网络及其改进算法融合处理汽车发动机转速、油耗的测量数据;文献[5]中应用基于最大隶属度的多传感器数据融合算法融合处理发动机转速和冷却水温的检测数据;文献[6]中应用模糊优选模型、神经网络模型和灰色关联度模型融合处理发动机磨损检测数据判断发动机磨损状态。但这些研究成果应用在物联网下汽车发动机检测数据的融合处理中,存在以下不足:文献[4]尚处于计算机仿真阶段缺乏实验的真实性,文献[5]未考虑到发动机检测信息远程传输过程中会受到信号干扰和能量损失等影响因素;文献[6]中介绍的融合算法计算过程过于复杂且具有应用范围的局限性。以上文献中算法无法应用于数据级的多传感器检测数据的融合处理之中。为此,应用分数阶积分算子融合处理物联网技术下汽车发动机的远程检测信息数据,并通过对发动机油温的在线远侧检测数据融合处理实例验证算法的准确性和实用性,为提高物联网下汽车发动机在线监测故故障诊断系统工作的可靠性和决策的科学性提供理论上的支持。
1 分数阶积分算子
1.1 分数阶积分算子的定义
分数阶积分属于分数阶微积分理论的一部分,而分数阶微积分理论是从整数阶微积分拓展而来,学术界尚未形成一个统一的分数阶微积分的时域定义表达式,在基本理论研究和工程应用研究领域,常用的分数阶微积分定义有Grunwald-Letnikov、Riemann-Liouville和Caputo Riesz[7]。3种定义中因Grunwald-Letnikov定义容易改写成函数与相应权值的卷积运算形式,具有计算过程相对比较简单的优点而被广泛应用于信息处理领域。故应用Grunwald-Letnikov定义下的分数阶微积分理论融合处理汽车发动机的远程检测信息。
分数阶微分的Grunwald-Letnikov定义为:对于任意实数v,记v的整数部分为[v],假设函数S(t)在区间[a,t]上有n+1阶连续导数,v>0时,n≥[v],则定义信号S(t)的v阶微分为

(1)

(2)
在分数阶微积分的计算中,分数阶微分和分数阶积分互为逆运算。故将式(1)、式(2)的阶次从正实数推广到负实数,即令w=-v、J=D-,便可得到S(t)的w阶积分的最终表达式。

(3)
1.2 分数阶积分算子在信号处理中的应用特性
随着人们对分数阶微积分理论与应用技术的研究的深入,发现分数阶微积分理论具有适合于研究具有非线性、非因果、非平稳等特征的不确定信号的优点,并研究出许多非常适合在现代信号分析与处理中应用的基于分数阶微积分理论的经典算法[8]。作为分数阶微积分理论之一,分数阶积分算子以其特有的信号处理特性被广泛应用于信号处理领域中,且取得了丰硕的研究成果。文献[9-11]将分数阶积分算子应用于图像去噪技术中;文献[12-13]将分数阶积分算子应用远距离检测目标的识别与检测技术中;文献[14]将分数阶积分算子应用于感应电机的速度控制技术中。探讨分数阶微分算子在信号处理中的应用特性。
假设在工程实践中信息采集系统采集到一平方可积的能量信号S(t),且S(t)∈L2(R),则可对信号S(t)进行Fourier变换得
(4)
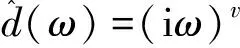
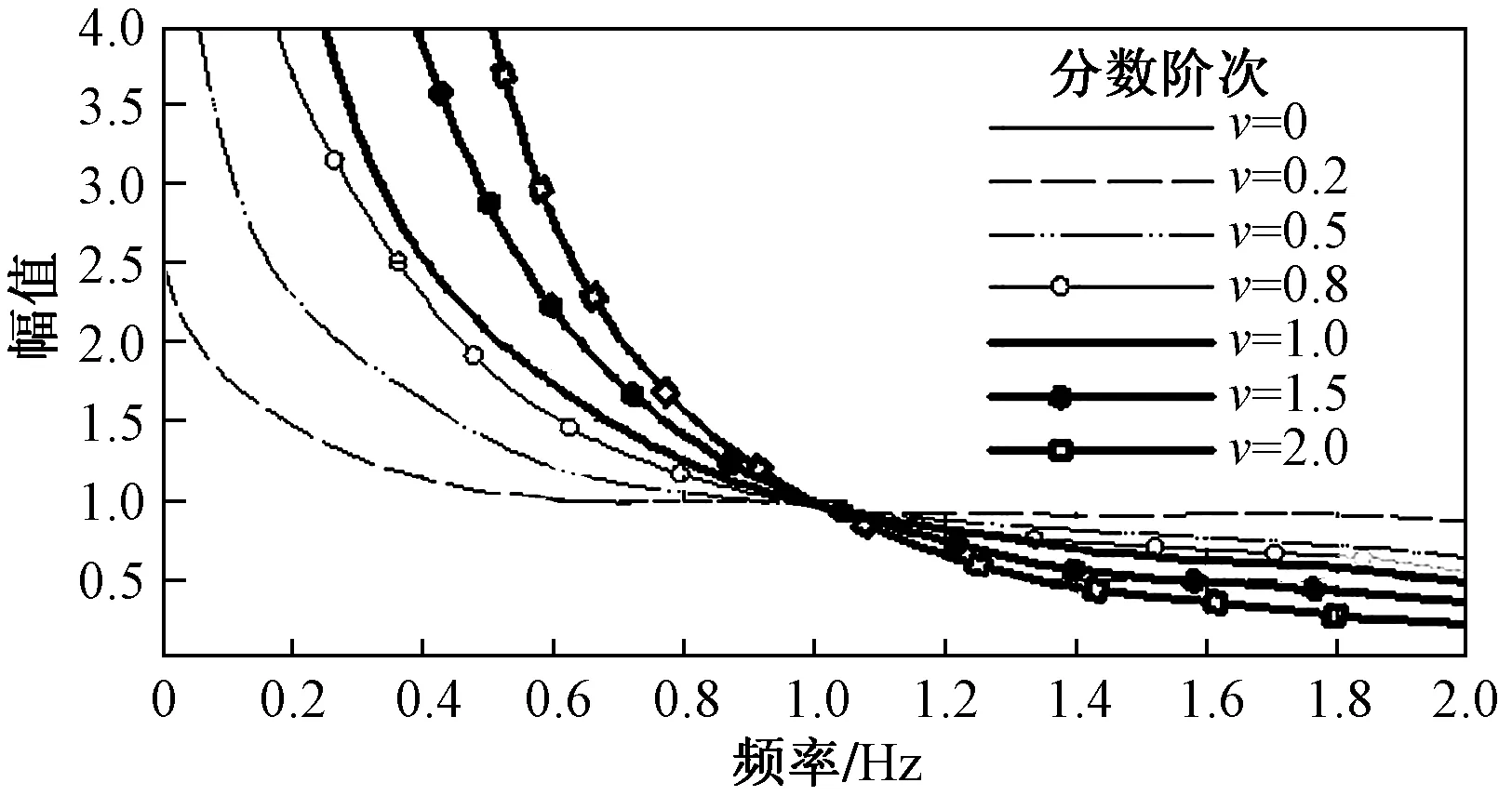
(5)

(6)
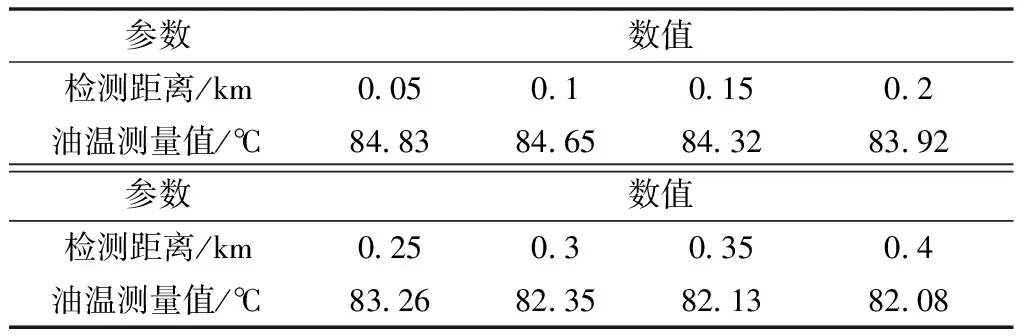
根据分数阶积分算子与分数阶微分算子互为逆运算的理论,取J=D-,w=-v(-1 (7) 从图1特性可知,分数阶积分算子在有效削弱信号高频部分信息强度的同时,实现了信号最高频部分的非线性保留;在有效增强信号低频部分的同时,也实现了信号最低频部分的一定程度上的保留。 图1 分数阶积分算子的幅频特性曲线 能被物联网下汽车发动机在线监测与故障诊断系统远程检测的信号一定为能量信号,信号E(t)可以是发动机的油温、转速、噪声和振动等任意类型的检测信号。假定信号E(t)的测量值为Ei(i=1,2,…,n),因汽车在运行过程中发动机的工作环境恶劣,以及信号E(t)远程传送带来的能量损失,致使系统采集到的信号值Ei与测量真值间存在着难以预测的检测误差。信息测量误差主要来自检测系统中检测仪器性能等内在影响因素和工作环境等外在影响因素,但在汽车发动机信息的远程采集系统中,系统硬件设施的性能在短期内基本上不发生变化。而汽车在运行过程中发动机的工作环境和信号传输距离等外在影响因素则处于时刻动态变化中,致使外部影响因素带来的测量误差因无规律可循而成为信号远程检测技术面临的难题。应用基于分数阶积分算子的检测数据融合算法解决以上技术难题,假设发动机的工作环境和信号传输距离等外在影响因素为信息测量值的影响因子x,这样就可用MATLAB软件找出影响因子xi与Ei之间的关系式E(x),x∈(a,b),其中a、b分别为影响因子x的最小值与最大值。 根据分数阶微积分的Grunwald-Letnikov定义,先将发动机远程检测信息测量值E(x)的影响因子x的持续区间(a,b)按步长(h)均分,则计算步数n=(b-a)/h,可得Grunwald-Letnikov定义下函数E(x)关于影响因子x的分数阶积分方程为 (8) (9) 将式(9)代入式(8),可得基于分数阶积分算子的物联网下汽车发动机远程检测信息的数据融合算法模型: (10) (11) 汽车发动机在线监测与故障诊断系统首先应用物联网技术实时收集安装在汽车发动机上的各类前端监测传感器测得的发动机各类参数信息数据,再采用分布式系统下的积分思想[16]对所采集的信息进行分类,评判同类信息数据的检测质量。如果采集的同类信息数据间的差异性超过了系统设置的公差范围,则说明外在影响因素对检测信息测量值的影响比较明显,导致检测信息的测量值严重失真,需要对检测信息进行有效的融合处理以确保系统工作的可靠性。差异性检测数据间的融合处理过程如图2所示。 步骤1 应用物联网技术实时采集汽车发动机在工作中产生的各类监测信息(如转速、油温、噪声和振动等影响发动机运行状态的重要信息)并将其分类处理。 步骤2 评判信息采集系统在不同时刻采集到的同一检测信息数据之间的误差是否在检测系统设定的误差范围内,如在误差范围内,可将检测数据直接发送至系统的数据中心,否则进入下一步。 步骤3 根据检测信息的数据特征,选取对检测信息测量值具有较强影响力的影响因素作为外在影响因子x;综合发动机检测信息在影响因子数值xi时的测量值Ei,应用MATLAB软件拟合出测量值Ei与影响因子xi之间的函数关系式E(x)。 步骤6 融合后的检测数据传送给汽车发动机在线检测与故障诊断系统的数据中心,汽车发动机在线检测数据分数阶微分融合处理过程结束。 汽车发动机在线监测与故障诊断系统的正常工作需要实时采集发动机在运行中产生的油温、转速、噪声和振动等多类型信息数据,因每类信息数据的融合处理方法与过程基本相同,受篇幅所限,只研究发动机运行中重要检测信息——油温的分数阶积分算法融合处理过程与效果。机油在发动机的运行过程中起到润滑减磨、辅助冷却降温、密封防漏、防锈防蚀、减震缓冲等作用。被誉为汽车的“血液”。汽车发动机在正常运行过程中,机油的正常工作时的温度比较稳定,一般70~90 ℃,如果速度快,温度可以达到100~110 ℃,如果机油温度长时间超过120 ℃,就会失去其润滑、清洁、散热的作用,严重时会直接导致发动机烧瓦抱轴。汽车发动机在线监测与故障诊断系统如能获取准确的油温信息,根据发动机的工况判断发动机的运行状态,对于确保汽车使用过程中的安全性具有重要意义。 为了检验分数阶积分算子对发动机远程检测信息数的的融合效果,选用安徽建筑大学建筑机械故障诊断与预警技术省级重点实验室的实验设备搭建实验平台,为了确保发动机正常运行时油温的稳定性,实验将发动机放置于有空调的实验室中,应用S-30铠装热电偶感知测量发动机在转速为2 500 r/min时运行30 min后的机油温度,并通过WiFi无线网络传送给信息采集系统。信息采集系统在较短时间内完成在室内、距离50、100、150、200、250、300、350、400 m的不同位置对发动机机油温度的实时采集工作,室内测量时油温值为测量真值85.04 ℃,室外远程检测时的测量数据如表1所示。 从表1所示的测量值可以计算出室外远程测量的油温平均值为83.446 ℃,与测量真值间的误差高达1.594 ℃,而且随着检测距离的增长,检测值与测量真值间的误差呈增大趋势,检测距离在400 m时,测量误差竟高达3.48%,显然超出了检测系统允许的误差范围。从实验环境可以看出,发动机油温数据的采集过程中,设备和检测仪器没有发生变化,因此以上检测误差的差异性应该来自于测量时间和地点的变动,但发动机处于有空调的实验室内,而且在测量过程中工况并未发生变化,故以上测量误差的差异性主要来自于检测地点的变化。信号采集系统位于不同的地点,测量时与信号源间的距离不同带来信号传输的能量损失存在差异,不同地点工作环境(如噪声、温度和湿度等)的不同也会带来检测数据间的差异性。 参照表1中所示检测数据,绘制图3所示的检测数据分布。从图3可以看出,发动机的油温测量值随着检测距离的增大呈下降趋势,但在多种因素的作用下,曲线并未呈现信号无线传输过程中能量衰减与距离的平方成正比的基本法则,而是一条检测数据离散分布的无规律曲线,检测数据间的方差(σ2)高达1.155,表明检测数据间波动过大,无法为汽车发动机在线监测与故障诊断系统提供可靠的油温检测数据,直接影响着系统工作的可靠性。 表1 实验数据 图3 检测数据分布曲线 3.3.1 检测值影响因子的选择 从实验环境的设置可知,表1所示数据是同一检测设备在不同位置对发动机油温远程检测的结果,检测数据间的差异性主要来自检测位置的不同。从图3可以看出,尽管检测数据呈现离散分布状态,但测量值与检测距离间的关系近似于一条二次函数曲线,故可以推导出:在发动机油温的在线远程测量中,发动机与数据采集系统的间距依然是影响测量值的主要因素。故案例采用发动机与信息采集系统间的距离作为发动机油温检测值的影响因子,探索应用检测距离作为外在影响因子x,分数阶积分算子对发动机远程检测数据的融合处理效果。 3.3.2 检测值与影响因子间关系式的拟合 参照已知点参数值{xi,yi}(1≤i≤n)拟合函数y(x)关系式的方法有很多,其中最小二乘法具有数据处理过程中不需数据先验信息的优点,可以通过寻求误差平方和最小化的方法拟合数据xi与yi(1≤i≤n)间的最佳函数式y(x),并可应用得到的函数式y(x)计算一些未知的数据,因在函数式的拟合中具有理想的拟合精度,最小二乘法而被广泛地应用于工程实践中。故本案例采用最小二乘法拟合数据采集系统在不同位置对发动机油温的测量值Ei及其与影响因子xi(测量距离)之间的函数式E(x)。根据理想状态下信号无线传输过程中能量损失与传输距离成正比的基本法则,可知E(x)应为二元二次函数,令函数式的各项系数为a0、a1、a3,E(x)表达式为 E(x)=a0x2+a1x+a2 (12) 参照表1中所示实验数据,应用MATLAB软件中Polyfit函数可拟合出式(12)中各项系数,可得相应的多项式方程为 E(x)=-1.809 5x2-8.333 3x+85.433 9 (13) 3.3.3 基于分数阶积分的检测数据融合模型 物联网下汽车发动机远程检测信息的数据融合算法模型如式(10)所示,从式(10)的组成可以看出,具体数学计算模型公式的获取,关键在于积分阶次(w)和步长(h)参数值的选择。 (1)阶次w的选择。从图1所示的分数阶积分算子幅频特性可以看出:在低频部分(0<ω<1),分数阶积分算子具有增强信息强度的作用,而且增强效果随着阶次w的增大而愈加明显;在高频部分(ω>1),尽管分数阶积分算子具有削弱信息强度的不足,但削弱程度也是随着阶次w的增大而有所减轻。为了节约篇幅,案例将分数阶次w取[0,1]的中间值0.5,探讨分数阶积分算子对检测数据的融合处理效果。 (2)步长(h)的取值。根据分数阶微积分的 Grunwald-Letnikov定义,可知步长(h)取值越小,则随着步数(n)的增多分数阶微积分的计算结果越精确,但步数(n)增多的同时也带来了计算工作量急剧增加的不足。案例综合考虑计算的精度和速度两方面因素,根据数据影响因子x(信号的远程传输距离)的取值范围为[0.05,0.4],按照式(10)中h→0的要求将步长h=0.01,这样需要计算的步数n=35,可以同时满足计算精度和速度两方面的要求。 现将分数阶次w=0.5和步长h=10代入式(10),可得案例中检测数据的融合算法模型为 0.5E(x-0.01)+ (14) 图4 0.5阶积分算子融合后检测数据分布曲线 (1)削弱信号强度的特性。根据表2中所示数据,可知经0.5阶分数积分算子融合处理后,发动机远程检测数据融合结果的平均值为55.118,与融合处理前检测数据的平均值为83.446相比,信号的强度下降了近34%。根据图1所示的分数阶积分算子幅频特性曲线,可知当分数阶次w和采样频率ω一定时,信号的增强(削弱)系数k为定值。故在本案例中,当参数w=0.5,h=0.01和n=35时,信号的削弱系数k=0.66,为了保证信号远程传输的可靠性和检测的准确性,可在信号传送前需对信号进行放大处理,放大系数Q=1.515。 表2 各检测点测量数据的0.5阶积分融合值 (2)有效融合去其他因素对测量值影响的特性。从图4可以看出,经分数阶积分算子融合处理后,检测数据间的波动比较小。图4所示数据分布曲线近视为一条直线,说明此时分数阶积分算子具有有效融合去信号在远程传送过程中其他外在因素(如工作环境的温度、湿度和噪声干扰)对检测数值影响的特性。 (3)远程获取高精度发动机运行信息测量值的功能。发动机远程检测数据经分数阶积分融合处理后,具有削弱检测信号强度的不足和有效融合去其他因素对测量值影响的优点。这样就可以先将表4所示的融合结果放大1.515倍,以修正经0.5阶积分算子削弱信号强度的不足,再根据信号无线传输过程中能量衰减与距离的平方成正比的基本法则,应用最小二乘法拟合出经分数阶积分算子融合处理后,油温检测数据与检测距离之间的二次函数关系式为 E′(x)=0.207x2-8.489x+85.345 (15) 应用式(15)可以计算出发动机近距离测量时(即x=0)的油温值应该为85.345 ℃,与实验中的测量真值间误差只有0.36%,大幅小于平均值法的1.9%和最小二乘法的3.1%。可见,分数阶积分算子具有远程获取高精度发动机运行信息测量值的功。 汽车发动机在线监测与故障诊断系统实现的技术难题在于:如何有效消除检测信息远程采集过程中各类影响因素对检测信号干扰带来的测量误差。通过对分数阶积分算子应用特性的研究,建立了基于分数阶积分算子的物联网下发动机远程检测数据融合处理模型,并通过0.5阶积分算子在发动机油温的远程检测系统中的应用,得出以下结论。 (1)分数阶积分算子具有削弱检测信号强度的不足和有效融合去其他因素对测量值影响的优点。 (2)在汽车发动机在线检测与故障诊断系统设计中,可以通过补偿分数阶积分算子在检测信号处理中削弱检测信号强度的不足。 (3)应用分数阶积分算子远程获取高精度的发动机检测信息数据,对于提高汽车发动机在线监测与故障诊断系统的工作准确性和决策科学性具有重要的应用价值。
2 基于分数阶积分算子的发动机检测信息融合处理技术
2.1 信息数据融合处理模型
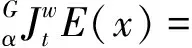



2.2 检测信息融合处理过程

3 分数阶微分算子在发动机油温远程检测数据融合中的应用
3.1 实验环境
3.2 数据分析

3.3 数据融合处理过程

3.4 检测数据融合结果及其分析处理



4 结论
