钢筋混凝土板柱节点受冲切承载力计算方法分析*

2021-02-23史庆轩蒋明月

建筑结构 2021年2期

史庆轩，蒋明月

(1 西部绿色建筑国家重点实验室/西安建筑科技大学，西安 710055;2 西安建筑科技大学土木工程学院，西安 710055; 3 西安建筑科技大学结构工程与抗震教育部重点实验室，西安 710055)

0 引言

板柱结构中板为无梁楼盖，可有效提高楼层净高，降低建造成本，多用于多层住宅、宾馆、医院、办公楼、停车场等。近年，此种结构类型在我国多发生整体坍塌事故，板柱节点处有明显的脆性冲切破坏，延性较差。因此，对其冲切机理及承载力计算方法进行分析具有重要的意义。

板柱节点的冲切失效模式分为三种：第一种为直冲破坏，白生翔[1]认为当板本身具有足够的刚度和整体承载力时，板会出现双向沿正截面剪坏，直冲柱体；第二种为冲切破坏，也称为双向剪切破坏，现在大部分理论认为冲切破坏是指两个方向的斜截面形成一个截头锥体，锥体斜截面大体呈45°倾角，破坏时钢筋可能未屈服，板面形成环状裂缝，其破坏形态类似于梁的斜拉破坏；第三种为弯冲破坏，破坏时板面已有较大的弯曲变形，柱周附近板内受拉钢筋屈服，然后受拉面出现以柱为中心的较大环状裂缝。需要特别说明的是，有学者[2]认为板的冲切破坏是弯曲和冲切共存的破坏形式。在板斜锥体冲出的过程中，斜锥面抗冲切力只是板发生冲切破坏时极限承载力的组成部分，而抵抗弯矩的能力在其形成弯曲破坏机构之前是始终存在的。

自20世纪60年代以来，结构工程师为研究板的抗冲切性能进行了大量的试验研究及理论分析，吴越凡等[3]综述评析了钢筋混凝土结构抗震性能，王璐等[4]对板柱结构体系及板柱节点的新进展进行了总结，但对受冲切承载力计算方法的介绍较少。目前，关于板柱节点受冲切承载力的评价尚未有定论，其中，根据我国《混凝土结构设计规范》(GB 50010—2010)[5](简称GB 50010—2010)计算所得的板柱节点受冲切承载力与实际都有一定偏差。

本文将介绍国内外学者根据不同理论背景推导出的板柱节点受冲切承载力的计算方法，分析混凝土强度、配筋率、截面有效高度、柱边长、纵筋屈服强度等主要因素对板柱节点受冲切承载力的影响，将其与以往试验数据进行对比。

1 板柱节点受冲切承载力模型理论

1.1 偏心剪应力模型

偏心剪应力模型是指板柱节点在受重力荷载及不平衡弯矩共同作用下，当临界截面上的剪应力达到临界应力时，板柱节点破坏失效。其中，板柱节点处的不平衡弯矩由板的弯矩和连接处产生的偏心剪应力传递的弯矩组成。临界截面上的剪应力为由不平衡弯矩引起的剪应力和同一截面处剪力引起的剪应力之和，且呈线性分布，见图1。

图1 偏心剪应力模型

1961年，Moe[6]将不平衡弯矩通过固定系数进行了分配，给出板柱节点抗弯和抗扭分配值，改善了原有偏心剪应力模型的适用性。1972年，Long[7]利用薄板理论进一步推进了偏心剪应力模型的计算方法，并给出4种破坏模式下的计算式及推导过程。我国规范GB 50010—2010和美国规范ACI 318-14[8]都以偏心剪应力模型为理论基础，此模型是板柱节点受冲切承载力计算模型理论的开端。

1.2 扇形模型

1960年Kinnunen和Nylander[9]开始对混凝土板抗冲切性能进行研究，估算了板的冲剪强度并给出板的极限转角ψ值的计算式。通过简化板的力学模型，并假定动量-曲率关系为双线性，计算出板的旋转能力，提出了对称旋转扇形模型。到目前为止，扇形模型仍然是考虑板柱节点发生冲切破坏的最佳模型之一，为后人进行板柱节点研究奠定了理论基础，但缺点是此模型计算过程复杂、应用困难。

随后，Broms[10-11]对Kinnunen和Nylander[9]的扇形模型进行了改进，并考虑了尺寸效应的影响，得到了板极限转角的解。瑞士的Robert Koppitz[12]等仍在Kinnunen和Nylander[9]对称旋转扇形模型的基础上，推导了考虑剪切对板弯曲行为影响的修正扇形模型，得到了在力学上更合理的抗弯刚度折减系数。

1.3 桁架模型

桁架模型是由混凝土压杆和钢筋拉杆组成的三维空间模型，借鉴了混凝土的拉压杆理论。受拉钢筋和混凝土受压区被分解成独立的杆系单元，其中压杆分为两类：一类平行于板平面(锚固压杆)；另一类与板的平面成α夹角(抗剪压杆)。每一个锚固压杆与相互垂直的钢筋平衡，因此，在距柱一定范围内的板内受拉钢筋都可以参与抗弯。

Van[13]首次利用混凝土的拉压杆理论描述板柱节点处荷载的传递路径，其中，混凝土压杆的状况与观察到的裂缝形态吻合较好平衡。缺点是所提出的拉压杆模型只适用于较小弯剪比的情况，横向剪力依赖于钢筋提供。

1987年，Alexander和Simmonds[14]提出了桁架模型，并将此模型应用在重力荷载和不平衡弯矩共同作用下的板受冲切承载力计算中。作者认为冲切破坏可分为四个阶段：1)柱附近的板受拉区形成弯剪裂缝；2)板内受拉钢筋屈服；3)弯剪裂缝延伸到混凝土受压区；4)受压区混凝土屈服失效。冲切破坏又可分为拉杆破坏和压杆破坏。另外，还有一种可能的破坏形式是压杆连接处产生平面外力，而此处没有外部荷载能与之平衡，从而超过板的极限承载力导致破坏。

1.4 断裂力学模型

断裂力学模型是混凝土模型中分析脆性材料中裂纹发展规律的模型。由于板在受冲切破坏过程中会形成大量裂纹，根据裂纹发展位置与状况可判断板的实际受力状况，因此断裂力学模型在分析板冲切破坏机理中有较好前景。1987年，Bazant和Cao[15]将断裂力学模型引入研究板冲切破坏过程。作者认为板的冲切破坏是随着裂缝尖端逐渐发展深入到结构内部的，不一定与冲切破坏面的形成同时进行。与其他理论模型相比，断裂力学模型中尺寸效应对板柱节点受冲切承载力影响尤其明显。

1996年，Hallgren等[16]对高强混凝土板柱节点试件进行了试验，基于非线性断裂力学理论，并利用混凝土受压区高度来推导尺寸效应对板柱节点受冲切承载力的影响。

1.5 临界剪切裂缝理论

2008年，Muttoni[17]提出了临界剪切裂缝理论。此理论假定临界剪切裂缝的宽度与板的旋转能力(斜率)成正比，其冲切强度受斜压杆剪力作用下产生的斜剪裂纹宽度与骨料粗糙度控制。此理论充分考虑了弯曲变形对板柱节点冲切破坏的影响。

临界剪切裂缝理论是在扇形模型的基础上发展形成的。在双向板中，临界剪切裂缝宽度wc与板的极限转角ψ和板的有效高度d成正比，即：

wc∝ψ·d

(1)

板柱节点在受竖向力作用时，剪力和弯矩复合作用引起的板内主拉应力的方向是倾斜的，当主拉应力超过混凝土的抗拉强度时，将出现斜裂缝。通过计算每一条弯剪裂缝对应的破坏准则曲线与力-转角曲线的交点可获得每一条裂缝对应的冲切荷载及板端的冲切转角，将冲切荷载作用下最小的裂缝视为临界裂缝，相应的冲切荷载即为板柱节点最终的冲切荷载。如图2所示A点即为构件的冲切破坏点。因此，依据临界剪切裂缝理论计算板柱节点受冲切承载力，需求解两条曲线。

图2 破坏准则曲线和力-转角曲线

2009年，Guandalini等[18]根据临界裂缝及其抗剪能力，通过骨料尺寸(dg0+dg)(dg0为参考尺寸，一般设定为16mm；dg为最大骨料尺寸)对裂缝宽度进行细分，对原有的破坏准则进行了修正。

2018年，王志军[19]等在临界剪切裂缝理论的基础上，针对第一条弯曲裂缝起点位置的确定和钢筋的销栓作用两个问题，对临界剪切裂缝理论进行了修正，提出了配有抗冲切钢筋的板柱节点临界剪切裂缝计算方法。

1.6 塑性理论

李政启等[25]基于抛物线形Mohr-Coulomb准则，并考虑到板冲切裂缝开展到抗弯钢筋处，抗弯钢筋因斜裂缝两边有相对的上下错动而受到一定的剪力，延缓混凝土裂缝的开展，提出了考虑抗弯钢筋销栓作用的钢筋混凝土板受冲切承载力计算式。利用Mohr-Coulomb进行抗冲切塑性分析时，此准则中的包络线相切于单轴抗拉和单轴抗压莫尔圆，如图3所示。其中抗弯钢筋的销栓作用约占钢筋混凝土板受冲切承载力的6%～11%，从而认为，忽略抗弯钢筋的销栓作用是相对不合理的。其中，考虑抗弯钢筋的销栓作用的计算式如下：

图3 Mohr-Coulomb准则

(2)

式中：Pb为抗弯钢筋的销栓作用所提供的受冲切承载力；∑Rb2为与破坏锥面相交的各方向上所有抗弯钢筋直径的平方和;fy为抗弯钢筋屈服强度;ζ为抗弯钢筋拉应力与其屈服强度的比值，ζ取0.8；α为包络线外法线方向与τnt轴方向的夹角，取64°。

易伟建等[26]基于抛物线形的Mohr-Coulomb准则，推导出了求解混凝土板柱节点受冲切承载力最小上限解的偏微分方程，分析出方柱、圆柱节点冲切破坏屈服面上的空间应力分布状况，发现圆柱和方柱节点柱边的应力高于板底的应力，方柱节点在柱角处存在应力集中现象。2017年，易伟建等[27]在塑性理论基础上提出钢筋混凝土板冲切开裂滑移模型，即斜截面在形成塑性屈服面的同时开裂发生滑移引起节点冲切破坏。此模型解释了板柱节点在集中力作用下冲切锥面的角度大于均布荷载作用下冲切锥面的角度的现象。

严宗达[28]采用双剪强度理论对混凝土板轴对称受冲切承载力进行了计算，并利用虚功方程求得破坏荷载的上限解。蔡健等[29]在此基础上将混凝土板的冲切破坏简化为平面应变问题，利用双剪应力三参数强度准则对发生冲切破坏的混凝土板剪压区的复合应力进行分析，指出板的冲切破坏与梁的剪切破坏都是由于剪压区混凝土在复合应力下发生脆性破坏所导致的，但梁的剪切破坏可简化为平面应力问题，板发生冲切破坏时空间作用显著，可近似于平面应变问题。

1.7 切向应变理论

切向应变理论以结构力学和混凝土本构关系为基础，与桁架理论有相似之处。2016年，Broms[30]提出了一种新型无抗冲切钢筋板发生冲切破坏的力学模型，既能预测板柱节点的抗冲切能力，又可以计算板的极限旋角，同时适用于偏心冲切问题。

切向应变理论是假设剪力通过斜压杆传递到柱上，见图4，挤压到柱附近的板混凝土压缩区。由此产生的挤压力可分解为径向拉应力和切向压应力。随着荷载不断增加，当切向压应力达到屈服时，不断增加的径向拉应力使得附近的混凝土被锚固。当产生的拉应力超过由于弯矩引起的径向拉应力时，在柱周围会有拉伸裂缝，该裂缝即为引起冲切破坏的原因。简言之，板柱节点的冲切破坏是由斜压杆的水平分量引起的，该破坏过程可表示为受弯矩作用下关于柱边混凝土应力-应变的函数。

图4 切向应变理论荷载传递路径

切向应变理论是依据切向压缩应变值来判断板的受力情况的。当边缘切向压缩应变到达临界值εcpu时，荷载将达到极限应力。由于柱边的总压应力将达到普通强度混凝土的屈服应力，因此在柱弯矩作用下，设切向压应变达到1.0‰时，板柱节点将达到冲切极限荷载。若混凝土强度较高、脆性较大，可以进一步假定临界应变值随混凝土强度的增加而减小。切向应变理论考虑了混凝土的尺寸效应，并通过破坏准则反映混凝土脆性变化程度。

1.8 临界截面应变理论

2010年，Park等[31]提出了临界截面应变理论，其冲切强度是由剪切能力曲线与需求曲线交点位置确定的，此处与临界剪切裂缝理论相似；同时，作者根据等代梁原理将板转换为两个正交方向的等效梁进行受力分析。为了将该临界截面应变理论应用于实际，建立了简化的强度模型，并引入了尺寸效应和非均匀剪应力分布两个修正因子。临界截面应变理论重点分析板柱节点弯曲裂缝，认为板柱节点在发生冲切破坏前已有弯曲开裂。临界区混凝土在压应力和剪应力共同作用下，发生压缩破碎或拉伸开裂而破坏。

Park等[31]还发现随着混凝土抗压强度的增大，混凝土抗拉强度也增大，板的冲切强度也随之增大。然而，由于混凝土的抗压强度过高，降低了受压区深度，因此冲切强度并不与混凝土强度成比例增加。另外，随着配筋率的增大，混凝土受压区高度增加，冲切强度随之增大，可知在一定范围内配筋率与冲切强度成正比例关系。

2 几种板受冲切承载力计算方法

各种模型的理论背景不尽相同，推导简化过程也有差异，得出了可用于实践的计算方法。本文选取几种较有代表性的板受冲切承载力计算方法，并与我国规范 GB 50010—2010进行比较，见表1。其中，临界剪切裂缝理论需求解二元一次方程组，相比于其他公式，运算相对复杂，给出的板达到受弯承载力极限值时对应的剪切力Vflex的计算式可有助于判断板的破坏形式。

各理论模型的受冲切承载力计算式表1

各公式考虑的影响因素表2

3 影响因素分析

将第2节所列5种板柱节点受冲切承载力计算式中的参数进行汇总，见表2。为体现各因素对板冲切荷载的影响程度，选取Elstner等[32]的一组试验数据“A-3c”(表3)，在其他参数不变的情况下，分析板有效高度、配筋率、柱边长、混凝土强度、钢筋屈服强度这些因素对节点受冲切承载力的影响。

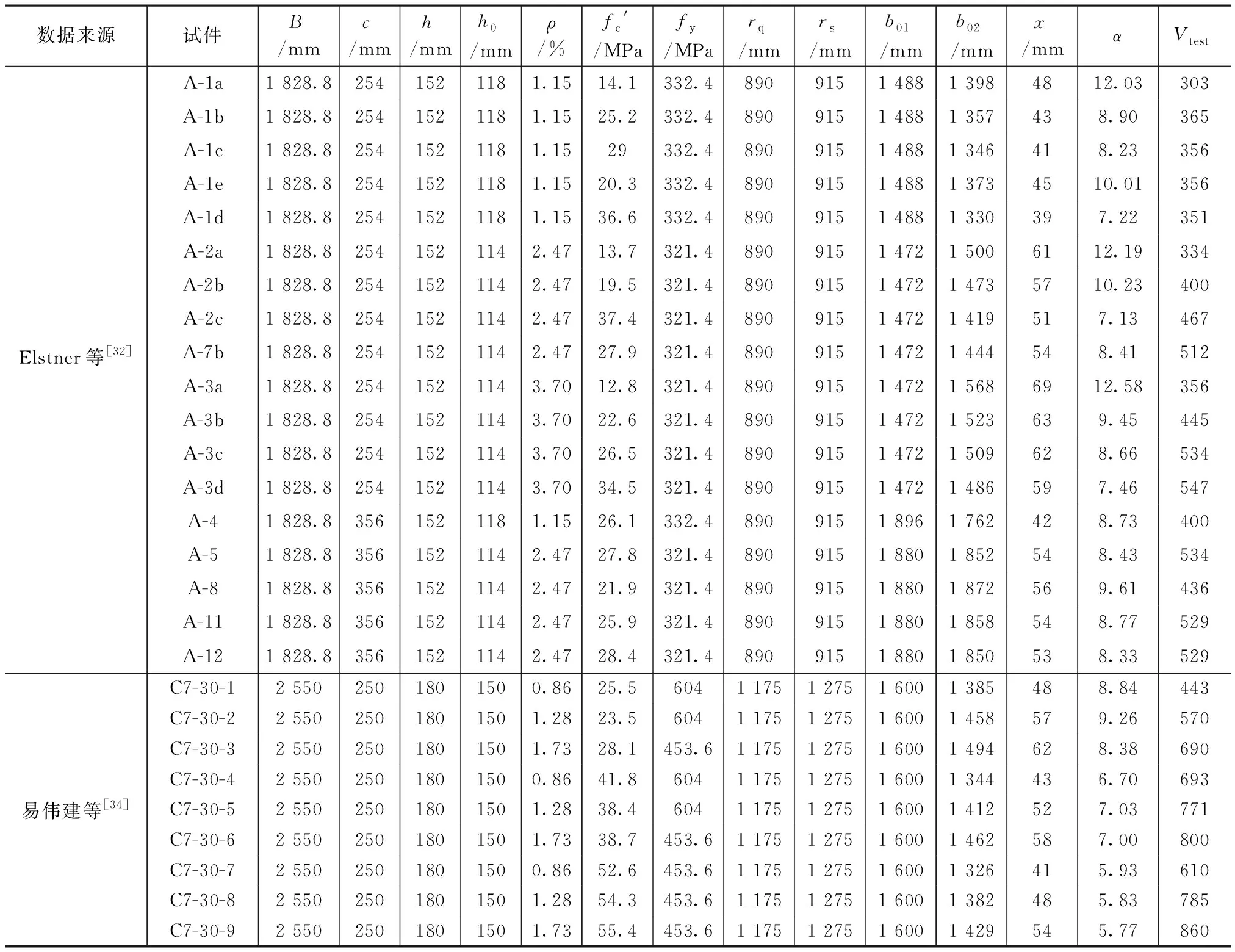
试验数据表3

3.1 混凝土强度

由图5(a)可知，混凝土强度对板受冲切承载力影响较大，且随着混凝土抗压强度的增加，5个计算式得出的结果都呈上升趋势。但由于板柱节点处的混凝土受力状态较为复杂，因此混凝土强度与受冲切承载力之间并不是简单线性关系。李定国等[33]认为板柱连接处破坏锥体成明显的撕裂状，采用混凝土的抗拉强度更切实际。由图5(a)还可知，V2有波动上升趋势，这是由于V2的计算式中根据混凝土强度等级设置不同的参数参与运算所导致的；临界截面应变理论的V5随混凝土强度增加变化幅度最为明显，与其他计算式结果相差较大。

3.2 板有效高度

在计算板柱节点受冲切承载力时，板有效高度相比板厚更具有代表性，与计算受弯构件斜截面受剪承载力类似，有效高度可反映参与受力的实际高度。单纯增加板厚并不能有效提高板抗冲切性能，且受实际工程限制。由图5(b)可知，板有效高度的变化对V2影响较小，因为V2的计算式中涉及板有效高度部分系数变化较小，无法体现其真实变化程度。

3.3 柱边长

板有效高度和柱尺寸都会影响其发生冲切破坏时的临界截面周长，板有效高度越高，且柱的边长越长，则临界截面周长越大。其中，临界剪切裂缝理论的V1计算式中虽然没有单独出现此参数(临界截面周长)，但考虑了临界截面周长，使得V1在图5(c)中的变化最不明显。

3.4 配筋率

提高板的配筋率可有效提高其受冲切承载力，抗拉钢筋能抑制斜裂缝的开展和延伸，且纵筋数量增加，其销栓作用也随之增加。如图5(d)所示，除V2外，V1,V3～V5的上升趋势相似，当配筋率小于1%时，受冲切承载力上升较快，配筋率大于1%时，V3持续增长，与其他理论推导数值相差越来越大，说明V3的计算式放大了配筋率对于提高板受冲切承载力的作用。

图5 各影响因素对板柱节点冲切承载力的影响

3.5 钢筋屈服强度

众多试验结果表明，钢筋屈服强度会影响板柱节点的受冲切承载力，但由于发生冲切破坏时，受拉钢筋一般未屈服，所以与其他影响因素相比，提高钢筋屈服强度对改善板抗冲切性能的影响较小，由临界剪切裂缝理论计算的V1甚至出现了下降的趋势，因此将钢筋屈服强度与配筋率共同考虑会更加合理。

4 受冲切承载力计算分析

为分析各参数对板柱节点受冲切承载力的影响，本文选取27个试件进行对比，试件数据来自于Elstner等[32]和易伟建等[34]进行的板柱节点试验的部分数据，见表3。采用表1中5个理论公式和规范GB 50010—2010的公式对这些试件的受冲切承载力进行计算，计算结果见图6。

由图6可知，由临界剪切裂缝理论计算的V1与试验的Vtext很接近，且标准差较小，与实际有较好吻合。由塑性理论推导的两个公式(即表1中塑性理论的两个公式)计算的V2和V3普遍大于试验的Vtext，说明利用塑性理论在公式推导过程中，忽略了一些重要影响因素，例如板边长B等，导致过高估计了板柱节点的受冲切承载力，在实际中不建议采用，存在一定安全隐患。如图6(e)所示，虽然试验的Vtext与临界截面应变理论计算出的V5的比值的散点分布分散，但计算的V5整体接近于试验的Vtext，表明，V5公式对某些情况可以做出较好预测，同时也说明塑性理论不具有稳定性。根据规范GB 50010—2010计算出的受冲切承载力VGB远远小于试验的Vtext，证明规范GB 50010—2010的受冲切承载力公式有大量的安全储备，与实际情况相差较大。对比这6种板柱节点受冲切承载力计算方法，临界剪切裂缝理论与实际冲切情况最为接近，准确性更好，更具参考价值。