含谐振单元和弹性支承谐振单元的声子晶体低频禁带特性研究

2021-02-23王红赛

人工晶体学报 2021年1期

李竞,王红赛,关栋,张纯,沈辉

(扬州大学机械工程学院，扬州 225127)

0 引言

随着现代科学技术水平的飞速发展，人民生活水平的快速提高，车辆、船舶、飞行器等运载工具以及家电设备等成为人们生活中不可或缺的部分。然而这些设备在运转过程中会产生令人不悦的振动，特别是低频振动。如何抑制低频振动是振动噪声控制领域的重要问题[1-4]。声子晶体[5]的提出，特别是局域共振禁带机理[6]的提出，为低频振动控制提供了重要理论支持[7-9]。

在对声子晶体的研究中，弹簧质量链模型因其结构简单、力学模型清晰而受到学者的青睐。早在2003年，Jensen[10]通过弹簧质量链模型研究了材料属性周期分布的一维和二维结构。此外，对局域共振声子晶体的研究表明，其共振模式与多自由度系统的共振模式具有相似性[11]。因此，能够将连续体模型简化为弹簧质量链模型，进而探索其低频段的动力学特性。通过这种简化方式，学者们分别研究了含有单个共振子[12-13]、含有多个共振子[14-15]、含有不同阻尼模型[16-17]、含有弹性支承边界条件[18-19]的弹簧质量链模型。研究表明，此类结构存在禁带，且禁带内结构的动态等效质量为负数[13-15]。此外，Liu等[20]还对结构的动态等效刚度进行了求解，他们发现在某些禁带内动态等效刚度也存在负值。在上述结构中，含弹性支承的声子晶体因其第一禁带从0 Hz开始而受到学者关注[21-25]。Lee等[21]在研究一种具有骨架的一维薄膜阵列结构时发现该结构在0～735 Hz间具有强烈的声衰减作用。事实上，含弹性支承的弹簧质量链模型即是这种具有骨架的薄膜结构的理论模型[18,22]。Li等[23]通过对这种含弹性支承的声子晶体进行设计，得到了一种声二极管。Liu等[24]将这种含弹性支承结构的设计思想扩展到高维结构，并得到了具有低频禁带的二维结构。随后，Liu等[25]设计了一种复合杆结构，通过将硬质外壳夹紧固定模拟固定约束，从而实现周期弹性支承结构，用实验验证了这种含弹性支承的声子晶体的动力学特性。

本文提出了一种具有谐振单元和弹性支承谐振单元的声子晶体结构。通过声子晶体理论、等效介质理论和振动理论，计算了该声子晶体结构的能带关系和有限结构的振动传递曲线，并考察该结构的禁带调控特性。研究表明，该结构第一禁带的起始频率为0 Hz，禁带对弹性波衰减强度由有限结构周期数和衰减因子共同决定，谐振单元和弹性支承谐振单元的结构参数对低频禁带的频率范围具有重要影响。

1 理论模型

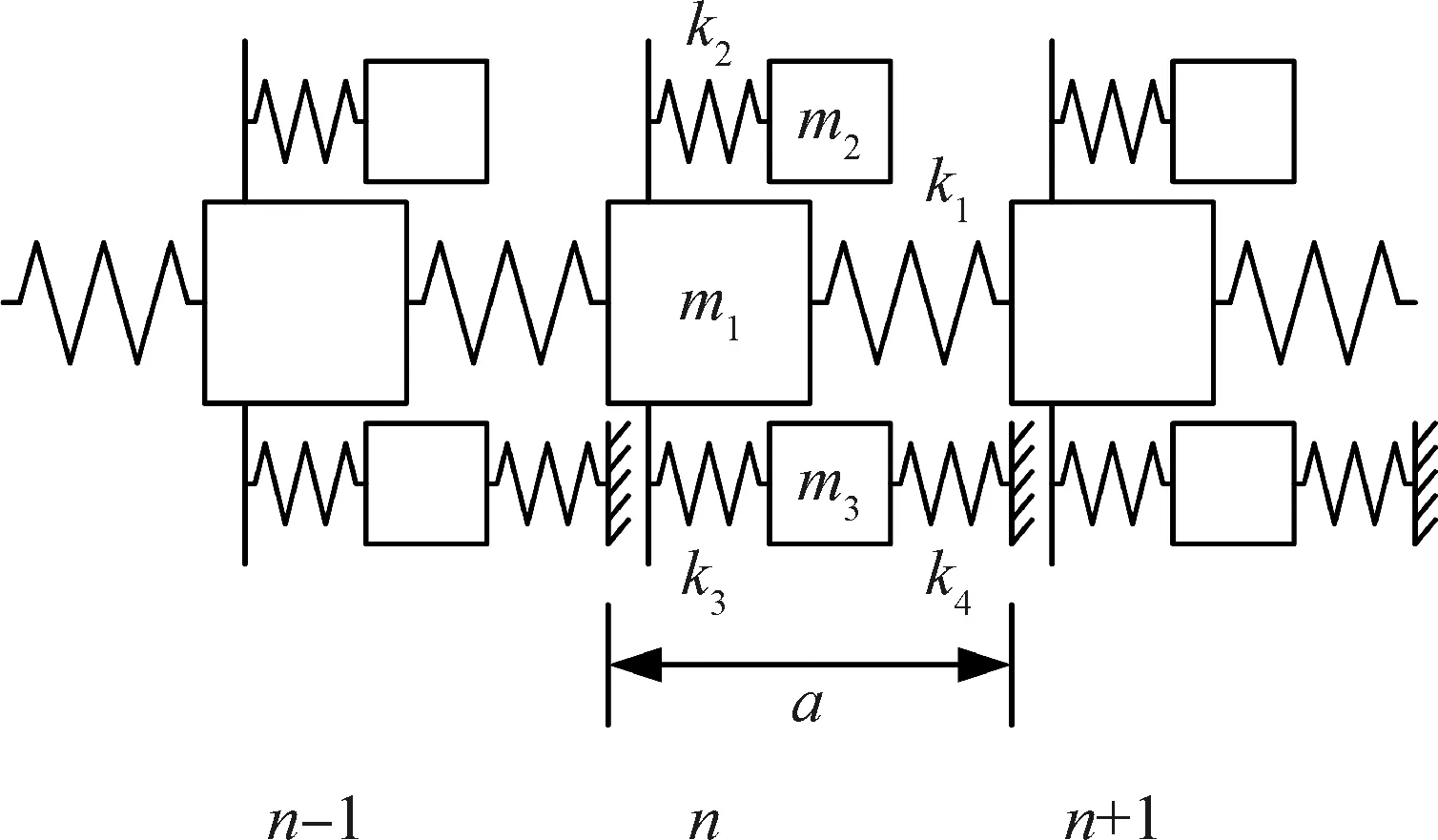
图1 具有谐振单元和弹性支承声子晶体的结构模型图

具有谐振单元和弹性支承谐振单元声子晶体的结构模型如图1所示。该结构由一条左右无限拓延的弹簧质量链以及从属于该弹簧质量链的谐振单元和弹性支承谐振单元构成。弹簧质量链中质点的质量为m1，弹簧的刚度为k1，不同质点的间距均为a；谐振单元中质点的质量为m2，弹簧的刚度为k2；弹性支承谐振单元中质点的刚度为m3，弹簧的刚度分别为k3和k4，其中刚度为k3的弹簧将m3和m1相连，刚度为k4的弹簧则将m3与固定约束相连。

当弹性波在该结构中传播时，对于第n个单元有动力学方程组：

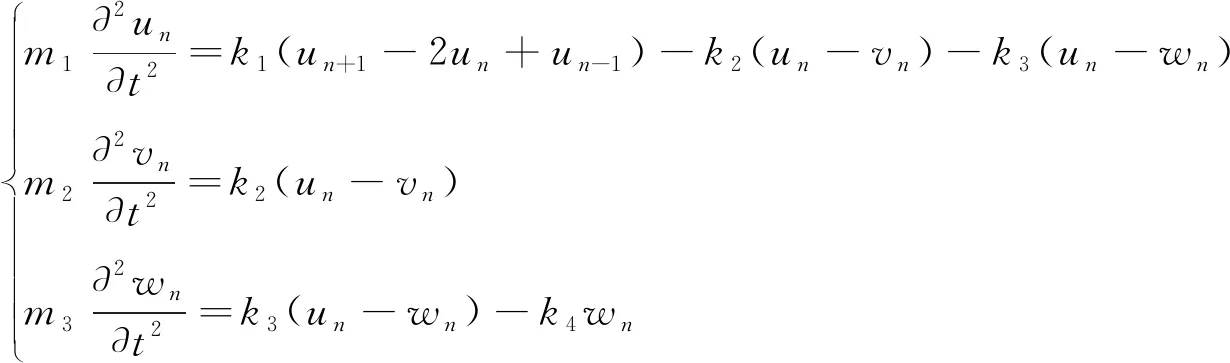
(1)

式中，t表示时间，un、vn和wn分别表示第n个原胞中质点m1、m2和m3的位移。在稳态条件下，式(1)的解可以写为：

(2)

式中，x表示质点所在位置，U、V和W分别表示结构中三类质点的位移幅值，q为弹性波的波数，ω为弹性波的角频率。将式(2)带入式(1)并写成矩阵形式有：

(3)

若要式(3)有解，则其中行列式的值为零，进一步可得到该结构的色散方程，即

(4)

其中：

(5)

观察式(4)不难发现两种计算结构色散曲线的方法。第一种方法是给定归一化波矢qa求解角频率ω，这将得到一个关于角频率ω的六阶多项式方程。求解该方程将得到三组互为相反数的解，舍去复数解后，得到本结构的三条色散曲线。第二种方法是给定角频率ω求解归一化波矢qa，这将得到一个关于归一化波矢qa的三角函数方程。求解该方程得到的归一化波矢qa具有复数形式，即qa=α+iβ，其中β表示衰减因子。衰减因子的出现在无限周期结构中表现为弹性波带隙，在有限周期结构中表现为弹性波衰减。因此，本文采用第二种计算方法计算结构的色散曲线。

为了验证复能带计算的正确性及衰减因子对传输特性的影响规律，本文进一步计算了具有弹性支承和谐振单元声子晶体的弹性波传输特性。首先对结构进行均质化等效，即将谐振单元和弹性支承谐振单元并入假想的等效质量meff中，如图2(a)所示。

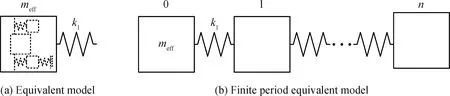
图2 具有弹性支承和谐振单元声子晶体的等效结构模型图

通过采用前文的理论分析方法，能够得到图2(a)中弹簧质量系统的色散方程，即

(6)

对比式(4)和式(6)不难发现，若要等效模型与具有动态质量的弹簧质量链模型具有相同的色散关系，则必有

(7)

进一步建立有限周期的等效结构模型，如图2(b)所示。对该结构进行动力学分析有

(8)

式中，Uj表示第j个质点的位移幅值。令相邻两质点的弹性波传递率为

(9)

将式(8)带入式(9)有

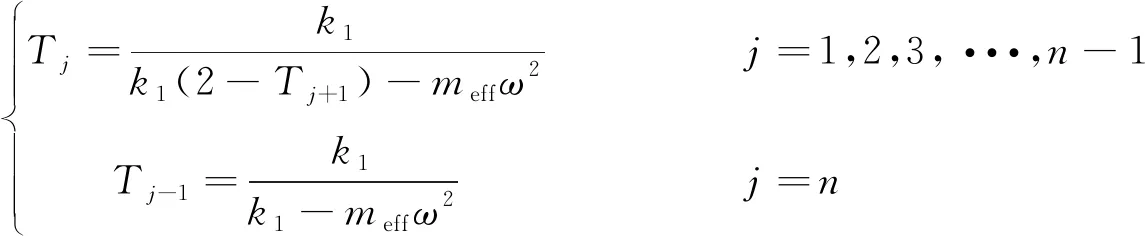
(10)

整体结构的总传递率有

(11)

分别将相关参数带入式(4)和式(11)计算，即可得到具有弹性支承和谐振单元声子晶体的复能带结构图和有限结构的弹性波传输特性曲线。

2 结果与讨论

图3即为计算所得的谐振单元和具有弹性支承谐振单元声子晶体的复能带结构图和有限结构的弹性波传输特性曲线。从图3(a)中可以看出，在不同角频率ω的取值下，归一化波矢qa的取值可以分为两类：第一类是实部在0到π间取值，且虚部为0，此时角频率ω落在结构的通带内；第二类是虚部不为0，此时角频率ω落在结构的禁带内。即当衰减因子为0时，结构存在通带；当衰减因子不为0时，结构产生禁带。观察图3(a)可以发现，该结构在角频率为0～3的范围内存在四个弹性波禁带，这四个禁带的角频率范围分别为0～0.44，0.88～1.25，1.35～1.80和2.53～3，即图中显示的四条禁带的禁带宽度相差不大。观察禁带内衰减因子的变化规律可以发现，在第一禁带和第四禁带内，衰减因子在禁带边界处的变化速率较大，而在远离禁带边界的区域，变化速率较小；相反，在第二和第四禁带内，衰减因子的变化速率在禁带范围内均较大。图3(b)中原始模型曲线，即实线，表示元胞结构为图1的仿真计算结果；等效模型曲线，即圆圈符号，表示元胞结构为图2(a)的理论计算结果。对比两者可以发现，在不同周期数下等效结构曲线与原始结构曲线基本重合。这说明可以通过等效方法来计算有限结构的传输特性，因此，运用这种等效方法进行计算不但能极大地降低运算量，而且计算结果的准确性并不会降低。该图中曲线①与方形符号表示周期数为3的有限周期结构计算结果，曲线②和圆圈符号表示周期数为5的有限周期结构计算结果。从这些曲线与圆圈符号中不难看出，禁带范围内的传递率存在明显的衰减现象，且周期数越大，传递率的衰减量越大。此外，对比图3(a)和(b)不难发现，衰减因子越大，传递率衰减越强。周期数和衰减因子对传递率的影响亦可通过理论推导“近似”得到，即将式(2)和式(9)带入式(11)可得

(12)

观察式(12)不难发现，传递率T中分母e的指数为虚数单位i、周期数n以及归一化波矢qa的乘积。当归一化波矢qa为虚数，即衰减因子不为0时，总体的传递率T总小于1，并且衰减因子对传递率的影响规律与周期数对传递率的影响规律相同。因此，衰减因子越大，传递率的衰减越大。这里需要指出的是，由于式(2)是无限周期声子晶体结构的动力学解，因此由此计算得到的式(12)为无限周期声子晶体结构的振动传递率表达式。无限周期声子晶体结构的动力学方程与有限周期声子晶体结构的动力学方程仅在边界处略有不同，这种差异对禁带内的弹性波传播规律影响不大。因此可以通过式(12)近似地分析相关参数对有限结构中禁带内传递率的影响规律。

由于衰减因子对结构的动力学特性有着重要影响，因此有必要探索具有弹性支承和谐振单元声子晶体中相关参数变化对衰减因子的影响规律。首先对谐振单元和弹性支承谐振单元中的相关参数进行归一化处理，即将谐振单元中的质量m2和刚度k2以及弹性支承中的质量m3、刚度k3和刚度k4分别除以主链的质量m1和刚度k1，得到归一化质量Δm2和Δm3以及归一化刚度Δk2、Δk3和Δk4。随后将这些参数带入式(4)中求解衰减因子。图4显示了上述参数变化对衰减因子的影响规律。图中深蓝色区域①表示衰减因子为0，结构处于通带；浅蓝色区域②表示结构处于禁带，但衰减因子较小，减振效果一般；黄色区域③表示结构处于禁带，衰减因子较大，减振效果较好。从图4中不难看出，在大多数情况下，结构在0.1～10 Hz的范围内存在三条通带和四条禁带。其中第一条禁带和第四条禁带仅在归一化质量和刚度过大或者过小时才发生变化，剩余两条禁带中有一条禁带对归一化质量和刚度变化比较敏感，另一条则对归一化质量和刚度变化不敏感。因此可定义对归一化质量和刚度变化敏感的禁带为可调禁带，对归一化质量和刚度变化不敏感的禁带为不可调禁带。

图3 复能带结构图以及传输特性图

图4 支链中质量和刚度变化对衰减因子的影响规律

通过图4(a)可知，随着归一化质量Δm2的增加，可调禁带逐渐降低，随后与不可调禁带相交，并最终落在不可调禁带之下。同时，不可调禁带的范围随着归一化质量Δm2的增加而增加。通过图4(b)可知，随着归一化刚度Δk2的增加，可调禁带向高频段移动，随后与不可调禁带相交，并最终落在不可调禁带之上。同时，不可调禁带的减振效果随归一化刚度Δk2的增加而提高。这里需要指出的是，在1～10这一范围内调节归一化刚度Δk2不仅能够提升抑制高频段弹性波的能力，同时也能够利用通带特性对弹性波进行滤波。观察图4(c)不难看出，归一化质量Δm3对衰减因子的影响与归一化质量Δm2类似，均使可调禁带从高频段移动至低频段。对比图4(d)和(e)可以看出，随着归一化刚度Δk3或Δk4的增加，可调禁带从不可调禁带上分离后将继续向高频段移动。但是归一化刚度Δk3的增加对减振效果的提升要优于Δk4的增加。