关于弧度制中几点误读的分析

王姿婷 朱一心 王 安

(首都师范大学数学科学学院 100048)

1 问题提出

在小学及初中教材中,平面角的度量是先以角度制形式出现的,即将一个圆周角表示成360°.在此基础上展开了关于平面角的比较、平面几何图形的研究,并在含有特殊角的直角三角形中讨论三角函数.而高中教材中,任意角的三角函数则以弧度制的认识开始,即将一个圆周角表示成2π(rad).关于引入弧度制的必要性,有几种常见的说法:1.“借助单位圆建立角度与对应弧长的关系,用对应弧长刻画角的大小;因为长度单位与实数单位一致,这就使得三角函数的自变量与函数值的取值都是实数,符合对应关系的函数定义”;2.“角度作为自变量表示三角函数,还存在一个突出问题,就是自变量的值与函数值不能进行运算(例如, 60°与sin60°不能相加),阻碍了三角函数通过运算法则形成其他初等函数”;3.“(角度制中)自变量的取值是60进位制的角度,不是10进位制的实数,不符合对应关系的函数定义”[1,P.111].文献[9]主要针对上述第一个说法进行论述,本文增加了对后面几种说法的分析;与文献[10]相比,在实数的进位制表示与度量单位间进率的区别,以及自变量的值与函数值不能运算等问题有了更清晰的表述,同时更深入了物理量纲的讨论.

2 基本概念

2.1 数与量

在讨论度量制的内容之前,先对“数”和“量”的相关概念进行划分,以避免因语义不同带来的表达偏差.

数(作为名词),是人们从生产和生活实践中抽象出来的,如自然数、有理数、实数等.从现实世界中客观对象的多少开始,人们对数有了最原始的感受.一方面,数可以表达各种现实对象的数值特征,另一方面,数又是人类创造出的形式化表达,这种形式化的本质不依赖于现实对象的特殊属性,甚至不依赖于表达数的符号.

量(作为名词),泛指可以定性区别和定量确定的属性,如现实中的距离、面积、重量等.类似地,数学中的测度“作为线段的长度,平面图形的面积,空间图形的体积等概念的抽象与扩充”[2,P.841],也可以理解为“量”.

度量(作为动词),就是通过比较,对给定的量赋予数值(根据文献[3,P.7],这种赋值具有可列可加性)的过程(有时度量也作名词,指某种度量方法).在度量时,首先要选取一个与给定量同类的量作为标准,即作为单位(通常称为单位量,也称为度量单位),进而约定比较的方式,得到其定量指标——度量值(即数值(1)数值是物理对度量值的称呼,因度量值本质上是一个数,故数值一词的用法在数学和物理中无明显区别.).度量值一般赋值为给定量与单位量之间的比值(2)与拥有天然不可分割单位的量(例如一个人)相对的,有些量无法通过“数个数”来确定给定量与天然单位间的数量关系(例如线段长度),这类量可以无限细分,而度量则提供了处理这些量的办法,其无限细分的性质也成了其度量值(实数)连续性的直观对应.关于天然不可分割单位的量的简单描述,见项武义主编教材[17,P.12]..例如某人的身高h为1.7m,就是将人抽象成一条线段,它恰好是人为选取的长度单位1m的1.7倍.不同的度量标准和方法称为不同的度量制.“单位本身也是一个量(3)单位一般相当于“数值等于1的量”(也有某些约定作为单位的特定量其数值并非1).通常地,单位这个词也被用于特定度量制中单位量的名称符号,如1.7m中的m,但其本质与1m无异.……单位与量之间只有定性的关系,加上数以后才有定量的关系”[4.P10].一个量总是可以表达为量值的形式,即“数值与单位的积”[4.P3],如1.7m,就是度量值1.7与单位m的积.“当说明某物理量为多少时,必须同时说明单位,否则没有意义”[5,P.13].有时会有“面积为4”的数学结果,这种说法蕴含着“4平方单位”或者“面积的度量值为4”的简化,在解释物理现象时不能单独称“面积4”.

在物理层面,“由于量与量之间常常是相互联系的,因此没有必要对每个量的单位都逐一规定,只需选取基本的物理量作为基本量(4)基本量与单位量是有区别的,单位量是某类量在某种度量制中的标准,而基本量则是某一量制(物理名词)中选出的一组彼此相互独立的量,其它的量是由基本量以乘和除的代数关系导出的.国际单位制SI中,选择长度、质量、时间、热力学温度、电流、物质的量和发光强度这七个量作为基本量.,基本量的单位称为基本单位.由基本量导出的其他物理量称为导出量,导出量的单位称为导出单位.表示每个物理量如何由基本量组成的公式,称为该物理量的量纲公式,简称量纲”[6,P.88].通常将结合某些特定的物理定律及概念,对量之间的量纲关系作相关界定或分析的方法称为量纲分析.

2.2 角度制与弧度制

3 对引入弧度制的必要性相关观点的分析

3.1 “借助单位圆建立角度(7)严格讲这应该是平面角而不是角度,以免与角度制中的用词混淆.与对应弧长的关系,用对应弧长刻画角的大小(8)由弧度制定义,“弧长刻画角的大小”的说法易引起误解,见注③及下页注④.;因为长度单位与实数单位一致,这就使得三角函数的自变量与函数值的取值都是实数,符合对应关系的函数定义.”

一方面,“长度单位与实数单位一致”的说法混淆了不同类的单位量,长度单位是1m,1km等单位量,而实数单位是数值1,二者一致的说法无从谈起.诚然,线段通过度量可以对实数进行几何直观表征,但现代数学中实数系统的建立无需借助于线段或其他具象,若将实数与长度等同视之,实数系统中许多运算将变得无法解读,如开方、取对数等.就好比于将自然数停留在现实存在的物体个数层面上理解,那“1个对象×1个对象+1个对象”也是无法进行的.

另一方面,角度制和弧度制下定义的三角函数都是实数集到实数集的映射,具体分析如下：

角度制和弧度制虽采用了不同的单位量,但两种度量制下的度量值都是实数.例如1度和1弧度,单位量的不同不会引起这个“1”的实数属性发生变化.“这两种度量制,都能够实现在平面角的集合与实数集之间建立一一对应关系”[8,P.8].任意给定一个实数作为度量值,都能在相应的度量制下唯一决定一个平面角(例如在弧度制下,度量值2对应了2 rad的平面角,在角度制下度量值2则对应着2°的平面角),进而又能唯一决定其对应的三角函数值.

因此,基于两种度量制下定义的三角函数都是实数集到实数集的映射,不会因单位量的选取不同而造成差异.这在李忠《为什么要使用弧度制》[9]以及朱一心《弧度制教学中相关问题的问答》[10]中均有指出.

3.2 “角度作为自变量表示三角函数,还存在一个突出问题,就是自变量的值与函数值不能进行运算(例如, 60°与sin60°不能相加),阻碍了三角函数通过运算法则形成其他初等函数.”

下面分三点来阐述该表述涉及到的问题:

(1)弧度单位的省略

在平面角的两种度量制中,约定“用弧度制表示角(10)依原文,此处的角指的是平面角.时,‘弧度’二字或‘rad’通常略去不写,而只写该平面角所对应的弧度数”[7,P.174],即角度制下，一个量值必须带着“°”,在弧度制中,量值可略去单位“rad”.这种人为约定能带来书写和表达上的便利,但随之而来的问题是,它模糊了弧度制下量值与度量值(弧度数)的区别.

(2)平面角的量纲问题

平面角的单位弧度(rad)通常被约定略去不写,除了表达便利性外,还有量纲层面的考虑.

“在1960年的第11届国际计量大会(CGPM)将平面角的单位弧度(rad)和立体角的单位球面度(sr)规定为国际单位制的辅助单位,提出它们既可作基本单位使用,也可作导出单位使用,并认为平面角和立体角既可认为是基本量,也可认为是导出量……而1995年召开的第20届国际计量大会正式决定:在SI中称为弧度和球面度的这两个辅助单位是一种无量纲的导出单位,因而在SI的分类中应当取消辅助单位”[11,P.42].根据文献[4,P.74],度(°)是我国选定的SI制外单位(11)不属于SI的单位..

(3)数学与物理中的运算

数学上的运算是同类对象之间的二元映射,受到运算结构本身的性质约束,不涉及任何描述物理属性的单位,更不涉及量纲分析.事实上,数学抽象化的过程已经舍弃了具体的物理属性.

物理关系常常借用数学运算来表达,这具有显见的简约性和便利性,但它们需要满足物理的特定要求.例如量纲公式只表达一个定性关系而非定量关系、等号两端各代数项的量纲必须相同、只有同类量才可以相加或相减等.

数学提供的是运算的合理性,被运用到单位或者量纲上,是出于物理方程经由数学运算的结果需要解释自洽的考虑.注意到这点,才不会混淆数学运算和物理讨论两方面的归因.

不难发现,“角度作为自变量表示三角函数,还存在一个突出问题,就是自变量的值与函数值不能进行运算(例如,60°与sin60°不能相加),阻碍了三角函数通过运算法则形成其他初等函数”是用无因果关系的名词堆砌的伪问题.本质上是因为将直观表征的量与数混为一谈招致了不必要的纷扰.不同类的量之间运算无意义,与度量制的选取无关,更不影响数的运算意义.这就好比“2cm+(2cm)2”无意义,但显然我们不能据此断言“此处单位(cm)的选取不当”或是“x+x2这一数学运算不合理”.

3.3 “(角度制中)自变量的取值是60进位制的角度,不是10进位制的实数,不符合对应关系的函数定义”

首先,这个断言混淆了单位之间的进率(15)有时也将同类量的不同单位之间的倍数关系描述为“进制”,但与记数法的“进制”表达的含义不同,为区别两方面的用语,此处采用进率的说法.与数值的进位制.其次,一个数是否是实数,由数本身的性质决定,与它是否使用10进制表达无关.

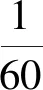
平面角的量值常见有形如1°6'的多单位混合形式的表达,但正如文献[4,P.128]所指出的,“近年来国际上主张采用十进制的数值来表达,而它们的符号则处于全部数值之后,例如:1rad=57.29577951…°;17°15′最好给出为17.25°;53°20′24″最好给出为53.34°”.不难发现,上面例举的式子右边皆为角度制下的10进制数值表达.可见,角度制中,角度数通常表达为10进制数,当然,数的表达可以有多种形式,可选取不同的进位制,也可使用不涉及进位制的其他特定含义的符号表示,如π.

4 小结

初等数学中的三角函数,从直角三角形中锐角对应的三个边长比开始,然后利用直角坐标系推广到任意角,形成三角函数,得到特殊角的函数值,诱导公式,倍角/半角三角函数关系.微积分中利用连续函数和微积分的性质得到三角函数的定义,也得到一系列的函数性质公式.在弧度制下,初等数学中得到的公式与微积分中得到的公式,在形式上高度一致.然而,两者的发展线索不完全有逻辑的上下游关系.由此可见,引入弧度并非是某种不利与便利之间的选择.“在解析运算中,弧度制是很方便的,这一点以后会变得很清楚.但是,在实用中,弧度制又颇为不便,因为π为无理数.所以如果我们在圆周上把单位角,即1弧度的角,一次次地标出来,它决不会回到圆上原来的点.而在建立普通的角度制时就是让它在1度继续标出360次后或90°继续标出四次后,能回到原来的位置”[13,P.285].幸而,关于弧度制的一些误读也正在被澄清.正如文献[14,P.191]所提及的“在弧度先生看来,他们俩(17)此处指弧度制与角度制.除了‘单位’不同外,没有本质上的差别,而且还关系密切”.

“学生对数学的认识和理解在很大程度上也要依靠数学课堂教学”[15],因此教师在数学课堂教学中应尽可能地严谨,处理好数学的逻辑性与历史性之间的关系,体现出“数学的本质”.当然,教学过程不可能完全遵循演绎逻辑的方式去梳理教学内容,学生的认知方式以及有效教学的原则也提示我们,有些教学内容确实需要作适度教学处理,特别是一些不易理解或者不适合在当下“死磕”而应日后“细品”的内容.例如北师大版必修二教材[16],先引发对角度的度量与长度的度量之间关系的思考,再明确弧度数的绝对值等于该角所对的弧长与半径之比,辅之以两种度量制下量值的转化等内容的叙述,给出了弧度制中的关键信息,没有刻意对角度制局限性和弧度制的优越性进行评断.为了说明教学内容的必要性而放大其合理性和必然性,是不合适的.使用弧度制的真实合理性,在高中阶段不见得能完全解释,然而要避免用事实背景不清的内容来辅证,以免给学生带来不必要的误读.