应力波在吊索-梁结头处的传播规律

陈 木, 李 周, 王荣辉*

(1.华南理工大学土木与交通学院，广州 510641；2.中建科工集团有限公司, 深圳 518000)

2019年10月，中国台湾宜兰县某跨海拱桥发生倒塌事故，当油罐车经过桥梁时，最先发生断裂的是跨中向右第一根吊索，破坏位置位于吊索与拱肋的连接处，可见实际拱桥结构中拱肋与吊索连接处是易产生损伤或破坏的位置。目前，普通结构动力学在计算桥梁结构动力响应时，只考虑了惯性力作用，而忽略了扰动在结构中的传播过程，但是当扰动传过结构特征尺度所需时间与冲击荷载持续时间相比处于相同甚至更高量级的尺度时，就必须考虑扰动的传播过程[1]，所以普通结构动力学在处理高频冲击荷载作用下的结构动力响应的问题时会有误差，而应力波理论是研究这类问题的最佳工具之一。Guo等[2]对弯梁受轴向冲击荷载的结构动力响应进行了实验和有限元分析。Fan等[3]和Chen等[4]则分别研究了岩石节理处应力波的反射和透射。Chattopadhyay等[5]和Mehmet等[6]则对层合板中应力波传播进行了研究。Dubuc等[7]提出了各向异性板中弹性导波的相位和群速度的解析表达式。应力波理论在工程中应用比较广泛的是结构探伤等方向。比如Hafiz等[8]提出了一种超声尾波对比技术(CWC)用于混凝土应力监测；Wei等[9]研究不同的裂纹模式、位置、深度及转速对非均匀转轴弹性波传播特性的影响；杨卫奇等[10]分析了壳的几何物理参数及撞击加载条件对屈曲行为的影响，同时分析了屈曲过程中的横向惯性效应和应力波效应。

现从应力波理论的角度分析吊索-梁连接处的受力特点，建立了应力波传播的控制方程，并从经典理论和有限元模型两方面对理论进行验证，最后讨论了梁截面尺寸对吊索受力的影响。通过研究可以使桥梁工程师对拱肋与吊索连接处在外部冲击荷载作用下的受力特点有更加清楚的认识，具有一定的工程意义，以期为应力波在结构中的传播规律等更深入的研究提供参考。

1 理论分析

为研究吊索-梁结头处应力波的传播规律，建立了应力波传播的理论模型，如图1所示。理论模型分为3个部分，梁2和梁3的材料和截面相同，E2、A2和I2分别对应的梁2和梁3的弹性模量、截面积和截面惯性矩，E1和A1则分别是索1的弹性模量和截面积，ρ1和ρ2则分别是索和梁的密度，梁与索的夹角为α。

索1端部有入射波u0向上传播，传播至结头处时发生反射和透射，产生的反射波向下传播，包含纵波u1及横波w1。同时，梁2中有透射纵波u2和透射弯曲波w2，梁3中有透射纵波u3和透射弯曲波w3，正负号规定如图1所示，其中，假设各质点纵向位移正方向与波的传播方向相反，即为拉伸波。

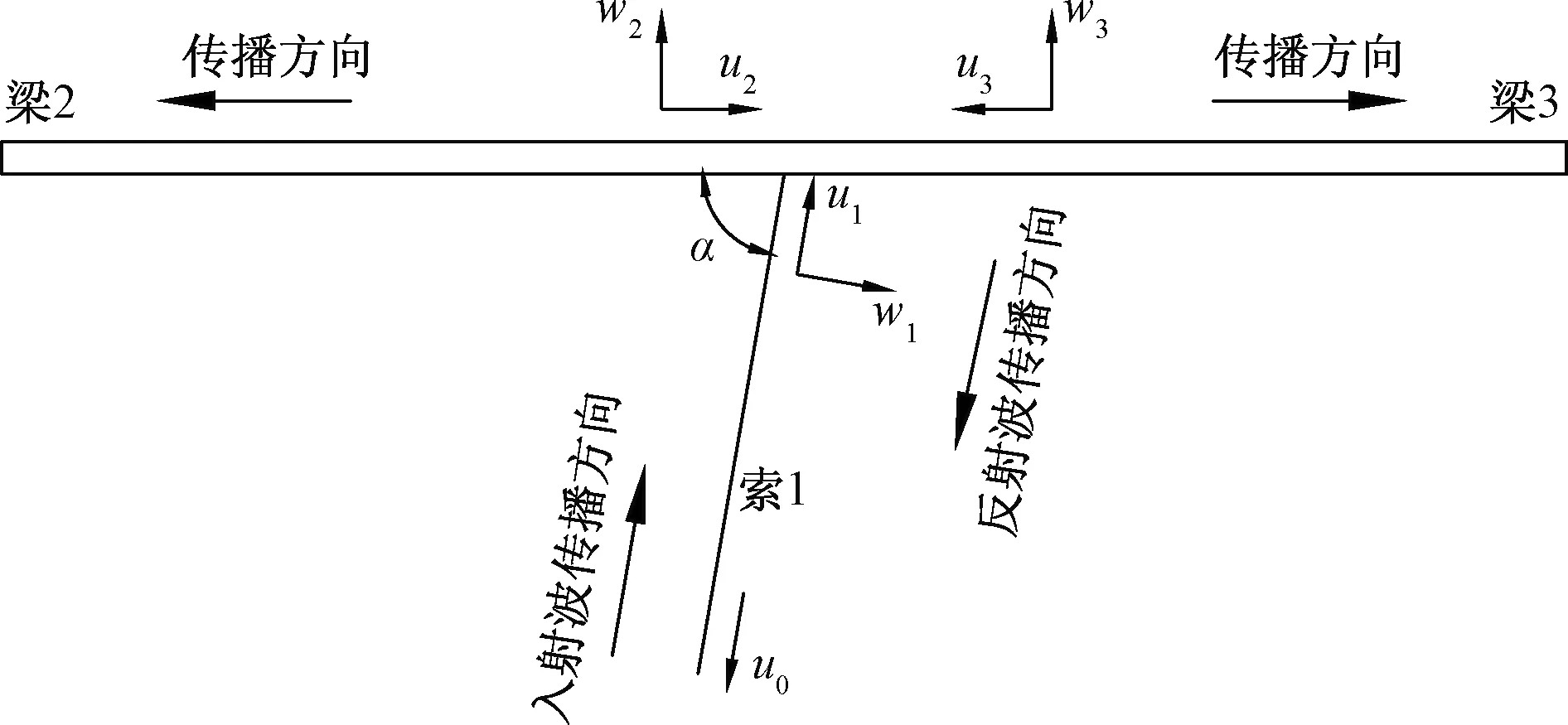
图1 理论模型

假设结头为刚体，入射波由吊索传播至结头处时，结头只有平动，而没有转动，结头的纵向位移为u、横向位移为w，正负号规定如图2所示。

图2 结头位移及转角

由结头与梁和索的位移协调性可知，结头处的纵向位移u和横向位移w与各反射波和透射波质点位移的关系为

(1)

式(1)为主梁-吊索刚性结头处应力波传播的相容方程。吊索在波u0和u1作用下的总轴力为N1，梁2的轴力、剪力和弯矩分别为N2、Q2、M2，梁3的轴力、剪力和弯矩分别为N3、Q3、M3，如图3所示。

图3 结头处受力模型

得到动力学方程为

(2)

式(2)中：mj=ρ2V为结头的质量，ρ2为梁的密度，V为结头的体积。

本构方程为

(3)

式(3)中：G为剪切刚度；As与截面特性相关；x1、x2、x3分别表示索1、梁2、梁3的轴向局部坐标，正方向与图1中u1、u2、u3相同。

入射波u0在结头处产生6类反射波和透射波，为求解控制方程，假定各类波的质点位移函数为

(4)

NBT=Q

(5)

式(5)中：B为待求系数矩阵；N为影响矩阵；Q为与入射波相关的荷载矩阵。

(6)

(7)

(8)

式中：M1～M8分别表示为

(9)

2 数值分析

2.1 与经典理论的对比

经典理论中，梁或索中的纵波在固定边界条件下的反射规律是质点速度为0，质点应力加倍，在自由边界条件下的反射规律是质点应力为0，质点速度加倍，对梁截面积无限大和无限小两种特殊情况进行分析，检验建立的控制方程能否回归到经典理论。

当梁的截面积无限大时，可知结头横向位移w=0，对于各波形的质点位移函数，取n=1且x1=t=0进行分析，由式(1)可知

-(u0-u1)sinα-v1cosα=0

(10)

对于梁-索夹角α=π/2时，由此可知

u0=u1→B0=B1

(11)

式(11)中：B0、B1分别为入射波u0和反射波u1的幅度。吊索端部反射波与入射波叠加后的轴力为

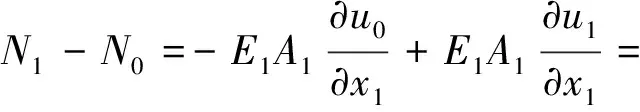
(12)

由式(12)可知，反射波与入射波叠加后产生的轴力是入射波轴力N0的两倍。

吊索端部反射波u1的质点速度为v1，入射波u0的质点速度为v0，叠加后的质点速度为

v=v0-v1=(B0-B1)iω

(13)

所以，吊索端部反射波与入射波叠加后的质点速度为0。这符合纵波在固定边界条件下的反射规律，即质点速度为0，内力加倍。

假设梁的截面积趋近与0，由式(12)可知，反射波与入射波叠加后的轴力N合为0，那么可以得到

B1=-B0

(14)

那么，反射波与入射波叠加后的质点位移为

u0-u1=2u0

(15)

反射波与入射波叠加后的质点速度v为

v=v0-v1=2v0

(16)

这种规律与应力波在自由端边界条件下的反射规律相同，即质点速度加倍，内力为0。

由以上的分析可知，对吊索-梁结头处应力波传播规律所建立的控制方程，在梁截面积无限大和无限小的两种特殊情况下，可以回归到经典理论，从侧面验证了所建立控制方程的正确性。

2.2 梁截面尺寸对结头处应力波传播规律的影响

采用有限元软件ABAQUS建立模型，如图4所示。上部结构采用梁单元进行模拟，吊索采用桁架单元进行模拟。梁截面为正方形，边长为a，长度为10 m，两端采用固结边界条件。索长度为5 m，与梁中点相连接。梁的材料参数为：杨氏模量E1=2.078×105N/mm2，泊松比=0.3，密度=7.85 t/m3；索的材料参数为：E2=1.95×105N/mm2；泊松比=0.3，密度=7.85 t/m3。重物采用半径为0.05 m的圆球，初始冲击速度为5 m/s。

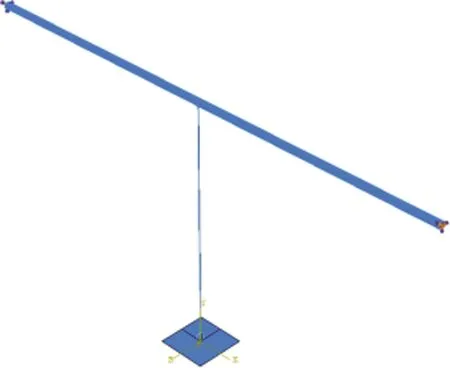
图4 有限元模型

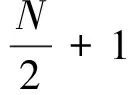
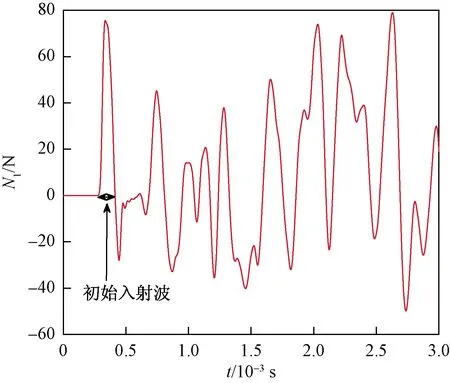
图5 吊索中点位置处轴力N1时程曲线

(17)

式(17)中：k表示时域中初始波信号的离散点的总数，取值为0～N/2，ReX[k]及ImX[k]为快速傅里叶转换(FFT)后的实部及虚部。通过式(17)计算得到每个正弦波及余弦波的振幅及频率后，可根据合成等式计算出初始波形，即

(18)

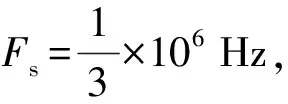
图6 初始波形与拟合波形

式(18)可写为

(19)

式(19)中：c0表示吊索中纵波的传播速度。

为研究吊索上部结构截面尺寸对吊索-梁结头处应力波传播规律的影响，选取a为1、3、5、8、10 mm这5个参数进行数值分析。吊索上端的轴力时程曲线如图7所示。

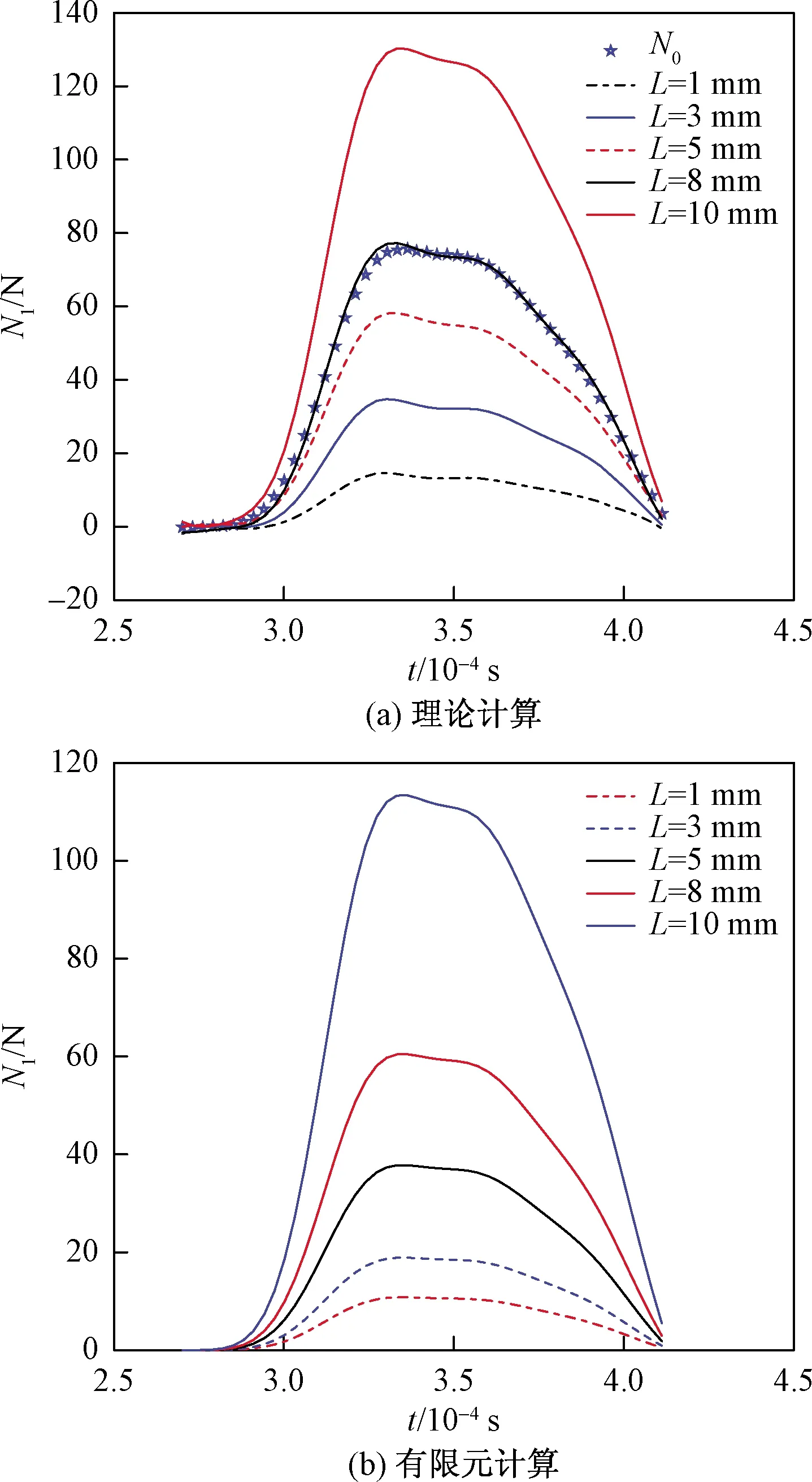
图7 梁截面尺寸a对吊索上端位置轴力N1影响

图7给出了梁截面尺寸a对吊索上端轴力N1影响的理论计算结果及有限元模拟结果。由图7可以看出，梁截面尺寸分别为10、8、5、3、1 mm时，理论计算N1的最大值分别为139.8、131.9、101.4、54.1、4.9 N。而有限元模拟计算结果中，N1的最大值分别为113.3、108.8、83.1、37.3、10.4 N。从图6中可以看出，初始入射波N0的最大值为75.6 N，通过理论计算与有限元模拟计算结果及初始入射波的对比，可以发现以下规律。

(1)理论计算结果中，各种梁截面尺寸参数下，吊索上端轴力时程曲线与初始入射波形相似，本小节中，在反射波和透射波的合成过程中，忽略了各余弦波及正弦波的相位变化，而采用与入射波相同的相位，即可得到与入射波相似的波形，验证了上一小节中关于反射波和透射波与入射波之间相位差需要被忽略的正确性。

(2)理论计算结果与有限元模拟结果有相同的规律，随着梁截面尺寸a的增加，吊索上端轴力N1不断增大。在理论计算结果中，当梁截面尺寸a=3 mm，结头处的反射波对入射波起卸载的作用，而当梁截面尺寸a=5 mm时，结头处的反射波对入射波起加载的作用，当梁截面尺寸a=10 mm时，轴力N1则近似于入射波处轴力N0的两倍。当梁的抗弯刚度逐渐增大时，轴力N1逐渐增大，而质点速度逐渐减小。

(3)有限元模拟结果略小于理论计算结果，但是两种方法的计算结果有相同的变化规律，也验证了理论计算的正确性。

3 结论

针对吊索-梁结头处应力波的传播规律，依据内力平衡性和位移协调性建立了控制方程，假设各反射波及透射波的波形方程，并将波形方程代入控制方程中，可求解出各反射波及透射波的波形，同时建立了吊索-梁结构受小球冲击的有限元模型，提取了吊索中点的轴力时程曲线，并以其中第一个波峰作为理论计算的入射波。由于该入射波是一组离散数据，不能直接代入控制方程计算，所以采用快速傅里叶转换及合成等式相结合的方法，将这组离散数据转换成25个余弦波和25个正弦波线性叠加而的连续函数。对梁截面无限大和无限小两种特殊情况，将控制方程回归到经典理论。最后，对梁截面尺寸进行了参数分析，讨论了这些参数影响下吊索-梁结头处应力波传播的规律。通过研究可以得出以下几点结论。

(1)当梁截面尺寸无限大和无限小时，所建立的控制方程均能回归到经典理论。

(2)有限元及理论数值分析结果对比可知，理论方法的数值分析结果与有限元分析结果的变化规律比较吻合，验证了理论方法是可行的。

(3)具有典型意义的是随着梁截面尺寸a的不断增大，索上端的轴力N1也是不断增大，所以梁的抗弯刚度对吊索的受力有比较大的影响。