桥台对斜交连续梁桥抗震性能的影响研究
2021-09-23王荣霞曹宏琨王雅静
王荣霞 曹宏琨 王雅静


摘要 以一座三跨连续斜交箱梁桥为背景,应用SAP2000建立全桥有限元模型,采用非线性时程分析方法,研究了纵向地震输入下,桥台及台后填土对不同斜度连续梁桥上部主梁及墩柱内力和位移的影响。结果表明:对于斜交连续梁桥,桥台能够减小主梁惯性力,约束主梁及墩柱的纵向位移,但会增大其横向位移,且斜交角度越大,纵向约束效果越弱,横向位移越明显;桥台作用一方面会加剧斜交连续梁桥上部主梁的旋转效应,另一方面会使得两个桥墩出现不均衡受力,斜交角度越大,旋转效应越明显,不均衡受力也越明显。建议在进行抗震设计时,应考虑桥台的作用,对不同斜度的斜交连续梁桥进行个性化设计,以提高斜交连续梁桥的抗震性能。
关 键 词 斜交连续梁桥;斜交角;桥台;台后填土;抗震性能;有限元
Abstract With a three-span continuous skew box girder bridge as the background, the research about the influence of abutment and backfill on internal force and displacement of upper main girder and pier column of continuous girder bridge with different skew angles under longitudinal seismic input has been carried out, with the application of SAP2000 to establish a finite element model of the bridge and the nonlinear time history analysis. The results show that the abutments can reduce the inertia force of main girder and restrain the longitudinal displacement of main girder and pier column, but increase its lateral displacement. With the increase of skew angle, the longitudinal restraint effect is weaker and the lateral displacement is more obvious. On the one hand, abutment effect will aggravate the rotation effect of the upper main girder of skew continuous girder bridge. On the other hand, the abutment function causes unbalanced force of the two piers. With the increase of skew angle, the more obvious the rotation effect of the main girder and the more obvious unbalanced force present in the two piers. In order to improve the seismic performance of skew continuous girder bridges, it is suggested that the influence of abutment should be taken into account in seismic design and individualized design of skew continuous girder bridges with different skew angles should be carried out.
Key words skew continuous girder bridge; skew angle; abutments; backfill; seismic capacity; finite element method
0 引言
斜交橋因能够更好的适应地形及路线走向,近些年被国内外各等级公路大量采用[1],且大多数建于高烈度区[2],因此其抗震设计显得更为重要,有必要对其抗震性能进行深入细致的研究。目前,国内外学者在斜桥抗震方面进行了较多的研究,主要集中于以下几个方面:1)不同斜交角度的斜桥动力特性的研究[3-4];2)碰撞作用对斜梁桥地震响应的影响[5-6];3)斜交角、伸缩缝、挡块、支座等影响参数的分析[7-9]。但上述相关文献均未考虑桥台的影响,且其研究对象多集中于简支斜交梁桥,对连续斜交梁桥研究较少。
桥台作为桥梁结构重要的组成部分,支承桥梁上部结构和路堤相衔接,能够抵抗台后填土压力,并将上部结构传递下来的荷载有效地传递到台后填土中。有研究表明,桥台、台后填土与主梁之间的相互作用在强震作用下能明显改变桥梁地震响应[10]。因此桥台在桥梁抗震设计中不应被忽视。然而以往对桥梁抗震性能研究中,大部分都没有考虑桥台以及台后土体的作用[3-9],这样会导致桥梁其他部分构件的地震需求偏于保守,例如导致墩柱和基础自身受力偏大,需进行加强设计,从而造成了不必要的浪费[11]。文献[12-14]虽然研究了桥台对连续梁桥抗震性能影响,但也都只是局限在于正桥,对斜桥的相关研究尚未见报道。
众所周知,斜交连续梁桥受力特性与正桥相比有明显不同,在地震作用下,桥台对斜交连续梁桥的影响将比正桥更为复杂。而在国内的斜桥设计中,设计人员往往不考虑桥台以及台后填土对斜交连续梁桥的抗震作用,并且在我国《公路桥梁抗震设计细则》JTG/T B02-01—2008中也没有明确规定如何计算和模拟桥台及台后填土的相互作用[15]。因此本文针对桥台对斜交连续梁桥抗震性能的影响研究对此类结构的抗震设计具有的重要指导意义。
1 工程背景
以某座实桥作为计算实例,该桥为预应力钢筋混凝土斜交连续小箱梁桥,跨径为3×35 m,斜交角为20°,设计荷载为公路-Ⅰ级,桥面宽度为净11+2×0.5 m防撞护栏,上部主梁由 4片小箱梁联结组成,支座采用盆式橡胶支座,下部结构桥台采用双柱式桥台,桥墩采用单排双柱式墩,全桥纵断面如图1所示。Ⅰ-Ⅰ横断面图和桥台侧面图如图2和图3所示。桥址地处Ⅱ类场地,按地震烈度8度设防。
2 有限元模型
本文以上述实际工程为依托,采用大型通用有限元程序sap2000[16]建立多个斜交角度(0°~60°,间隔相差10°)的三跨连续斜交箱梁桥模型。
2.1 有限元模型的建立
上部结构采用精细化建模,主梁的顶板、底板、腹板均采用Shell单元进行模拟;桥台采用Shell单元;盖梁、桥墩、桩均采用Frame单元;桩周土体采用弹簧单元,其刚度应用“m”法计算得到[17];盆式支座采用非线性连接单元来模拟,其纵向、横向、竖向3个方向的刚度依据文献[18]计算设定。因全桥结构对称,为显示清晰可见,以下仅示出半桥有限元模型如图4所示。
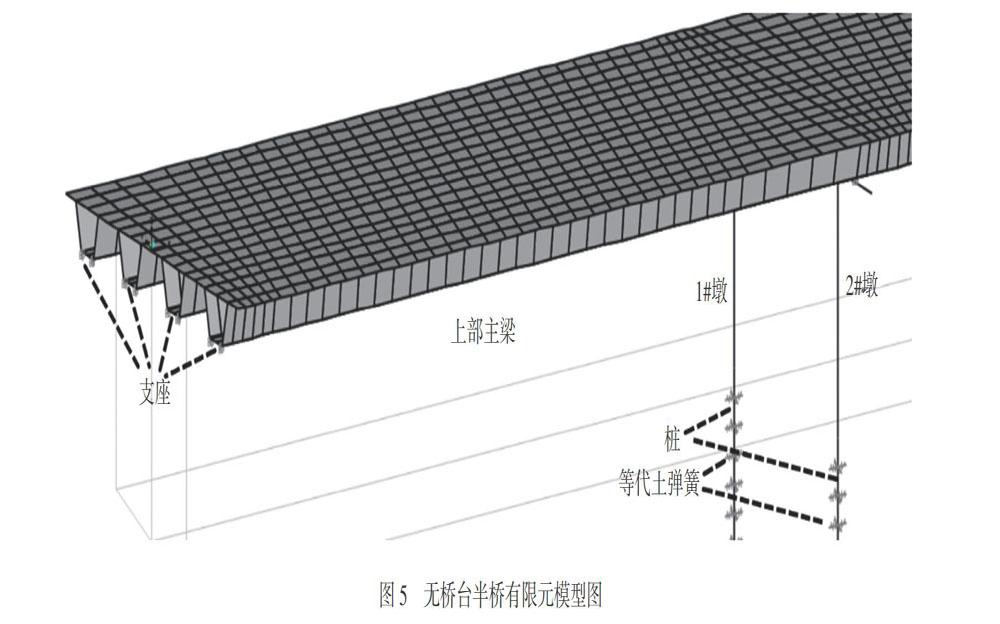
为将计算结果进行对比,利用上述同样的建模方法,建立无桥台的斜交连续梁桥有限元分析模型(如图5所示),但该模型不考虑桥台的作用,也不考虑碰撞效应。边界条件仅模拟盆式支座的刚度,以及桥墩下的桩周土体的作用,模拟方法与上述有桥台情况相同。
在模型中,桥台与台后土体相互作用及桥台处与主梁的碰撞作用的模拟如下所述。
2.2 桥台与台后土体相互作用模拟
本文中桥台采用Aviram等[19]提出的简化弹簧系统模拟(如图6所示)。该系统包括台后填土作用及与主梁碰撞作用。
我国现行规范[15]中没有明确规定如何模拟和计算桥台与台后填土的相互作用。高玉峰[20]结合Shamsabadi等[21]研究成果并在文献[22-23]基础上,考虑了不同桥台高度和台后填土类型,提出了一种新型弹塑性力-位移关系模型,使该模型更符合实际情况。因此本文采用该弹塑性桥台力-位移关系模型(如图7所示)。其中桥台刚度[kabut]及台后填土的极限抗力[Pabut]按公式(1)~(2)计算确定:
2.3 桥台处与主梁碰撞的模拟
3 地震波的选取
本文从美国太平洋地震工程研究中心(PEER)中的数据库中选取了3条地震波(如表1所示)。该桥地处Ⅱ类场地,设防烈度为8度,进行时程分析时,将地震动进行调幅为0.2g,地震激励仅沿纵桥向输入,不考虑竖向和横桥向的地震动的作用。
4 计算结果及其分析
模型计算工况有2种:有桥台(考虑碰撞效应)和无桥台。计算结果包括:上部主梁的纵、横向最大位移;主梁的最大转角;墩柱顶部纵、横向最大位移;以及墩柱底部最大弯矩和最大剪力等。
4.1 上部主梁的反应
4.1.1 上部主梁的纵向位移
表2列出了有无桥台2种工况下,不同斜度的斜交连续梁桥,上部主梁钝角处和锐角处的纵向最大位移数据,以及有无桥台两种工况下,上部主梁锐角处纵向位移相差百分比,上部主梁钝角处纵向位移相差百分比。
从图9中可以看出,在无桥台的工况下,随着斜交角度的增加,上部主梁的纵向最大位移仅发生微小的改变,当斜度为60°时,主梁纵向最大位移仅比0°(正桥)减小0.58%,并且主梁的钝角处与锐角处的位移基本保持一致。
而在有桥台的工况下,当斜度小于40°时,主梁的纵向位移随斜度的增加而大幅度增大;而当斜度大于40°时,这种趋势开始放缓,并在斜度为60°时,达到最大值为0.151 m,相比于0°(正桥)增大了32.86%。并且在图9中还能明显看出,随着斜度的增加,主梁钝角处纵向位移逐渐大于锐角处。其中斜度为50°时,两者最大相差6.83%。由此说明,主梁钝角处与桥台发生碰撞反应最严重。
对比有无桥台两种工况下的主梁纵向位移数据,可以发现有桥台工况下,各斜度的斜交连续梁桥主梁纵向最大位移,均小于无桥台工况。其中在斜度为0°(正桥)时,有桥台工况下的主梁纵向最大位移,比无桥台工况下最大减小26.58%,可见桥台及台后土体能够分担一部分主梁惯性力,从而约束主梁在地震作用下的纵向位移,并且降低了主梁发生纵向落梁的风险,这与文献[12-13]结论一致。
4.1.2 上部主梁的横向位移
表3列出了有无桥台2种工况下,不同斜度的斜交连续梁桥,上部主梁的横向最大位移数据。并根据表3数据,绘制了在2种不同工况下,主梁横向最大位移与斜交角度的关系曲线图(如图10所示)。 从图10中可以看出,在无桥台的工况下,主梁的横向最大位移,随斜度的增加而缓慢增大,当斜度为60°时,横向位移达到最大为0.026 m。
而在有桥台的工况下,当斜度小于30°时,主梁的横向最大位移随斜度的增加而快速增大。而当斜度大于30°时,这种增长趋势开始放缓,并在斜度为60°时,达到最大值为0.061 m。
对比2种工况,可以发现明显不同,当斜度大于0°(正桥)时,有桥台工况下的主梁最大橫向位移明显要大于无桥台工况,其中在斜度为50°时,两工况下的主梁横向位移相差最大,有桥台是无桥台的2.71倍。这是由于台后土体被动土压力,以及主梁与桥台的碰撞力共同作用,从而使主梁产生横向偏移的效应,并且随着斜度的增加这种横向偏移效应越明显,增大了斜交连续梁桥发生横向落梁的风险。
当地震激励仅沿顺桥向输入时,在斜度为0°(正桥)时2种工况下的主梁横向最大位移均为0。可见当仅考虑顺桥向地震波作用时,有无桥台对正桥上部主梁横向位移无影响。
4.1.3 上部主梁的旋转反应
为分析桥台作用对上部主梁的旋转反应,在有限元软件时程分析中的一系列主梁水平旋转角度结果中,选取其中的最大值作为上部主梁峰值转角数据。
表4列出了有无桥台2种工况下,不同斜度的斜交连续梁桥,上部主梁峰值转角数据。并根据表4数据,绘制了在2种不同工况下,主梁峰值转角与斜交角度的关系曲线图,如图11所示。
在无桥台工况下,上部主梁峰值转角随斜度的增加,仅发生微小的变化,其中在斜度为30°时,主梁最大峰值转角也只有0.001 4 rad,由此说明,在无桥台作用下并且地震动仅沿顺桥向作用时,斜交连续梁桥上部主梁的旋转效应很小。
而在有桥台的工况下,上部主梁峰值转角随斜度的增加而逐渐增大,在斜度为60°时,上部主梁峰值转角达到最大值为0.006 7 rad,此时的峰值转角是无桥台工况的6.09倍。由此可以说明,在桥台的作用下,会给主梁施加旋转力矩,从而导致斜交连续梁桥上部主梁发生旋转效应,并且随斜度的增加,这种旋转效应越明显。因此应采取合理设置来减小主梁的旋转效应。
4.2 下部墩柱的反应
4.2.1 墩顶纵向位移
表5列出了有无桥台2种工况下,不同斜度的斜交连续梁桥,墩柱顶部纵向最大位移数据。并根据表5数据,绘制了在2种不同工况下,墩顶纵向最大位移与斜度的关系曲线图,如图12所示。
从图12中可以看出,在无桥台的工况下,墩顶纵向最大位移随斜度的增加而逐渐减小,当斜度为60°时,达到最小值为0.112 m,相比于0°(正桥)减小了8.94%。
而在有桥台的工况下,墩顶纵向最大位移随斜度的增加而逐渐增大。当斜度为60°时,墩顶纵向位移达到最大值为0.108 m,相比于0°(正桥)增大了38.46%。并且还能明显的看出,随着斜度的增加,2#墩顶纵向最大位移逐渐大于1#墩,其中在斜度为50°时,两墩顶纵向位移最大相差11.58%。由此可以说明,在桥台的作用下,会导致斜交连续梁桥的桥墩,在地震反应下纵向延性需求不同。
对比2种工况,可以明显看出,在有桥台工况下,各斜度斜交连梁桥的墩顶纵向最大位移,均小于无桥台的工况。并且随着斜度的增大,两工况下的墩顶纵向最大位移差距逐渐减小。其中在斜度为0°(正桥)时,有桥台工况比无桥台工况减小36.59%;而在斜度为60°时,有桥台工况比无桥台工况减小3.57%。由此可说明,在有桥台的作用下,能降低地震纵向作用下墩柱的纵向位移,这与文献[14]结论一致。
4.2.2 墩顶横向位移
表6列出了有无桥台2种工况下,不同斜度的斜交连续梁桥,墩柱顶部横向最大位移数据。并根据表6数据,绘制了在2种不同工况下,墩顶横向最大位移与斜度的关系曲线图,如图13所示。
从图13中可以看出,在无桥台的工况下,墩顶横向最大位移随斜度的增大,呈现波浪式逐步增大,当斜度达到60°时,墩顶横向最大位移达到最大值为0.023 m。
而在有桥台的工况下,当斜度小于30°时,墩顶横向最大位移随斜度的增加而快速增大;而当斜度大于30°时,这种趋势开始放缓,并在斜度为60°时,墩顶横向位移达到最大值为0.049 m。
对比2种工况,可以发现有桥台作用下并且斜度大于0°时,墩顶横向最大位移明显大于无桥台工况,并且随着斜度的增加,两工况下的墩顶横向最大位移差值越大。其中在斜度为60°时,两工况最大相差53.06%。这是由于存在桥台的作用,使上部主梁产生横向偏移效应,从而导致墩柱横向位移增大。
4.2.3 墩柱底部反力
表7列出了2种工况下不同斜度的斜交连续梁桥,墩柱底部最大弯矩和最大剪力数据。并根据表7数据,绘制了在2种不同工况下,墩底最大弯矩与斜度的关系曲线图(如图14),以及墩底最大剪力与斜度的关系(如图15)。
从图14和图15可以看出,在无桥台的工况下,墩底最大弯矩以及最大剪力,随斜度的增大而逐渐减小,当斜度达到60°时,墩底最大弯矩和最大剪力都达到最小值,分别为8 256.61 kN·m和1 315.69 kN,相比于0°(正桥)分别减小了6.99%和5.73%。
而在有桥台的工况下,墩底最大弯矩以及最大剪力,却随斜度的增加而逐渐增大,当斜度为60°时,墩底最大弯矩和最大剪力都达到最大值,分别为8 529.85 kN·m和1 350.88 kN,相比于0°(正桥)分别增大了57.05%和42.25%。并且还能明显发现,随斜度的增加,1#墩与2#墩呈现不均衡受力状态,并且斜度越大,两者相差越大,当斜度达到60°时,2#墩底最大弯矩和最大剪力,分别比1#墩大8.62%和6.9%。从而会导致在地震作用下,一侧墩柱先进入塑性破坏状态,增大了斜交连续梁桥发生倾斜倒塌的风险。
对比有无桥台两种工况还能看出,在斜交角小于50°时,有桥台工况下的各墩底最大弯矩和最大剪力均小于无桥台工况。由此说明,在有桥台的作用下,会减小桥梁构件的受力,从而减少不必要的浪费。
5 结论
通过本文的计算分析,可以得到如下结论。
1)桥台能够分担一部分主梁的惯性力,从而约束主梁的纵向位移,同时减小墩柱的纵向位移。但对于不同斜度的斜交連续梁,其斜交角度越大,桥台的约束效果越弱。
2)对于斜交连续梁桥,在桥台的作用下,会加大上部主梁的横向偏移效应,以及墩柱的横向位移,并且随着斜度的赠加,这种横向偏移效应越大。
3)桥台的作用,一方面会加剧斜交连续梁桥上部主梁的旋转效应;另一方面使得两桥墩出现不均衡受力,并且随着斜交角度越大,旋转效应越明显,不均衡受力也越明显。
4)建议在进行抗震设计时,应考虑桥台的作用,对不同斜度的斜交连续梁桥进行个性化设计,以提高斜交连续梁桥的抗震性能。
参考文献:
[1] 黄金翠. 地震作用下斜交梁桥旋转特性的初步研究[D]. 重庆:重庆交通大学,2011.
[2] 崔琛. 基于IDA的斜交桥地震易损性分析[D]. 北京:北京交通大学,2018.
[3] MENG J Y,GHASEMI H,LUI E M. Analytical and experimental study of a skew bridge model[J]. Engineering Structures,2004,26(8):1127-1142.
[4] GHOBARAH A A,TSO W K. Seismic analysis of skewed highway bridges with intermediate supports[J]. Earthquake Engineering & Structural Dynamics,1973,2(3):235-248.
[5] 王軍文,沈贤,李建中. 地震作用下斜交简支梁桥旋转机理及斜度影响研究[J]. 桥梁建设,2014,44(3):32-37.
[6] 石岩,王东升,孙治国,等. 隔震斜交连续梁桥地震反应及环境温度影响研究[J]. 振动与冲击,2014,33(14):118-124.
[7] 卢明奇,郭建虎,杨庆山,等. 斜度和支座剪切刚度对斜交连续梁桥自振周期的影响[J]. 地震工程与工程振动,2014,34(增刊):379-382.
[8] 湛敏,王军文,闫聚考,等. 三跨斜交简支梁桥地震碰撞反应参数影响研究[J]. 三峡大学学报(自然科学版),2016,38(4):46-50.
[9] 王军文,吴天宇,闫聚考. 斜交简支梁桥地震碰撞反应参数分析[J]. 振动与冲击,2017,36(3):209-214,221.
[10] AVIRAM A,MACKIE K R,STOJADINOVIC B. Effect of abutment modeling on the seismic response of bridge structures[J]. Earthquake Engineering and Engineering Vibration,2008,7(4):395-402.
[11] KAJITA Y,OTSUKA H,FUJIYOSHI Y. A horizontal test and its simulation analysis of the abutment model with backfill soil[C]// 15WCEE. Lisboa:2012.
[12] 李立峰,王辉辉,吴文朋,等. 桥台-填土-结构相互作用对RC连续梁桥抗震性能的影响分析[J]. 世界地震工程,2017,33(2):71-79.
[13] 王翼,李建中. 桥台对连续梁桥纵向地震响应的影响[J]. 同济大学学报(自然科学版),2018,46(4):423-429.
[14] 王辉辉. 考虑桥台—填土—结构相互作用时RC连续梁桥抗震性能研究[D]. 长沙:湖南大学,2015.
[15] JTG/T B02-01—2008,公路桥梁抗震设计细则[S]北京:人民交通出版社,2008.
[16] 北京金土木软件技术有限公司,中国建筑标准设计研究院. SAP2000中文版使用指南[M]. 2版. 北京:人民交通出版社,2012.
[17] JTG D63 —2007,公路桥涵地基与基础设计规范 [M]. 北京:人民交通出版社,2007.
[18] 范立础,胡世德,叶爱君. 大跨度桥梁抗震设计[M]. 北京:人民交通出版社,2001.
[19] AVIRAM A,MACKIE K, STOJADINOVIC B. Guidelines for nonlinear analysis of bridge structures in Califormia[R]. Berkeley:Pacific Earthquake Engineering Research Center,University of California,2008:43-50.
[20] 高玉峰. 考虑碰撞效应的桥梁非线性地震反应特性研究[D]. 成都:西南交通大学,2011.
[21] SHAMSABADI A,ROLLINS K M,KAPUSKAR M. Nonlinear soil–abutment–bridge structure interaction for seismic performance-based design[J]. Journal of Geotechnical and Geoenvironmental Engineering,2007,133(6):707-720.
[22] Caltrans Seismic Design Criteria[s]. Version 1. 7. Sacrameto:Califomia Department of Transportation,2013.
[23] Caltrans Seismic Design Criteria[s]. Version 1. 4. Sacrameto:Califomia Department of Transportation,2006.
[24] 于海龙,朱晞. 地震作用下简支梁桥梁间碰撞的反应性能[J]. 北方交通大学学报,2004,28(1):43-46.
