喉管直径对旋风分离器性能影响的仿真研究

（兰州大学 资源环境学院，兰州 730000）

0 引言

旋风分离器结构简单，制造、维护成本低，运行稳定，广泛用于多相流中颗粒和液滴的收集。其原理是流体切向进入旋风分离器后在分离空间产生旋流运动，颗粒或液滴在离心力作用下被甩向壁面。在旋流的外部，气体向下运动，把分离到器壁的颗粒或液滴带到旋风分离器的底部，气体反向向上运动，形成内部旋流，从溢流管上部排出［1］。

许多研究表明，流体的旋转流动产生涡［2］，涡使得旋风分离器的流场不稳定［3］，产生旋进涡核［1］，导致能量耗散［4］，颗粒的分离效率降低［5］。所以，旋风分离器中涡结构的研究至关重要。Iozia等［6］提出了涡核直径拟合方程，又基于颗粒平衡理论预测分割粒径d50。结果表明，涡核直径受入口面积和溢流管直径影响很大。Peng等［7］的研究指出外旋涡的体积对颗粒所受的离心力起决定性作用，故涡核直径对旋风分离器的性能影响显著。Hoekstra等［8］采用激光多普勒测速技术测量具有不同溢流管直径旋风分离器内部的切向速度分布，表明溢流管直径减小，涡核直径减小。Brar等［9］减小溢流管直径使得颗粒收集效率提高，但压降增加明显，多位学者［10-13］得到了相同的结果。Kumar等［14］设计了锥形溢流管旋风分离器，增加锥形溢流管的锥角使得分离效率增加，同时压降显著增大。以上学者的研究显示溢流管的直径和形状会显著影响旋风分离器的涡核直径，进而影响其性能。

总而言之，许多学者通过改变旋风分离器溢流管直径和形状来研究其对涡核直径的影响，但是通过在溢流管上部气流出口处外加结构控制涡核直径的研究甚少。本研究在普通Lapple型（d/D=0.5）旋风分离器气流出口处外加了d/D=0.1，0.2，0.3，0.4四种不同直径的喉管结构，确定相应的涡核直径大小，以及切向速度、轴向速度、径向速度、涡核偏心等流场特性和旋风分离器压降、分离效率的变化。

1 数值模拟

1.1 模拟方法及边界条件

雷诺应力模型消除了各向同性湍流的假设，适用于旋风分离器内部气相流场的模拟，因此本文采用雷诺应力模型（RSM）模拟气相流场的湍流［15］，得到不同喉管直径的旋风分离器内部流场分布。在稳定流场基础上注入颗粒，假设颗粒相为稀相流，可利用LPT模型［15］进行追踪，获得分级效率曲线和颗粒分布。

本研究在普通Lapple型（d/D=0.5）旋风分离器气流出口处外加d/D=0.1，0.2，0.3，0.4四种不同直径的喉管结构，具体尺寸及结构如图1（a）所示。测 量 截 面 选 择 x=0，z=-1.0D，z=-1.5D，z=-2.0D，z=-2.5D，如图1（b）所示。为提高计算精度，所有的网格均为ICEM 17.0绘制的正六面体网格，见图1（c）。求解器采用商业计算软件FLUENT 17.0，气相流体为空气，密度为1.225 kg/m3，黏度为 1.79×10-5Pa·s，颗粒相为碳酸钙，密度为 2 800 kg/m3。边界条件设置见表1。

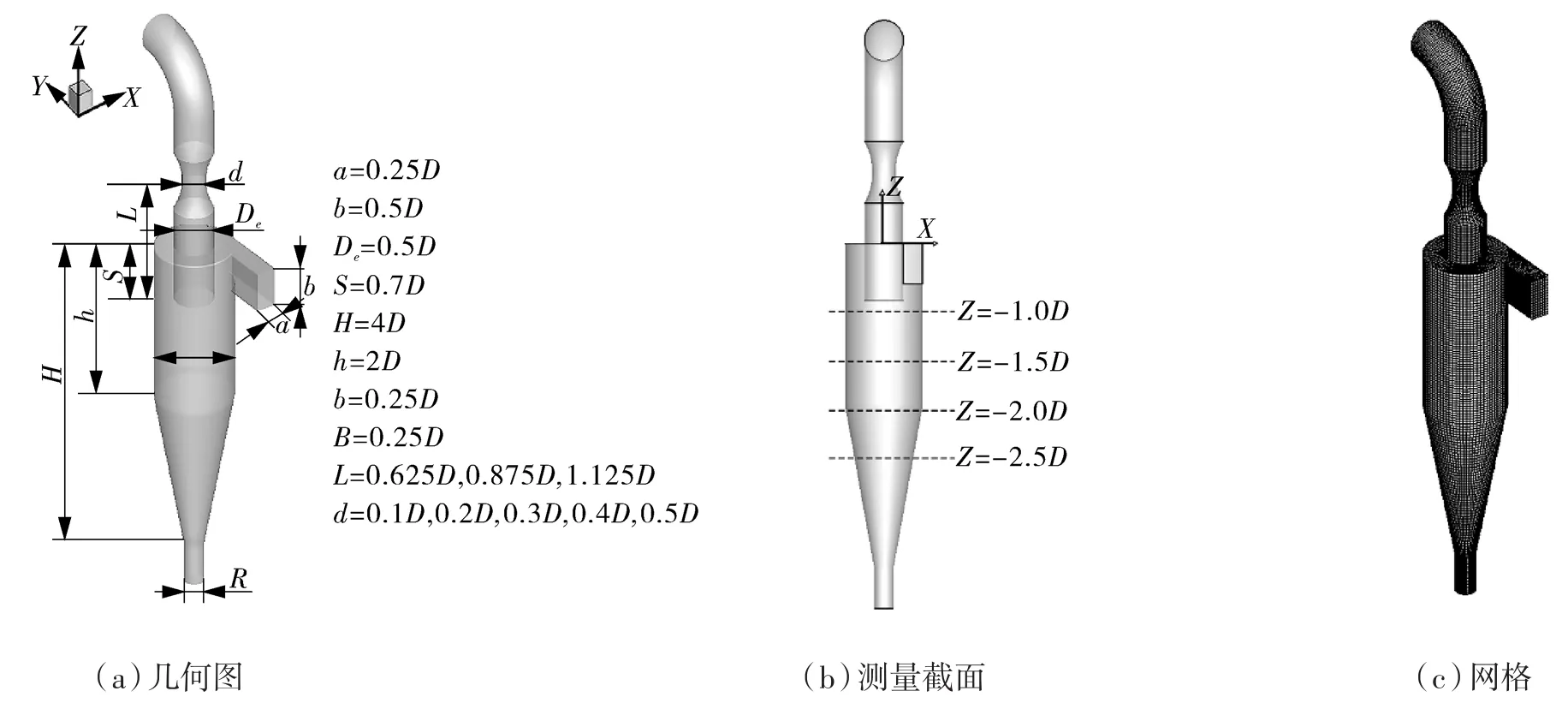
图1 旋风分离器的几何图、测量截面和网格Fig.1 Schematic，measured sections and grid representation of the cyclone separator

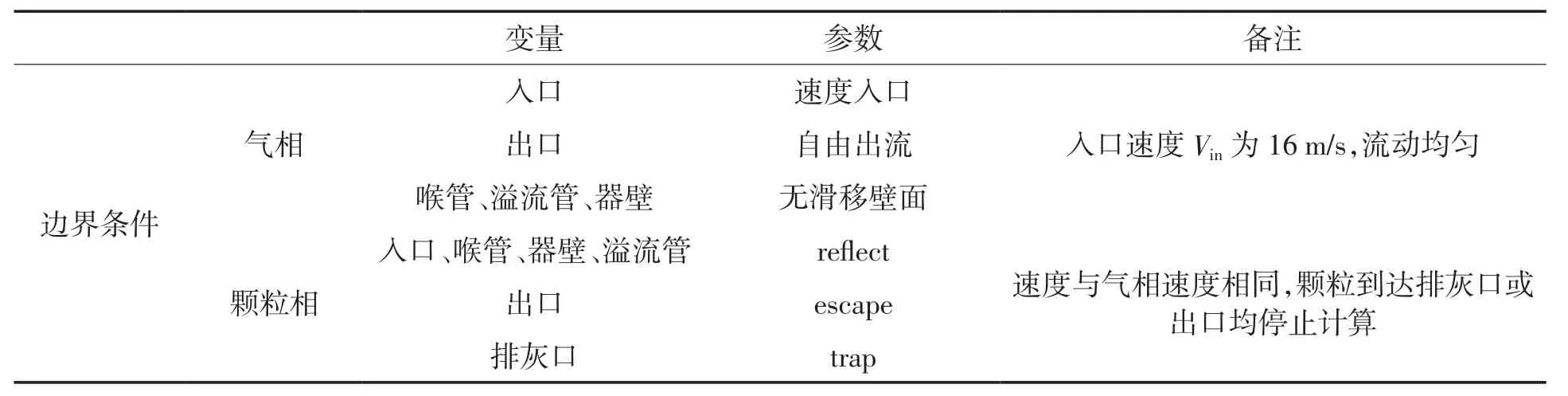
表1 边界条件设置Tab.1 The settings of the boundary conditions

1.2 模型验证

为了验证模拟结果的合理性，本研究选取截面z=-0.625D，-2.0D和-2.5D处数值模拟的切向速度Vt和轴向速度Va结果与Hoekstra的试验结果［16］进行对比，结果如图2所示。从图可以看出，趋势拟合较好，因此可以认为数值模拟的结果是合理准确的。在Hoekstra的试验中，截面z=-2.0D和-2.5D的中心轴处轴向速度曲线平缓，原因可能是因为涡核偏心现象的空间平均效应，即由于涡核进动和激光多普勒测速仪测定的体积有限，使得试验测定的速度曲线变得平滑［16］。

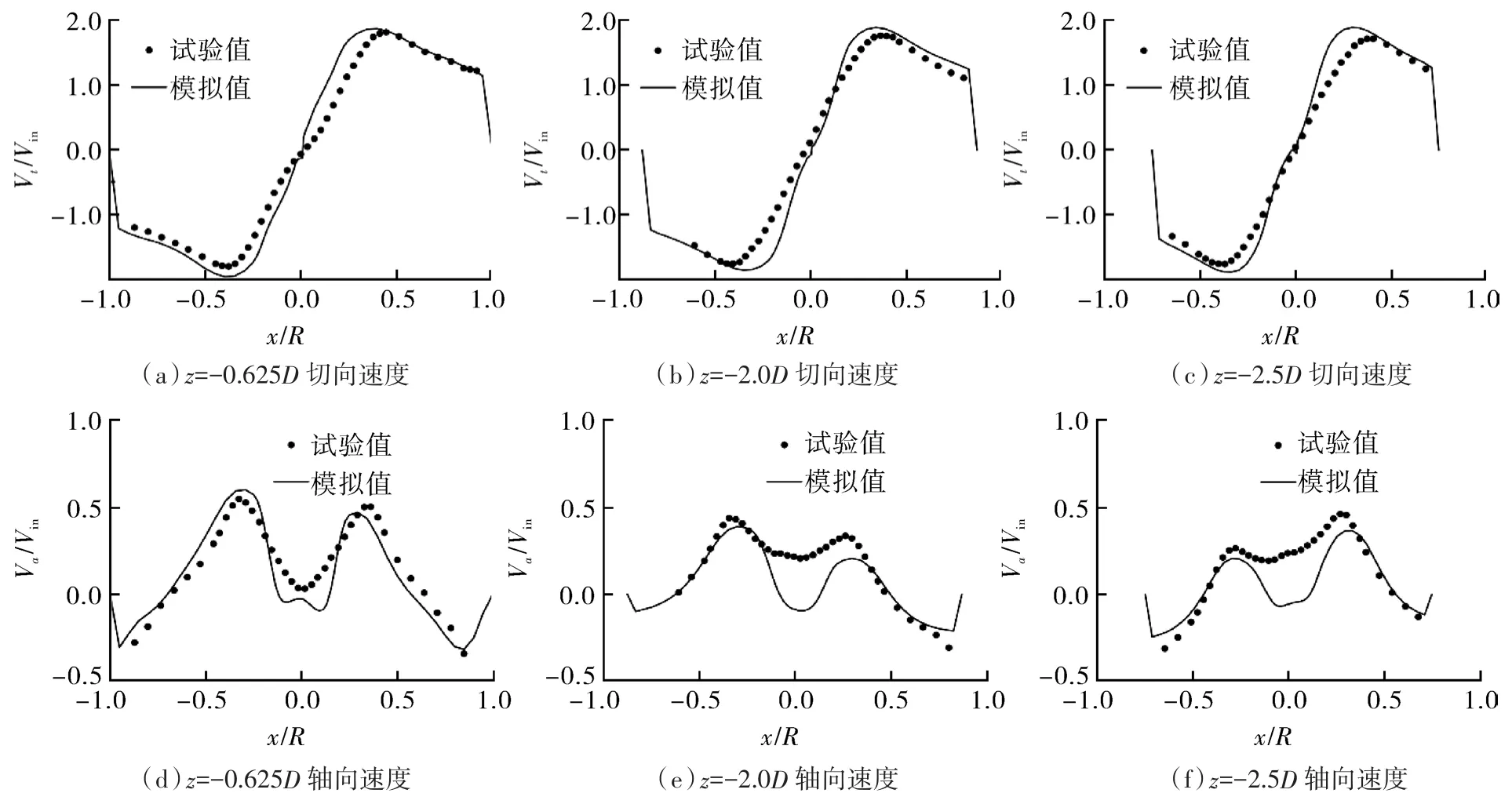
图2 模拟结果与试验结果对比Fig.2 The comparison between the simulation results and the experimental results

2 结果与讨论

2.1 喉管直径对速度场的影响

切向速度分布与颗粒的离心力密切相关，对旋风分离器的分离效率影响很大，图3示出不同喉管直径旋风分离器内切向速度的分布。切向速度沿几何中心轴呈对称分布，径向方向上沿器壁向几何中心轴先非线性增大后线性减小，呈类似M型分布，为标准的兰金组合涡结构［17］，即内旋涡为准强制涡，外旋涡为准自由涡。对于给定的喉管直径，切向速度在轴向方向上的分布类似；随着喉管直径减小，在径向方向上最大切向速度的位置向中心移动，且数值增加。

图3 x=0截面和z=-1.0D测量直线上的不同喉管直径切向速度分布Fig.3 The tangential velocity of different hollow throat diameters in the x=0 section and z=-0.1D measured line

最大切向速度是内外旋涡分界线［18］，图4（a）示出不同喉管直径旋风分离器测量截面的平均涡核直径和平均最大切向速度。由图可知，喉管直径可以控制内旋涡的大小，随着喉管直径减小，涡核直径先逐渐减小，当喉管直径与筒体直径比值为0.3时，涡核直径趋于稳定。内旋涡体积减小，分离空间增大，且切向速度增加，离心力增大，有利于颗粒的收集。

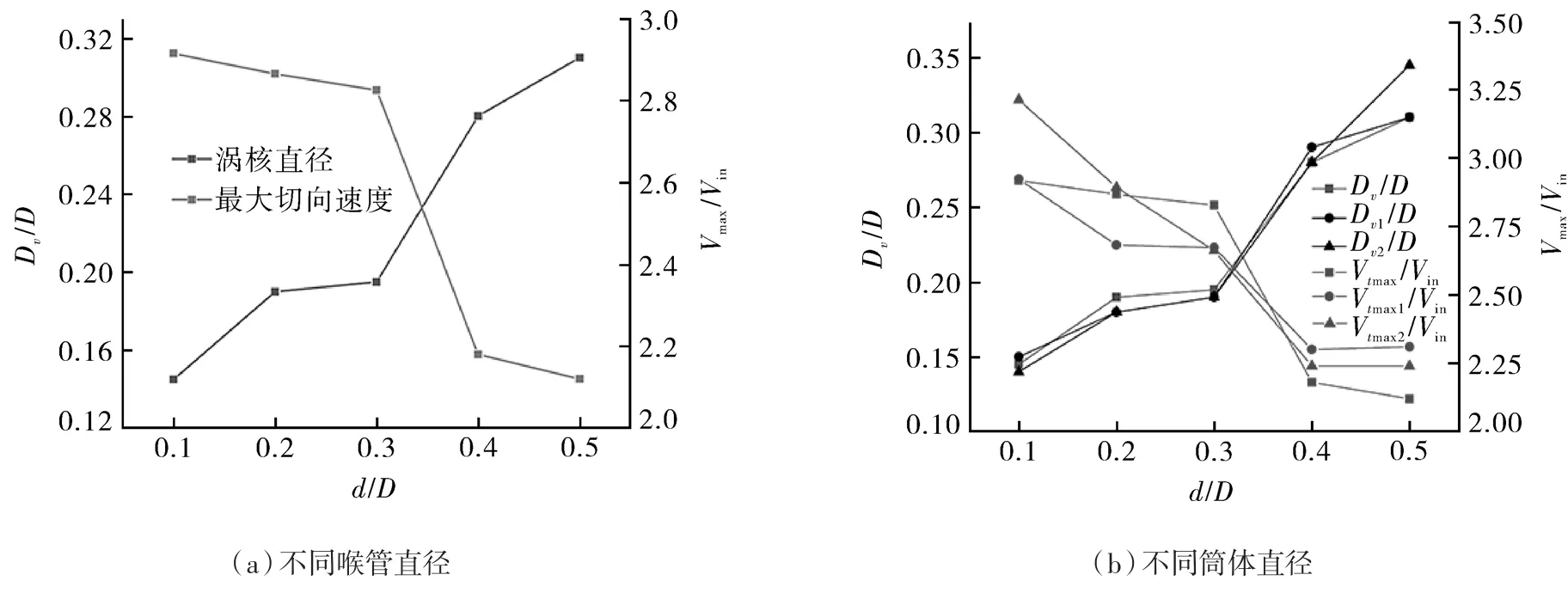
图4 不同喉管、筒体直径旋风分离器的平均涡核直径和平均最大切向速度Fig.4 The average vortex diameter and the average maximum tangential velocity of the cyclone separators in different hollow throat diameters and cylinder diameters

普通Lapple型旋风分离器筒体的直径D=200 mm，考虑到筒体直径放大后涡核直径与筒体直径的比值可能也会放大，改变筒体直径，D1=2.5D=500 mm，D2=4D=800 mm，确定筒体直径放大后旋风分离器的最大切向速度和涡核直径，如图4（b）所示。筒体直径增加，喉管直径仍然可以控制涡核直径的大小，且涡核直径与筒体直径的比值几乎不变，不存在放大效应。喉管结构喉口位置与溢流管下口间的距离可能会影响涡核直径，喉管直径与筒体直径比值为0.3时涡核直径趋于稳定，此条件下改变喉管位置如图5所示，最大切向速度的位置并未发生改变，涡核直径大小几乎没有变化。

图5 x=0截面和z=-1.5D测量直线上的不同喉管位置切向速度分布Fig.5 The tangential velocity of different hollow throat locations in the x=0 section and z=-1.5D measured line

不同喉管直径的轴向速度分布如图6所示，轴向速度在分离空间大致呈对称分布。由图6可知，随着喉管直径减小，轴向速度最大值由溢流管内壁向中心轴线位置移动，与Elsayed等［19］的研究结果一致。当喉管直径与筒体直径的比值减小至0.3时，轴向速度由倒w变为倒v分布，由负压力梯度产生的中央回流区被破坏。回流的产生与旋流强度密切相关，而旋流强度的大小一般由旋流数来表示［20］，由旋流数定义可知，喉管直径减小使得旋流数减小，当旋流数减小到一定程度时回流消失。

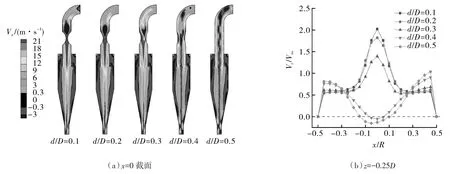
图6 x=0截面和z=-0.25D（溢流管内）测量直线上的不同喉管直径轴向速度分布Fig.6 The axial velocity of different hollow throat diameters in the x=0 section and z=-0.25D （inside the vortex finder） measured line

图7示出不同喉管直径径向速度分布，由图可知，旋风分离器的筒体段和锥体段的准自由涡区，径向速度分布均匀，数值几乎为0，但由于涡核偏心现象的存在，准强制涡区径向速度沿中心轴呈现一正一负交替分布。气流自旋风分离器的筒壁流向溢流管外壁，沿着外壁下行，并直接从溢流管下端逃逸，这种现象被称为短路流［21］。小颗粒容易被短路流携带，从而导致小颗粒的收集效率降低；随着喉管直径减小，短路流量略有增加［22］。

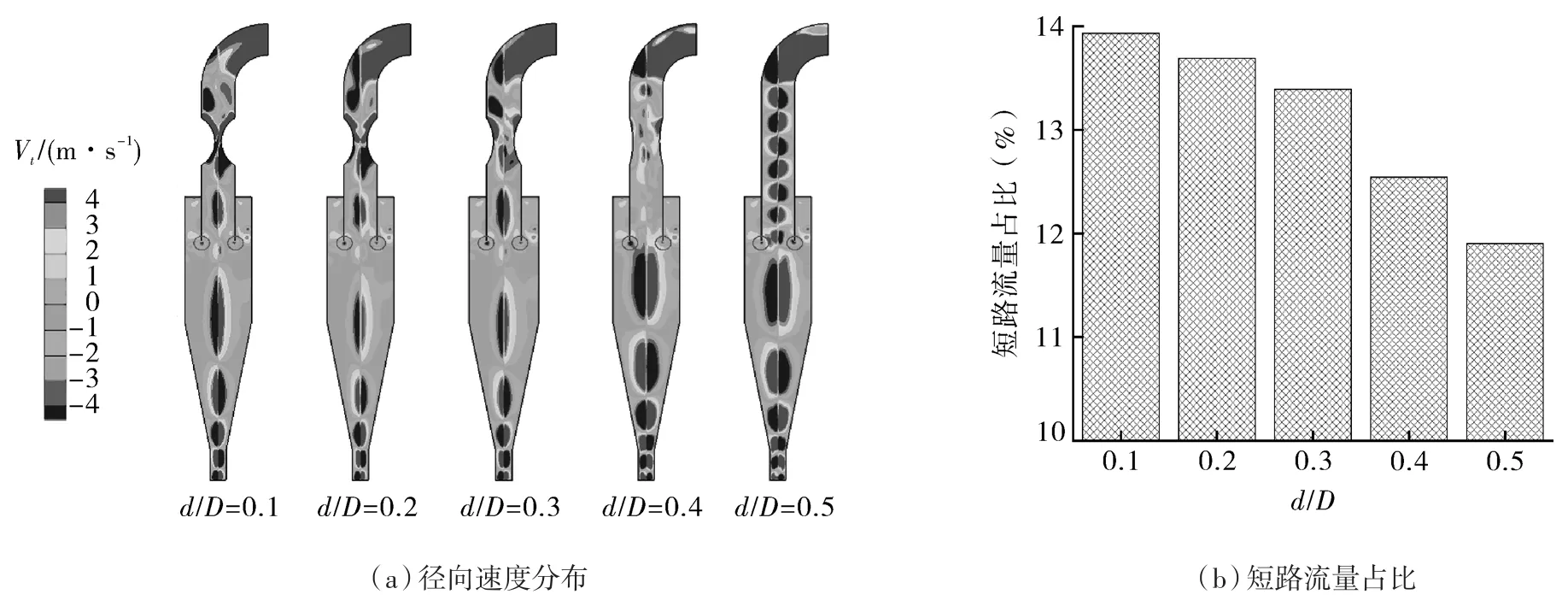
图7 不同喉管直径径向速度分布和短路流量占比Fig.7 The radial velocity and the ratio of the short circuit flow of the different hollow throat diameters

2.2 涡结构及偏心现象

1988年Hunt等［23］提出了Q准则用于涡区域的判定，Gao等［24］利用Q准则对旋风分离器进行等涡面的识别。Q的大小代表了单位体积单位质量的涡具有的能量，图8示出Q=10 000 s-2的三维等值面。由图可知，随着喉管直径减小，三维等值面的当量直径不断减小，能量损失增加。事实上，涡核中心并不是与几何中心完全重合的，而是偏离几何中心，呈现一种准周期性转动，称为旋进涡核［20］。旋风分离器中涡的不稳定性引起流场的不稳定，进而产生旋进涡核［23］，不利于颗粒的分离。

图8 Q=10 000 s-2三维等值面Fig.8 The three-dimensional iso-surface of Q=10 000 s-2

前期研究表明，涡核偏心现象的改善有利于小颗粒的分离［24］。本文以压力最小值点作为涡核的中心点，研究了喉管直径对涡核偏心的影响。图9（a）（b）分别示出了不同喉管直径涡核中心的偏心距在轴向方向上的分布和平均值的变化。由图可知，喉管直径减小，涡核中心的偏心距减小，当喉管直径与筒体直径的比值减小为0.3后，涡核中心的偏心距基本保持稳定。

2.3 喉管直径对分离器性能的影响

压降和分离效率是评价旋风分离器性能的2个重要参数。前者代表能量消耗，后者代表颗粒收集效果。如图10（a）所示，外旋涡区域为高压区，但压降变化相对较小，内旋涡则是旋风分离器产生压降的主要区域，静压沿径向方向由器壁向中心轴逐渐减小。如图10（b）所示，静压压降随着喉管直径减小呈几何数增加，原因在于切向速度增加需要更多的静压转换为动压来维持；而总压压降随着喉管直径的减小增幅不大，原因可能是筒体部分的结构几乎未发生改变，因此筒体内部能量损失的差异主要来源于速度场的不同，而本研究已证实了喉管直径的改变对于旋风分离器内部整体速度大小影响不大。

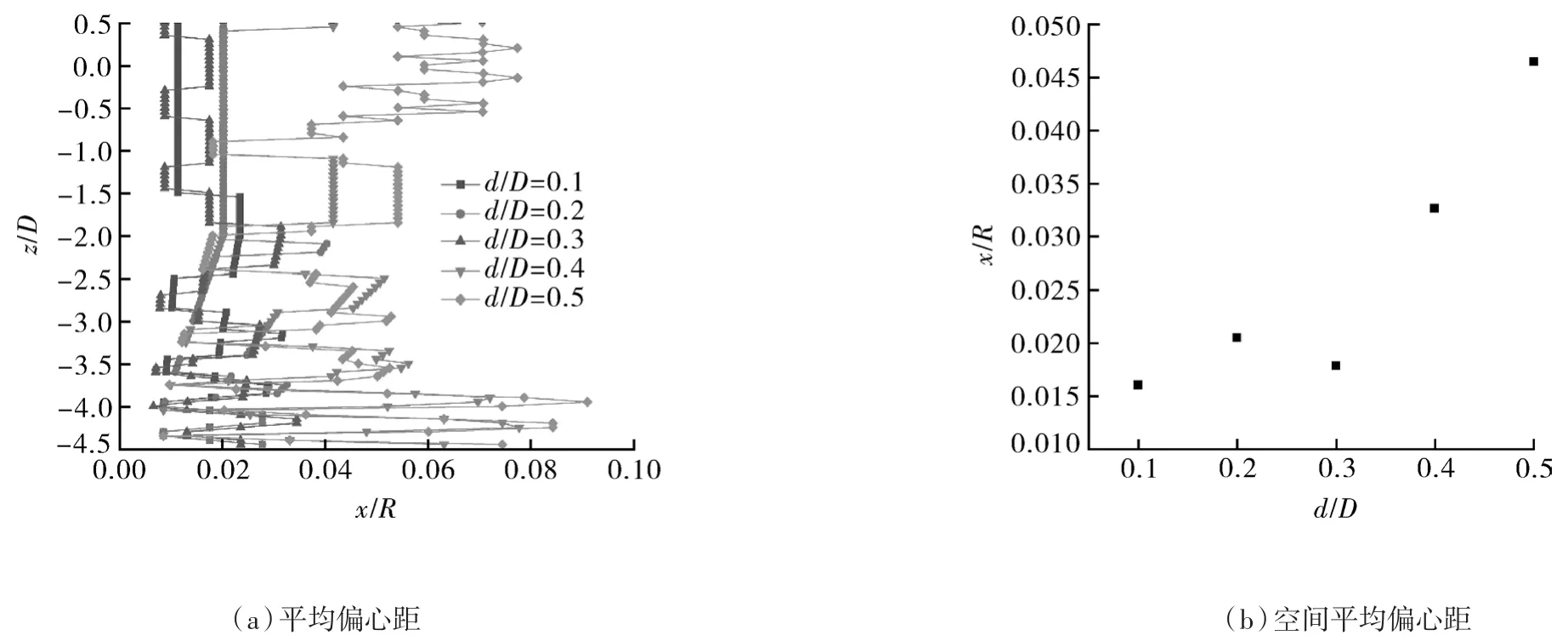
图9 喉管直径对涡核偏心的影响Fig.9 The influence of hollow throat diameters on the vortex core eccentricity

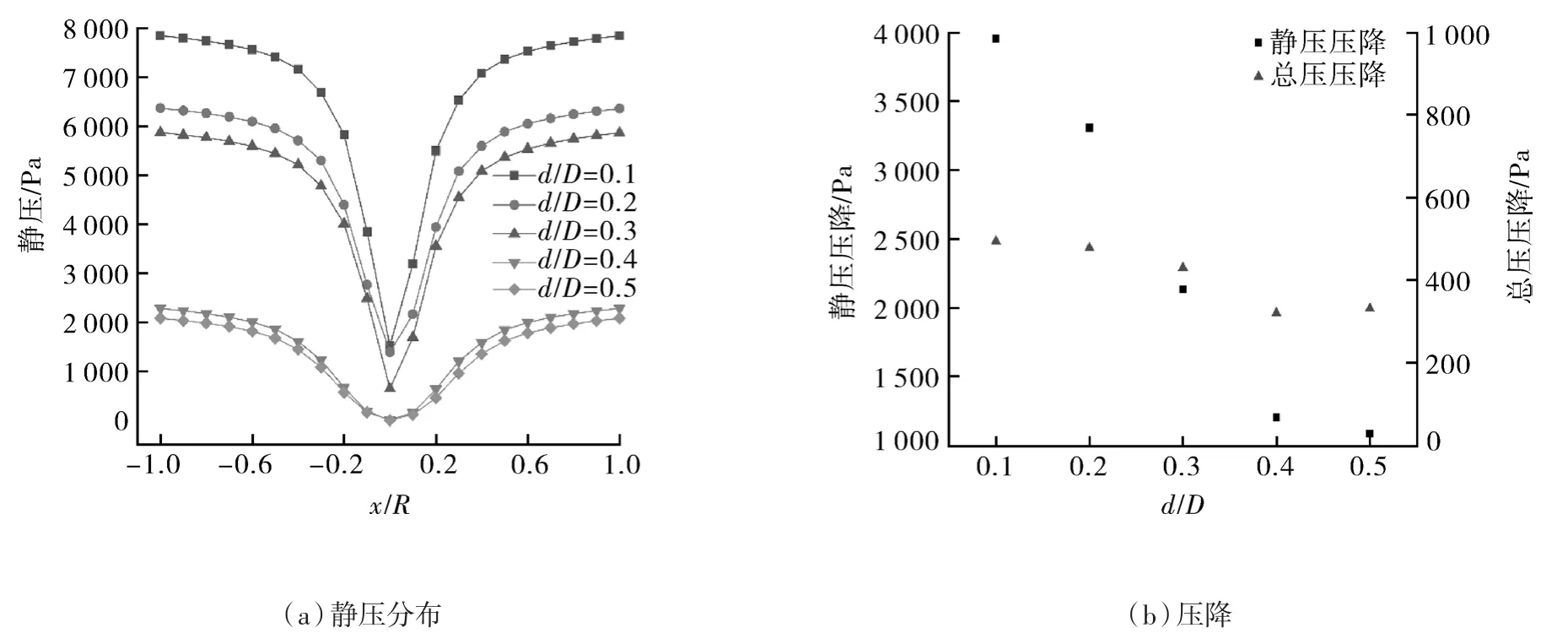
图10 不同喉管直径z=-1.0D测量直线上的静压分布和压降Fig.10 The static pressure of z=-1.0D measured line and the pressure drop of the different hollow throat diameters

图11（a）示出不同喉管直径的分级效率，由图可知，随着喉管直径减小，收集效率增加，原因主要是喉管直径减小，内旋涡体积减小，分离空间增加，切向速度的数值增大，且流场稳定性提高，但当喉管直径与筒体直径比值为0.1时，短路流量增加明显，如图6（b）所示，收集效率反而有所降低。喉管直径改变主要增加较小颗粒（图中A段）的收集效率，当喉管直径与筒体直径的比值为0.2时，与普通Lapple型（d/D=0.5）旋风分离器相比0.5 μm的颗粒收集效率增加高达8%，中等粒径颗粒（图中B段）的收集效率变化较小，2 μm颗粒收集效率仅增加3%左右，当颗粒粒径达到6 μm后（图中C段），收集效率达到100%。选取粒径 0.8，1，1.5，2.5，6 μm 的颗粒。随着颗粒粒径增加，离心力增加，颗粒越容易被甩向器壁，从而被收集。由图11（b）可知，颗粒沿中心轴对称分布，粒径越大的颗粒分布区域越靠近壁面，且溢流管、喉管和出口处均无大粒径颗粒分布。随着喉管直径减小，如图3所示，切向速度不断增加，此时颗粒所受的离心力增加，更易被甩向器壁，使得同粒径颗粒在喉管直径更小的旋风分离器的分离区域更靠近壁面分布。

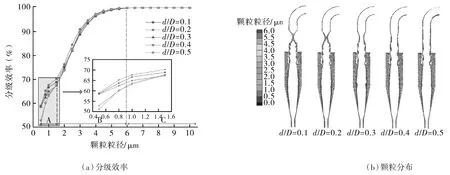
图11 不同喉管直径分级效率和颗粒分布Fig.11 The grade efficiency and the particle distribution of the different hollow throat diameters

3 结论

（1）喉管直径可以控制涡核直径的大小。随着喉管直径减小，涡核直径先逐渐减小，流场稳定性提高，当喉管直径与筒体直径的比值减小到0.3时，涡核直径趋于稳定。同时喉管直径减小，涡核中心的偏心距减小，当喉管直径与筒体直径的比值减小为0.3后，涡核中心的偏心距基本保持稳定。

（2）随着喉管直径减小，最大切向速度向中心位置移动，数值增加；轴向速度最大值由溢流管内壁向中心轴线位置移动，由负压力梯度所产生的中央回流区被破坏，但短路流量略有增加。

（3）总压压降随着喉管直径减小增幅不大。随着喉管直径减小，较小颗粒的收集效率得到明显提升，当喉管直径与筒体直径的比值为0.2时，0.5 μm的颗粒收集效率与普通Lapple型（d/D=0.5）旋风分离器相比增加8%。存在一个较优的喉管直径与筒体直径的比值范围0.2～0.3，在此范围内，旋风分离器分离效率较高，同时压降较低。

总体而言，本研究有助于进一步了解旋风分离器内的复杂流场及性能，并为其结构改善提供指导。