考虑间隙影响的涡旋压缩机转子系统动态特性研究

2021-02-23

流体机械 2021年1期

（兰州理工大学石油化工学院，兰州 730050）

0 引言

涡旋压缩机相比于其他类型的压缩机具有高效、低振和低噪等诸多优点而广泛应用于动力工程、交通运输以及空调制冷等领域。作为涡旋压缩机的主要部件，转子系统的工作状态直接影响着涡旋压缩机的稳定性。制造装配误差、材料变形及磨损等问题造成的运动副间隙，必然导致涡旋压缩机的动不平衡。在涡旋压缩机运行期间，含间隙运动副元素会发生接触失真的现象，接触时产生碰撞，引起非线性冲击载荷，造成运动副的破坏以及影响压缩机系统载荷的正常传递，降低了涡旋压缩机的工作效率和可靠性。

国内外已有诸多针对涡旋压缩机转子系统的相关研究，李超等［1］针对变容量涡旋压缩机曲轴系统，运用多体动力学和有限元方法，计算获得了曲轴各轴承载荷及曲轴应力应变随压缩机转速的变化规律，并对曲轴最大应力应变位置进行了安全性校核；邱海飞［2］通过建立的涡旋压缩机主轴传动系统等效力学模型，应用参数化建模与动态优化方法，获得主轴系统自振频率和振型，为改进主轴的动平衡性能，对主轴平衡重进行了优化设计；余洋等［3］考虑曲轴轴径处存在运动副间隙条件下的动涡旋盘动力特性，分析了动涡旋盘的运动轨迹以及位移变化规律，为运动副间隙影响的涡旋压缩机动平衡设计提供了参考；黄华军等［4］针对小曲拐防自转机构与动涡旋盘连接处存在运动副间隙的情况，分析了间隙数目与间隙大小对动涡旋盘及小曲拐接触力的影响规律，总结了间隙位置的不同对涡旋压缩机动平衡的影响。

上述研究分析了涡旋压缩机转子系统的振动、轴承受力以及运动副间隙对动涡旋盘和防自转机构小曲拐运动特性的影响。但有关运动副间隙对曲轴动态特性的影响、涡旋压缩机含间隙运动副对其瞬态动力性能的影响等方面的研究较少。本文以十字滑环为防自转机构的涡旋压缩机转子系统为研究对象，在考虑运动副间隙的作用时采用非线性弹簧阻尼模型和库仑摩擦力模型，基于多体动力学分析软件，并结合有限元方法，详细分析了运动副间隙下转子系统的瞬态动力特性，可为涡旋压缩机加工制造和装配以及提高转子系统动力特性提供理论依据。

1 涡旋压缩机转子系统模型

转子系统的组成如图1所示，曲轴由主、副轴承支承，曲柄销处由滚针轴承将曲轴与动涡旋盘连接，在运行过程中，电机通过带轮带动曲轴驱动动涡旋盘作公转平动，实现与静涡旋盘的啮合，完成对气体的吸气、压缩及排气过程［5］。

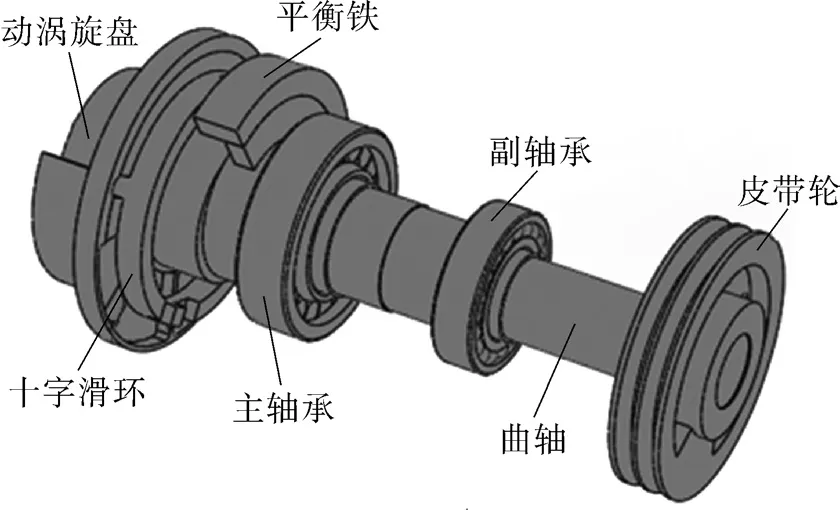
图1 涡旋压缩机转子系统三维模型Fig.1 Three-dimensional model of rotor system for scroll compressor

2 运动副间隙力学建模

在涡旋压缩机运行期间，运动副间隙的存在使得轴与轴承之间的理想接触产生了松动，造成接触失真现象，轴与轴承之间从接触状态到自由运动状态，再到接触状态，整个过程包含着接触与碰撞。旋转副间隙中含有润滑油，可将这种接触考虑为弹簧阻尼模型，根据文献［4］与文献［9］建立接触碰撞模型。

2.1 运动副间隙的矢量模型

如图2所示，在平面旋转铰内引入一个间隙矢量来表达间隙矢量模型［6-8］。

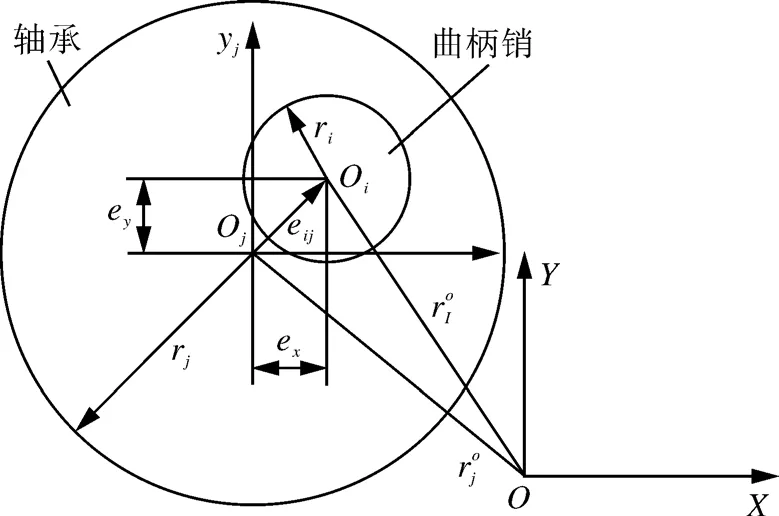
图2 间隙矢量模型示意Fig.2 Schematic diagram of joint clearance vector model

间隙矢量可以反映运动副间隙元素之间的相对位置，可有效处理间隙运动副连接点相对位置的变化，间隙大小用轴承半径与曲柄销半径之差来描述，则：

式中 c——间隙；

rj——轴承半径；

ri——曲柄销轴半径。

定义XOY为广义坐标系，间隙矢量定义在一个局部浮动笛卡尔坐标系xjojyj中，以轴承的回转中心为间隙矢量的基准起始点，矢量方向指向曲柄销和轴承相对运动的接触点，终点为曲柄销的回转中心。由图可得，曲柄销中心与驱动轴承中心的间隙矢量eij可表示为：

间隙矢量的大小可表示为：

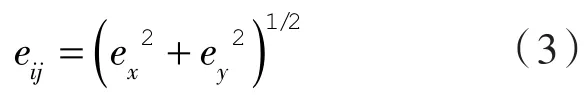
式中 ex，ey——轴承中心到曲柄销中心距离在X和Y方向的分量。

曲柄销与驱动轴承之间的穿透深度δ为：

2.2 运动副间隙的接触碰撞力模型

接触碰撞模型将碰撞过程归结为“自由运动-接触变形”两种状态的随机变换，通过考虑接触表面的阻尼和弹性因素，比较真实地描述了碰撞过程。本文采用的是一种间隙非线性连续接触碰撞力模型［9］，是基于 Lankarani-Nikravesh 接触模型与弹性模型的融合。其表达式为：

式中 Fn——接触碰撞力；

K——非线性刚度系数；

δ——接触点的法向穿透距离；

n——幂指数，取决于碰撞材料的种类，一般金属材料为1.5；

C——阻尼系数；

E*——接触表面的弹性模量；

μi，μj——2 种材料的泊松比；

Ei，Ej——2种材料的杨氏模量；

Cr——恢复系数，代表能量耗散，其值小于1，为碰撞前后的速度之比。

2.3 运动副间隙的摩擦力模型

为了进一步真实地描述运动副间隙，必须考虑接触时的切向摩擦力，采用修正的库仑摩擦模型［9］，切向摩擦力在可以表示为：

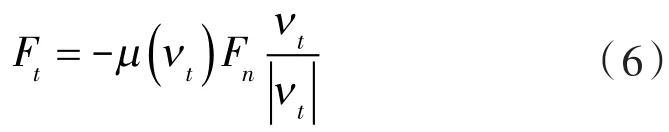
式中 vt——接触点相对滑移速度的切向分量。

此模型中的摩擦因数并不是一个常数，而是一个关于切向滑移速度的动态摩擦函数，表达式为：

式中 vs——静摩擦临界速度；

vd——最大动摩擦临界速度；

μd——动摩擦系数；

μs——静摩擦系数。

2.4 ADAMS接触碰撞力函数

ADAMS软件内置的接触碰撞力函数是IMPACT函数，其采用非线性弹簧阻尼器来计算接触碰撞力，IMPACT接触碰撞力的计算公式为：

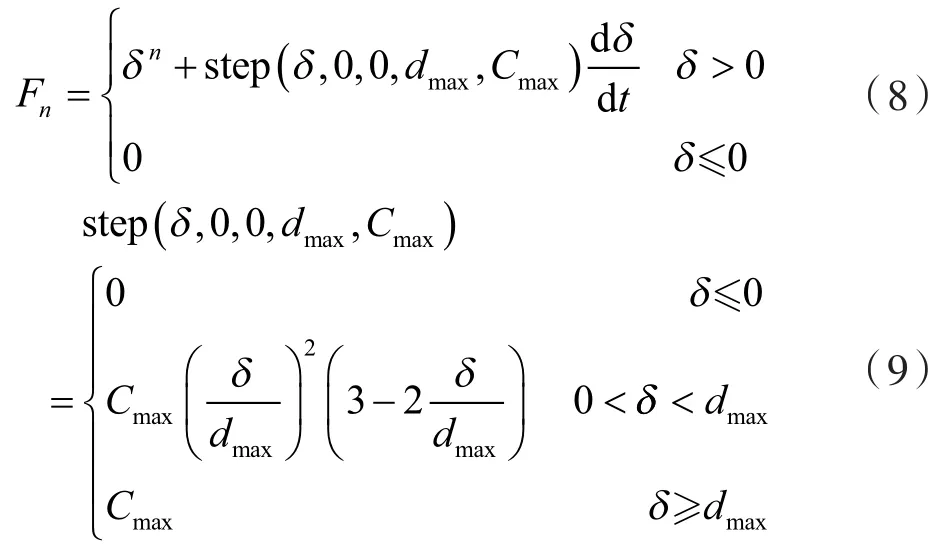
Cmax——最大阻尼系数；

dmax——在最大阻尼系数前提下的穿透边界深度。

3 涡旋压缩机转子系统动力学分析

3.1 建立转子系统动力学模型

根据表1，2所示的转子系统参数，通过SOLIDWORKS建立涡旋压缩机转子系统三维模型，驱动轴承材料为GCr15，密度为7.83 g/mm3，弹性模量219 GPa，泊松比为0.3。其型号为IS4215，外径62 mm，内径50 mm，滚针个数为55，滚针直径3.5 mm，长度为26.25 mm。然后导入ADAMS软件中建立动力学模型，模型如图3所示。

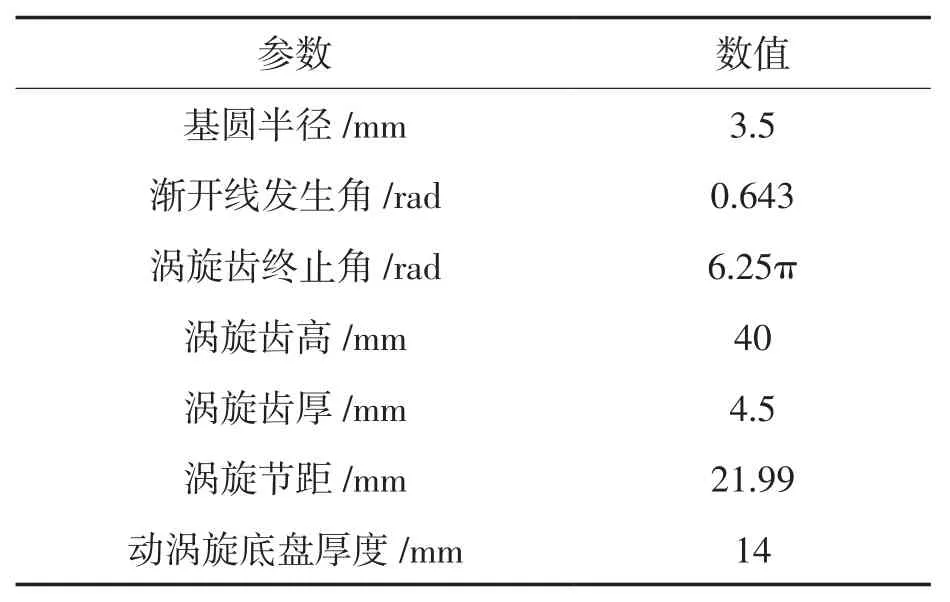
表1 型线及涡旋盘参数Tab.1 Profile and parameters of scroll member

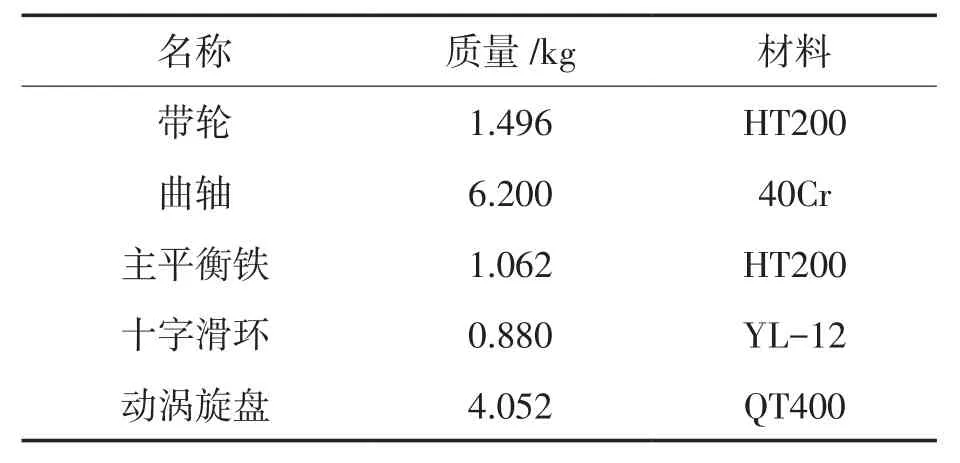
表2 转子系统各部件参数Tab.2 Parameters of each component of the rotor system

图3 转子系统动力学模型Fig.3 Dynamic model of rotor system

3.2 施加载荷及约束

根据运动副间隙对涡旋压缩机动平衡的影响，所建立的模型中曲柄销和驱动轴承连接处采用接触副连接，同时设置库仑摩擦力参数。根据转子的真实运动情况在VIEW中对各个部件施加约束以及旋转驱动并设置相应的转速函数。

3.3 动力学仿真结果与分析

由于曲轴与驱动轴承之间存在间隙，两者之间存在碰撞，引起转子系统的非理想状态运行，因此针对驱动轴承和曲轴进行测量。设置4个间隙梯度，分别为0（理想间隙），0.01，0.03，0.05 mm。

图4（a）（b）分别示出了曲轴的质心轨迹及局部放大，由图可知理想情况下曲轴的轨迹为一标准圆形，当存在间隙时质心轨迹出现了折点，而且间隙越大同一个轨迹中折点之间的距离会相应增加，曲轴的质心轨迹相对于理想情况的偏移越大。

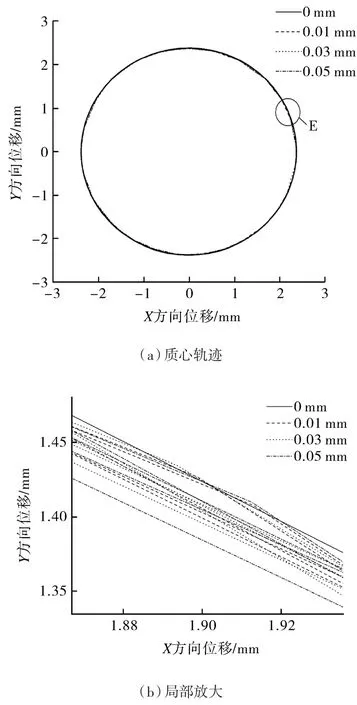
图4 曲轴位移Fig.4 Crankshaft displacement

图5（a）（b）分别示出了驱动轴承分别在水平与垂直方向上的速度变化规律，理想情况时速度曲线为光滑的正余弦曲线，存在间隙时速度曲线沿着理想情况下的曲线上下波动，随着间隙的增加速度曲线波动的峰值增大，但波动频率减小。

图6所示（a）（b）分别示出了驱动轴承在水平与垂直方向上的加速度变化，间隙为0时加速度曲线为正余弦曲线，间隙情况下的曲线沿着理想情况曲线上下剧烈的波动，并且曲线峰值随着间隙的增加而增大。

图5 驱动轴承速度Fig.5 Driving bearing velocity

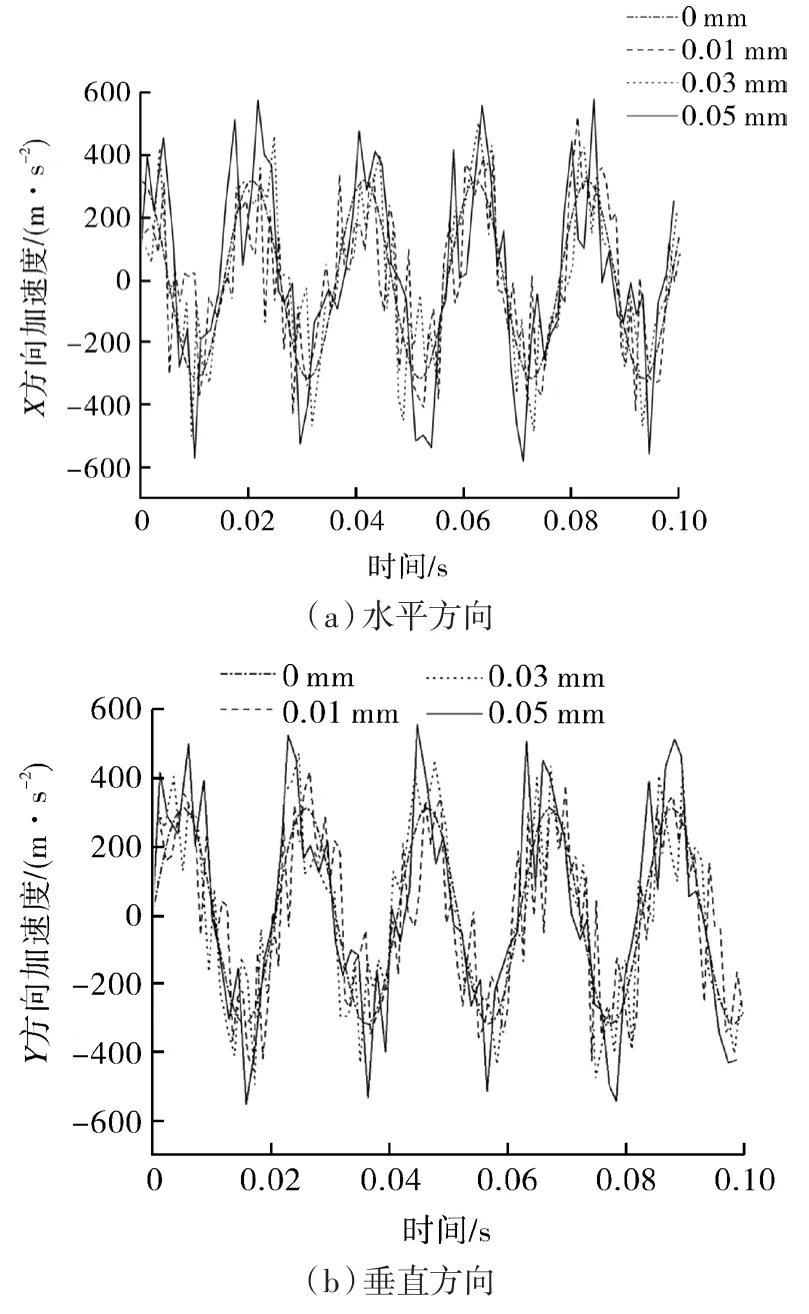
图6 驱动轴承加速度Fig.6 Driving bearing acceleration

图7示出了运动副间隙处的接触力随时间的变化规律，理想情况下接触力约为2 200 N，间隙条件下的接触力出现了高频率的波动，随着间隙的增大，接触力的瞬时峰值也逐渐增大，间隙值为0.05 mm时，曲轴与驱动轴承之间的接触力最大可达8 000 N左右，随着转动周期的增加，接触力逐渐减小并在4 000 N的范围内上下波动。

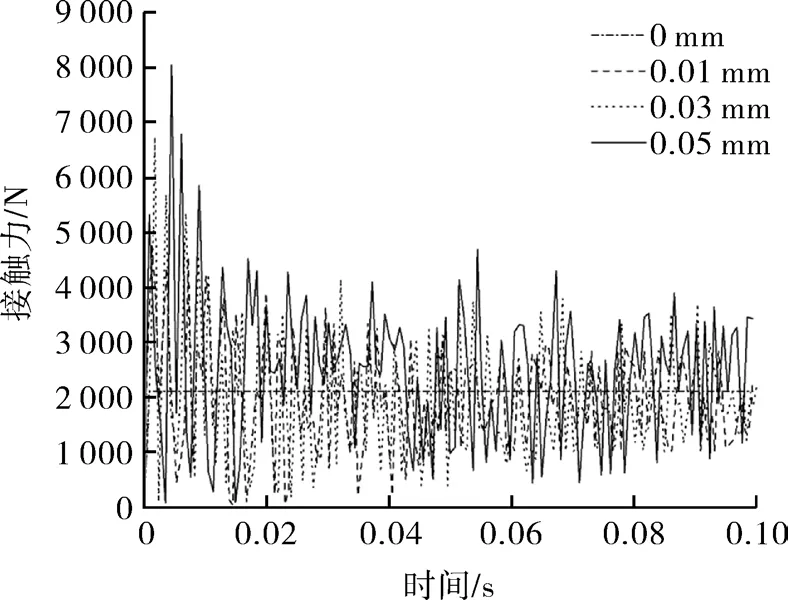
图7 曲柄销与驱动轴承之间的接触力Fig.7 Contact force between crank pin and driving bearing

从图8可知，不含间隙时驱动轴承角速度约为303 rad/s，第一个转动周期内，角速度呈现大幅度的波动，在间隙值为0.05 mm时，最大值约为304.4 rad/s，随后波动峰值逐渐减小，并沿着303 rad/s上下波动。

图8 驱动轴承角速度Fig.8 Driving bearing angular velocity

图9示出了驱动轴承角加速度随时间的变化，理想情况下驱动轴承角加速度为零，间隙的存在对角加速度的影响十分敏感，角加速度的变化十分剧烈且瞬时峰值较大。在间隙值为0.05 mm时，稳定后的角加速度在3500 rad/s2内波动。

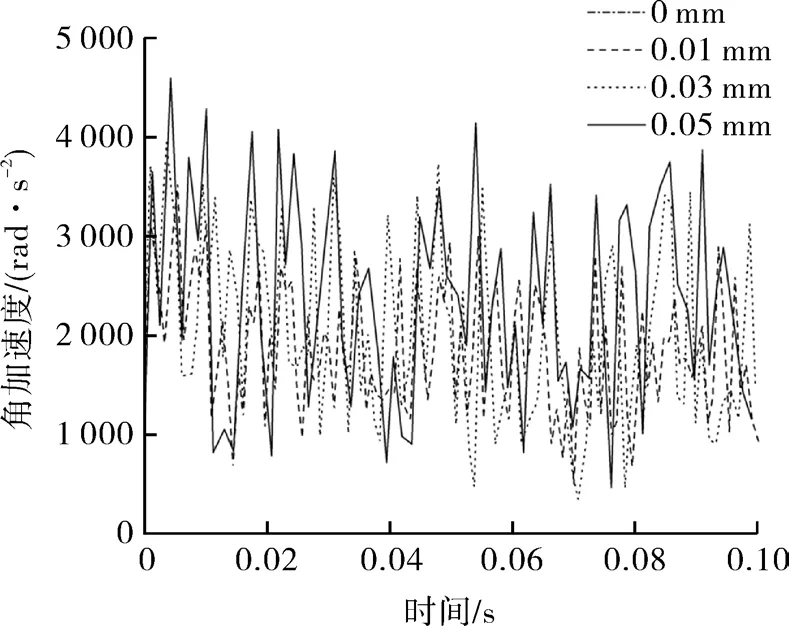
图9 驱动轴承角加速度Fig.9 Angular acceleration of driving bearing

间隙接触力、位移、速度、加速度、角速度以及角加速度的值均会随着间隙的增加而增大，但其波动的频率均会随着间隙的增加而减小。这是由于间隙增加时，驱动轴承与曲轴之间从接触状态到自由运动状态的时间也相应地增加，接触力变化的频率也就越小，但接触力的大小将变大，而力的增大导致了速度、加速度、角速度和角加速度等也随之增大。速度增大将导致曲轴与驱动轴承再次接触碰撞前构件动能增加，碰撞力增大；加速度越大，相同时间内构件速度的增速就越大，曲轴与驱动轴承再次碰撞时的碰撞力就越大；该过程是连续交替循环的，会形成恶性循环，使构件之间的磨损加剧，间隙再次增大，因此，需要对涡旋压缩机进行动平衡以控制间隙处于合理的范围，以防降低涡旋压缩机的效率甚至失效。

4 涡旋压缩机转子系统瞬态特性分析

瞬态动力学分析是对随时间任意变化的载荷作用下，结构动力响应过程的分析，动力学通用方程如下：

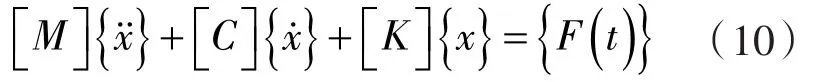
式中［M］——质量矩阵；

［C］——阻尼矩阵；

［K］——刚度矩阵；

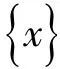
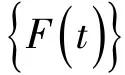
4.1 转子系统有限元模型建立

将转子系统三维模型导入到软件中，进行材料属性的定义，然后选择合适的网格进行划分，得到371 470个节点以及83 767个单元，如图10所示。

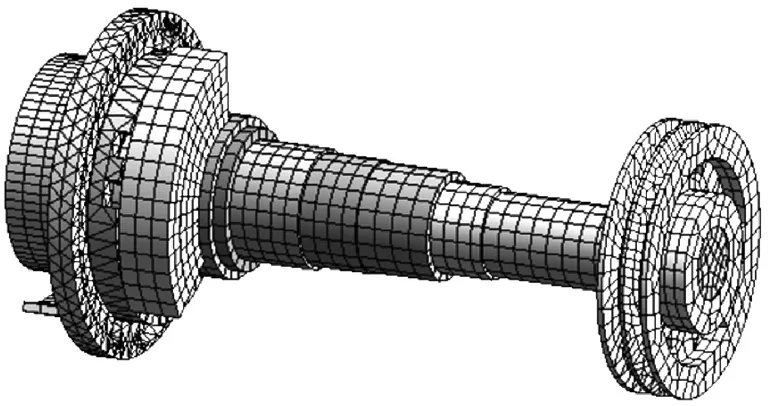
图10 转子系统网格划分Fig.10 Mesh division of the rotor system

4.2 施加载荷及约束

根据转子系统的运动特点，选择合理的载荷及约束是模拟的必要条件。首先，由于主、副轴承起支撑作用，本文采用轴承单元进行代替，如图11所示。

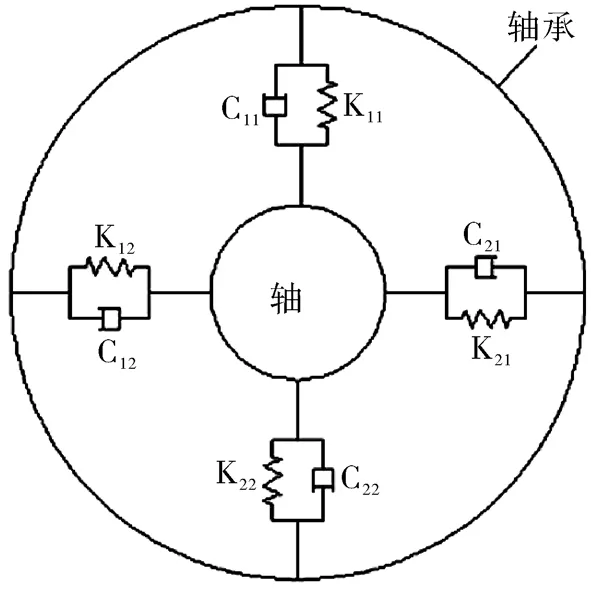
图11 轴承单元简化Fig.11 Simplified diagram of bearing unit

曲柄销处施加远端约束，曲轴尾端带轮处施加柱面约束，均限制轴向位移。然后在曲柄销处设置角加速度约束，并将获得的驱动轴承角加速度数据输入，以此作为瞬态分析的边界条件对曲轴进行分析；设置转速范围，输入不同的间隙下的刚度系数，以此对曲轴进行临界转速计算分析。

4.3 有限元仿真结果与分析

通过WORKBENCH软件计算分析可获得不同间隙值下应力分布情况，如图12所示。

在曲轴与动涡旋盘连接的曲拐处、曲轴与带轮连接的轴肩位置均发生了应力集中现象，并且曲轴与动涡旋盘连接的曲拐处的应力最大，这是因为曲柄销与主轴连接处轴径突变和曲柄销偏心导致曲柄销旋转离心力增加而引起应力集中。图12（a）所示，间隙为0.01 mm时曲轴的等效应力为25.3 MPa；图12（b）所示，间隙为0.03 mm时曲轴的等效应力为30.6 MPa；图12（c）所示，间隙为0.05 mm时曲轴的等效应力为36.4 MPa。随着间隙的增大，发生应力集中部位的应力也相应增大，这是因为不同间隙下曲轴与驱动轴承之间的接触力载荷发生了变化，接触力的大小随间隙增大而增大，使应力集中现象更加严重，而且曲轴的受力过程是连续交替循环的，这会给曲轴的安全运行带来更大的隐患。

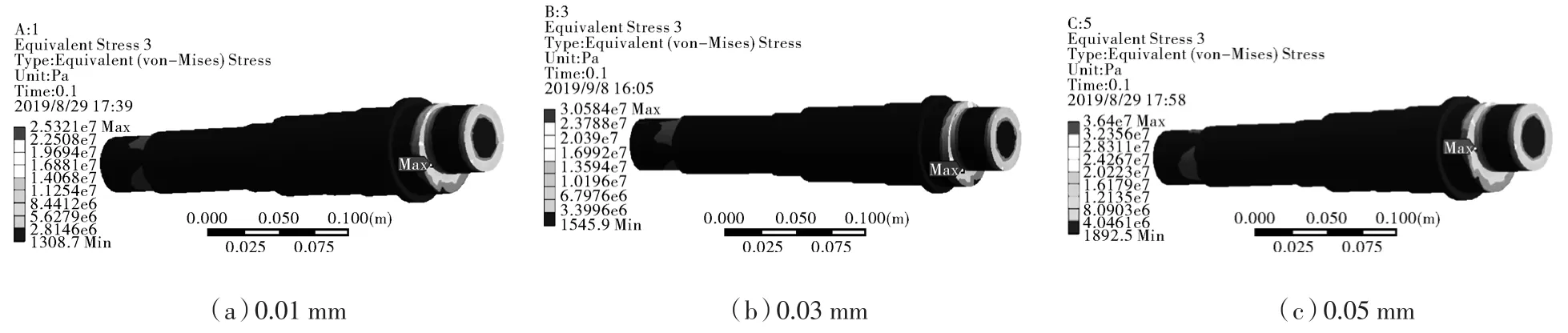
图12 不同间隙下曲轴应力分布云图Fig.12 Crankshaft stress distribution nephogram with different clearances

间隙为 0.01，0.03，0.05 mm 时，曲柄销与驱动轴承的接触刚度分别为：2.90×107，2.08×107，1.35×107N/m。经过WORKBENCH软件计算分析可画出不同间隙下曲轴系统的坎贝尔图，如图13所示分别为0.01，0.03，0.05 mm间隙时曲轴的坎贝尔图，图中的三角形分别表示不同间隙下曲轴系统的临界转速，由图可知同一间隙下该曲轴有2个临界转速，而不同间隙情况下的第一阶临界转速均小于9.13 rad/s，对应的第二阶临界转速分别为 1 447.4，1 444.3，1 438.6 rad/s。

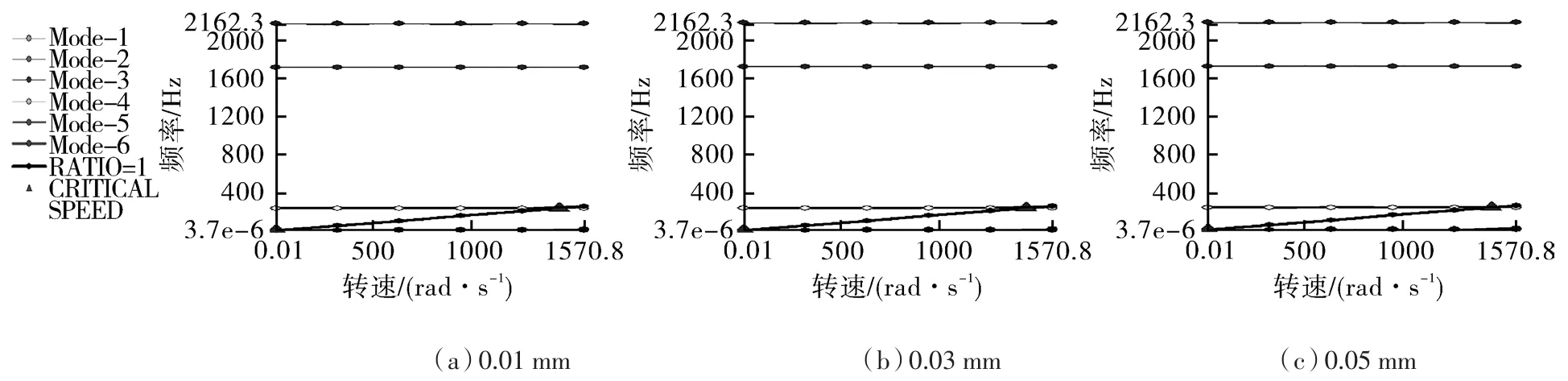
图13 不同间隙下曲轴坎贝尔图Fig.13 Campbell diagram of crankshaft with different clearances

为了保证转子正常运行，需要使转子工作转速避开临界转速，其安全裕度一般为10%～20%以上。结合图可知，由于第1个临界转速很小，转子可以很快跨跃，不会产生共振，对于第2个临界转速而言，间隙小于0.05 mm时，第2个临界转速为1 450 rad/s（约为13 800 r/min），远大于涡旋压缩机正常运行转速范围2 500～4 000 r/min，因此此种情形下也不会引起共振现象。然而当涡旋压缩机向高转速发展时，就必须考虑间隙对该临界转速的影响，否则转速越大，间隙越大时，越接近该临界转速，转子发生共振的可能性就越大，图14所示为曲轴的临界转速随间隙大小的变化情况。

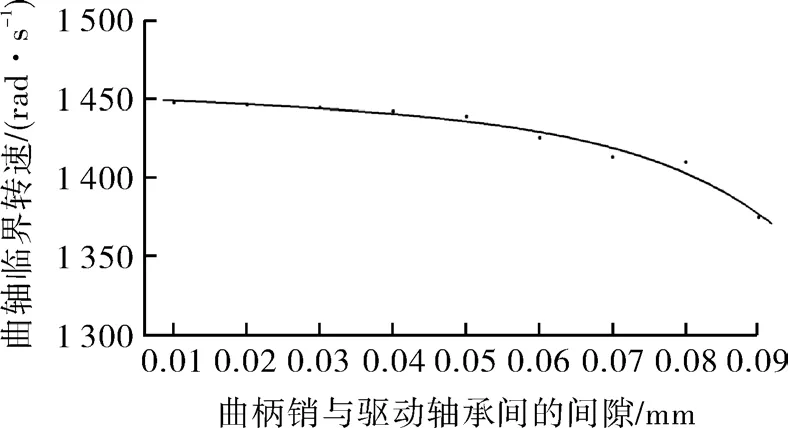
图14 不同间隙下曲轴临界转速Fig.14 Crankshaft critical speed with different clearances

由图可知，当间隙小于0.05 mm时，随着间隙的增大，曲轴系统的临界转速随之缓慢降低，是因为间隙的存在破坏了曲柄销与驱动轴承的接触刚度并使其发生变化，接触刚度随间隙的增大而减小，从而使曲轴系统的临界转速随之变小。当间隙大于0.05 mm时，曲轴临界转速随着间隙增大降低越快，极大地增加了涡旋压缩机发生共振的可能性，需要通过严格控制间隙大小和施加预紧力等措施以增加接触刚度，以避免转子共振现象。