基于T-S模型的半车辆悬挂系统控制研究
2021-02-23石广田崔彦良
石 蕊,石广田*,崔彦良
(兰州交通大学 机电工程学院,兰州 730070)
悬挂系统在车辆中扮演着越来越重要的角色,为提高车辆悬挂系统在乘坐舒适性和悬挂挠度约束等方面的性能,已做了大量研究.由于车辆主悬挂系统[1-6]簧上质量和簧下质量在载荷条件下会变化[7-8],若控制设计过程中未考虑车辆质量变化,则会影响系统性能.已提出改善悬挂系统约束性能的方法较多,如线性优化控制[9-10],T-S模糊模型[11-14]和采样控制[15-16]等.因车辆运行过程中乘客数量变化,组件损坏和通信延迟会对系统造成干扰,不确定性和时滞等问题,进而导致系统不稳定甚至性能恶化.同时,在车辆悬挂系统模型引入了非线性项.为了便于后续计算,首先必须线性化,但目前线性化的方法有微分几何理论和Taylor展开等方法,都存在一定缺陷,如微分几何理论要求被控对象模型完全精确已知,Taylor展开法仅在工作点附近才能取得较好效果.因此采用T-S模型[17-18]进行线性化,通过提出新的采样数据控制方案,将随机T-S主悬挂系统转换为连续时滞系统,基于李亚普诺夫稳定性理论设计采样状态反馈控制器便于研究随机T-S悬挂系统,确保改善悬挂性能并满足约束,使系统随机均方稳定.
1 系统描述
将静力平衡位置zc作为车身质心位移和角位移的原点,基于牛顿第二定律建立图1所示的半车辆悬挂模型的运动方程,其动力方程可描述为[19]:
(1)
(2)
(3)
(4)
悬挂挠度和轮胎载荷的硬约束可以定义为二次
控制输出,即
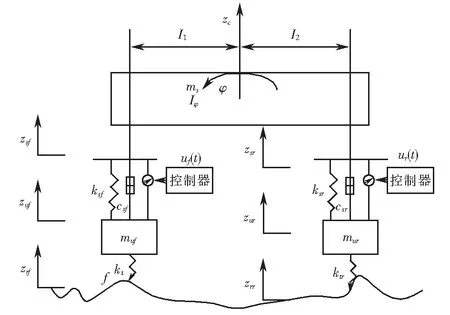
图1 半车辆模型Fig.1 Semi-vehicle suspension model
综上所述,用以下方程描述半车辆悬挂开环系统:
(5)
其中,定义增广状态向量x(t)=[x1(t)x2(t)x3(t)
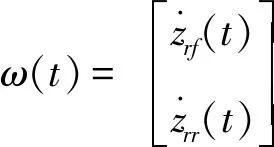
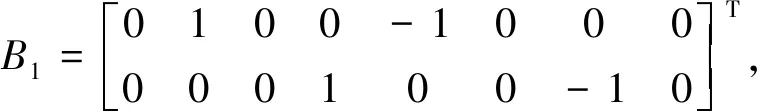
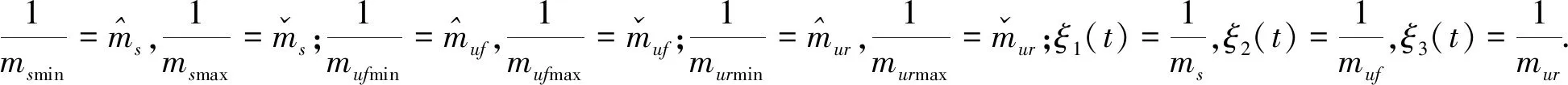
M1(ξ1(t))+M2(ξ1(t))=1,
N1(ξ2(t))+N2(ξ2(t))=1,
O1(ξ3(t))+O2(ξ3(t))=1.
计算得到以下隶属度函数:
因此,可以将系统 (5) 通过T-S模糊模型表示为如下系统[20]:
模型规则1:如果ξ1(t)是重的,ξ2(t)是重的,并且ξ3(t)是重的,则:
(6)
模型规则2:如果ξ1(t)是轻的,ξ2(t)是轻的,并且ξ3(t)是轻的,则:
(7)
模型规则3:如果ξ1(t)是轻的,ξ2(t)是重的,并且ξ3(t)是重的,则:
(8)
模型规则4:如果ξ1(t)是重的,ξ2(t)是轻的,并且ξ3(t)是轻的,则:
(9)
总之,通过模糊混合,以上系统可以表示为如下形式:
(10)
其中:
h1(ξ(t))=M1(ξ1(t))×N1(ξ2(t))×O1(ξ3(t)),
h2(ξ(t))=M2(ξ1(t))×N2(ξ2(t))×O2(ξ3(t)),
h3(ξ(t))=M2(ξ1(t))×N1(ξ2(t))×O1(ξ3(t)),
h4(ξ(t))=M1(ξ1(t))×N2(ξ2(t))×O2(ξ3(t)).
显而易见,模糊隶属度函数应满足以下条件:
考虑到在复杂运行环境和长时间工作中的悬挂系统会有一些故障存在,为了处理它在整个过程中存在的问题,故障模型可以表示为:
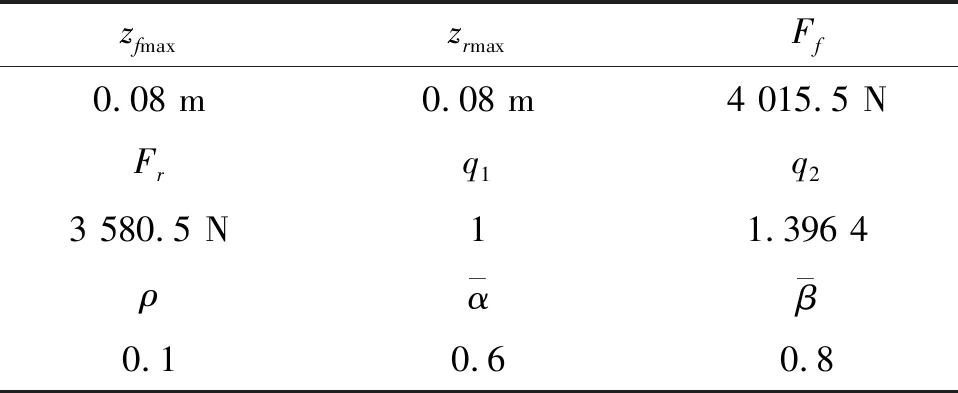
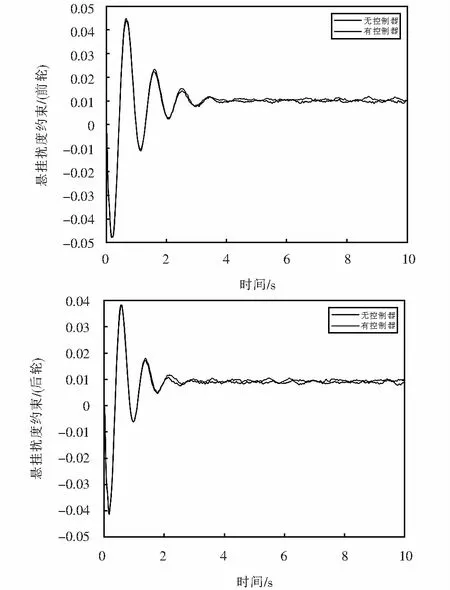
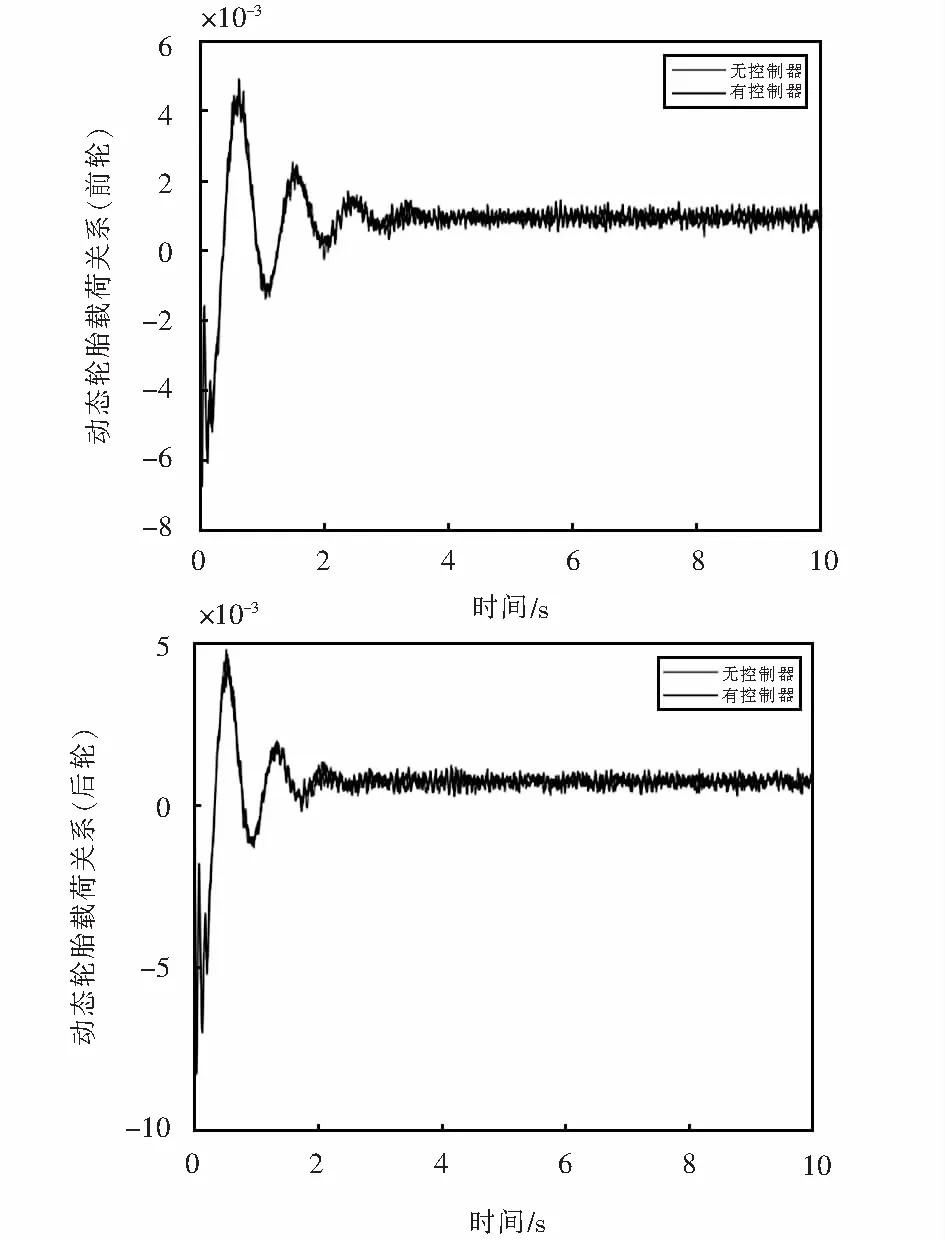
j=1,2,3,4.0≤τ1(τ) 在实际应用中,悬挂系统中通常会存在状态时滞,这将会导致系统控制性能的恶化,另一方面,由于复杂的工作环境和传输路线,对悬挂系统会产生数据包丢失的现象是不可避免的.因此,将引入两个独立的伯努利随机分布过程来描述以上问题: (t-τ2(t)), 注释:在网络环境中考虑到数据传输通道带宽限制下两个网络诱导现象是不可避免的,即随机状态时滞和数据丢失. 1) 如果α(t)=1,则传输信号只受制于时滞τ1(t);其中当τ1(t)=0时,传输信号是正常的;当0≤τ1(t) 2) 如果α(t)=0,β(t)=1时,则传输信号只受制于τ2(t),其中c1≤τ2(t) 3) 如果α(t)=0,β(t)=0时,则传输信号完全丢失. 模糊状态反馈控制器设计如下: 其中:tk=t-dk(t). 综合以上,可推导出随机T-S模糊悬挂系统的模型如下: (11) (12) (13) 存在以下表达式: 在车辆悬挂控制系统中,乘坐舒适性和操作安全性是必须处理的两个重要目标,因此,应满足以下条件[21-22]: E{‖z1(t)‖2}≤γ‖ω(t)‖2. 1) 乘坐舒适性:乘坐舒适性可以量化为车体加速度. 2) 悬挂扰度约束:为了避免损坏车辆部件和有更多乘客的不适,主动悬挂控制器必须能够防止悬挂系统达到其运行极限.因此,必须确保以下悬挂挠度: |zsf(t)-zuf(t)|≤zfmax,|zsr(t)-zur(t)|≤zrmax. 3) 轮胎与地面的附着力:为了确保轮胎与地面之间不间断接触,对前后轮胎来说,动态轮胎负荷不应超过静态轮胎负荷,即 |ksf(zuf(t)-zrf(t))|≤Ff,|ksr(zur(t)-zrr(t))|≤Fr. 对任意正定矩阵R,标量γ>0,定义向量函数f∶[0γ]→Rn的积分,即存在以下不等式[20]: Ω= (14) (15) 证明: dsdθ, 对以上所构造的李亚普诺夫函数沿系统 (11) 的轨迹进行求导可得: 利用引理1得到以下不等式: 定义任意合适矩阵S,W,U,V,利用牛顿莱布尼茨公式[23]可得: 由于Ω<0,因此 (16) 其中: D1iKjFx(t), 综合以上过程,可得以下矩阵Ω1: 可得矩阵Ω<0,以确保系统(11)随机均方稳定. ω(t)dt<0,然后整理该式可得到:E{‖z1(t)‖2}≤γ‖ω(t)‖2,因此,可以确保悬挂系统在乘坐舒适性和操作安全性方面的约束. 另一方面, 考虑控制输出z2(t): 利用数值仿真实例验证所设计控制器的有效性和可用性,半车辆模型参数在表1和表2中列出. 表1 半车辆模型参数 表2 控制器设计过程中常数选择的值 假设簧上质量的范围为ms∈[621 kg,759 kg],前后簧下质量的范围分别为mur∈[44.55 kg,45.45 kg],muf∈[39.6 kg,40.4 kg]并且故障矩阵: F=diag{0.1,0.9,0.8,0.5,0.2,0.4,0.3,0.6}. 在定理中,为了解决标准(14)(15),通过利用MATLAB线性矩阵工具箱可得到控制器增益如下: 图2和图3分别绘制了在控制律下闭环系统与开环系统的前后车体悬挂扰度约束,前后车轮动态行程约束的响应图.由图2可知所提出的方法可确保悬挂扰度约束小于0.08 m,同时,从图3可以看出,满足前后车轮动态行程约束.因此,从图2和图3可以看出通过所设计的控制器确保了系统随机均方稳定性,同时提高了系统性能,进而改善了乘坐舒适度. 图2 前后车体悬挂扰度约束的响应Fig.2 Response of front and rear body suspension deflection constraint 图3 前轮和后轮动态行程约束的响应Fig.3 Response of front and rear tire dynamic route constraint 本文研究表明,基于T-S模糊模型的振动控制策略可有效处理不确定性和信号测量丢失的半车辆悬挂系统的随机均方稳定和约束性能问题,并具有一定有效性和可行性.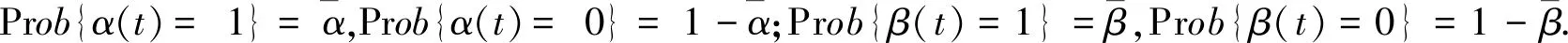
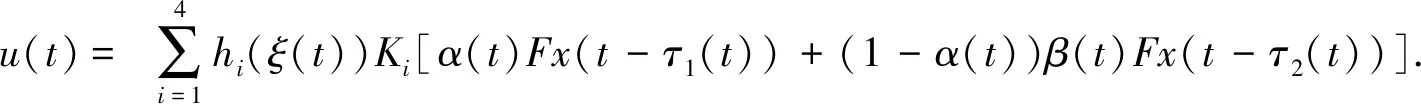
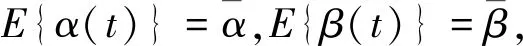
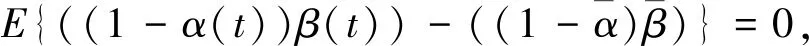
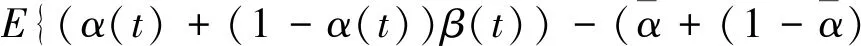
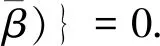
2 车辆悬挂系统的控制目标
3 主要结果
3.1 引理
3.2 定理

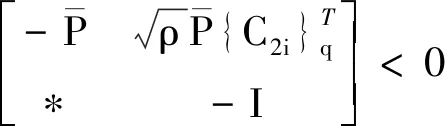
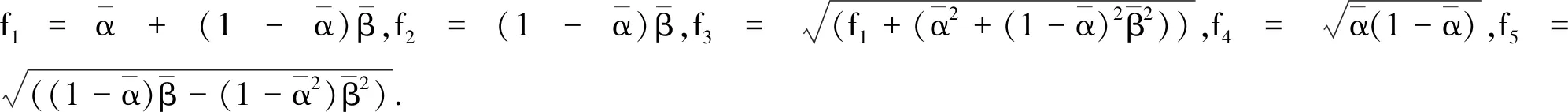
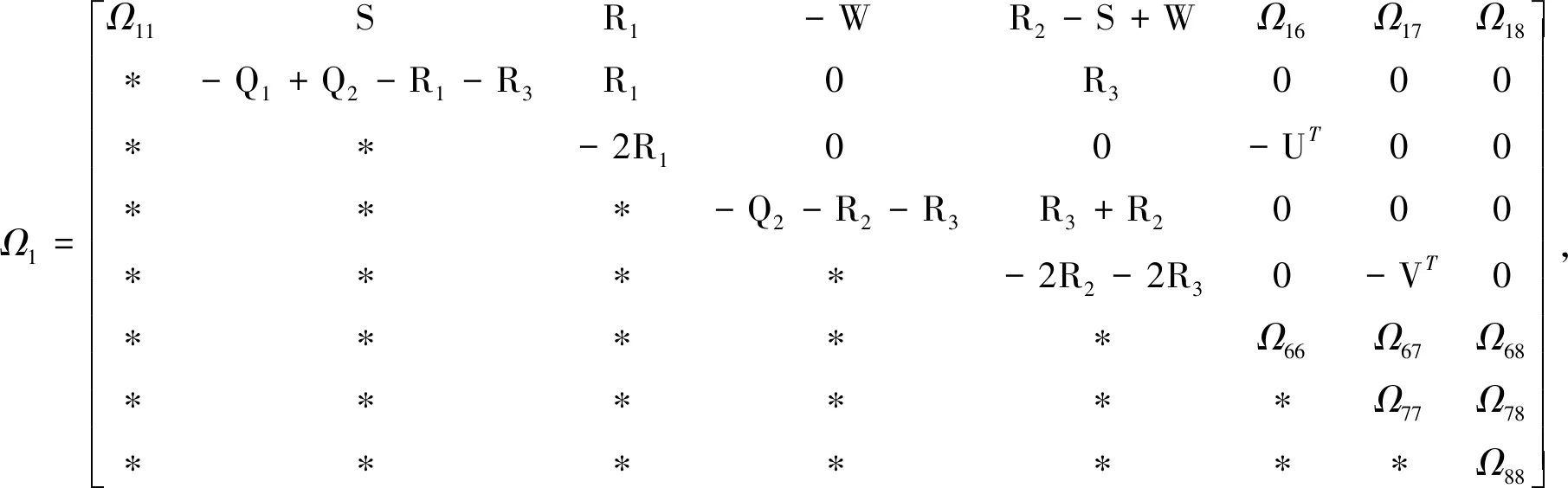
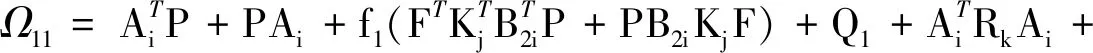
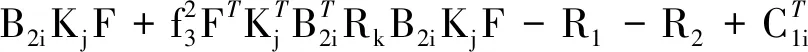
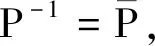

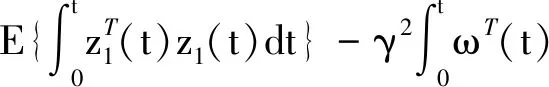
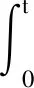
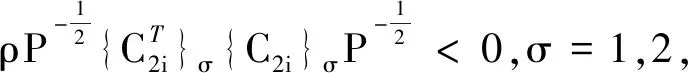
4 数值仿真

5 结论
