NOTES ON REAL INTERPOLATION OF OPERATOR Lp-SPACES*

Marius JUNGE

Department of Mathematics, University of Illinois, Urbana, IL 61801, USA E-mail: junge@math.uiuc.edu

Quanhua XU†

Institute for Advanced Study in Mathematics, Harbin Institute of Technology, Harbin 150001, China;Laboratoire de Math´ematiques, Universit´e de Bourgogne Franche-Comt´e, 25030 Besan¸con Cedex,France E-mail: qxu@univ-fcomte.fr

Abstract Let M be a semifinite von Neumann algebra. We equip the associated noncommutative Lp-spaces with their natural operator space structure introduced by Pisier via complex interpolation. On the other hand, for 1 ＜p ＜∞let

Key words operator spaces; Lp-spaces; real interpolation; column Hilbertian spaces

1 Introduction

for any compatible pair (E0, E1) of Banach spaces.

The present note concerns interpolation theory in the category of operator spaces. We refer to [2, 10] for operator space theory. The complex and real interpolations for operator spaces are developed in [8] and [13], respectively. Unless explicitly stated otherwise, all (commutative and noncommutative) Lp-spaces in the sequel are equipped with their natural operator space structure as defined in [9, 10]. Pisier proved that (1.1) and (1.3) remain true in the category of operator spaces, that is, these equalities hold completely isometrically, (E0, E1) being, of course, assumed to be operator spaces in the case of (1.3).

It is more natural to work with noncommutative Lp-spaces in the category of operator spaces. Let M be a semifinite von Neumann algebra equipped with a normal semifinite faithful trace τ. Let Lp(M) denote the associated noncommutative Lp-space (cf. [11]). If M= B(ℓ2)with the usual trace, Lp(M) is the Schatten p-class Sp. If M is hyperfinite, Pisier [9] also introduced the vector-valued Lp(M;E)for an operator space E,and showed that(1.3)continues to hold in this more general setting:

Theorem 1.1 Let 1 ＜p ＜∞with p /= 2. Then Lp,p(M) = Lp(M) completely isomorphically if and only if M is finite dimensional.

Consequently, the answers to all three Problems 6.1, 6.2 and 6.4 of [13] are negative. In particular, neither (1.2) nor (1.4) holds in the category of operator spaces.

The next theorem provides an even worse answer to Problem 6.4. It shows that(1.5)extends to real interpolation at the Banach space level only in the commutative case. Recall that one can define Lp(M;ℓq) for any von Neumann algebra M (see section 3 for more information).Lp(M;ℓq) coincides with Pisier’s space when M is hyperfinite. Note that Lp(M;ℓq) is defined only as a Banach space if M is not hyperfinite.

Theorem 1.2 Let 1 ＜p ＜∞and 1 ≤q ≤∞with p/=q. Then

The previous theorems will be respectively proved in the next three sections.

2 Proof of Theorem 1.1

We will need some preparations on column and row Hilbertian operator spaces. Let Cp(resp. Rp) denote the first column (resp. row) subspace of Spconsisting of matrices whose all entries but those in the first column (resp. row) vanish. We have the following completely isometric identifications:

where p′denotes the conjugate index of p. Cpand Rpcan be also defined via complex interpolation from C =C∞and R=R∞. We view (C,R) as a compatible pair by identifying both of them with ℓ2(at the Banach space level), i.e., by identifying the canonical bases (ek,1) of Cpand (e1,k) of Rpwith (ek) of ℓ2. Then we have the following completely isometric equalities

We refer to [8, 9] for more details.

Let Radpbe the closed subspace spanned by the Rademacher sequence (εn) in Lp([0, 1]).Then the noncommutative Khintchine inequality can be reformulated in terms of column and row spaces (see [6, 9]). To this end, we introduce

Lemma 2.1 Let 1 ＜p ＜∞. Then Radp= CRpcompletely isomorphically. Moreover,the orthogonal projection from L2([0, 1])onto Rad2extends to a completely bounded projection from Lp([0, 1]) onto Radp. All relevant constants depend only on p.

If E is an operator space, Cp(E) (resp. Rp(E)) denotes the first column (resp. row)subspace of the E-valued Schatten class Sp(E). It is clear that Cp(E)and Rp(E)are completely 1-complemented in Sp(E). Consequently, applying (1.5) to M=B(ℓ2), we get

for q ≤2 and Cp(CRq)=Sr∩St=Srfor q ＞2 too.□

Proof of Theorem 1.1 By the type decomposition of von Neumann algebras, if M is not finite dimensional, then M contains an infinite dimensional commutative L∞(Ω,μ) as subalgebra which is moreover the image of a trace preserving normal conditional expectation.Indeed, if the type I summand of M is infinite dimensional, then M contains an infinite dimensional commutative L∞(Ω,μ). On the other hand,if the type II∞summand of M exists,then M contains B(ℓ2), so ℓ∞too. Finally, if the type II1summand of M exists, then M contains L∞([0, 1]). See [12] for the type decomposition of von Neumann algebras.

Note that if L∞(Ω,μ) is infinite dimensional, L∞(Ω,μ) contains, as subalgebra, either L∞([0, 1]) or ℓ∞. On the other hand, if Lp,p(M) = Lp(M) held for M = ℓ∞, it would do so for M = ℓn∞uniformly in n ≥1. Then by a standard approximation argument, we see that it would hold for M=L∞([0, 1]) too.

3 Proof of Theorem 1.2

We begin this proof by recalling the definition of the space Lp(M;ℓq) that is introduced in[3] for q = 1 and q = ∞(see also [4]), and in [5] for 1 ＜q ＜∞. This definition is inspired by Pisier’s description of the norm of Lp(M;ℓq) in the hyperfinite case.

A sequence (xi) in Lp(M) belongs to Lp(M;ℓ∞) if (xi) admits a factorization xi= ayib with a,b ∈L2p(M) and (yi)∈ℓ∞(L∞(M)). The norm of (xi) is then defined as

Let Dp,qdenote the diagonal subspace of Cp(ℓq) consisting of all x with xij=0 for i/=j.Lemma 3.2 Let 1 ≤p,q ≤∞. Then Dp,qis completely 1-complemented in Cp(ℓq).

Proof The proof is very simple. It suffices to note that the canonical bases of Cpand ℓqare completely 1-unconditional. A standard average argument then yields the assertion.□

We will identify an element x=(xiei,1)∈Dp,qwith the sequence (xi).

Dualizing these inclusions and using Lemma 3.2, we deduce the assertion for q =∞and q =1.The case 1 ＜q ＜∞is then completed by complex interpolation via (2.3) with the help of Lemma 3.2 again.□

Remark 3.4 The previous lemma can be proved directly by Lemma 3.1 without passing to complex interpolation.

Proof of Theorem 1.2 If M is isomorphic,as Banach space,to some commutative L∞,then M is a finite direct sum of algebras of the form L∞(Ω,μ)⊗Mn, where Mnis the n×n full matrix algebra. Then (1.6) goes back to (1.4).

Conversely, suppose that M is not isomorphic to a commutative von Neumann algebra.Our first step is to reduce the non validity of (1.6) to the special case where M = B(ℓ∞).To this end, we use the type decomposition of M. If the type I summand of M is infinite dimensional, then M contains Mnfor infinite many n’s. On the other hand, if the type II∞summand of M exists, then M contains B(ℓ2). Finally, it is well known that if the type II1summand of M exists, then M contains the hyperfinite II1factor R (cf. e.g. [7]); R is the von Neumann tensor of countable many copies of (M2, tr), where tr is the normalized trace on M2; so M again contains Mnfor infinite many n’s. Note that in all the three cases, the Mn’s contained in M are images of trace preserving normal conditional expectations (up to a normalization in the type II1case).

In summary, if M is not isomorphic to a commutative von Neumann algebra, M contains Mnfor infinite many n’s which are images of trace preserving normal conditional expectations.This shows that if (1.6) held for M, then it would do so for M = Mnfor infinite many n’s;consequently, by approximation, it would further hold for M = B(ℓ2) too. This finishes the announced reduction.

It remains to show that (1.6) fails for M=B(ℓ2). Namely, we must show

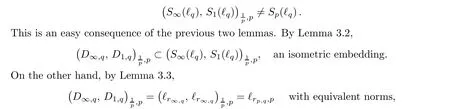
where ℓr,pdenotes the Lorentz sequence space. On the other hand, by Lemma 3.3, the corresponding subspace of Sp(ℓq) is equal to ℓrp,q. However, ℓrp,q,p= ℓrp,qif and only if rp,q= p,i.e., q =p. The theorem is thus proved.□

4 Proof of Theorem 1.3

Thus it remains to consider the case where p ≥q ≥2. This is treated by an iteration argument as above. Indeed, if q ≤4, then

It then follows that 2q≤2,which is a contradiction since q ＞1. Thus Theorem 1.3 is completely proved.