PENALIZED LEAST SQUARE IN SPARSE SETTING WITH CONVEX PENALTY AND NON GAUSSIAN ERRORS*

Doualeh ABDILLAHI-ALI Nourddine AZZAOUI Arnaud GUILLIN

Guillaume LE MAILLOUX

Laboratoire de Math´ematiques Blaise Pascal, CNRS-UMR 6620,Universit´e Clermont-Auvergne (UCA), 63000 Clermont-Ferrand, France E-mail: arnaud.guillin@uca.fr

Tomoko MATSUI

Department of Statistical Modeling, Institute of Statistical Mathematics, 10-3 Midori-cho,Tachikawa-shi, Tokyo 1908562, Japan E-mail: tmatsui@ism.ac.jp

Abstract This paper consider the penalized least squares estimators with convex penalties or regularization norms. We provide sparsity oracle inequalities for the prediction error for a general convex penalty and for the particular cases of Lasso and Group Lasso estimators in a regression setting. The main contribution is that our oracle inequalities are established for the more general case where the observations noise is issued from probability measures that satisfy a weak spectral gap (or Poincar´e) inequality instead of Gaussian distributions. We illustrate our results on a heavy tailed example and a sub Gaussian one; we especially give the explicit bounds of the oracle inequalities for these two special examples.

Key words penalized least squares; Gaussian errors; convex penalty

1 Introduction

High-dimensional statistical models have been thoroughly studied in recent research and literatures. In particular, penalized Least Square (LS) estimators have been proposed and extensively investigated;for example the ℓnorm penalized estimator LASSO and its extensions.A common feature of these estimators is the fact that the penalty is a norm satisfying some specific decomposability conditions. As shown in[5],the two main ingredients of the analysis are based on the restricted eigenvalue compatibility property, and the empirical process bounding the stochastic error. With this approach, several techniques have been proposed for a unified treatment of LS estimators with decomposable penalties, a wide overview can be found in[8, 13, 15]. Classical results were derived via oracle inequalities depending on unspecified compatibility parameters. On the other hand the penalties (and thus, the estimators) depend on the distribution with which the oracle inequality holds. To overcome these problems, a tentative for a general solution was achieved by the small ball method see for instance [10, 12].Under Gaussian noise, many results have been established for the sparsity oracle inequalities for LASSO estimators in different situations: (1) the fixed design case [1, 3-6, 8, 9] (2) results based on confidence level tied to the tuning parameter see for instance[5,6,8,9](3)in the case where the noise are i.i.d. sub-exponential. For instance, in [3, 14], sparsity oracle inequalities for the LASSO estimators are obtained in random design regression especially when all entries of the design matrix are i.i.d. standard Gaussian independent of the observations errors. In this work, we consider the classical general framework of regression model. Using the same notations as in [1, 8] it is expressed by the following:

The main result of this paper, is to derive oracle inequalities for the prediction error of the penalized estimator ˆβ (1.3) under the assumption that the noise random vector ξ in (1.1)follows a probability measure that satisfies a weak spectral gap inequality [2]. Our result is based on a compatibility constant defined as follows:

2 Statement of the Problem and Preliminary Results

Let H be a Hilbert space with inner product 〈.,.〉 and its corresponding norm ‖.‖. Let B a closed convex subset of H. We will be interested in a regression problem as in (1.1) where f ∈Ris an unknown deterministic mean and ξ ∈Ris a random noise vector. Let P be the probability distribution of ξ satisfying a weak spectral gap inequality with function γ defined in (1.2). We focus on estimates of f having the form Xˆβ where ˆβ ∈B is data determined like in (1.3). The matrix X represents a linear operator from H →R. We aim to investigate the prediction performances of the estimator ˆβ defined as the solution of the problem minimization:

where F :H →Ris a convex penalty function.

2.1 Preliminary results

2.2 Main assumptions of decomposability and compatibility

Consider the linear operator X:H →Rdefined by the relation:

Before establishing our main results, we recall two other important ingredients under which oracle inequalities are obtained namely the decomposability assumptions of the regularization norm and the compatibility factor.

3 Main Results and Oracle Inequalities

The next theorem states our main result in the case of distributions verifying the spectral gap inequality.

This achieves the proof of inequality (3.1).□

4 Application to the Classical LASSO and Group LASSO

We use the same notations as in [1]; we denote |.|for the ℓnorm of a finite dimensional vector, 1 ≤q ≤∞. The support of β will be denoted supp(β) = {j :β/=0}. If (e)is the canonical basis of R, then βwill denote the orthogonal projection of β onto the linear span of {e:j ∈S} for S ⊂{1,··· ,p}.

4.1 Application to LASSO

In this case H = B = Requipped with the Euclidean norm ‖.‖= |.|. The penalty function is given by ‖.‖ the ℓnorm. Then the estimator ˆβ defined in (2.7) is the LASSO estimator

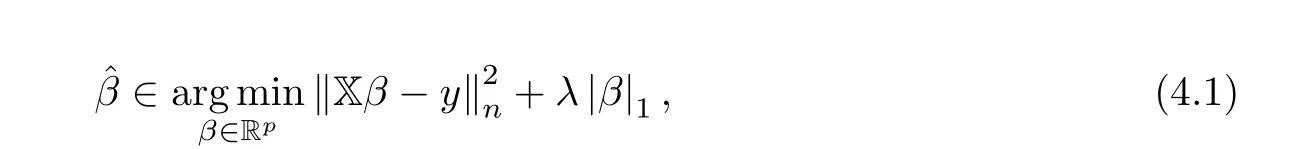
where λ ＞0 is a tuning parameter. For β ∈R,we consider the decomposability conditions with P, the orthogonal projection operator onto the linear span of {e:j ∈supp(β)}. Following a similar argument as in [1] or [3, 8], one can show, using the duality between ℓand ℓnorms,that for LASSO setting the set Ω defined in (2.3), becomes:

In the following we recall that, in the LASSO setting, the Assumption 2.1 holds for the orthogonal projection operator.

4.2 Upper bound of the compatibility factor

In this section we state a close form for the upper bound of the compatibility factor μ(β).For this purpose, we need the following results:

Lemma 4.1 In the LASSO setting, with a,τ and t verifying conditions of Theorem 3.1,we have the following:

1. For the orthogonal projector operator P, the Assumption 2.1 is satisfied.

2. The modified compatibility factor we defined in (1.4) can be expressed as follows:

In the following proposition we give, for a fixed ζ, the value of the supremum of the right hand side of inequality (4.3).

Proposition 4.2 Fix ζ ∈(0,1). For every β ∈Rsuch that|supp(β)|=|{j : β/=0}|=s for some integer 1 ≤s ≤p, we have

4.3 Application to special distributions

In this section we establish explicit oracle inequalities for the two examples of heavy tailed and sub-exponential distributions discussed bellow. In order to show the main results we need to find, for each distribution family, τ such that P(Ω)＞1/2.

Lemma 4.4 Let X be a deterministic matrix ∈R, then we have:

1. Suppose that the probability distribution P is issued from the product of (3.7). In this case if

1. By the concentration inequality[2]applied to(3.7),there exists constants t(α)＞e and C(α) such that for all t ＞t(α),

We have a similar result for the sub-exponential example that we state in the following theorem.

4.4 Application to Group LASSO in case of the heavy tailed example

In order to shorten the length of the paper, we will discuss, in this sub-section, only the case where ξ has a heavy tailed distribution issued from(3.7). A similar result can be obtained for the other sub-exponential example. We begin by introducing the notations usually adopted in literature for the group LASSO as follows: Let G,··· ,Gbe a partition of {1,··· ,p}.We denote β= (β)and, for every 1 ≤p ＜∞, we define the mixed (2,q)-norm and

Without loss of generality, we assume, in the following, that the groups Ghave the same cardinality|G|=p/M,k=1,··· ,M. Since we consider mainly sparse vectors,it is convenient to define a generalization of the support concept. To any β ∈R, let:

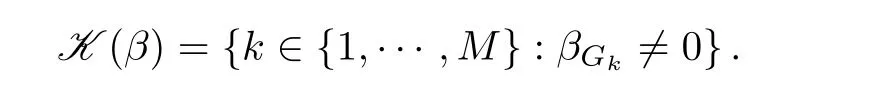
It plays the role of support by block of vector β. As for the LASSO application, we begin by verifying the decomposability assumptions and we bound the compatibility factor for the heavy tailed example introduced above.

Lemma 4.7 Consider X is a matrix ∈Rand β ∈R,

We consider now to control the compatibility μ(β) for any group sparse vector β ∈Rwhich means that |K (β)| is much smaller than M the number of groups. For this purpose, we will need the following RE(s) condition introduced in [11, Assumption 3.1].

Assumption 4.1 (RE(s) condition) For any S ⊂{1,··· ,M}, let c＞0 be a constant and 1 ≤s ≤M be an integer that gives an upper bound on the group sparsity of a vector δ,the following condition holds.

5 Conclusion

In this paper we discussed penalized least squares estimators with convex penalty or regularization norms. We focused on regression model where the observations noise are independent and follow a probability measure which satisfies a weak spectral gap(or weak Poincar´e)inequality. We established oracle inequalities in probability for the prediction error for the LASSO and Group LASSO estimators. Our results have been applied to two examples of non Gaussian cases; namely a heavy tailed and a sub-exponential examples. For these cases we explicit the oracle inequalities bounds in a close form.