HANDEL’S FIXED POINT THEOREM: A MORSE THEORETICAL POINT OF VIEW*

Abstract Michael Handel has proved in [10] a fixed point theorem for an orientation preserving homeomorphism of the open unit disk, that turned out to be an efficient tool in the study of the dynamics of surface homeomorphisms. The present article fits into a series of articles by the author [13] and by Juliana Xavier [21, 22], where proofs were given, related to the classical Brouwer Theory,instead of the Homotopical Brouwer Theory used in the original article. Like in [13, 21] and [22], we will use “free brick decompositions” but will present a more conceptual Morse theoretical argument. It is based on a new preliminary lemma, that gives a nice “condition at infinity” for our problem.

Key words brick decomposition; Brouwer theory; translation arc

1 Introduction

In this article, the unit circle S = {z ∈C||z| = 1} of the complex plane is, as usual,oriented counterclockwise and this orientation induces an orientation on every interval of S. If a and b are two distinct points of S, we denote (a,b) the open interval of S that joins a to b for the induced orientation. We will denote D = {z ∈C||z| = 1} the unit disk. Let f be a homeomorphism of D and Γ ⊂D a simple loop that does not contain any fixed point of f.Recall that the index i(f,Γ) is the degree of the map

Figure 1

This theorem is usually called Handel’s fixed point theorem. The original version(see [10])is a little bit weaker: f is supposed to extend continuously to S and the conclusion is that f has at least one fixed point. It is a highly important result in the study of the dynamics of surface homeomorphisms. For very nice applications,see Franks[7, 8]or Matsumoto[17], for instance.The proof of Handel, which is judged very tough, is based on Homotopical Brouwer Theory which is the study of the mapping class group of the complement of finitely many orbits of a Brouwer homeomorphism, meaning a fixed point free orientation preserving homeomorphism of D (see [10, 16] or [1]).

A proof of Theorem 1.1 was given in [13], based on the classical Brouwer Theory, that used only topological arguments (and no geometrical argument). The fundamental fact is that the hypothesis of the theorem implies that f is recurrent, a property known to imply the conclusion. This property will be defined very soon in the text, like all the notions we will introduce in the following lines. The proof given in [13] is a proof by contradiction. Assuming that the map is not recurrent,a preliminary lemma is proved in terms of translation arcs,giving some description of the dynamics in neighborhoods of the αiand the ωi. A maximal free brick decomposition can be constructed on the complement of the fixed point set, that “contains”the dynamical elements described in the lemma. Then it is possible to show that this brick decomposition contains a closed chain, property that implies that the map is recurrent,which contradicts the hypothesis. A simplification of the proof was obtained by Xavier in [21] and[22]. Starting with the same preliminary lemma, a different argument was used to prove the existence of a closed chain in the brick decomposition, whose main interest is that it works for a wider class of brick decompositions that the ones considered in [13]. It must be noticed that generalizations of Handel’s fixed point theorem have been stated by Xavier, replacing the“elliptic” situation expressed in Theorem 1.1 by “hyperbolic” or “degenerate” situations.

In the present article,we display a new proof of Theorem 1.1 which follows the same outline as the proofs of [13, 21] and [22]: first an introductory lemma, like in the cited articles, then a construction of a brick decomposition similar to the construction done by Xavier and then a proof of the existence of a closed chain. The introductory lemma used in the present article,slightly different from the one appearing in [13, 21] and [22], is much easier to prove. It seems weaker than the old one but curiously turns out to be more efficient for our purpose. The arguments, relative to a brick decomposition, that appear later in the proof are more conceptual than those described in [13, 21] and [22]: a Morse theoretical reasoning using a condition at infinity given by the introductory lemma. It must be pointed out that one of the nicest applications of Handel’s fixed point theorem is the extension by Matsumoto of the Arnold conjecture to Hamiltonian surface homeomorphisms, and that the classical version for diffeomorphisms(see [5] or [19]) is related to Morse theory and its extensions, like Floer homology,like so many results of symplectic topology.

The natural question being at the origin of[13]is the following: can Theorem 1.1 be directly deduced from the foliated version of Brouwer Translation Theorem? The preliminary lemma that is given here permits to answer positively to this question, at least to prove the existence of a fixed point.

Let us explain now the plan of the article. We will recall in the next section the principal results of Brouwer Theory and will define precisely the many objects introduced above. In a short Section 3 we will introduce definitions related to ordered sets that will be used throughout the text. In Section 4 we will recall classical results about brick decompositions on surfaces.The introductory lemma will be stated and proved in Section 5, and it will be used in Section 6 to construct a nice brick decomposition. The proof of Theorem 1.1 will be done in Section 7. Some supplementary comments will be done in Section 8. In particular the links with the foliated version of Brouwer Translation Theorem will be explained there. We have tried to make the article as self-contained as possible, adding precise references for the most technical details.

2 Recurrent Homeomorphisms and Brouwer Theory

Usually, Brouwer Theory concerns with homeomorphisms of C but can be translated immediately to homeomorphisms of a topological set homeomorphic to C. As we are interested in homeomorphisms of D in this article, we will state the results in D.

An open disk of a topological surface S is a subset V ⊂S homeomorphic to D. A path is a continuous map γ : I →S, where I is a non trivial real interval. Suppose that γ is injective and proper: it is a segment if I is compact, a line if I is open, and a half line if I =[a,+∞)or I =(-∞,a]. As usual, we will often identify a path and its image.

2.1 Recurrent homeomorphisms

Let S be a topological surface and f a homeomorphism of S. A subset X ⊂S is f-free if f(X)∩X =Ø (we will say simply free if there is no ambiguity). Following [13], we say that f is recurrent if there exists a family of pairwise disjoint free open disks (Vj)j∈Z/rZ, r ≥1,and a family of positive integers (kj)i∈Z/rZsuch that fki(Vj)∩Vj+1/=Ø, for every j ∈Z/rZ (such a family is usually called a closed chain of free disks of length r, see[6]). This property is clearly invariant by conjugacy. A simple example of a recurrent homeomorphism of S is given by a homeomorphism that contains a non wandering free open disk,meaning a free open disk V such that there exists k ＞0 such that fk(V)∩V /=Ø. In particular,if the set of non wandering points is larger than the fixed point set, then f is recurrent. There exist more surprising examples of recurrent homeomorphisms, like the map f : zz/2 defined on C. Indeed the segment γ :t(8π-6πt)e2iπtdefined on [0,1] is free but it holds that f2(γ)∩γ /=Ø. So, one can find a free open disk V that contains γ and one knows that f2(V)∩V /=Ø.

The fundamental property about recurrent homeomorphisms noticed by Franks in[6]is the fact that a periodic orbit can be obtained by continuous deformation,without adding any fixed point. Indeed,suppose that f is recurrent and write fix(f)for the fixed point set. One can find an integer r such that there exists a closed chain of free disks of length r but no closed chain of free disks of length ＜r. Fix such a chain (Vj)j∈Z/rZ. There exists a sequence of positive integers (kj)j∈Z/rZ, uniquely defined, such that:

2.2 Brouwer Theory

is an f-invariant open set homeomorphic to C and the map f|Wis conjugate to a non trivial translation of C. As a consequence, we know that every point z of D is wandering, meaning that there is a neighborhood U of z such that the fk(U), k ∈Z, are pairwise disjoint. The proof of Brouwer Translation Theorem uses a preliminary result, stating that if an orientation preserving homeomorphism f of D has a periodic point of period p ＞1, then there exists a simple loop Γ ⊂Dfix(f) such that i(f,Γ) = 1 and consequently f has a fixed point. In fact this preliminary result can be expressed in terms of translation arcs (see [2, 4] or [9]). A segment γ :[0,1]→D is a translation arc of f if it joins a point z /∈fix(f) to f(z) and if:

· either γ ∩f(γ)={z};

· or γ ∩f(γ)={z,f(z)} and f2(z)=z.

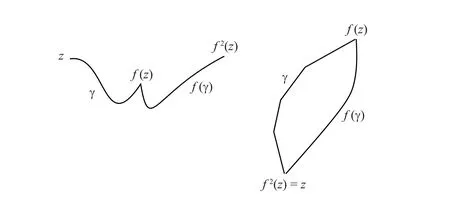
Figure 2

Proposition 2.1 Let f be an orientation preserving homeomorphism of D and γ a translation arc of f joining a point z to f(z). If γ ∩f(γ) is not reduced to f(z) or if there exists k ＞1 such that γ ∩fk(γ) /= Ø, then one can construct a simple loop Γ ⊂Dfix(f) such that i(f,Γ)=1.

It is not difficult to construct a translation arc γ passing through a given point z (we will see the construction in Section 5). If z is periodic,then γ satisfies the hypothesis of Proposition 2.1 and so, there exists a simple loop Γ ⊂Dfix(f) such that i(f,Γ)=1.

Suppose that the hypothesis of Proposition 2.1 are satisfied. If z is periodic, then one can find a free open disk V containing z, and one knows that there exists k ＞0 such that fk(V) ∩V /= Ø. If z is not periodic, there exists k ＞1 such that γ ∩fk(γ) /= Ø. Fix z′∈γ ∩f-k(γ) and denote γ′the sub-segment of γ that joins z′to fk(z′). It is different from γ because z is not periodic and consequently it is free. So, one can find a free open disk V that contains γ′and one knows that fk(V)∩V /=Ø. In all cases, there exists a non wandering free open disk and so f is recurrent.

Let us recall now the following result of Franks [6]:

Proposition 2.2 If f is an orientation preserving recurrent homeomorphism of D, then there exists a simple loop Γ ⊂Dfix(f)such that i(f,Γ)=1. Consequently,f has at least one fixed point.

Indeed,as seen in Section 2.1,there exists a continuous family(ht)t∈[0,1]of homeomorphisms such that:

· ht=Id;

· fix(ht◦f)=fix(f) for every t ∈[0,1];

· h1◦f has a periodic point of period p ＞1.

By Proposition 2.1, there exists a simple loop Γ ⊂Dfix(h1◦f) that does not contain any fixed point of h1◦f, such that i(h1◦f,Γ)=1. The integer i(ht◦f,Γ) is well defined for every t ∈[0,1], because fix(ht◦f)=fix(f) for every t ∈[0,1], and depends continuously on t. So it is independent of t, and we have i(f,Γ)=1.

Let us conclude with a characterization of the recurrence due to Guillou and Le Roux (see[15], page 39). If Σ is a submanifold of D (with or without boundary, of dimension 0, 1, or 2)we will denote ∂Σ the boundary of Σ and define int(Σ)=Σ∂Σ.

3 Ordered Sets and Cuts

We will consider different orders in the article, so let us introduce some definitions and notations that will be used later.

Let (X,≤) be an ordered set. For every x ∈B, we denote

4 Brick Decompositions

In this section, we will recall some facts about brick decompositions (see Sauzet [18] or[12]). The results of the last sub-section are the only ones which are new. Nevertheless it seems useful to include some proofs of known results to make this article as self-contained as possible.

4.1 Definitions

A brick decomposition D = (V,E,B) on an orientable surface S is defined by a locally finite graph Σ(D) of S, the skeleton of D, such that any vertex is locally the extremity of exactly three edges. Here V is the set of vertices, E the set of edges (meaning the closures in S of the connected components of Σ(D)V) and B the set of bricks (meaning the closures in S of the connected components of S Σ(D)). Note that every edge is the image of a proper topological embedding of [0,1], [0,+∞), R or S and that every brick is a surface (usually with boundary).

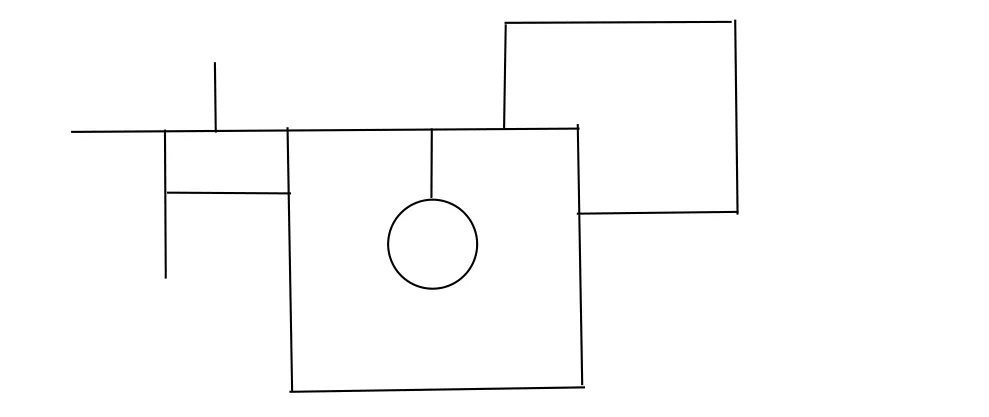
Figure 3

In fact,for every X ∈P(B),the union of bricks b ∈X is a sub-surface of S with a boundary contained in Σ(D). It is connected if and only if for every pair of bricks b,b′∈X, there exists a sequence (bj)0≤j≤nsuch that:

· b0=b and bn=b′;

· bjand bj+1are adjacent for i ∈{0,··· ,n-1} (meaning that they contain a common edge).

The maximal connected subsets of a set X ∈P(B)will be called the connected components of X.1Connected components will usually simply be called components in the text.For simplicity we will denote by the same letter a set of bricks and the union of these bricks, and will write X ⊂B or X ⊂S if specification is needed. We will say that two disjoint sets X and Y of B are adjacent if ∂X ∩∂Y /= Ø or equivalently if there is an edge e ∈E that is contained in both a brick of X and a brick of Y.

A brick decomposition D′=(V′,E′,B′) is a sub-decomposition of D if Σ(D′)⊂Σ(D). In that case V′is a subset of V, every edge in E′a union of edges in E and every brick in B′a union of bricks in B. Observe that one may have B′=B even if D′/=D.

4.2 The induced maps

4.3 Free brick decompositions, the induced order

Lemma 4.1 Let f be a non recurrent fixed point free homeomorphism of S and D =(V,E,B) be a maximal free brick decomposition of f. The following conditions are equivalent,for a given brick b ∈B:

(1) there exists b′adjacent to b such that f(b)∩b′/=Ø,(2) b≥is connected;and they imply that b＞is connected. In the case where these conditions are satisfied, we will say that b is positively regular. Otherwise we will say that b is positively singular.

Proof The inclusion (2) ⇒(1) is obvious. Indeed, b≥contains b and is it reduced to b,so it contains a brick b′adjacent to b if it is connected. Of course, f(b′)∩b=Ø because b′≥b and so we have f(b)∩b′/=Ø. To prove the inclusion (1)⇒(2), note that φ+({b}) is connected for every b ∈B and so{b}∪φ+({b})is also connected if(1)is satisfied. Consequently,each set

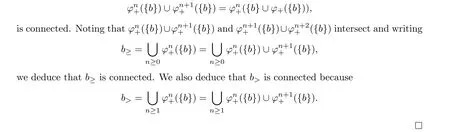
Similarly we will say that b is negatively regular if b≤is connected, meaning that there is a brick b′adjacent to b such that b′≤b. Otherwise it will be called negatively singular. We will say that b is regular if it is both positively and negatively regular and singular otherwise.

4.4 Attractors and repellers

In the case where f is a non recurrent fixed point free homeomorphism of S and D =(V,E,B)is a maximal free brick decomposition of S,then C is regular if and only if contains at least two bricks, and singular if and only if it is reduced to a positively singular brick. Indeed,let C be a component of A and denote C′the component of A containing φ+(C). If #C ≥2,then C contains two adjacent bricks and so φ+(C)∩C /=Ø. Consequently one has C′=C. If C is reduced to a brick b, then C′/= C because b is free. Moreover, C ∪C′is not connected,which implies that φ+({b}) does not contain a brick adjacent to b. So b is positively singular.

Similarly,a repeller is a set R ⊂B such that φ-(R)⊂R or equivalently such that f-1(R)⊂int(R). We have a similar classification for its components. Note also that R is a repeller if and only if BR is an attractor. In fact, a couple (R,A) such that {R,A} is a partition of B that consists of a repeller R and an attractor A, is a cut of ≤. Observe that ∂R=∂A.

4.5 New and useful results

We will finish this section by proving some new results on brick decompositions that will be useful to our purposes. We suppose that f is a non recurrent orientation preserving homeomorphism of the 2-sphere S2and that D =(V,E,B) is a maximal free brick decomposition of f|S2fix(f). We denote ≤the induced order on B and φ+, φ-the induced maps on P(B)2.

We begin with the following lemma:

Lemma 4.2 The boundary of a singular brick is a line of S2fix(f), whose closure in S2meets a unique connected component of fix(f).

Proof It is sufficient to prove the lemma for negatively singular bricks. Let b be such a brick. Its boundary is a boundaryless 1-submanifold of S2fix(f) and each of its component is

· a simple loop,

· or a line of S2fix(f) whose closure in S2meets a unique connected component K of fix(f),

· or a line of S2fix(f) whose closure in S2meets exactly two connected component Kand K+of fix(f).

Let us prove first that if there exists a component Γ of ∂b which is a line of S2fix(f)whose closure in S2meets exactly one connected component K of fix(f), then ∂b = Γ. The line Γ is contained in a component W of S2K, this component is homeomorphic to D and Γ separates W. We denote U the connected component of W Γ that contains int(b) and V the other one.The bricks b′/=b adjacent to Γ are included in V. The brick b being negatively singular, f(b)meets every brick adjacent to b. Moreover f(b) is connected and disjoint from Γ because b is free. So every brick adjacent to b is in V. This implies that ∂b has no component but Γ.

Let us prove now that no component of ∂b is a loop. We argue by contradiction and suppose that such a component Γ exists. It separates S2. We denote U the connected component of S2Γ that contains int(b) and V the other one. The same proof as above tells us that every brick adjacent to b is in V. One deduces that b = U. In this situation, the set X of bricks adjacent to b is finite. For every b′∈X,the set f-1(b′)meets b but is not included in b(because the image by f-1of an edge e ⊂b ∩b′is disjoint from b). Moreover f-1(b′) is connected and so it meets another brick of X. We have proved that for every b′∈X there exists b′′∈X such that b′′＜b′. This is not compatible with the finiteness of X.

Let us conclude by proving that the third case never occurs. We argue by contradiction and consider a component Γ of ∂b which is a line of S2fix(f)whose closure in S2Of course, by considering its extension to the Alexandrov compactification of D, everything will work for a homeomorphism f of D if we replace S2fix(f) with Dfix(f).meets exactly two connected component K-and K+of fix(f). The line Γ is contained in a component W of S2(K-∪K+), this component is homeomorphic to the annulus S×R and Γ does not separate W but joins its two ends. Consequently, Γ is not the unique component of ∂b. The brick b, being negatively singular, is positively regular and so Lemma 4.1 tells us that b ≥and b＞= b≥{b} are connected. The brick b being negatively singular, every brick adjacent to b belongs to b＞. The connectedness of b and b＞implies that b≥contains an essential simple loop Γ′, meaning non homotopic to zero in W. Its image by f is contained in the interior of b＞and consequently does not meet Γ. So it cannot be essential and we have got a contradiction. □

Corollary 4.3 Let (R,A) be a cut of ≤. If a singular component R′of R is adjacent to a component A′of A, then A′is the only component of A that is adjacent to R′.

Proof Recall that R′is reduced to a single brick,which is negatively recurrent. The sets R and A have the same boundary and every component of this boundary is the boundary of a unique component of R and of a unique component of A. By Lemma 4.2,the boundary of R′is connected. It is a connected component of the boundary of R,and so is a connected component of the boundary of a component A′of A, moreover A′is the unique component of A that is adjacent to R′.□

Of course, one proves similarly that if a singular component A′of A is adjacent to a component R′of R, then R′is the only component of R that is adjacent to A′.

Proposition 4.4 Let (R,A) be a cut of ≤. If R′is a regular component of R and A′a regular component of A and if there exists n ≥1 such that fn(R′)∩A′/= Ø, then R′and A′are adjacent.

Proof Let X be the union of R′and of the components of A that are adjacent to R′. It is a connected set and we want to prove that it contains A′. Let e be an edge included in ∂X.Denote b the brick containing e and included in X and b′the other brick. Of course b /∈R′,otherwise b′would belong to a component of A adjacent to R′and so would belong to X. So,b belongs to a connected component A′′of A that is adjacent to R′and b′is contained in a connected component of R adjacent to A′′and different from R′. By Corollary 4.3, it implies that A′′is regular and we have f(e) ⊂f(A′′) ⊂int(A′′) ⊂int(X). So, X is a connected set such that f(∂X) ⊂int(X). Moreover, if A′is not adjacent to R′, then A′∩X = Ø in B but also in S2. By hypothesis, the sequence (f-k(A′))k≥0is increasing and for k large enough it holds that f-k(A′)∩R′/= Ø. Consequently, there exists k ≥0 such that f-k(A′)∩X = Ø and f-k-1(A′)∩X /= Ø. But f-k-1(A′) is connected and not included in X. It implies that f-k-1(A′)∩∂X /=Ø, which implies that f-k(A′)∩int(X)/=Ø. We have found a contradiction.

□

5 A Preliminary Lemma

Figure 4

Figure 5

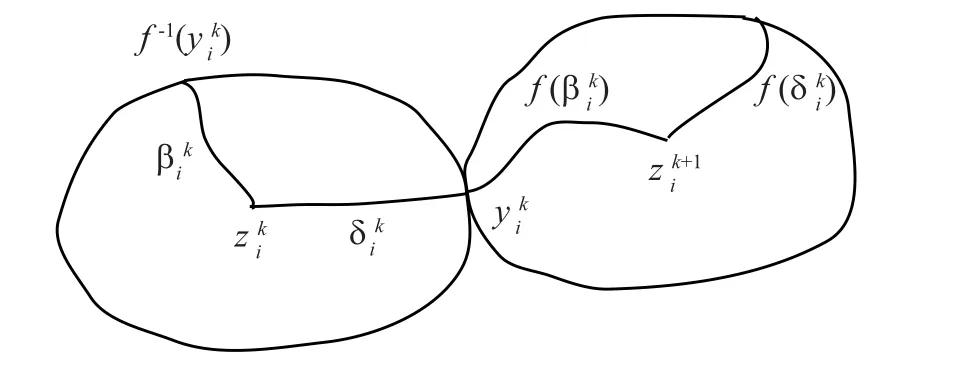
Figure 6

6 An Adapted Brick Decomposition

6.1 Construction of critical graphs

Figure 7

6.2 Construction of an adapted brick decomposition

Figure 8

7 Proof of Theorem 1.1

We consider the brick decomposition D =(B,E,V) built in the previous section and keep the notations introduced there. In this section, when we talk about a component of a set

Suppose now that (1) holds. Applying again Lemma 7.2, and the fact that A ∩R′= Ø(in B), one deduces that every component of A contains at most one ωi. Similarly, if (2)holds, every component of R contains at most one αi. In particular (1) and (2) cannot occur simultaneously.□

Proof of Theorem 1.1 As explained in Section 3 there exists a total orderon B,which is weaker than ≤, meaning that for every b, b′in B, we have:

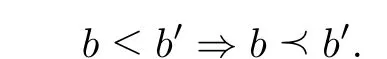
· Γ belongs to C-if there is a component of AΓcontaining every ωi;· Γ belongs to C+if there is a component of RΓcontaining every αi.It is clear that (C-,C+) is a cut of C. Note also that C-and C+are not empty because(Ø,B)∈C-and (B,Ø)∈C+.

Lemma 7.4 tells us that the cut (C-,C+) of C is a gap: C-has a maximum and C+has a minimum. In particular, there exists a brick b, uniquely defined, such that

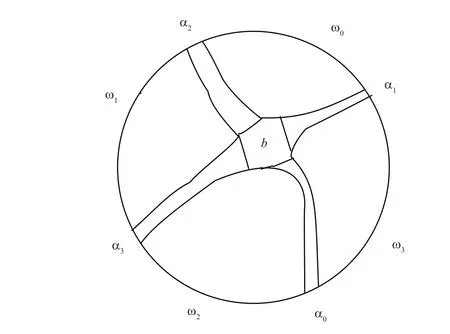
Figure 10

Remark 7.5 The underlying idea of Morse theory is to study a manifold by analyzing smooth functions defined on that manifold. If the manifold is compact and the critical points are not degenerate, the topology of the sublevels and superlevels change at every critical value and the change of topology can be understood relative to the Morse indices of the associated critical points. To prove such a thing, one needs to choose an adequate Riemannian metric on the manifold and to look at the dynamics of the associated gradient flow. In particular,if there is no critical value inside a segment[a,b],the sublevels{x ∈M|f(x)≤a}and{x ∈M|f(x)≤b}are diffeomorphic. More precisely, after a reparametrization of the gradient vector field, the first set is the image of the second one by the time one map of the induced flow. There are many non compact situations where one can prove the existence of critical points of a given smooth function, or more generally of singular points of a given gradient-like vector field, but one needs conditions at infinity to do so (for instance imposing the function to be quadratic at infinity when M can be written M =N ×Rn, where N is a compact manifold and n ≥1.)

The principle of our given proof is very similar, but stated in a discrete setting, with an argument by contradiction. We suppose that our map is non recurrent and start by choosing an adequate free brick decomposition. Then we transform this decomposition into a maximal one(we do not have any control on this construction). The set of bricks of this new decomposition is furnished with a natural order ≤and we extend this order into a maximal one(we still do not have any control on this extension). These objects (brick decomposition and total order) play the role of the Riemannian metric used in Morse theory. The cuts Γ play the role of level sets,with their sublevels AΓand their superlevels RΓ. We have a “condition at infinity” satisfied by the original chosen brick decomposition, consequence of the fundamental lemma. Now, from one side,there is a change of“topology”(expressed in terms of the behaviour at infinity)among the sublevels, and on the other side, there is no change of topology because every brick b being free, it holds that f(b)⊂φ+(b)⊂b≺(the bricks play the role of flow-boxes in the classical setting).

8 Further Comments About the Proof

8.1 Transverse foliations

Let γ : I →D be a path defined on a non trivial real interval. Say that γ is positively transverse to F if it locally crosses leaves from the right to the left. Such a path must be injective because F is non singular. In fact, as explained in [11], the space of leaves furnished with the quotient topology is an oriented one dimensional manifold, which is Hausdorffif and only if the foliation is trivial, meaning conjugate to the foliation of C by verticals. A positively transverse path projects onto a simple path in the manifold F, compatible with the natural orientation. Note that there is a natural order ≤on F defined as follows: λ ＜λ′if there exists a transverse path γ :[0,1]→D such that γ(0)∈λ and γ(1)∈λ′. Let us state now an easy but important result proved in [12]: for every z ∈D, there exists a positively transverse path that joins z to f(z). Noting φzthe leaf containing a point z ∈D, this result tells that the function zφzis a Lyapunov function of f with values in F: one has φf(z)＜φzfor every z ∈D.

Let us explain now how to use the foliated version of Brouwer Translation Theorem to prove that a homeomorphism satisfying the hypothesis of Theorem 1.1 has at least one fixed point.Here again, it will be a proof by contradiction. The simplest way to construct a transverse foliation is to start with a maximal free brick decomposition D = (B,E,V), to extend the order ≤naturally induced on B by a total orderand to consider the set L of lines λ ⊂Σ(D),where λ ∈L if and only if there exists a cut c = (Rc,Ac) ofsuch that λ is a connected component of ∂Rc= ∂Ac(see [14]). The orientation of Σ(D) defines a natural orientation on each λ ∈L,and then λ ∈L is a Brouwer line. There is a natural topology and a natural order on L(partial but locally total ) that makes L similar to a lamination(every λ has a neighborhood that is homeomorphic to a totally disconnected compact subset of a real interval). By a process of desingularization, one can “blow up” the space L and transform it into a real lamination of D by Brouwer lines, homeomorphic to L. To construct F, it remains to fill the complement of this lamination.

It is a natural question whether it is possible to construct a similar foliation in case f is not recurrent and get a complete proof of Theorem 1.1. The answer is probably yes. Nevertheless it is not clear if it will pertinent to try and do so. Let us give a first reason. To construct a transverse foliation for a Brouwer homeomorphism,it is necessary to prove first that there is no singular brick. The characterization that is given in Lemma 4.2 leads us to believe that singular bricks do not exist in the more general case of non recurrent map. But the proof will not be too easy and will certainly need to use topological arguments that cannot be expressed in terms of brick decompositions, like the majority of the arguments used here. In fact, singular bricks do not really cause problems (we will see very soon how to avoid them if necessary). A second reason not to use foliations is that the desingularisation and the filling processes necessary to get a foliation is quite complicated, long and not easy to write. Moreover,Brouwer lines should be replaced by more complex manifolds (unions of lines) like what is done in the thesis of Tran Ngoc Diep [20], where a Brouwer type foliation is constructed for some orientation reversing plane homeomorphisms.

8.2 As a conclusion