公路岩质高边坡稳定性及支护分析
2021-02-23卢应发
陈 昊, 卢应发, 谢 鹏, 陈 诚
(1 湖北工业大学土木建筑与环境学院,湖北 武汉 430068; 2 湖北省地质环境总站,湖北 黄石 435000)
在多山地区修筑公路的过程中难以避免的遇到众多复杂的地质环境,而路堑边坡破坏亦多不胜数,对其破坏机制、工程防治的研究是摆在公路建设者们面前的紧迫问题,众多学者的研究成果也被广泛应用于实际工程中,且已证明相关成果良好的普适性。对边坡内部力学研究,发展出诸如简布法、费伦纽斯法等传统条分法。陈祖煜[1]基于Spencer法提出三维形式极限平衡法,并证明其适用性;李同录等[2]改进了传统三维极限分析法,假定条柱分界面的极限平衡条件进而推导了相应公式。上述传统分析方法均做了不同假定从而导致其局限性较大,随着计算机相关技术的更新,应用大型数值计算程序成为研究边坡稳定的新途径,亦愈来愈受到相关学者重视。陈菲[3]基于FLAC3D探讨了强度折减法在三维边坡稳定分析中的工程应用问题;陈云生等[4]运用MIDAS GTS分析公路边坡开挖与支护前后位移、应变分布特征,并验证三维数值模拟的合理性。笔者在前人研究的基础上,以弹塑性有限元强度折减法为理论依据,对岩质公路高边坡在原始工况、削坡及加固治理后的稳定性进行分析,对类似边坡及治理有借鉴意义。
1 工程概况
该路堑边坡地处丘陵岗地区,坡顶高度为80 m,坡脚度为28 m,高差约50 m,长约200 m,平面图上大致呈“S”形,坡体走向近东西向,坡向146°,坡角55~85°,地形陡缓相间,前缘人工切坡较陡;坡体上覆有粉质粘土夹碎石块:黄褐色,厚度一般为1.5~2.5 m;碎石成份为主要为砂质岩,直径一般为5~20 cm,土石比为7:3;该层结构松散,属透水不含水层。下伏地层物质主要为灰岩夹泥质粉砂岩,中厚层状,岩层产状为350∠50°,单层厚2~5 cm局部夹煤系地层,薄层状。地下水类型为孔隙水,补给来源主要为大气降水入渗。

图 1 边坡特征示意图
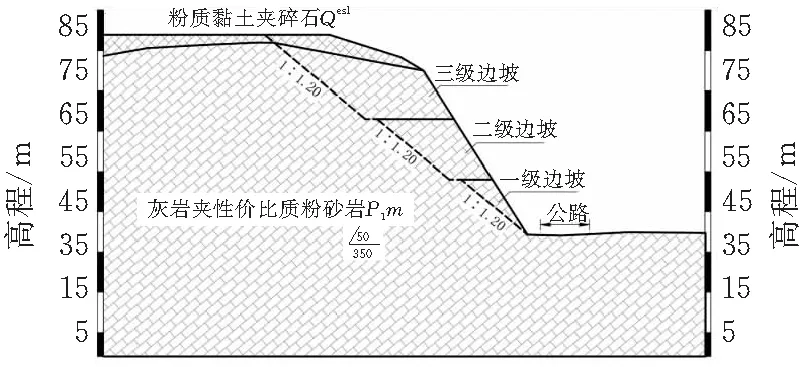
图 2 边坡断面及开挖示意图
由于人工切坡,岩体受风化程度强烈,结构多呈碎裂状,裂隙十分发育,主要发育有二组节理:1)组160°∠52°,间距10~20 cm,裂面平直,延展大于1 m;2) 组120°∠69°,间距10 cm左右,裂面平直,延展一般小于1 m;闭合状,无充填。由于局部构造影响,边坡局部岩体的产状变化不规律,褶皱发育较明显,产状为35°∠90°、175°∠4°、230°∠67°、85°∠38°。边坡岩体介质软硬相间、节理裂隙切割强烈,局部褶皱较发育,岩质边坡发生破坏是由于岩体中软弱结构面的抗剪强度逐渐降低,加之风化剥蚀、临空卸荷与降雨入渗等因素影响,为了防止发生进一步破坏对坡脚公路通行造成影响,决定对边坡进行削坡减重、设置框格梁和预应力锚杆等加固方法进行工程治理。
对边坡削方开挖采取三级开挖,均采用1∶1.2的比例系数进行放坡,中间设3 m宽马道。预应力锚杆:L=15 m,采用直径为32 mm的HRB400螺纹钢筋,布置间距4 m;框格梁截面尺寸:0.5 m×0.4 m,采用C30混凝土浇筑。
2 数值模拟
2.1 有限元强度折减法
通过将坡体强度参数:用折减系数Fs来不断降低粘聚力c和内摩擦角φ值,将得到的c′和φ′继续折减,直至计算失稳。本文选取的失稳判据为:分析步骤中力和位移值计算不收敛。
c′=c/Fs
tanφ′=tanφ/Fs
τ′=c′+σtanφ′
式中:Fs为强度折减系数,c′、φ′、τ′分别为折减后的粘聚力、内摩擦角、抗剪强度。
2.2 本构模型
本次有限元计算选取弹塑性模型,德朗克-普拉格(Drucker-Prager)屈服准则,其数学表达式为:
I1=σ1+σ2+σ3
式中:α和k为与粘聚力、内摩擦角相关的参数,I1为应力张量第一不变量,J2为应力偏张量第二不变量。
2.3 路堑边坡模型建立
本次模拟建立的三维地层模型由三角形网格划分生成,计算模型尺寸:x=180 m;y=20 m;Z=80 m,共有18 599个节点,31 655个单元(图3)。边界条件:临空面设置为自由边界,前后、左右边界施加法向固定约束,将坡脚处网格延伸一定长度是为了消除边界效应对坡脚处模拟结果的影响。支护结构的框格梁用梁单元实现,预应力锚杆用桁架单元实现(图4)。

图 3 有限元模型网格划分图

图 4 框格梁、锚杆有限单元图
2.4 坡体相关参数的选取
坡体相关参数见表1。
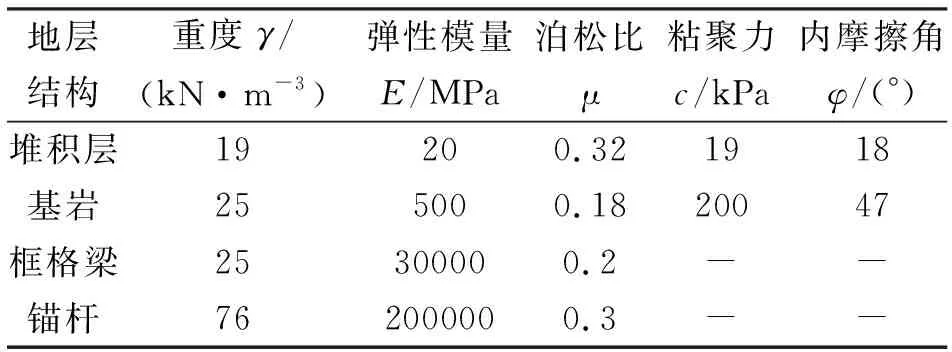
表1 坡体、支护材料参数
3 模拟结果分析
3.1 未开挖状态结果及分析
原始状态下对坡体进行分析后得出的水平位移、剪应变分布云图(图5)。在不做任何加固措施的边坡稳定性系数为1.181,介于规范中规定1.05~1.30,即边坡处于基本稳定状态;原始状态下的坡体的坡度较陡,坡体受自重影响较大,坡脚处的应力集中明显,坡体出现滑移,由应变图看出塑性范围从坡脚一直贯通至坡顶,且呈圆弧形,推测此层面为软弱层,坡脚处水平位移最大达到1.084 m,由于坡脚承受上部全部荷载,此时的坡脚处抗剪能力不足,一旦坡体抗剪强度极限达到,将会发生失稳直至破坏,故有必要对其进行削方减载。

图 5 原始状态下的位移、应变分布云图
3.2 开挖后结果分析
1)位移场分析 如图6中边坡开挖位移图所示,在第三级边坡开挖完毕后,坡体水平位移最大值为0.292 m,表明经过坡顶减载后,坡体整体受到自重应力大幅下降,稳定性有所提高;随着第二级边坡的开挖完成,水平位移最大值减小为0.196 m,坡体自重影响逐渐减小;第一级坡开挖完毕后,位移继续减小至0.176 m, 这是由于第三级坡和第二级坡的方量较大,在完成削方减载后,坡体的位移值有较大变化,第一级边坡方量较小,故减小幅度稍小,对比在未开挖前的最大位移值,各阶段的最大位移值在上一阶段的基础上分别减小73%、32%、10%。
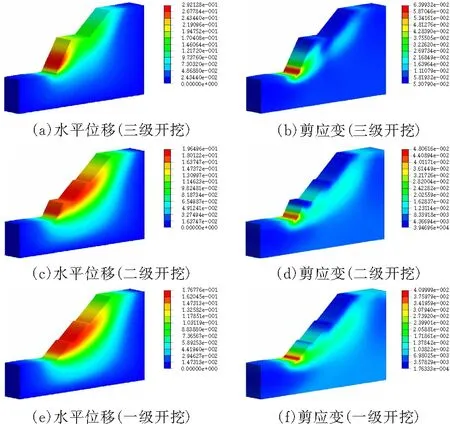
图 6 未支护工况下各阶段位移、应变分布云图
2)应变场分析 由应变云图可知,第三级边坡开挖完成后的剪应变最大值为0.064,此时塑性区主要集中于未开挖坡体,边坡最危险滑移区处于坡脚处;第二级边坡开挖后由于危险结构面出露,塑性区有发育趋势,剪应变最大值减小为0.048;最大剪应变在上一阶段的基础上分别减小82%、23%、35%,以上分析表明随着开挖施工进行,坡体发生剪切破坏的机率是不断减小的。
边坡开挖完毕后的整体安全系数为1.357。对于坡度较陡边坡,按一定放坡系数进行削方减载有助于降低发生破坏的风险,这也是工程界的常用治理手段,随着边坡的开挖进行,坡体结构内部会发生应力重分布以达到新的平衡稳态,总体趋向稳定形态发展。为了降低后期人为、环境因素对减载后边坡的影响,使边坡形态能长期保持,必须辅以进一步的加固措施。
3.3 支护后结果分析
1)位移场分析 图7、图8分别为框格梁、框格梁+预应力锚杆逐级加固后的边坡云图。对不同加固措施下的边坡位移场进行分析可知:
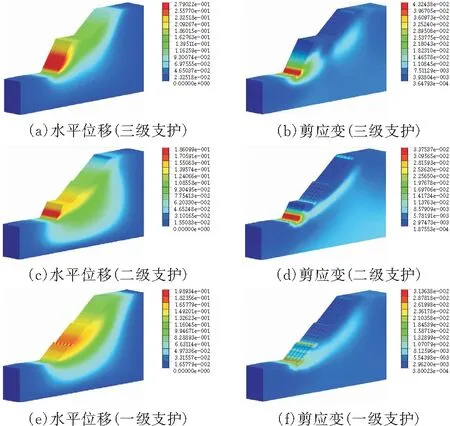
图 7 框格梁加固后位移、应变分布云图
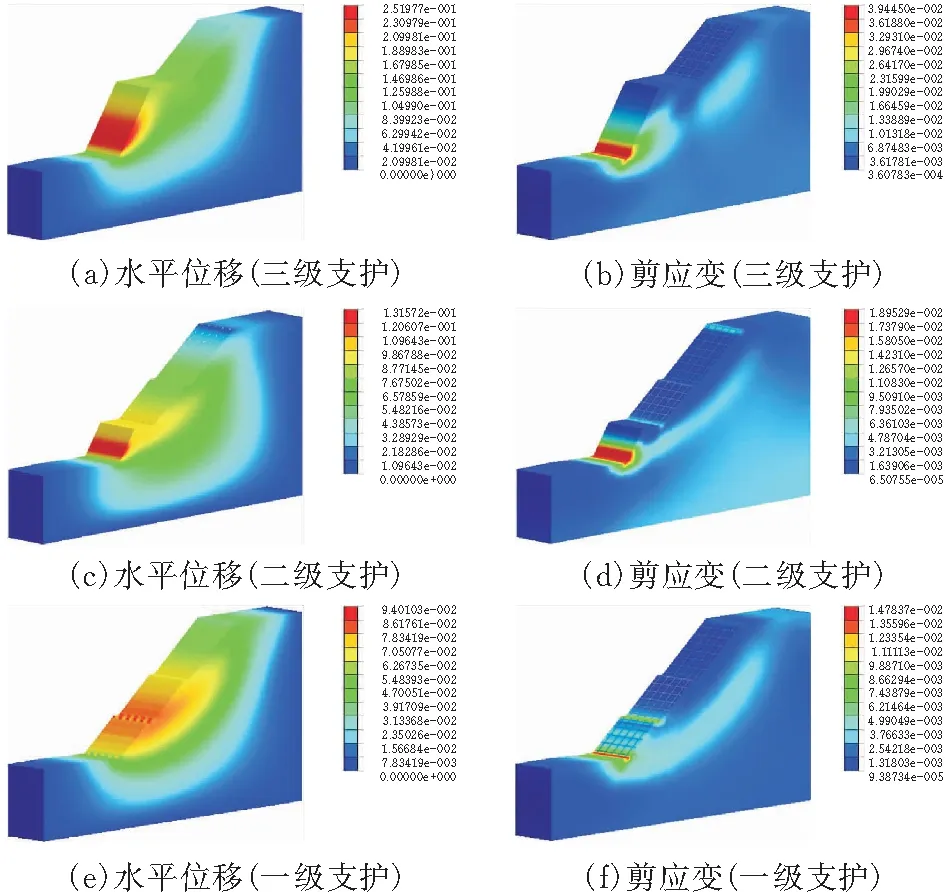
图 8 框格梁+预应力锚杆加固后位移、应变分布云图
在仅采用框格梁加固下,第三级边坡位移量最大值为0.279 m,与开挖未加固的结果相差不大,可知第三级边坡开挖和加固对边坡位移发展的约束作用有限,坡脚处发生剪切破坏可能性仍较大;第二级边坡、第一级边坡加固后位移量最大值分别为0.186 m、0.198 m,结果有所增大,主要是由于框格梁在施工浇筑的过程中打破了边坡静力平衡,使边坡受重力荷载有所加大。
采用框格梁+预应力锚杆加固后各阶段的位移量最大值为0.251 m、0.131 m、0.094 m,较仅采用框格梁加固减小明显,表明预应力锚杆的介入极大改善了边坡变形趋势,锚杆的作用是连接坡体表面风化岩和坡体内部新鲜基岩,锚杆借助坡体深处基岩的内聚力,有效释放深处岩石之间的胶结力,用来抵消向坡体浅层一定深度范围内的风化岩体因强度消散产生下滑的下滑力,从而发挥加固效能,在框格梁+预应力锚杆两者共同作用下为坡体具有长期稳固形态提供基础。
2)应变场分析 由图7和图8应变云图可知:采用框格梁加固下的最大剪应变相较于未加固各阶段分别减小32%、30%、23%,边坡整体安全系数为1.429。采用框格梁+预应力锚杆加固下的最大剪应变相较于未加固各阶段分别减小38%、61%、64%,边坡整体安全系数为1.851。
两种加固方式下均能明显减弱塑性区的发育,塑性区逐渐收窄。最大剪应变区仅存在二级坡脚和一级坡脚处很小范围内,表明经过加固后对边坡起到很好支护作用。综上所述,通过对比分析后得出采用框格梁+预应力锚杆是本治理工程的首选方案。
4 结论
1)对公路高边坡的开挖计算结果得出:原始边坡的稳定性系数为1.181,尤其在坡脚处的应力集中明显,若不进行开挖治理,随着时间的推移,坡脚最先会发生失稳破坏;在三级边坡开挖的过程中,坡脚承受自重应力影响逐渐减小,稳定性是逐步加强的,在开挖完毕后坡脚处仍存在部分应力集中。
2)通过对公路高边坡的支护治理后可知:在框格梁的加固作用下的稳定系数为1.429,相较开挖后支护前的稳定系数1.357,增幅不大,表明其未对坡体的位移产生很好的约束;框格梁+预应力锚杆的组合加固措施则展示其优异的阻滑性能,稳定系数增大至1.851,达到了预期的治理效果。施工过程中,建议在坡顶和坡脚处构筑截水沟,防止雨季的降雨入渗对加固工程的危害。
