预应力锚杆框格梁加固岩质边坡计算方法研究
2019-05-14侯俊伟吴曙光
侯俊伟,吴曙光
(1. 中煤科工集团重庆设计研究院有限公司,重庆 400042; 2. 重庆大学 土木工程学院, 重庆 400045)
0 引 言
依据现行规范,预应力锚杆框格体系一般按静力学原理进行设计和计算。当锚固点变形较小时,钢筋混凝土格构式锚杆挡墙可简化为支撑在锚固点上的井字梁进行内力计算;当锚固点变形较大时,应考虑变形对格构式挡墙内力的影响。预应力锚杆格构体系虽己广泛应用在边坡支护工程中,但国家标准或行业标准设计规范中尚未对其设计原则、计算模型和方法等做出具体规定。因此,对于预应力锚杆框格体系中钢筋混凝土框格梁,一般按梁底受均布荷载的状况进行计算和设计,这与框格梁的实际受力情况并不一致,特别是在锚杆框格体系应用于岩质边坡加固的情况下。与土质边坡不同,在岩质边坡上的框格梁反力分布很不均匀,其反力呈锚杆结点下集中的趋势,岩体质量越好,框格梁相对柔性越大,这种集中趋势就越显著(图1)。按照实际反力计算结果框格梁内力较小,可大幅节约材料。

图1 预应力锚杆框格梁梁底反力分布
目前对岩质边坡锚杆框格体系中框格梁的计算研究还不完全成熟或实用。郭继武[1]采用普通连续梁法和调整倒置梁法计算地基梁的内力和位移。倒置梁法是将框格梁坡面反力视为作用在梁上的线性荷载,把预应力锚杆作用点看作支座,将框架作为倒置的交叉框格体系进行计算;梁瑶等[2]将框格梁锚索体系划分为张拉阶段和工作阶段,提出利用滑坡推力确定作用在框架梁上的反力,用倒置梁法反推锚索拉力从而计算出梁的内力;白雪峰[3]提出预应力锚杆与砼框格梁作为相互关联的整体结构的设计计算方法,进而优化应用于边坡加固设计中的预应力锚杆框格梁;韩冬冬等[4]通过 1∶2 比例尺的大型物理模型试验,分析研究了预应力锚杆框格梁的基底反力分布规律;周志刚[5]通过双参数弹性地基梁初参数法的推导,确定了框格梁上锚杆间距的合理范围,并运用弹性理论分析了预应力锚杆框格梁加固边坡的受力机理,得到了坡体内附加应力及位移的分布规律。目前针对岩质边坡的预应力锚杆格构梁计算方法研究相对较少,部分计算理论过于繁琐。因此,应加强预应力锚杆框格支挡结构的设计计算理论及传力机理的研究。
1 基于锚杆框格支挡结构与边坡岩体相互作用的优化设计思路
在岩质边坡情况下,由于锚杆的拉力作用,框格梁对边坡坡面岩体产生压力作用;同样,当边坡坡面岩体发生下滑或有下滑趋势时,坡面岩体下滑将对紧贴其上的框格梁产生反力作用。因此,在这一过程中,应该将框格梁、锚杆和边坡岩体这三者视为一个系统,进行整体分析。如果直接对这三者进行建模分析,可运用数值模拟技术来实现,但建模过程极其复杂,最后的分析工作量也相当大。
在实际计算及设计过程中,从实用性的角度出发,可将锚杆框格体系和边坡岩体这一系统进行一定程度的简化,具体计算过程如下:
1)分析边坡稳定性,根据边坡稳定性安全系数计算锚杆支护力。
2)进行锚杆设计。
3)将框格梁视为支撑在锚固点上的井字梁进行内力计算及配筋设计。在进行框格梁梁底反力和内力计算时,考虑框格梁与边坡岩体的相互作用。
2 文克尔地基模型的应用
对于岩质边坡采用锚杆框格梁进行支护。由于边坡岩体强度较高,框格梁的刚度相对于地基较小,跨越作用很弱。这样锚杆结点荷载通过框格梁传到坡面时,不可能向两边大量扩散,就像直接作用在地基上一样。当框格梁细长而边坡岩体强度很高时,框格梁的挠度和梁底反力只在锚杆结点附近的局部范围内比较显著,在较远处就迅速衰减而趋于零。这种只在作用点局部范围内产生应力和变形的特点正符合文克尔地基模型所描述的特征。因此,运用文克尔地基模型对岩质边坡上框格梁的内力计算进行分析是合适的。
文克尔地基模型是假设地基表面任一点单位面积内所受的压应力p(x,y)与相应的地基竖向位移ω成正比关系,亦即
p(x,y)=k·ω
(1)
式中:p(x,y)为基底反力,kPa;ω为地基竖向位移,m;k为基床系数,kN/m3。
根据文克尔假定,可推知框格梁的挠曲微分方程为
(2)
式中:E为框格梁的弹性模量,kPa;I为框格梁的惯性矩,m4;b为框格梁的宽度,m;q为框格梁上荷载,kN/m。
引入梁的柔度指数λ(单位:1/m):
(3)
则:框格梁的通解为
ω=eλx(c1cosλx+c2sinλx)+e-λx(c3cosλx+c4sinλx)
(4)
式中:c1~c4为待定积分常数,可由荷载位置及边界条件确定。
框格梁的柔度指数λ反映了框格梁相对于地基的柔性程度,λ值越大,则梁柔性越大。考虑到荷载作用位置、相对刚度对计算位移和内力的影响,可以根据梁的柔度指数λ和长度l以及荷载距梁端的距离x,将梁划分为:刚性梁(λl≤1)、有限长梁(1<λl<2.75)、无限长梁 (λl≥2.75)。在大多情况下,岩质边坡上框格梁属于有限长梁,笔者主要针对有限长梁的简化计算方法进行研究。
由于文克尔假定没有考虑地基中剪应力的影响,存在不能扩散应力和变形的缺陷,不过,鉴于其模型简单,较容易计算,故在工程设计中仍被广泛采用。
3 岩石地基基床系数取值分析
用文克尔地基模型进行计算时,框格梁的内力计算跟基床系数k有很大关系,若k值取得过小,则内力计算结果偏大,将导致成本增加;若k值取得偏大,则会降低设计的安全性。这就需要确定一个最优的k值,使得设计本身既能保证足够的安全程度,又能达到设计优化的要求。
影响k值的因素很多,除了边坡岩体本身的性质以外,还有梁的大小和形状、刚度等。目前,确定地基基床系数的方法主要有现场载荷板试验法、利用分层总和法按土的压缩性指标计算法、弹性半空间地基沉降模型反算法等。由于在土质地基上进行现场载荷试验比较容易,因此积累的经验数值也很多。各种规范和规程中对水平方向基床系数的取值都按照土的不同类别建议了一些经验的取值范围,但这些范围普遍偏大,有的甚至相差几倍。由于在岩石地基上进行现场载荷试验很困难,因此资料相对较少,大多资料提供的k值仅分软质岩(200~1 000 MPa/m)和硬质岩(1 000~15 000 MPa/m)两种,由于数据分类过粗,不利设计人员选取使用。
对于笔者主要讨论的重庆地区,常见岩层是泥岩和砂岩。通过研究发现,基床系数k与岩石单轴抗压强度frk之间存在一定的关系,这为获取基床系数找到了新的途径。
岩石单轴受压的破坏机制,虽然与地基的破坏机制有所不同,但岩石的单轴抗压强度基本上能反映岩石的力学性质,已被国内外公认为衡量岩石的质量指标。根据重庆岩基站在岩石地基上进行的现场载荷试验结果和相应的室内试验结果[6],通过回归分析,得到的基床系数k和岩石单轴抗压强度frk的关系式
(5)
将式(5)绘制成曲线,与现场载荷试验得到的结果以及从国内文献资料中收集的k值进行对比可知,用岩石单轴抗压强度来换算k值是简单可行的。对于岩质边坡,应采用水平方向基床系数kh,它可通过基床系数进行适当折减得到,折减系数约0.8,从而近似得到岩质边坡水平基床系数和岩石单轴抗压强度的关系式:
(6)
4 框格梁内力简化计算方法
4.1 基本思路
弹性地基梁的计算较为繁杂,如果没有计算机的帮助,按理论方法进行手算工作量很大。可通过一定的简化处理,进行简化计算。框格结点的锚杆荷载分配到纵、横两框格梁后,其内力便可按单向连续梁的方法进行计算。锚杆荷载按竖向变形协调分配时采用的地基模型,在按单向连续梁计算内力时也宜采用同样的模型[2]。
对于有限长梁,框格梁的纵梁(x方向)和横梁 (y方向)共同承担锚杆锚固力,按地基上十字交叉梁与岩体的共同作用来计算。为简化计算,将框格梁简化为地基上正交交叉梁系,分别为两个方向的地基上梁,一般不考虑结点上的扭转变形协调,而只要求满足结点的静力平衡和变形协调条件,即假定框格梁在十字交叉结点处纵横两个方向为铰接(上、下用链杆连接),这就可认为一个方向的梁在该方向的力矩作用下发生转角,不可能引起另一方向梁的扭转和扭矩。通过对交叉点处荷载进行分配,然后分别按纵、横两个方向的地基梁来计算。
1966年,美国混凝土学会(ACI)436委员会对联合基础(承受2个柱荷载以上的基础)和片筏基础推荐了一种简化计算法。笔者参照该法提出框格梁内力的简化算法。
在文克尔地基模型的基础上,假设框格梁底反力在锚杆结点下最大、跨中最小,在锚杆结点与跨中之间按直线分布,因此框格梁底反力成折线图形(图2)。根据集中荷载作用于无限长梁的弹性地基梁解和取单跨的静力平衡条件,可推导出框格梁底反力和框格梁内弯距的简化计算公式。
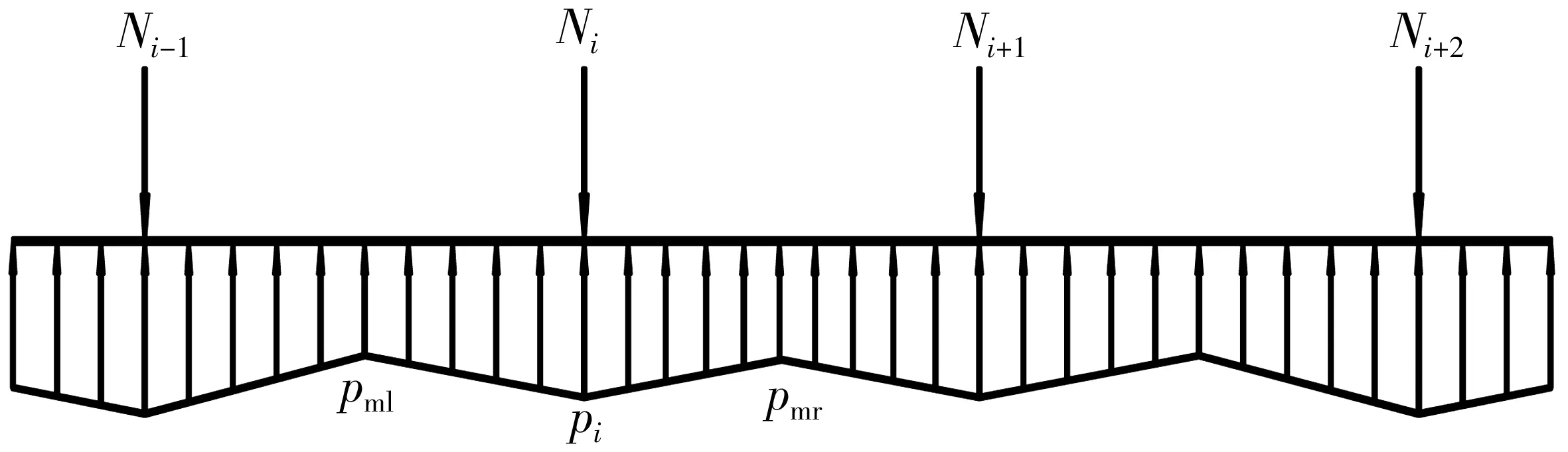
图2 框格梁的梁底反力分布
4.2 总的原则和基本假设
1)跨度不少于3跨。
2)相邻两结点锚杆荷载的变化不大于20%。
3)相邻两结点间距的变化不大于20%,通常情况下锚杆按等间距设置。
5)在跨中到相邻跨跨中之间,梁底反力的合力与梁上锚杆和与梁垂直方向分力大小相等、方向相反,并在同一条水平线上。
6)忽略梁自重对其内力的影响。
4.3 框格梁底反力和框格梁内力计算
4.3.1 中间锚杆结点处框格梁的弯矩
根据文克尔理论,对于一无限长梁上受集中力作用的情况,梁内弯矩可按式(7)计算[3]:
(7)
式中:M(x)为梁内x位置处的弯矩,kN·m;N为梁上所受集中力,kN;F3为λx的函数计算式;其它符号同前。
如果有若干集中荷载作用在无限长梁上,则梁上某截面的弯矩为各集中荷载对该截面的总和。图3表示各中结点的弯矩和梁底反力分布。
研究证明,如果符合前面所述假设,在计算中间锚杆结点i截面处框格梁的弯矩时,式(7)中的三角函数F3(λx)可以近似地用一条直线代替,Mi(x)可近似地按式(8)计算:
(8)
式中:Ni为锚杆i提供的水平分力,kN;a为锚杆竖向间距,m。
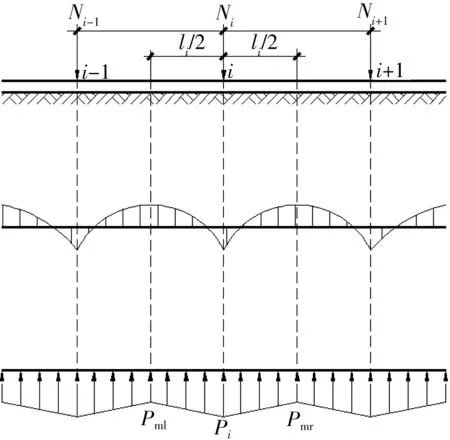
图3 中结点的弯矩和框格梁的梁底反力分布
4.3.2 中间锚杆结点处梁底反力
设锚杆i左、右两跨的跨中梁底反力为pml和pmr,则平均跨中梁底反力为
(9)
从跨中到相邻跨跨中取出一跨,根据基本假设5),得:
(10)
则:
(11)
取出一跨作为脱离体,将锚杆结点处看成固定端,并将梁底反力作为荷载,如图4。

图4 计算简图

(12)
式中:Mi为i截面的弯矩,kN·m,按式(8)计算。
将式(11)代入式(12),得锚杆结点下基底反力pi的表达式:
(13)
在计算跨中基底反力时,取跨中到临近跨中为一单元,由上述假设以及静力平衡条件得
{Ni=12(pml+pi)·12ll+12(pmr+pi)·12lr
12(pml+pi)·2pml+pipml+pi·l2l12=12(pmr+pi)·
2pmr+pipmr+pi·l2r12
(16)
联立求解式(16)得
根据美国混凝土学会(ACI)1966年对联合基础和片筏基础推荐计算法结论[7],跨中梁底反力为:
(14)
式中:pml、pmr分别为i结点左、右两跨跨中的梁底反力,kN/m。
对于锚杆等间距布置的情况,由于ll=lr=l,则:
(15)
将式(13)代入式(15),得
(16)
4.3.3 框格梁跨中弯矩
计算出结点处梁的弯矩以及梁底反力后,可将相邻两结点间的一段梁作为脱离体,按平衡条件计算跨中弯矩(图5):
(17)
(18)
式中:M0为对应简支梁时跨中弯矩。

图5 框格梁跨中弯矩
4.3.4 边结点处梁底弯矩及反力
框格梁外伸长度较短时,可以假定外伸部分梁底反力呈均匀分布(图6),则框格梁边节点集中力N1(单位:kN)按式(19)计算,反力线荷载p1(单位:kN/m)按式(20)计算:
(19)
(20)
边结点处梁弯矩M1为
(21)

图6 边结点处弯矩、反力分布
5 算 例
某受外倾节理面控制的岩质边坡[8],坡高12 m,设计放坡坡率为1∶1,采用预应力锚索框格梁支护,框格梁纵、横向间距均为4.0 m,悬臂段2.0 m,梁长12.0 m。设计锚索为6束Φ15.2 mm钢绞线,按照每孔锚索可承受T=900 kN的设计拉力,超张拉15%锁定,水平夹角15°,横梁和纵梁横截面尺寸均为60 cm × 60 cm。边坡岩石天然单轴抗压强度值为10.0 MPa。
根据传统倒梁法计算理论,基本假定:将坡面反力视为作用在框架上的荷载,把预应力锚索作为铰支座,将框格梁作为倒置的交叉梁格体系来进行计算;假定坡面反力呈均匀直线分部,将横梁和纵梁看成相互独立的连续梁;忽略梁自重及侧阻力影响。图7为框格梁计算简图。
按照简化文克尔地基梁法,在进行框格梁梁底反力和内力计算时,考虑框格梁与边坡岩体的相互作用,框格梁底反力成折线分部,岩质边坡水平基床系数kh按照式(6)计算,kh=100 MPa/m。传统倒梁法及简化弹性地基梁法计算结果见表1。

表1 框格梁内力计算结果
注:PC、PD分别为C、D点的梁底反力,kN/m。
由表1可以看出,与常规设计法相比,采用简化文克尔地基梁模型计算框格梁内力,框格梁的中间锚杆结点处弯矩减小约35%,因此截面配筋设计等可得到明显优化[9]。
根据现行GB 50330—2013《建筑边坡工程技术规范》对框格梁计算的要求,将预应力锚杆框格梁简化为单元梁,按支撑在锚固点上的井字梁进行内力计算,一般未考虑边坡与岩体相互作用影响。笔者提出的简化计算方法,考虑了框格梁与边坡岩体的相互作用,计算模型更加符合实际预应力锚杆框格梁受力机理。从算例对比看出,框格梁截面尺寸及配筋计算等得到优化,该计算方法更加可靠经济。不过,简化计算方法有一定的适用条件,计算时应满足4.2的原则和基本假设。
6 结 论
1)地基基床系数可用岩石天然状态下的单轴抗压强度折算近似得到;对于岩质边坡,采用的水平方向基床系数,可通过竖向基床系数进行适当折减得到。
2)根据框格梁刚度的不同,将框格梁分为刚性梁、有限长梁、无限长梁等,分别提出了不同类型框格梁内力的简化计算公式。
3)提出了岩质边坡预应力锚杆框格梁内力简化计算方法,与常规设计法相比,框格梁的截面和配筋设计得到了优化,计算方法合理实用。
