ON F(p,q,s) SPACES*

Ruhan ZHAO

Department of Mathematics, SUNY Brockport, Brockport, NY 14420, USA E-mail: rzhao@brockport.edu

Abstract The family of spaces F(p,q,s)was introduced by the author in 1996. Since then,there has been great development in the theory of these spaces, due to the fact that these spaces include many classical function spaces, and have connections with many other areas of mathematics. In this survey we present some basic properties and recent results on F(p,q,s)spaces.

Key words F(p,q,s)spaces,Qs spaces,α-Bloch spaces,BMOA,weighted Dirichlet spaces,weighted Bergman spaces, Hardy space, Riemann-Stieltjes operators, pointwise multiplication operators.

1 Introduction

Classical spaces of analytic functions, such as weighted Bergman spaces,weighted Dirichlet spaces, analytic Besov spaces, the Hardy space H, the Bloch space, the space of analytic functions of bounded mean oscillation (BMOA) and the fairly recently introduced Qspaces,have their origins in a variety of backgrounds, and the theories of these spaces have been developed independently. All of these spaces have,however,found applications in many different areas of mathematics. In 1996,the author introduced in[71]a general family of analytic function spaces called F(p,q,s) spaces which depends on three real parameters: p, q and s. This family includes all of the spaces mentioned above,and therefore provides a unified treatment for these classical function spaces. Since their introduction,F(p,q,s)spaces have attracted the attention of mathematicians from all over the world, and there has been great development in the theory of F(p,q,s) spaces, with many interesting results and applications having been found. This survey presents some basic properties and some recent results on F(p,q,s) spaces.

Let us give the definition of F(p,q,s) spaces first. Let D = {z ∈C : |z| ＜1} be the open unit disk in the complex plane C. Let H(D) be the space of all analytic functions on D. For a ∈D, let φbe the M¨obius transformation on D given by

For convenience, we also say that F(p,q,0)=F(p,q,0).

Throughout this paper, constants are denoted by C. They are positive, and may differ from one occurrence to the other. The notation a ≾b means that there is a positive constant C such that a ≤Cb. Moreover,a ≈b means that both a ≾b and b ≾a hold.

2 F(p,q,s) Spaces and Some Classical Function Spaces

In this section we point out connections of F(p,q,s) spaces with some classical function spaces. We need the following notation: let 0 ＜r ＜1 and let a ∈D. We set

and call it a pseudo-hyperbolic disk in D. Let |D(a,r)| denote the area of D(a,r). It is well known that, for z ∈D(a,r),

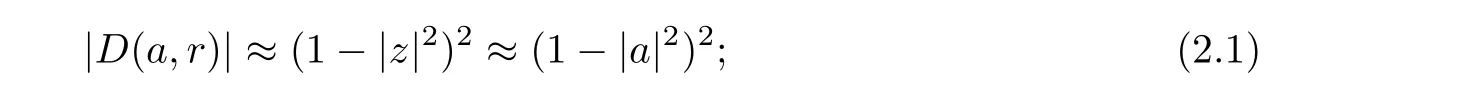
see, for example, (4.8) and (4.9) in [78]. Note that (4.9) in [78] uses a hyperbolic disk, while D(a,r) here is a pseudo-hyperbolic disk. However, from Proposition 4.4 in [78] it is clear that|D(a,r)|≈(1-|a|). We need the following well-known integral estimate:

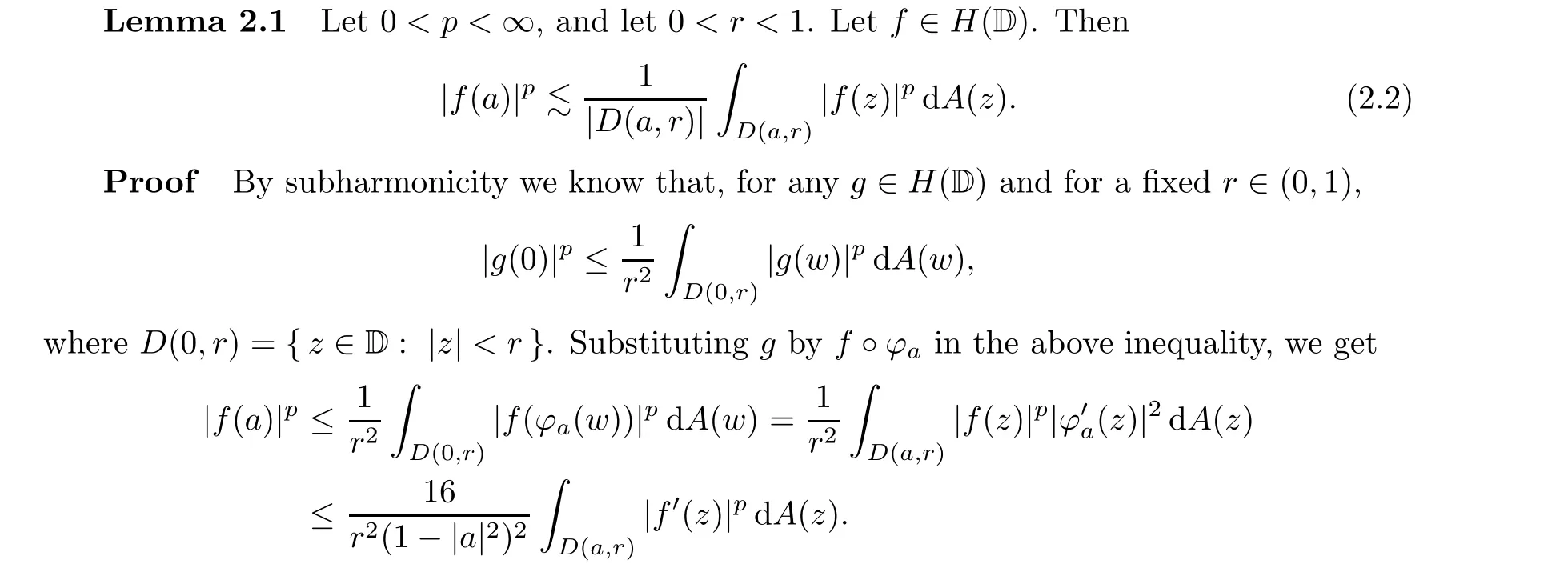
The Bloch space and the little Bloch space have been extensively studied by many authors;see, for example, [1, 7, 15] and [78, Chapter 5]. α-Bloch spaces and little α-Bloch spaces generalize the Bloch space and the little Bloch space. For references,see, for example,[76] and[70].

The following theorem from [70] gives some characterizations of B, and is crucial for the study of F(p,q,s) spaces:It is an elementary calculation to show that the last integral is finite for 1 ＜s ＜∞. Hence(E)≾(A), and the proof is complete.□

The little-oh case of the above result, as shown below, is also given in [70]. The proof is similar, so we omit the details.

Theorem 2.4 Let 0 ＜α ＜∞, 0 ＜r ＜1, 0 ＜p ＜∞and 1 ＜s ＜∞. Let f ∈H(D).Then the following statements are equivalent:

3 Basic Properties

In this section we show some basic properties of F(p,q,s) spaces. Most of the results in this section are from[71]. We first show the connections between F(p,q,s)spaces and Carleson measures.

The classical Carleson measure was introduced by Carleson [20] for studying the problem of interpolation by bounded analytic functions and for solving the famous corona problem.Later on it was found that the Carleson measure is very useful in many problems in function space theory and operator theory. Variations of the Carleson measure, such as the following s-Carleson measures, have been also introduced and studied:

Definition 3.1 For 0 ＜s ＜∞, we say that a positive measure μ defined on D is a(bounded) s-Carleson measure provided that

for all arcs I of ∂D, where |I| denotes the normalized arc length of I ⊆∂D and S(I) denotes the Carleson box based on I, that is,

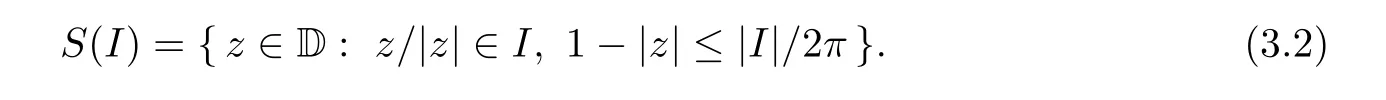
For s = 1, the s-Carleson measure is the classical Carleson measure. If the righthand side of(3.1) is o(|I|) as |I|→0, then we say that μ is a vanishing s-Carleson measure.

The following characterization is from [12]:

Lemma 3.2 For 0 ＜s ＜∞, a positive measure μ on D is a bounded s-Carleson measure if and only if

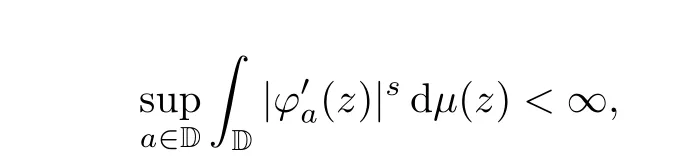
and μ is a vanishing s-Carleson measure if and only if

The following characterizations of F(p,q,s) spaces and F(p,q,s) spaces using Carleson measures are from [71]:

Theorem 3.3 Let 0 ＜p ＜∞, -2 ＜q ＜∞, 0 ＜s ＜∞satisfy q +s ＞-1, let f be analytic on D, and let dμ(z)=|f(z)|(1-|z|)dA(z). Then the following statements are equivalent:

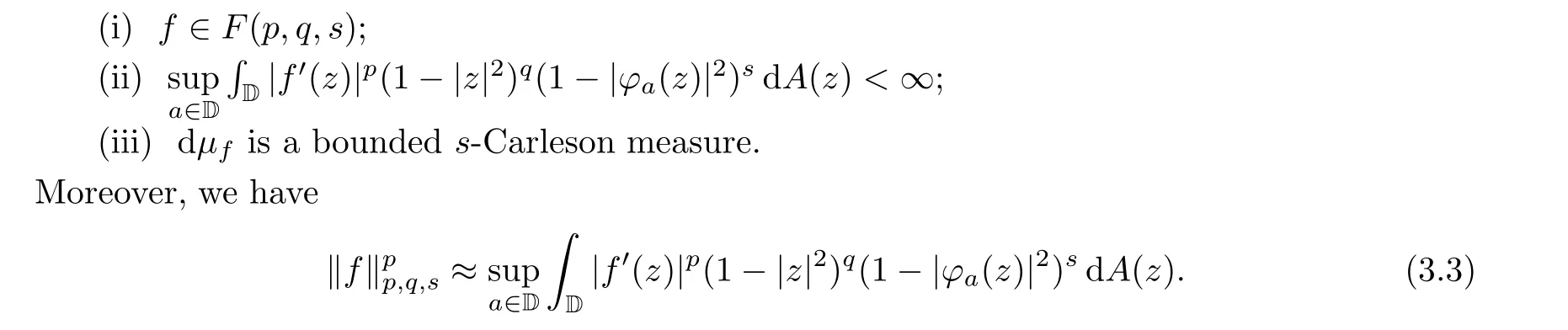
For the little-oh case, the following statements are equivalent:

which means that f ∈F(p,q,s), or (i) is true. Carefully examining the above proof we can see that (3.3) is true.

The proof of equivalences among (iv)-(vi) is similar, so we omit the details here.□

Remark If we define a bounded 0-Carleson measure as a bounded measure on D, then the result on equivalences among (i)-(iii) in Theorem 3.3 can be extended to the case s=0.

It is known that a vanishing s-Carleson measure is a bounded s-Carleson measure. Thus,as an immediate consequence of Theorem 3.3, we get the following inclusion relation:

Corollary 3.4 Let 0 ＜p ＜∞, -2 ＜q ＜∞and 0 ＜s ＜∞satisfy q+s ＞-1. Then

and F(p,q,s) is a closed subspace of F(p,q,s).

For a proof, we refer to the proofs of Theorem 2.10 and Proposition 2.15 in [71]. Next, we show that F(p,q,s) is not separable, and F(p,q,s) is the closure of polynomials in F(p,q,s).Part(ii) of the next theorem was first given as Proposition 2.3 in [38]. The proof for (ii) below is different from the proof in [38].

Theorem 3.10 Let 0 ＜p ＜∞, -2 ＜q ＜∞, 0 ＜s ＜∞satisfy q+s ＞-1. Then we have the following results:

(i) F(p,q,s) is not separable.

(ii) Let f be an analytic function on D, and for 0 ＜r ＜1 let f(z) = f(rz). Then f ∈F(p,q,s) if and only if ‖f-f‖→0 as r →1. In particular, F(p,q,s) is the closure of all polynomials in F(p,q,s), and F(p,q,s) is separable.

Hence F(p,q,s) is not separable.

(ii) Suppose that ‖f- f‖→0 as r →1. It is easy to see that, for any fixed r ∈(0,1), f∈F(p,q,s). By Theorem 3.9, F(p,q,s) is a closed subspace of F(p,q,s). Thus,f ∈F(p,q,s).

Conversely, suppose that f ∈F(p,q,s). We follow the proof of Proposition 2.3 in [2]. By Theorem 3.3, for any ε ＞0, there exists δ ＞0 such that

Definition 3.11 A Banach space of complex functions on a set X is called a functional Banach space on X if the vector operations are the pointwise operations, f(x)=g(x) for each x in X implies that f =g,f(x)=f(y)for each function f in the space implies that x=y,and for each x in X, the point evaluation K: f →f(x) is a continuous linear functional.

From Proposition 2.5 we can easily see that the point evaluation K: f →f(z) is a continuous linear functional in F(p,q,s) (cf. [71, Proposition 2.11]), and hence we can get the following result ([71, Proposition 2.17]):

Proposition 3.12 Let 1 ≤p ＜∞, -2 ＜q ＜∞, 0 ≤s ＜∞and q +s ＞-1. Then F(p,q,s) and F(p,q,s) are functional Banach spaces on D.

4 Typical Examples of Functions in F(p,q,s)

For many problems involving properties of F(p,q,s)spaces or some operators on F(p,q,s),one may need to know some concrete examples of functions in these spaces. Polynomials are examples for each F(p,q,s), but they are not typical. Here we provide two types of typical functions in F(p,q,s).

The first type resembles reproducing kernels for some Hilbert spaces. For this type, we need the integral estimation obtained by Zhang, Li, Sheng and Guo in [68], which generalizes an earlier result by Ortega and F`abrega in [41]. The result also generalizes Lemma 3.7. Note that the original result in [68] is more general,which involves a logarithmic term,and is on the unit ball of C. Here is presented a simplified version on the unit disk. We don’t need all the cases, but we include all the cases here since this result is such an elementary estimation which is useful in many situations.

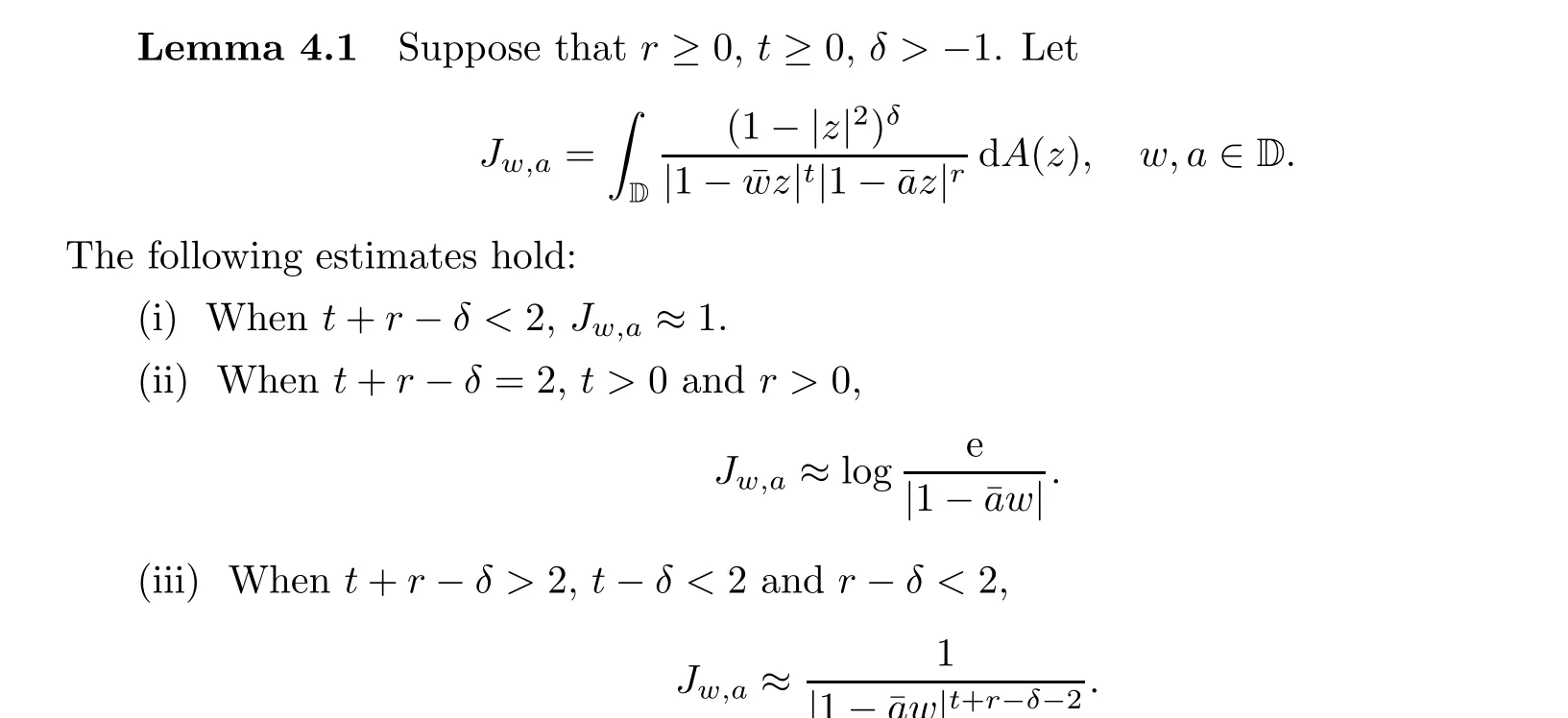
5 Bloch Stretch

By Proposition 2.5, we know that F(p,q,s) = Bfor s ＞1. By its definition, Bis characterized as the class of f whose derivatives satisfy the radial growth condition

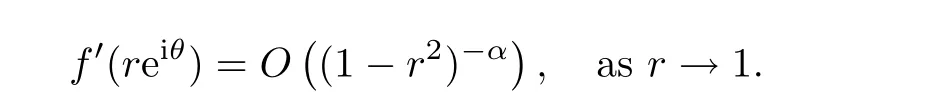
For 0 ≤s ≤1, the situation is more complicated, however we can describe the radial growth of the derivatives of functions in F(p,q,s) for 0 ≤s ≤1 with aid of the α-Bloch spaces. In [71],the author introduced a concept called the Bloch stretch as follows:

Definition 5.1 Letting X be a space or a class of analytic functions, we define the Bloch stretch of X as

We also call constants α= sup{α : B⊆X} and β= inf{β : X ⊆B} the lower and upper bound of the Bloch stretch of X, respectively.

The Bloch stretch is an intrinsic property of a space of analytic functions. If two such spaces have different Bloch stretches, or if they have the same Bloch stretch but with different upper or lower bounds, then they are sure to be different spaces.

with the lower bound (q+s+1)/p and the upper bound (q+2)/p.

Proof (i) Let 0 ＜α ＜(q+s+1)/p, and let f ∈B. Then we have

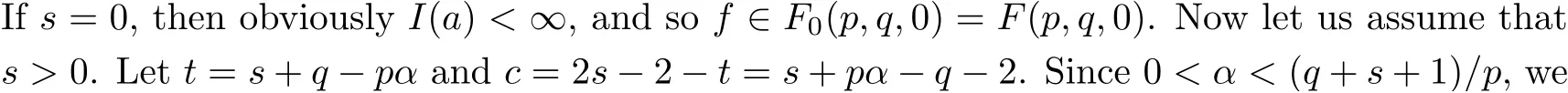
Thus f ∈F(p,q,s)for 0 ＜p ＜∞,-1 ＜q ＜∞,0 ≤s ＜1 with q+s ＞-1 and(q+2)/p ＞α.

Now, suppose that -2 ＜q ＜-1. If we denote that β = (q +2)/p, then β ＞αand pβ = q+2 ≤1. Thus 1/β ≥p. Since q+s = pβ+s-2 ＞-1, we know that β ＞(1-s)/p,or 1/β ＜p/(1-s). Hence, we may choose a number psuch that p ≤1/β ＜p＜p/(1-s).Denoting that q= pβ -2, we see from the above inequality that q＞-1. Since 1-(1-s)p/p ＞0, we may choose a number ssuch that 0 ＜s＜1-(1-s)p/p. By H¨older’s inequality, we get that

Since q=pβ-2 ＞-1, we get, by (5.2), that f ∈F(p,q,s). Thus, by (5.3) and (5.4), we get that f ∈F(p,q,s). Thus F(p,q,s)/⊆B.

(v) The result is a direct consequence of (i)-(iv). The proof is complete.□

6 α-M¨obius Invariance

Remark 6.7 For BMOA = F(2,0,1), since H= F(2,1,0), the result of Theorem 6.6 is well known (see, for example, [17, p. 15, Corollary 3]). Similarly, for B = F(2,0,2), since A= F(2,2,0), the result of Theorem 6.6 is also known (see [15]). For Q= F(2,0,s), the result corresponding to Theorem 6.6 has been proven in [11] and [12].

We have seen from Proposition 2.5 that all F(p,q,s) spaces are contained in some α-Bloch spaces. The next result provides an explanation for this phenomenon. It shows that the α-Bloch space is the maximum among α-M¨obius invariant spaces. We need the following concept:

Definition 6.8 A nonzero linear functional L on a Banach space X is said to be decent if there exist a constant M ＞0 and a compact subset K of D such that

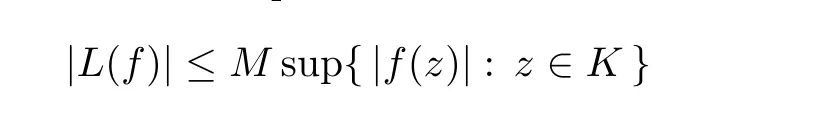
for all f ∈X.

Equivalently,L/=0 is decent if L extends to a continuous linear functional on H(D),which is the linear space of analytic functions on D (cf [50]).

Theorem 6.9 Let X ∈M(D), and let ρ be an α-M¨obius invariant semi-norm on X.If there exists a decent linear functional L on X that is continuous with respect to ρ, then X ⊆B. Moreover, there exists a constant A ＞0 such that ‖f‖≤Aρ(f) for all f ∈X.

For a proof of this,we refer to the proof of Theorem 4.7 in[71]. The above result generalizes the corresponding result for the Bloch space by Rubel and Timoney in [50].

The next result shows that for two positive numbers α/=β, a functional Banach space on D cannot be α-M¨obius invariant and β-M¨obius invariant simultaneously.

Theorem 6.10 Let 0 ＜α ＜β ＜∞, and let X be a functional Banach space on D. If X is β-M¨obius invariant, then X cannot be α-M¨obius invariant.

Proof Let X be a β-M¨obius invariant functional Banach space. Then, by definition,every point evaluation K: f →f(z) is a continuous linear functional. Obviously Kis a decent linear functional on X. By Theorem 6.9, we just need to prove that X /⊆B.

Denote the semi-norm of X by ρ. Suppose, on the contrary, that X ⊆B. Let I : X →Bbe the inclusion mapping. Then I(X) ⊆B. Let {f} ⊂X be a sequence such that ρ(f-f) →0 and ‖I(f)-g‖→0 as n →0. Since X is a functional Banach space, the point evaluation is continuous. Thus, there is a constant K =K(z)＞0 such that

Since X is a functional Banach space on D, there is a non-constant function f ∈X. Thus f(z) /≡0. Without loss of generality, from the β-M¨obius invariance, we may assume that

for all f,g ∈X and φ ∈Aut(D), we say that 〈·,·〉 is a M¨obius invariant semi-inner product.

In[18],Bao and Zhu replaced the existence of“decent linear functionals”by a slightly more strict but much simpler condition that there exists a constant C ＞0 such that |f(0)|≤Cρ(f)for each f in the space. Under this condition, they proved the existence of the smallest α-M¨obius invariant space and the existence and uniqueness of α-M¨obius invariant semi-Hilbert space, and hence answered two open questions from [71].

Now we present the two main theorems from [18].

7 Closure of F(p,q,s) in α-Bloch Spaces

A long-standing open question in the theory of function spaces has been how to characterize the closure of Hin the Bloch space B. While the problem is still open,Peter Jones successfully characterized the closure of BMOA in B. The solution is an easy consequence of a formula for the distance from a Bloch function to BMOA.

where C is a constant independent of a. Therefore, quantity (D) is bounded by a multiple of quantity (C). The proof is complete.□

From Theorem 7.1 we immediately obtain the following corollaries:

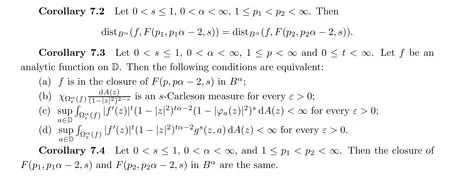
8 Riemann-Stieltjes and Multiplication Operators on F(p,q,s) Spaces

In this section we characterize nonnegative Borel measures μ such that the embedding from F(p,q,s)to a certain tent-type space is bounded or compact. The results will be applied to get characterizations for the bounded and compact Riemann-Stieltjes operators and the pointwise multiplication operators between F(p,q,s) spaces. All the results in this section come from[44]. The proofs are too complicated to be included in this short survey, so we refer to [44] for proofs of all theorems in this section.

8.1 Tent-type spaces and logarithmic Carleson measures

The (p,s)-logarithmic Carleson measures and vanishing (p,s)-logarithmic Carleson measures were introduced by the author in 2003 in[72]. Note that the(vanishing)(0,s)-logarithmic Carleson measures are just (vanishing) s-Carleson measures. We will denote by LCMthe class of all (p,s)-logarithmic Carleson measures, and denote that

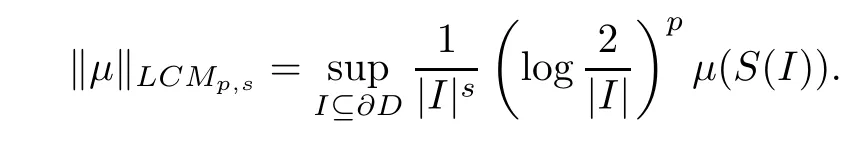
8.2 Bounded and compact embedding from F(p,pα-2,s) to T∞p,s(μ)

Theorem 8.5 Let α ＞1, s ＞0, and p ＞0 with s+pα ＞1, and let μ be a nonnegative Borel measure on D. Let γ =s+p(α-1). If 0 ＜p ≤1, or p ＞1 with γ ＞1, or 1 ＜p ≤2 with γ =1, then

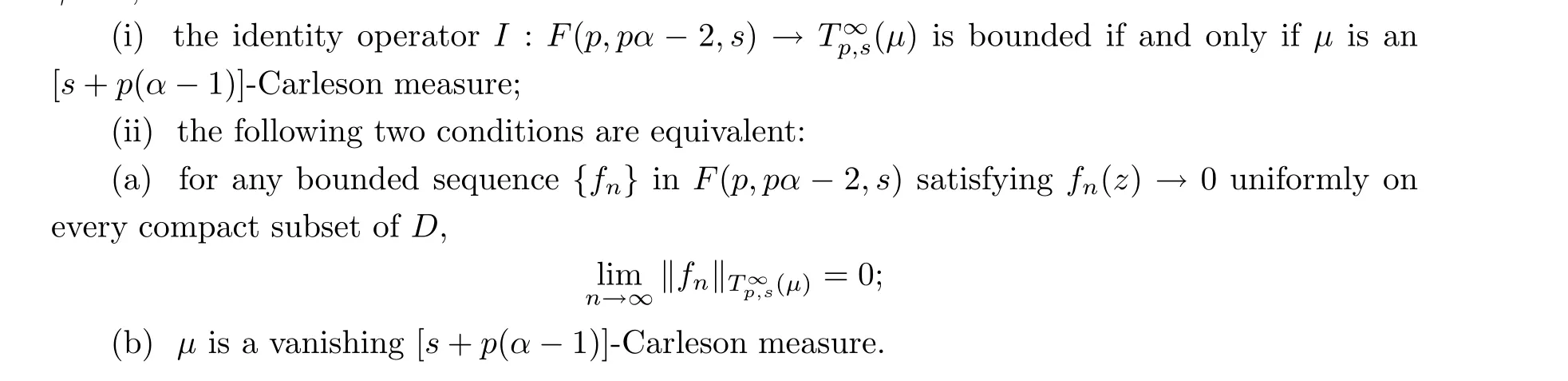
8.3 Riemann-Stieltjes operators on F(p,q,s) spaces

The operators Jwere first used by Pommerenke in 1977 in[47]to characterize BMOA functions.Pommerenke observed in [47] that Jis bounded on the Hardy space Hif and only if g ∈BMOA. These operators were first systematically studied by Aleman and Siskakis in 1995 in [5], who showed that Jis bounded on the Hardy space H(1 ≤p ＜∞) if and only if g ∈BMOA. Aleman and Siskakis studied these operators on weighted Bergman spaces in 1997 in [6], Siskakis and the author characterized the boundedness of Jon BMOA in [51]. Aleman and Cima characterized the boundedness of Jbetween different Hardy spaces in 2001 in [4].Hu [35-37] and Xiao [59, 60] studied these operators for various spaces in the setting of the unit ball. Later on, many other mathematicians studied these operators on various function spaces. An important special case of the operator Jis when g(z)=-log(1-z); in this case,Jis called the Ces`aro operator. To state our result, we need the following concept:

Definition 8.6 For 0 ＜p ＜∞, -2 ＜q ＜∞, 0 ≤s ＜∞such that q + s ＞-1,the logarithmic F(p,q,s) space F(p,q,s) is defined as the space of analytic functions f on D satisfying

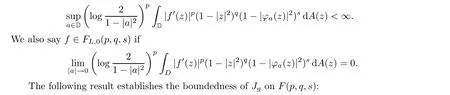
Theorem 8.7 Let α ＞0, s ＞0 and p ＞0 satisfy s+pα ＞1. Then we have the following results:

(i) As 0 ＜α ＜1, Jis bounded on F(p,pα-2,s) if and only if g ∈F(p,pα-2,s).

(ii) As α=1, Jis bounded on F(p,p-2,s) if and only if g ∈F(p,p-2,s).

(iii) Let α ＞1 and γ = s+p(α-1). For the cases 0 ＜p ≤1, or p ＞1 and γ ＞1, or 1 ＜p ≤2 and γ =1,we have that Jis bounded on F(p,pα-2,s)if and only if g ∈F(p,p-2,γ).

Remark 8.8 When p=2, α=1 and s=1, from Section 2, it is known that F(2,0,1)=BMOA, which is the space of analytic functions of bounded mean oscillation. In this case, the above result was first proved by Siskakis and the author in[51]. When p=2,α=1,0 ＜s ＜1,we know that F(p,pα-2,s) = Q. In this case, the result was first proved by Xiao in [61].Note also that in the case where α ＞1 and γ = s+p(α-1) ＞1, by Theorem 2.3, we know that F(p,p-2,γ)=B, which is the Bloch space.

For compactness, we have the following result:

Theorem 8.9 Let α ＞0, s ＞0 and p ＞0 satisfy s+pα ＞1. Then we have the following results:

(i) As 0 ＜α ＜1, Jis compact on F(p,pα-2,s) if and only if g ∈F(p,pα-2,s).

(ii) Jis compact on F(p,p-2,s) if and only if g ∈F(p,p-2,s).

(iii) Let α ＞1 and γ =s+p(α-1). For the cases 0 ＜p ≤1,or p ＞1 and γ ＞1,or 1 ＜p ≤2 and γ =1, we have that Jis compact on F(p,pα-2,s) if and only if g ∈F(p,p-2,γ).

8.4 Pointwise multiplication operators on F(p,q,s) spaces

Let X be an F-space of analytic functions, and let M(X)denote the space of all pointwise multipliers on X, that is,

Let Mdenote the pointwise multiplication operator defined by Mf =fg. Because the Closed Graph Theorem is still available for F-spaces (see [22, Chapter II]), we see that g ∈M(X) if and only if Mis bounded on X. For the little-oh case, we denote that

Theorem 8.10 Let α ＞0,s ＞0 and p ＞0 satisfy s+pα ＞1. Then we have the following results:

(i) If 0 ＜α ＜1, then M(F(p,pα-2,s))=F(p,pα-2,s).

(ii) If α=1, then M(F(p,p-2,s))=H∩F(p,p-2,s).(iii) Let α ＞1 and γ =s+p(α-1). Then,

(a) if 0 ＜p ≤1, M(F(p,pα-2,s))=F(p,p-2,γ);

(b) if p ＞1 and γ ＞1, M(F(p,pα-2,s))=H∩B =H;

(c) if 1 ＜p ≤2 and γ =1, M(F(p,pα-2,s))=F(p,p-2,γ)∩H.

Remark 8.11 When p=2, α=1 and s=1, we have F(2,0,1)= BMOA. For this case the above result was first obtained by Stegenga in [52] (see also [41] and [72]). When p = 2,α = 1, 0 ＜s ＜1, we know that F(2,0,s) = Q. For this case the result was first proved by Pau and Pel´aez in [43].

The next result shows that M(F(p,pα-2,s)) is always trivial.

Theorem 8.12 Let α ＞0, s ＞0 and p ＞0 satisfy s+pα ＞1. Then

9 Some Other Results and Comments

In this section we list some other recent results on F(p,q,s) spaces.

9.1 BMOAαp spaces

Among F(p,q,s) spaces, there is a special class which may be of some particular interest.

Definition 9.1 Let 0 ＜p ＜∞and 0 ＜α ＜∞. We define

Definition 9.3 Let g be an analytic function on D, and let X and Y be two spaces of analytic functions. We say that g is a pointwise multiplier from X into Y if gf ∈Y for any f ∈X. The space of all pointwise multipliers from the space X into the space Y will be denoted by M(X,Y).

The next result is from [73]. It gives us one example that the behavior of BMOAspaces is indeed similar to the behavior of the α-Bloch space B.

9.2 Preduals of F(p,q,s) spaces

where the infimum is taken over all such representations of f.

In what follows,if X is a Banach space, the notation Bdenotes the closed unit ball of X,Xdenotes the the dual space of X, and co denotes the compact-open topology. If X and Y are Banach spaces,the notation X ～=Y means that X is isomorphic to Y. The following result,which is one of the main results in [38], shows that R(p,q,s) is the dual space of F(p,q,s):

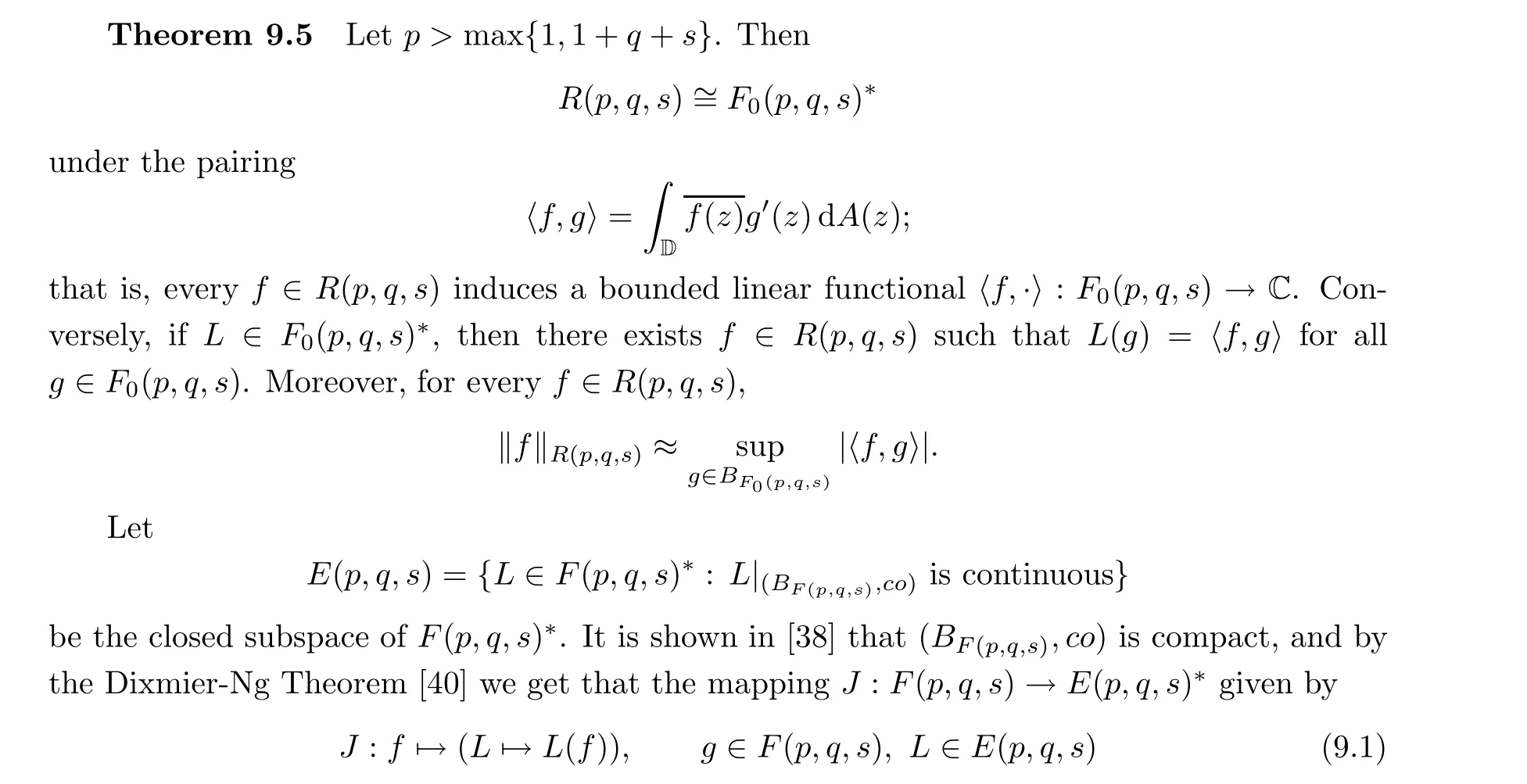
is an isometric isomorphism. Hence, we get the following result, which is originally from [38]:

Theorem 9.6 The E(p,q,s) space is a Banach space and J : F(p,q,s) →E(p,q,s)given by (9.1) is an isometric isomorphism.

From this, the authors in [38] get their second main result:Theorem 9.7 Let q ≥0 and p ＞1+q+s. Then

(i) E(p,q,s) is the unique isometric predual of F(p,q,s);

(ii) E(p,q,s)～=R(p,q,s);

(iii) F(p,q,s)is isometrically isomorphic to F(p,q,s).

9.3 F(p,q,s)-domains

Let f be a univalent function in H(D). For a Banach space X ⊆H(D), we say that Ω = f(D) is an X-domain whenever log f∈X. For a univalent function f on D, we denote the Schwarzian derivative of f by

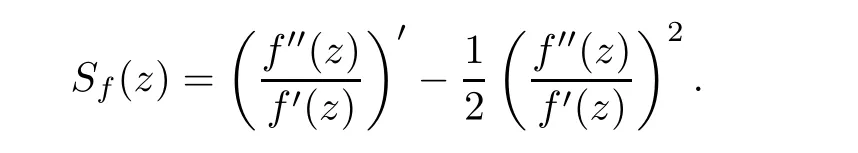
Zorboska studied the F(p,q,s) and F(p,q,s) domains, and obtained the following characterizations in [79]:

Theorem 9.8 Let f be univalent on D, 1 ≤p ＜∞, -2 ＜q ＜∞, 0 ≤s ＜∞such that q +s ＞-1. Let Ω = f(D), and let ∂Ω be a Jordan curve. If q +2 = p, then Ω is an F(p,q,s)-domain if and only if dμ(z) = |S(z)|(1-|z|)dA(z) is an s-Carleson measure. If q+2 ＜p, then Ω is an F(p,q,s)-domain if and only if log f∈Band dμ(z)is an s-Carleson measure.

Theorem 9.9 Let f be univalent on D, 1 ≤p ＜∞, -2 ＜q ＜∞, 0 ≤s ＜∞such that q + s ＞-1. Let Ω = f(D), and let ∂Ω be a Jordan curve. If q +2 ≤p, then Ω is an F(p,q,s)-domain if and only if dμ(z) = |S(z)|(1-|z|)dA(z) is a vanishing s-Carleson measure.

9.4 QK(p,q) spaces

In the definition of F(p,q,s)spaces, we used the weight function tfor the term g(z,a). In[55], Wulan and Zhou replace tby a more general weight function K(t)to get a generalization of F(p,q,s) spaces called Q(p,q) spaces. Here is the definition:

Definition 9.10 Let K : [0,∞) →[0,∞) be a right-continuous and nonincreasing function. For 0 ＜p ＜∞and -2 ＜q ＜∞, the space Q(p,q) consists of f ∈H(D) such that

It is known that Q(p,q) is a Banach space for p ≥1 under the norm |f(0)|+‖f‖,and that Q(p,q) is a closed subspace of Q(p,q). Obviously, as K(t) = t, 0 ≤s ＜∞, we get that Q(p,q)=F(p,q,s) and Q(p,q)=F(p,q,s).

Some basic properties of Q(p,q) spaces have been studied in [55] and [56], and subsequently by some other authors. Here we list a few results on Q(p,q) spaces from [55] and[56].

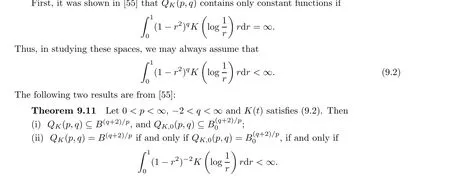
The next result shows that the weight function K can be chosen to be bounded.

Theorem 9.12 Let 0 ＜p ＜∞, -2 ＜q ＜∞. Assume that K(t) satisfies (9.2) and K(1)＞0. Let K(r)=inf(K(r),K(1)). Then Q(p,q)=Q(p,q).

In [56], the authors gave characterizations for Q(p,q) spaces using higher derivatives. In particular,they provided a characterization of Q(p,q)spaces with Carleson measures involving higher derivatives. To state their result, we need some more restrictions on the weight function K.

In what follows, we assume that K is differentiable and satisfies K(2t) ≈K(t), and also that K(0)=0 (otherwise, Q(p,q)=F(p,q,0)). For 0 ＜s ＜∞, let

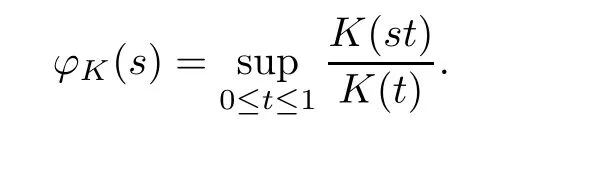
see Section 1.2 in [77] for the details about φ.

For some other work on F(p,q,s) spaces on the unit ball of C, see, for example, [46,58, 66, 69]. As a related generalization, in [42], Ouyang, Yang and the author generalized Q=F(2,0,s) spaces from the unit disk to the unit ball Bof Cusing the M¨obius invariant gradient and M¨obius invariant Green’s functions on B.

10 Concluding Remarks

With 25 years of development since the introduction of F(p,q,s)spaces in[71]in 1996,the theory of F(p,q,s) spaces has become a very active field of research. Below is a list of a few other recent results on F(p,q,s) spaces.

· In[28],Feng,Huo and Tang introduced F(p,p-2,s)-Teichm¨uller spaces,which generalize some known spaces such as the BMO-Teichm¨uller space and the Weil-Petersson Teichm¨uller space. They also investigated the Schwarzian derivative model and the pre-logarithmic model of F(p,p-2,s)-Teichm¨uller spaces.

· El-Sayed and Omran in [24] and Miss Paredes, Res´endis Ocampo and Tovar S´anchez in [39] generalized F(p,q,s) spaces on the unit disk in the complex plane to F(p,q,s) spaces of quaternion-valued functions in the unit ball in Rand studied the basic properties of these spaces.

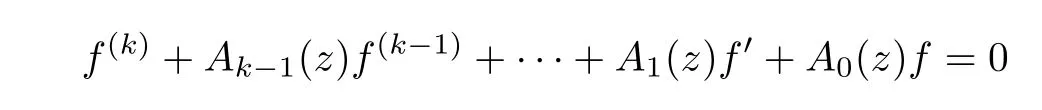
· In [62], Li-Peng Xiao studied the differential equation with coefficients Aanalytic on the unit disk,and gave some sufficient conditions such that the solutions belong to the F(p,q,s) space.

· In[57],Wynn applied the theory of F(p,q,s)spaces to provide a solution to the weighted Weiss conjecture in the linear system theory and the control theory.

· In [65], Yuan and Tong studied relations between analytic Campanato spaces and F(p,q,s) spaces.

· In a series papers, [31-33] and [34], Hu and Li studied the spaces of analytic functions in the unit ball of Cwhose primitives are in F(p,q,s) spaces.

· In [25], Engliˇs introduced a very general class of function spaces on the unit disk which are invariant under weighted M¨obius actions; these include the spaces of analytic functions whose primitives are in F(2,q,s) spaces.

This short survey only touches on a tiny part of the research on F(p,q,s) spaces. For example, we did not include the vast amount of research on operators such as composition operators, weighted composition operators and some integral operators on F(p,q,s) spaces.It is clear that the theory of F(p,q,s) spaces has connections with many different fields of mathematics,and provides a proper stage for studying the behavior of various operators. There are still many unsolved problems regarding F(p,q,s) spaces. For example, it is still not known what conditions characterize bounded and compact composition operators on F(p,q,s) spaces or between F(p,q,s)spaces. Hopefully this short survey will help to entice new researchers into this exciting and rich field of research.