商代的算术运算和甲骨文上的数字排列
2021-02-23吴文俊
吴文俊






在商代,人们所知道的数目仅是一个有限的自然数集合,还没有涉及分数或小数.由此推知:当时不可能有除法运算.商代人肯定会加法运算,因为这是人类最容易掌握的一种算术运算.在商代也可能出现过乘法运算,实际上算术的乘法运算只是一种相同的数目的连续相加,这种加法人们无疑会经常遇到,久而久之乘法便产生了,人们就不必再将相同的数目连续相加了.进行乘法运算的关键是运用九九乘法表.有了九九乘法表,个位数与个位数的乘积念一次九九乘法口诀就出来了;将两位数以上的数相乘还要借助少量的加法运算来辅助.但是,目前我们还没有在甲骨文中找到九九乘法表,不过不能断定其一定不存在.至于减法运算,只能在被减数大于减数时才能进行.我们推测,数目很小的减法在商代可能存在,不过不一定能普遍施行.
根据个别的例子,大体可以窥见一点商代的算术运算.在一片甲骨上有4列数字,即50、30、20和15,每个数字出现3次(图1).释文可排列为如下的形式:
五十犬五十羊五十豚
三十犬三十羊三十豚
二十犬二十羊二十豚
十五犬十五羊十五豚
由于骨片的上端残缺,五十()只有一个比较清楚,因此人们有不同的猜测,李俨、李迪等认为最上面的一列文字为五十犬、五十羊、五十豚,而陈梦家则不承认这列文字.实际上,经仔细观察可发现,最上面一列文字是存在的.
这个实例中包含着一些数学规律,可能也用到了运算,李俨作了如下解释:
50-30=4×5=22×5,
30-20=2×5=21×5,
20-15=1×5=20×5.
他说这些结果中含有等比数列,而原来的4个数目都是5的倍数.上面的解释不仅涉及了减法和乘法运算,而且还含有等比数列的概念,但这种可能性不大,商代不可能形成等比数列的概念.我们认为这4列数字可能通过加法和乘法运算获得,是否有减法难以确定.
甲骨文中数字的排列都有一定的规律,根据这些规律可以窥见商代人已经掌握或可能掌握的数学知识.连续排列的数目字绝大多数到九为止,少数的到十(),超过十的极为罕见.下面举例加以说明.我们按甲骨文原来的排列位置进行摘录,仅仅把甲骨文字改为现代汉字.
第一类:若干个连续自然数的按顺序排列.
例1. 在同一片龟甲上有由一到六按顺序排列,且都是竖排的数目字.
例2.次序由右到左(即右小左大)横排排列的数目字:五、四、三、二、一.
例3.由上到下逆序排列的数目字:六、五、四,但是骨片上下端均残缺,估计还有字,至少往下还有三、二、一,上面就不好推测了.
至于由右到左(即右大左小)的横排的数目字的例子相当多,这里不另列举.
第二类:某个自然数的重复排列.
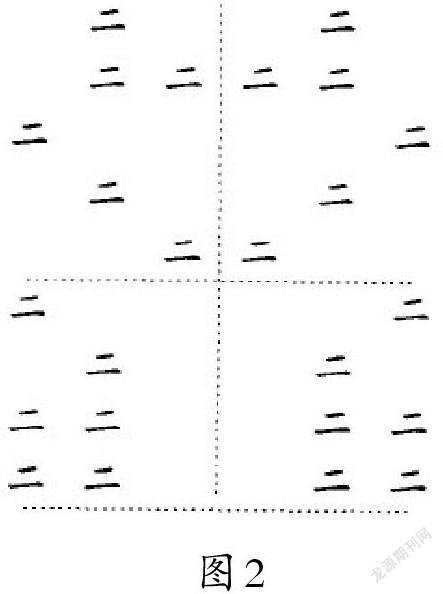
例1.反复出现同一个自然数.在一片甲骨上“二”字出现了24次,因骨片残缺,可能整个骨片上的“二”字比24个要多些.这24个“二”字可分为四组,用横、竖线隔开,每组6个,如图2.这种排列有什么意义,目前还不清楚.但未发现有类似情况的其他数字.
例2.在一片甲骨的残片上包含有“一”“二”“三”和“五”4个数字,中间的上端有2个横排的“一”,其左下和右下各有一列竖向排列的 “二”,左列“二”的左侧为两行“三”,右列“二”的右侧为“五”,实际上可能是两行“五”,因甲骨残损而看不见了.
例3.分段重复排列.有的连写几个“二”,接着几个“三”,每两个字中间有较大距离:有的连写几个”一”,似乎是把旁边的文字分为几段.
第三类:左右对称排列.这类的例子很多.
例1.在一片残甲骨上找到由一到十的数字40个,还有些地方模糊不清或有残损.根据整个排列我们补上8个数字,用方框圈起(如图3).如果从中间上下画一条直线,恰好分成左右对称的两部分.
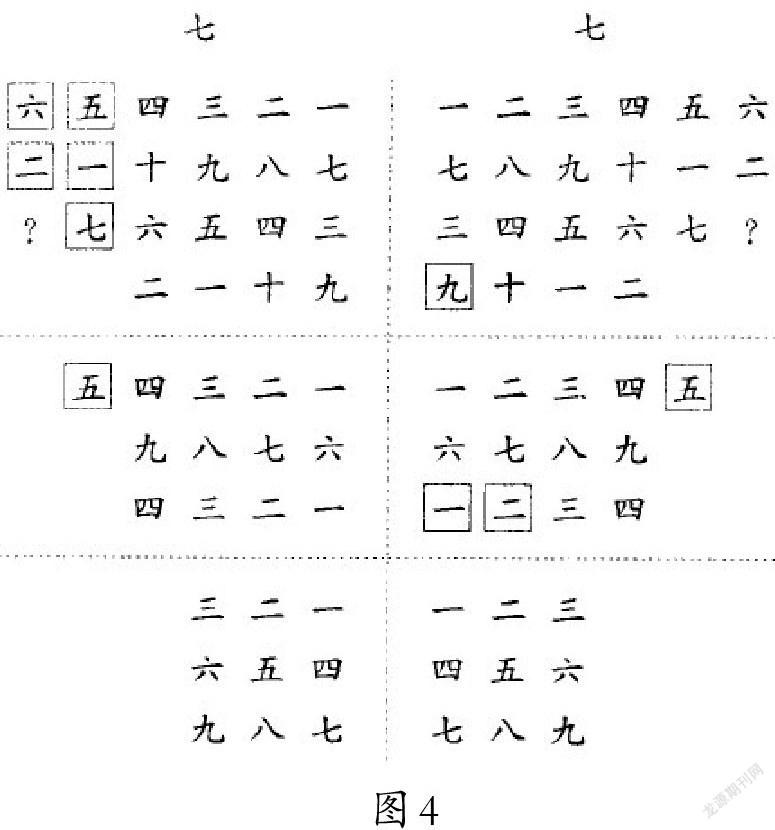
例2.在另一片甲骨上还有更复杂的左右对称排列的数字,如果说上面的例子可以分为上下两段的话,那么这个例子就可以分为三段,每段都左右对称.当然其中也有些残破或不清之处,补上相应的数字,排列如图4所示.
还有许多对称的例子,这里不再列举.但是值得我们深思的是,商代人对数字的排列有较多的认识,且达到了较高的水平.
第四类:奇偶分开排列.
一片龟甲的正面有28个数字、上下分为4列、每列7个数字.用十字线将其分成4个组,上两组共有6个数字,下两组共有8个数字.这样,每组的竖列、每列是奇或是偶很清楚地呈现出来,无一混乱,且下面两组左右对称(图5).
例2.在一片龟甲的下半截有18个自然数,分为4列排列.中间2列都是奇数,外边的2列都是偶数,它们左右对称.但右边微残,如二、八所在位置看不清,这很容易补上(图6).
例3.还有一种特殊的奇偶排列,如图7.其上部奇偶排列出现了交叉的情形,连线即可看出.其下部出现了循环的现象,即十下接二、四,九下有一、三.因有殘损,下面是否还有数字无法判断.根据这种循环现象,可知商代人使用的数字一般到十为止,过十则再从一开始.
第五类:前9个自然数的分三段排列.分段排列的情况在甲骨文中比较常见,例如,一个骨片上有由左(小)到右(大)分两段的横排数字,即一、二、三、四、五、六;七、八、九、十,下面又出现一、二、三、四,如图8.
例1.另一片甲骨的下半部也呈三段排列,上半部是两行自然数(图9).
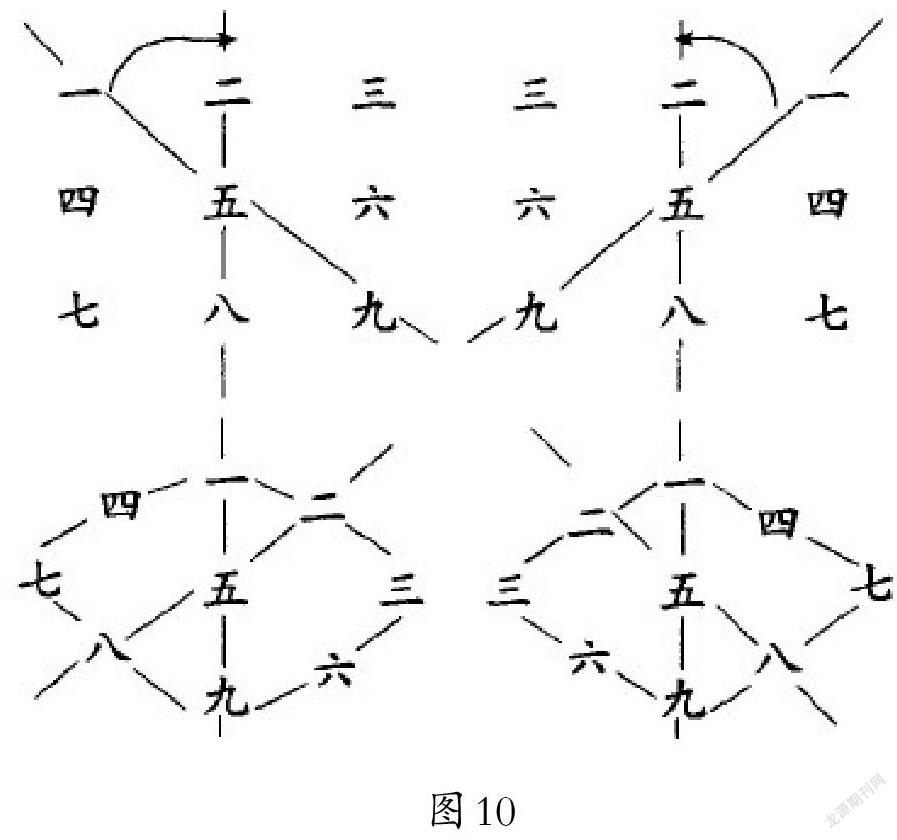
例2.独立的三段排列,也能在甲骨文中找到,有一个是由右(小)到左(大)排列的.这类排列有一个共同的特点,就是把它们左旋或右旋45°(如图10),便得到了3阶不完全的纵横图,如果把一与九、三与七分别对调就得到了现代意义下的幻方,因此有人已提出纵横图起源于甲骨文的论点.尽管这个论点还有待于进一步探讨,但是后人从这里得到启发而形成三阶纵横图也是有可能的.
由上述各种情况来看,商代人对自然数已经相当熟悉,而且掌握了一些规律,他们对数学排列的对称性似乎有所偏爱,在很多龟甲上都左右对称地排列着两列自然数.奇偶分列也是商代人很重视的事.
——摘自《中国数学史大系·第一卷》
