罐车爬壁射流清洗小车力学特性分析

翁 隽 吴志刚

江苏省特种设备安全监督检验研究院南通分院 江苏南通 226011

1 分析背景

罐体内部清洗是罐车检验前必不可少的程序,传统的人工清洗方式存在效率低、能耗高、污染大、劳动强度大等缺点,并且安全事故多。高压水射流清洗技术作为一种高效环保的清洗手段,在国内外已被广泛关注,发展迅速[1-2]。

爬壁机器人是高压水射流清洗设备的执行机构,作为极限作业机器人的一个重要分支,在桥梁与隧道检测、高层建筑清洗、反恐侦查等领域具有广阔的应用前景[3-5]。目前大部分爬壁射流机器人的研究主要集中于船舶除锈领域[6-7],多数船舶除锈爬壁机器人采用履带行走[8],力学分析的倾角范围在0°～90°之间,并不适用于在封闭罐体内进行360°全方位行走的罐车爬壁射流清洗小车。

笔者建立罐车爬壁射流清洗小车的力学模型,对不同工况进行分析,为电磁铁、电机、减速机的选型提供理论依据。

2 结构与工作原理

爬壁射流清洗小车主要由车体、驱动机构、俯仰曳引机构、喷刷机构、电磁吸附机构等组成。驱动机构采用四台交流伺服电机提供动力,可以通过控制各个伺服电机的转速和转向来实现清洗小车加减速与转向。清洗小车工作时,电磁吸附机构中周向对称安装的四个电磁铁为清洗小车提供足够的磁吸附力,保障车体附壁行走。四台伺服电机驱动清洗小车行走、攀爬和转向,俯仰曳引机构牵引清洗小车完成壁面转换。喷嘴喷射出高压水射流,水射流的反冲力为钢丝刷旋转提供动力,最终实现清洗小车在运动中边冲边刷的清洗作业。爬壁射流清洗小车结构如图1所示。

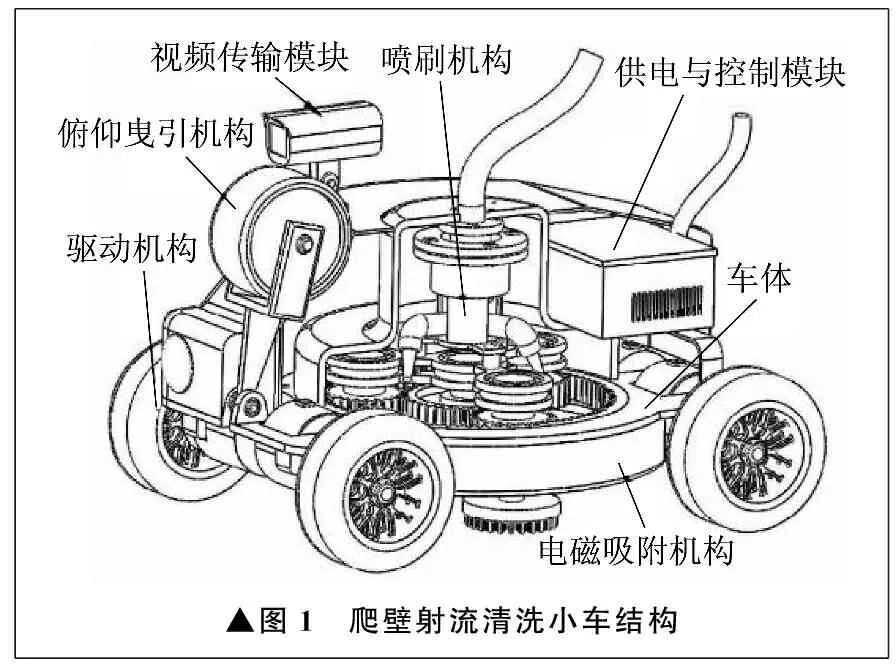
▲图1 爬壁射流清洗小车结构

3 静力学分析

爬壁射流清洗小车在罐体壁面吸附时的纵向位姿静力学模型如图2所示,横向位姿静力学模型如图3所示。图2、图3中,G为清洗小车重力,Fq为射流反冲力,Fci为单个电磁铁的吸附力,Ns为壁面对钢丝刷的支持力,fs为壁面对钢丝刷的静摩擦力,Ni为单个车轮所受的壁面支持力,fi为单个车轮所受的壁面静摩擦力,θ为壁面倾角,L1为清洗小车质心与壁面间的距离,L2为前后车轮间的距离,L3为清洗小车质心与后车轮间的距离,L4为后磁铁与后车轮间的距离,L5为前磁铁与后车轮间的距离,L6为左右车轮间的距离,L7为清洗小车质心与右车轮间的距离,L8为右磁铁与右车轮间的距离,L9为左磁铁与右车轮间的距离。

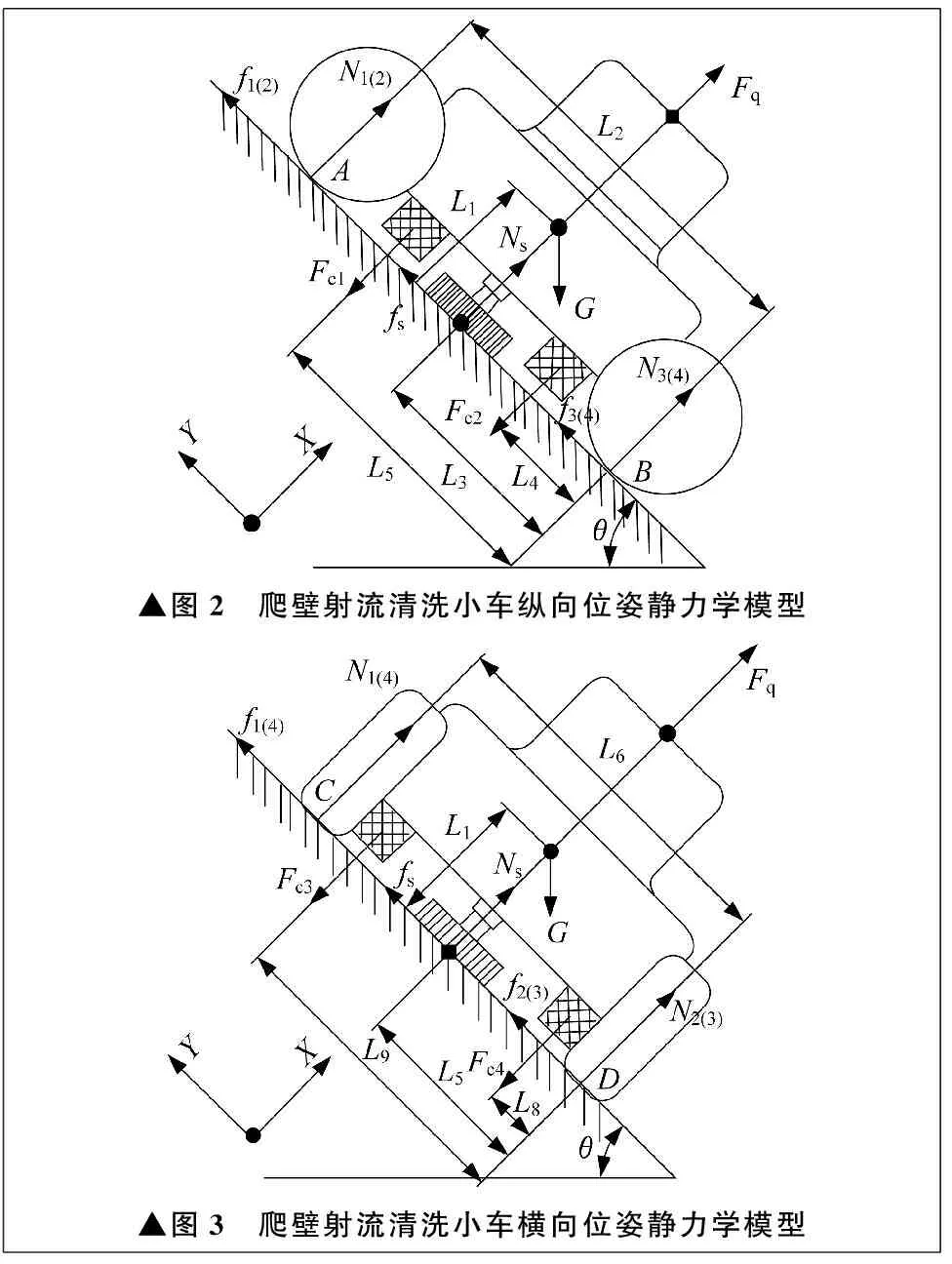
▲图2 爬壁射流清洗小车纵向位姿静力学模型▲图3 爬壁射流清洗小车横向位姿静力学模型

3.1 沿壁面下滑

爬壁射流清洗小车吸附在罐体内壁时,有沿壁面下滑的趋势,需要车体与罐体内壁接触部分提供足够大的静摩擦力来防止清洗小车的相对滑移。

当壁面倾角θ为0°～180°时,清洗小车纵向位姿可靠吸附的静力平衡方程为:

(1)

(2)

为避免清洗小车沿壁面下滑,需满足:

(3)

fi=μ1Ni

(4)

fs=μ2Ns

(5)

式中:μ1为壁面与车轮间的静摩擦因数,μ1=0.6;μ2为壁面与钢刷间的静摩擦因数,μ2=0.3。

由于四个电磁铁的规格型号相同,认为各自所产生的磁吸附力也相同,根据式(1)、式(2)、式(3),为保证清洗小车对罐体壁面无相对滑移,单个电磁铁吸附力应满足:

(6)

同理,当壁面倾角θ为180°～360°时,为保证清洗小车对罐体壁面无相对滑移,单个电磁铁吸附力应满足:

(7)

3.2 纵向倾覆

爬壁射流清洗小车在壁面上纵向吸附时,可能会绕B点发生纵向倾覆脱落,为保证清洗小车不发生纵向倾覆,需要电磁吸附力来提供抗倾覆力矩。

当壁面倾角θ为0°～180°时,清洗小车绕B点的力矩平衡方程为:

GL3cosθ+(Fc1+Fc2)L5+(Fc3+Fc4)L4

-(N1+N2)L2-GL1sinθ-N3L3-FqL3=0

(8)

为避免清洗小车绕B点发生纵向倾覆脱落,需要满足:

N1>0

(9)

N2>0

(10)

可得单个电磁铁吸附力应满足:

(11)

同理,当壁面倾角θ为180°～360°时,为避免清洗小车绕A点发生纵向倾覆脱落,单个电磁铁吸附力应满足:

(12)

3.3 横向翻转

爬壁射流清洗小车在壁面上横向吸附时,可能会绕D点发生横向翻转脱落,为保证清洗小车不发生横向翻转,需要电磁吸附力来提供抗翻转力矩。

当壁面倾角θ为0°～180°时,清洗小车绕D点的力矩平衡方程为:

GL7cosθ+(Fc1+Fc4)L9+(Fc2+Fc3)L8

-(N1+N4)L2-GL1sinθ-NsL7-FqL7=0

(13)

为避免清洗小车绕D点发生横向翻转脱落,需要满足:

N1≥0

(14)

N4≥0

(15)

可得单个电磁铁吸附力应满足:

(16)

同理,当壁面倾角θ为180°～360°时,为避免清洗小车绕C点发生横向翻转脱落,单个电磁铁吸附力应满足:

(17)

3.4 数值模拟

将各计算参数代入式(6)、式(7)、式(11)、式(12)、式(16)、式(17),得到静态最小吸附力模拟曲线,如图4所示。

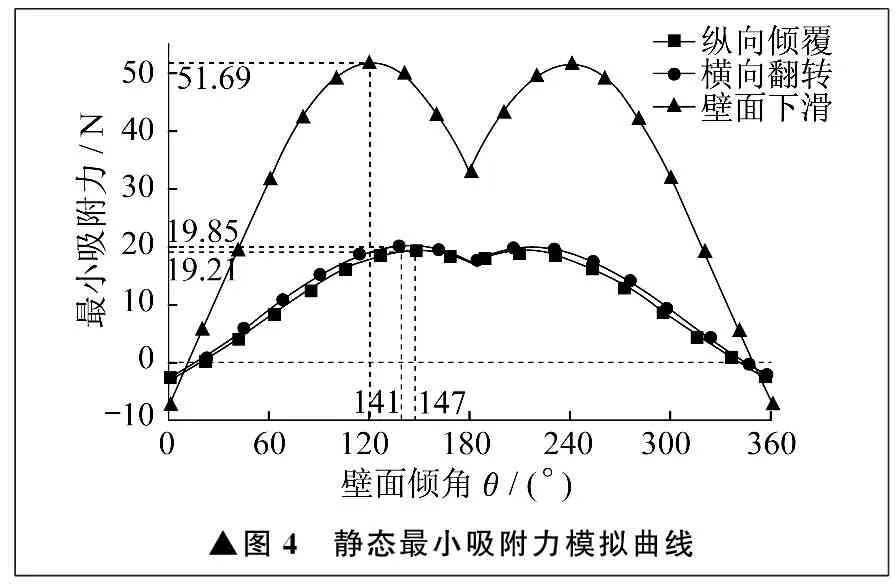
▲图4 静态最小吸附力模拟曲线

对于横向翻转,最小吸附力峰值在壁面倾角为141°时得到,为19.85 N。对于纵向倾覆,最小吸附力峰值在壁面倾角为147°时得到,为19.21 N。对于壁面下滑,最小吸附力峰值在壁面倾角为120°时得到,约为51.69 N。对比发现,防止清洗小车沿壁面下滑所需的最小吸附力远大于其余两种失稳形式,因此清洗小车最容易发生的失稳形式为沿壁面下滑。为防止沿壁面下滑失稳形式的发生,每一个电磁铁至少要能提供51.69 N的电磁吸附力。

4 动力学分析

4.1 直线行驶

爬壁射流清洗小车在执行单圈清洗时,直线行驶动力学模型如图5所示。

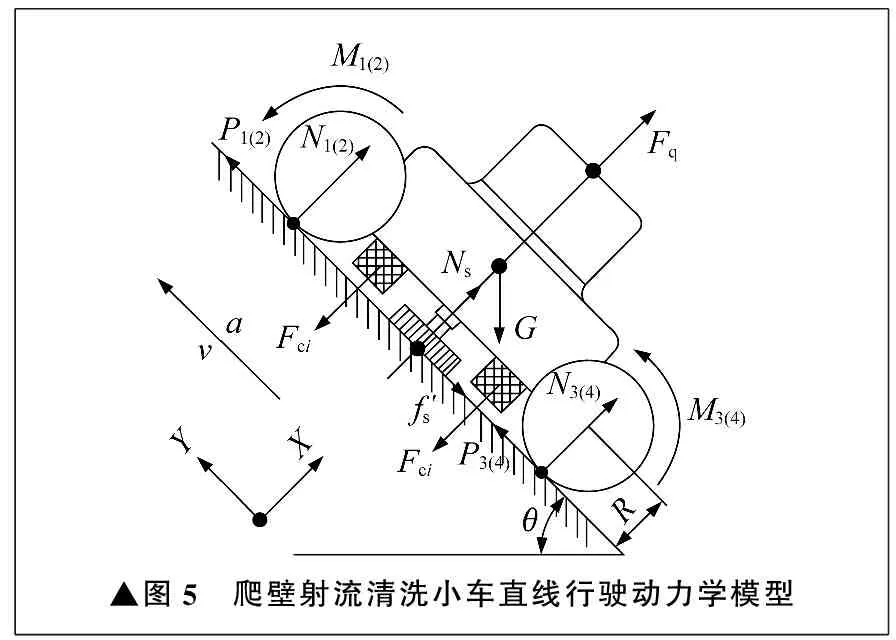
(19)

图5中,Mi为单个车轮的驱动力矩,Pi为单个车轮所受的壁面牵引力,f′s为壁面与钢丝刷的滑动摩擦力,R为车轮半径,a为清洗小车行驶加速度。

根据动力学模型,当壁面倾角θ为0°～360°时,清洗小车的驱动平衡方程为:

(18)

式中:m为清洗小车质量。

为保证清洗小车稳定驱动行驶,单个车轮需满足:

Mi-PiR-Jiαi≥0

(20)

式中:Ji为单个车轮转动惯量;αi为单个车轮角加速度。

清洗小车的四个车轮采用同种电机驱动,可以认为Pi相等,Mi相等,则单个车轮的驱动力矩应满足:

(21)

式中:μ3为壁面与钢丝刷的动摩擦因数,μ3=0.5。

4.2 差速转向

爬壁射流清洗小车在罐体壁面上转向靠左右两侧车轮的速度差来实现,对清洗小车进行原地差速转向动力学建模,如图6所示。图6中f′i为壁面与单个车轮之间的滑动摩擦力,d为钢丝刷旋转直径。

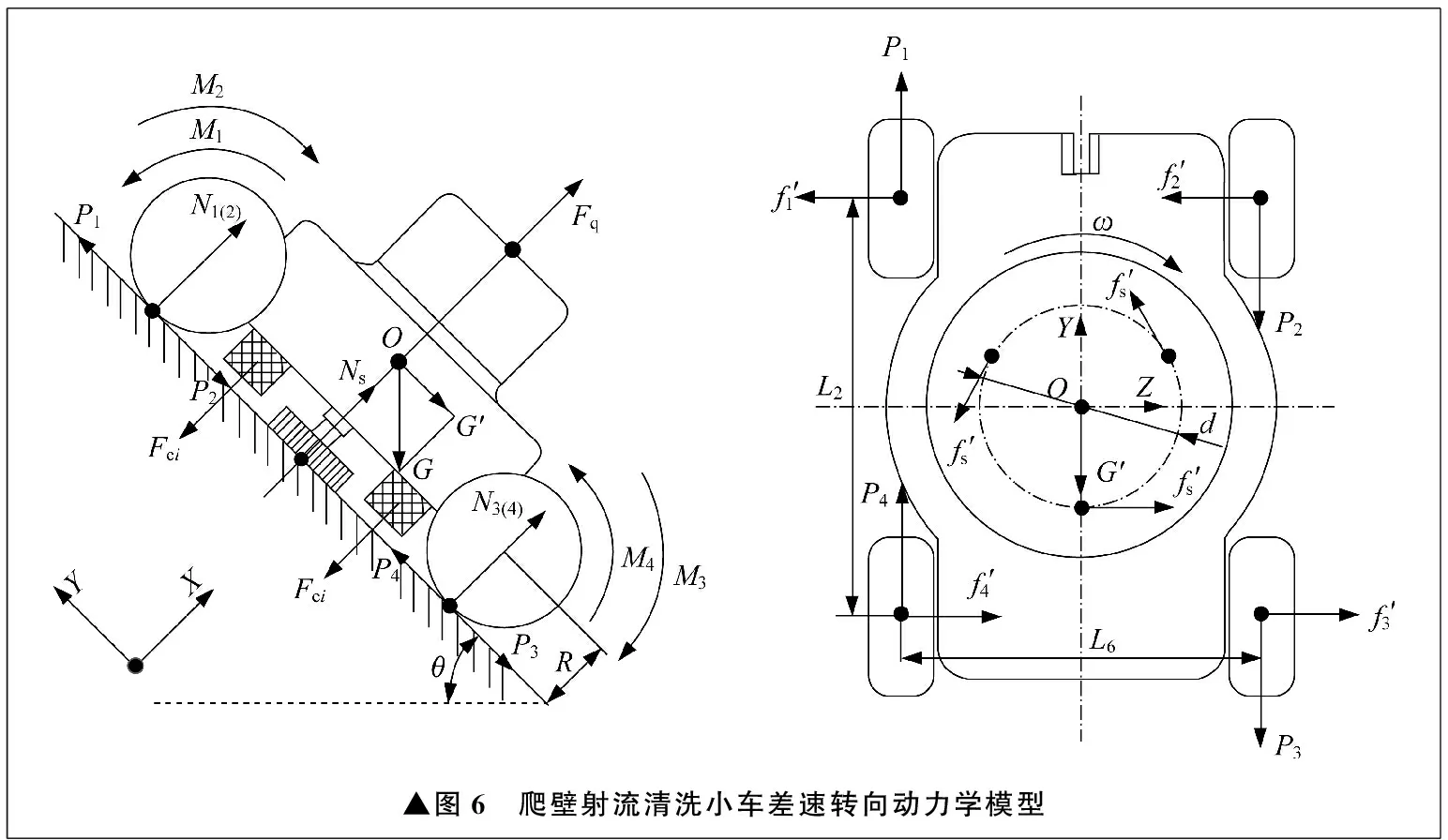
▲图6 爬壁射流清洗小车差速转向动力学模型

假设清洗小车的转向过程为匀速转动,根据动力学模型,当壁面倾角θ为0°～180°时,清洗小车的转向平衡方程为:

(22)

P1-P2-P3+P4-Gsinθ=0

(23)

(24)

为保证清洗小车匀速平稳转向,单个车轮需满足:

M1-P1R≥0

(25)

单个车轮所需驱动力矩应满足:

(26)

式中:μ4为壁面与车轮橡胶的动摩擦因数,μ4=0.8。

同理,当壁面倾角θ为180°～360°时,为保证清洗小车匀速平稳转向,单个车轮所需驱动力矩应满足:

(27)

4.3 数值模拟

将各计算参数代入式(21)、式(26)、式(27),得到匀速直线行驶与差速转向的动态驱动力矩模拟曲线,如图7所示。

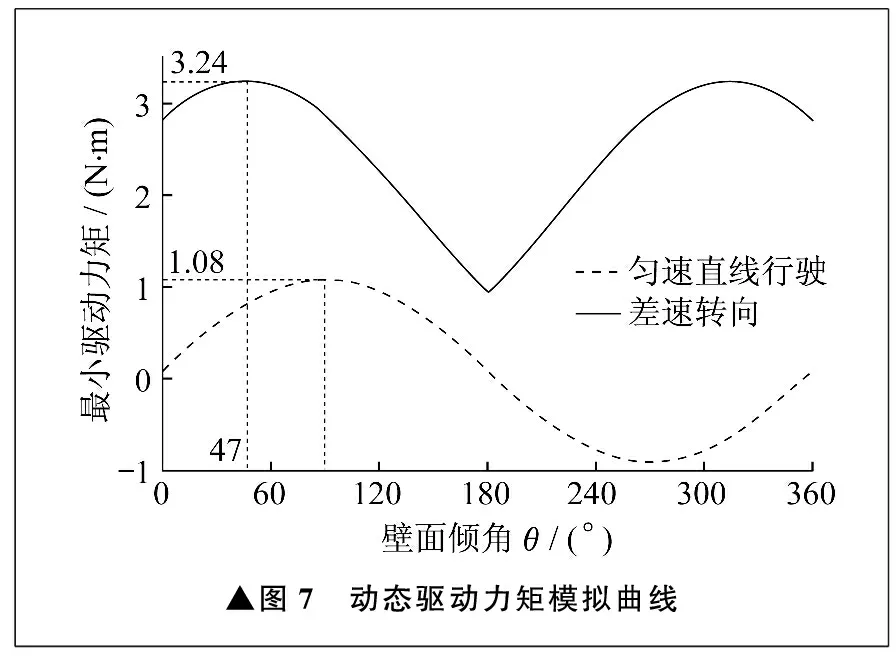
▲图7 动态驱动力矩模拟曲线

由图7可以看出,在任意壁面倾角下,差速转向所需的最小驱动力矩都远大于匀速直线行驶,因此清洗小车在进行罐体内壁清洗的行走过程中,最容易发生的失稳形式是差速转向受阻,或者因驱动力矩不足导致转向不到位及转向偏移等情况。因此,为确保清洗小车在清洗过程中平稳运行,每个车轮需提供的驱动力矩至少为3.24 N·m。

5 结束语

笔者对爬壁射流清洗小车在罐体壁面的清洗工作进行分析,针对清洗小车静态受力和动态驱动,对清洗小车进行了静力学和动力学建模,推导电磁铁吸附力保证清洗小车不下滑、不倾覆、不翻转,以及驱动力矩保证清洗小车平稳直行、转向五个理论公式,并且得到了清洗小车的吸附最易失稳形式和行驶最易失稳形式,为清洗小车电磁铁、驱动电机及相应减速机的选择提供了依据,也为罐车爬壁射流清洗设备的力学分析提供了参考。

分析得出,清洗小车最易发生的吸附失稳形式为沿壁面下滑,最易发生的行驶失稳形式为差速转向,保证清洗小车稳定可靠运行的最小电磁吸附力为51.69 N,最小驱动力矩为3.24 N·m。